涡轮叶型冷热态转换在液体火箭发动机中的应用
任 众,许开富,韩 飞
(西安航天动力研究所,陕西 西安 710100)
0 引言
对于闭式循环的液体火箭发动机系统,主涡轮的效率、流通能力、轴向力对发动机性能及工作可靠性影响巨大。因此,在设计阶段对涡轮气动参数的精确控制至关重要[1-3]。同时涡轮部件工作在高温、高压、高转速的条件下,叶片载荷大,温度分布复杂,导致涡轮部件发生显著的变形,而这些变形又会对涡轮气动性能参数产生影响[4]。
在以往的液体火箭发动机涡轮设计中,一般是根据气动性能指标设计出满足要求的叶片,而将该叶片直接作为加工状态(冷态)叶片,不考虑叶片工作过程变形对性能的影响,见图1中的传统设计流程[2-3]。从严格意义上讲,设计者根据气动性能指标设计出的叶片应为工作状态(热态)的叶片,即工作变形后的叶片。如果变形对气动参数影响不大,则可以按照传统方法直接将热态叶片当做冷态叶片进行加工;反之,则需要在设计阶段进行变形预补偿,将热态工作叶片转化为冷态加工叶片,使叶片工作变形后达到设计者要求的型面精度,从而气动参数得到精确控制,见图1中的考虑变形补偿的设计流程[5-6]。
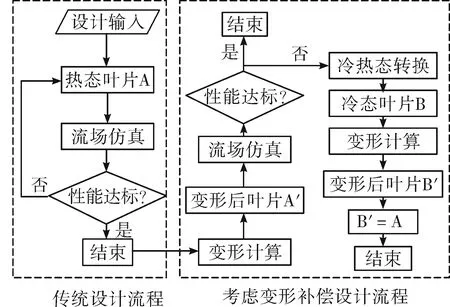
图1 涡轮气动设计流程Fig.1 Aerodynamic design flowchart of turbine
本文提出了一种涡轮叶片冷热态转换的方法,并以某发动机主涡轮为研究对象,首先对比了叶片变形对气动性能的影响,然后采用该方法针对气动、离心、热载荷作用下叶片变形进行预补偿,将工作状态(热态)叶型转化加工状态(冷态)叶型,为涡轮设计提供依据。
1 叶片变形预补偿方法
由图1中涡轮叶片变形补偿流程可知,该流程分为补偿必要性分析与冷热态转换两部分。完成热态叶片设计后,首先需要进行补偿必要性分析,即对比叶片变形前后对主要设计指标的影响,如果影响可以忽略,则不必进行补偿设计,如果影响较大,则必须进行变形补偿,将设计的热态叶型转换为冷态加工叶型。下文主要针对该流程中的两个关键环节进行方法介绍,即变形后叶片快速重构方法和叶片冷热态转换方法。
1.1 叶片快速重构方法
在补偿必要性分析及冷热态转换的迭代过程中,均要求对变形后的涡轮叶片进行再造型,整个变形补偿流程中该过程将多次出现,本部分介绍一种快速造型方法。
涡轮叶片的三维造型示意图见图2。由图可知,叶片型面根据NURBUS曲面构造原理由M个截面积叠得到,每个叶片截面为N个控制点生成的样条曲线,叶片型面由造型点Pij精确控制的。而通过有限元计算只能得到的叶片表面各网格节点Nk的变形量,由图3可知,叶片表面有限元节点的排列是无序的。因此,对变形后叶片的三维再造型,必须将有限元节点Nk上的变形量大小及方向投影到造型点Pij上,得到造型点变形后的精确位置。
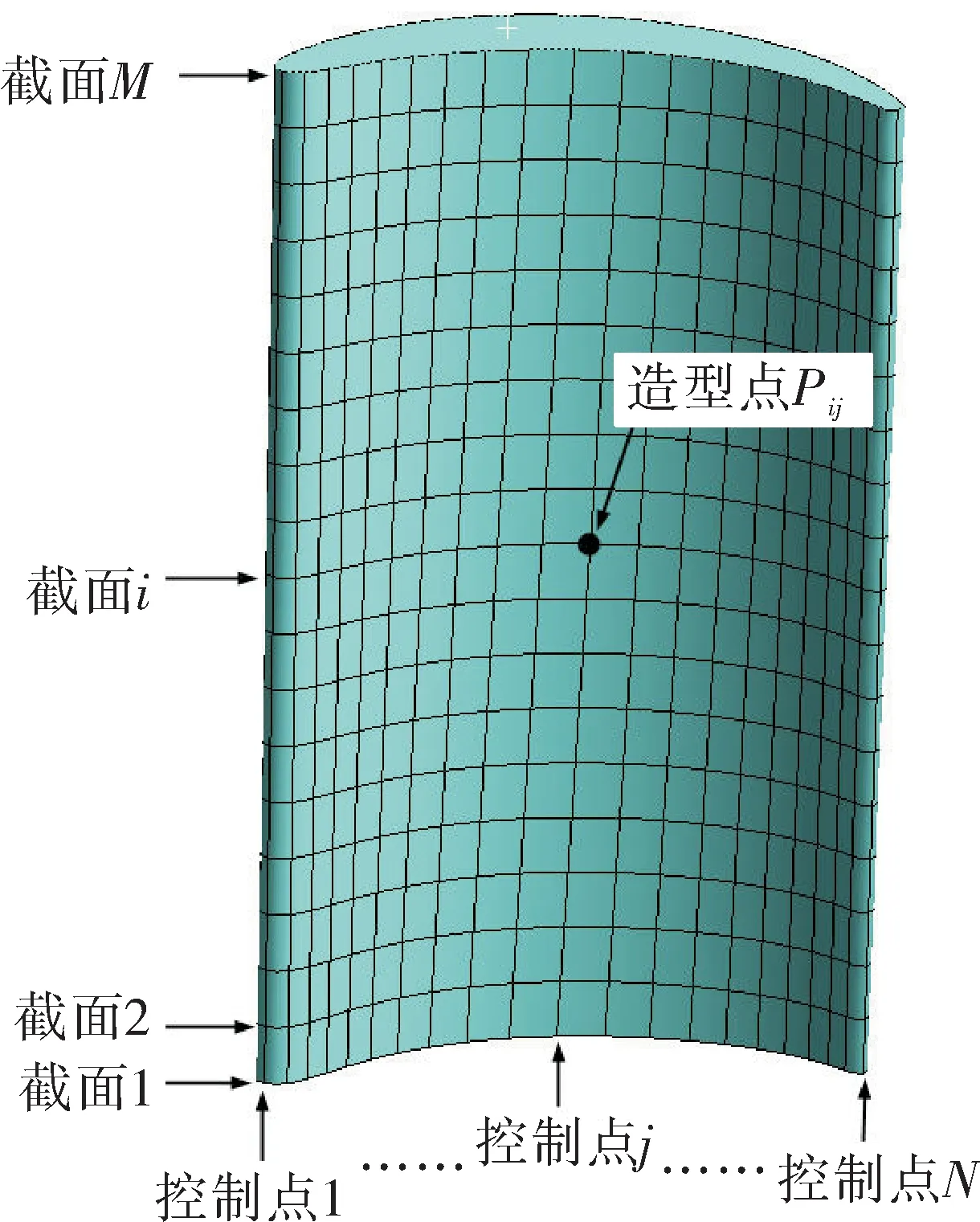
图2 叶片三维造型示意图Fig.2 3-D structure model of blade

图3 叶片有限元节点Fig.3 Finite element nodes of blade
通过BP神经网络对有限元计算结果进行处理,得到叶片造型点处的变形量大小及方向。由于有限元网格节点的数据量大,相比于微元法、三角剖分法、三维插值等方法,该方法具有简单可靠、精度高、收敛速度快等优点[7]。
设给定N个样本(Xk,Yk) (k=1,2,…,N),由BP神经网络得到的输出Ok为:
Ok=f(W(l)Xk)
(1)
式中:W(l)为连接第l层与第l+1层之间各神经元节点的权值矩阵;f(·)为神经元传递函数,一般使用可微的Sigmoid型函数。
计算网络输出Ok与理想输出Yk之间的误差为:
(2)
通过BP神经网络对变形后的叶片再生成过程如下:
1)提取有限元计算结果中各网格节点的坐标值Nk(xk,yk,zk)及变形量ΔNk(Δxk,Δyk,Δzk)。其中前者作为网络输入样本Xk,后者作为网络理想输出样本Yk,样本数为有限元网格节点数;
2)通过迭代调整各层之间的权值矩阵W(l),使误差E满足精度要求,从而得到叶片表面节点坐标位置与变形量的映射关系;
3)将造型点的坐标值Pij(xij,yij,zij)作为输入样本,经过上一步已训练好的BP神经网络计算,得到的网络输出即为各造型点的变形量ΔPij(Δxij,Δyij,Δzij),从而得到变形后的造型点Pij′(xij+Δxij,yij+Δyij,zij+Δzij)的坐标;
4)对变形后叶片不同截面型线上的点进行光顺处理,再进行曲面重构生成叶型。
1.2 叶片冷热态转换迭代方法
本文采用的叶片冷热态转换方法见图4。由图可知,在每一轮迭代中均需完成流固耦合变形计算及叶片重构。对转换后的叶片要进行误差分析,以确定是否达到位置精度,本文采用冷态叶片变形后与热态叶片造型点之间的最大距离来描述位置偏差,即:
(3)
式中误差精度ε一般根据叶片的加工情况取加工精度。如果在该误差精度下性能仍无法满足要求,则认为性能偏差是由加工精度引起的,而非冷热态叶型偏差引起。
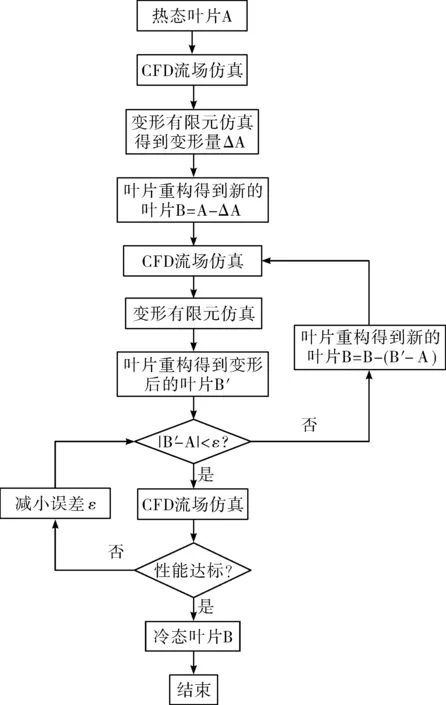
图4 叶片冷热态转换流程Fig.4 Cold and hot state conversion flowchart of turbine blade
2 叶片变形预补偿算例
2.1 研究对象及建模
以某单级反力式涡轮为研究对象,其三维模型见图5。静叶与进气壳体为一体结构,涡轮盘为带围带的整体结构。静叶与动叶均为扭曲叶型,采用10截面积叠生成,每个截面由160个造型点控制,并在前尾缘处加密控制。
涡轮的流场计算模型及边界见图6。由图可知,采用单通道模型进行计算,计算域由静叶通道、动叶通道、涡轮盘腔及轮盘顶部泄漏腔四部分组成,为了获得涡轮盘两侧及围带的压力、温度分布,因此加入了涡轮盘腔与顶部泄露腔两个计算域。
对计算域均采用六面体结构网格进行划分,壁面处进行附面层加密处理,控制壁面的最大y+值在200内,网格单元数188.8万。利用商用软件CFX完成涡轮流场仿真,静叶入口设置为总压入口,动叶出口设置为静压出口,对称面设置为周期边界,静子域与转子域之间采用Stage级交接面,其余壁面按照绝热壁处理,湍流模型设置为SST,采用高阶差分格式对方程进行离散求解。
由有限元计算模型及边界图可知,采用二十节点六面体网格进行网格划分,静子模型节点数5.4万,涡轮盘节点数2.8万。在静子出口法兰面约束轴向与周向自由度,在涡轮盘进口端面约束轴向自由度,内孔花键处约束周向自由度。分别对涡轮静子部件及涡轮盘在综合载荷作用下进行有限元变形计算,将插值得到的表面压力直接作为气动载荷,而表面稳态温度场先进行导热计算,将得到的体温度作为热载荷。

图5 有限元计算模型及边界Fig.5 Calculation model and border of finite element
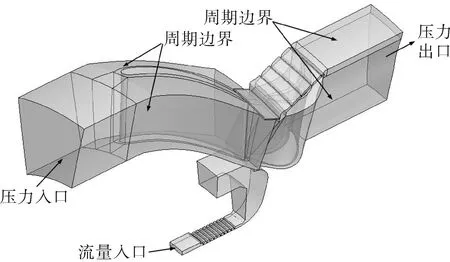
图6 流场计算模型及边界Fig.6 Calculation model and border of flow field
本部分针对气动、离心、热载荷作用下叶片变形进行预补偿,将工作状态叶型转化加工状态叶型。对该过程做了如下简化及假设:
1)只研究叶片变形,忽略子午面及动叶顶部泄漏间隙的变形影响;
2)计算及转换过程中保证叶片根部的轴向相对位置不变,即静叶轴向变形为相对于根部截面尾缘点,动叶轴向变形为相对于根部截面前缘点;
3)在冷热态转换的迭代求解过程中不进行CFD流场仿真,由于该涡轮叶片的变形主要由热载荷引起,而叶片变形较小,可以忽略变形对温度场的影响。
2.2 叶片变性前后性能分析
本部分对热态叶片进行设计工况的流固耦合变形仿真,并对变形后的叶片进行重构,对比变性前后涡轮的主要气动性能参数,以此进行补偿必要性分析。
计算得到的设计状态下涡轮叶片变形分布见图7,由图可知,静子叶片最大变形位于尾缘中部,大小为0.80 mm,占叶片宽度的1.45%。转子叶片最大变形量位于叶顶前缘,大小为1.91 mm,占叶片宽度的5.23%。
保持子午面、叶根轴向相对距离及动叶顶部间隙不变,对变形后的叶片重构,再进行一轮流场仿真,得到叶片变形前后涡轮性能对比,见表1。由表可知,变形后的涡轮效率略微降低,流量增加较大,导致涡轮功率与设计值存在偏差,涡轮泵的工作状态将偏离设计状态;同时变形后涡轮轴向力变化大,不利于涡轮泵轴向力平衡系统设计。因此,有必要对热态叶片进行变形预补偿,转化为冷态加工叶片,以精确控制涡轮流量及轴向力。

图7 涡轮叶片变形分布Fig.7 Deformation distribution of turbine blade
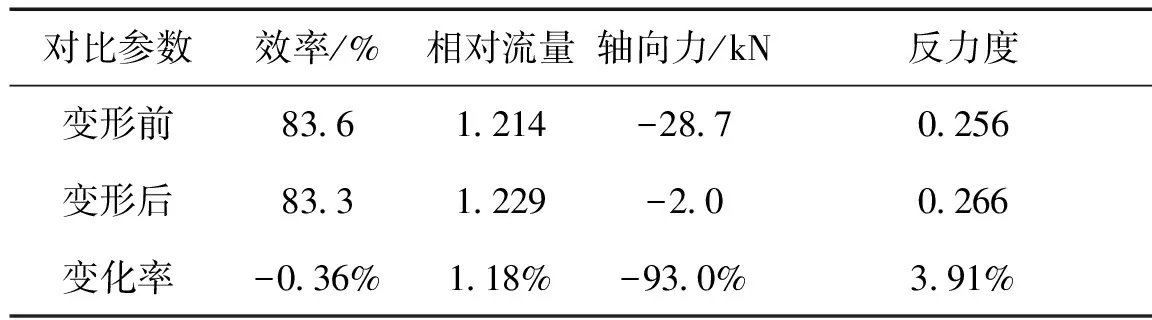
表1 叶片变形前后涡轮性能对比
注:轴向力正好指向涡轮出口。
2.3 叶片冷热态转换
针对设计出的热态叶片,按图4的方法进行有限元变形计算及叶型修正重构迭代,直到变换后的叶片满足位置精度。根据叶型的实际加工精度,本文的涡轮迭代位置偏差精度选取0.05 mm。共进行了三轮转换迭代,每一轮迭代后叶片间的位置偏差见表2。由表可知,第一轮迭代后,即直接将热态叶片减去变形量,得到位置误差已经控制在0.2 mm以内,经过三轮迭代,位置偏差已满足精度要求。
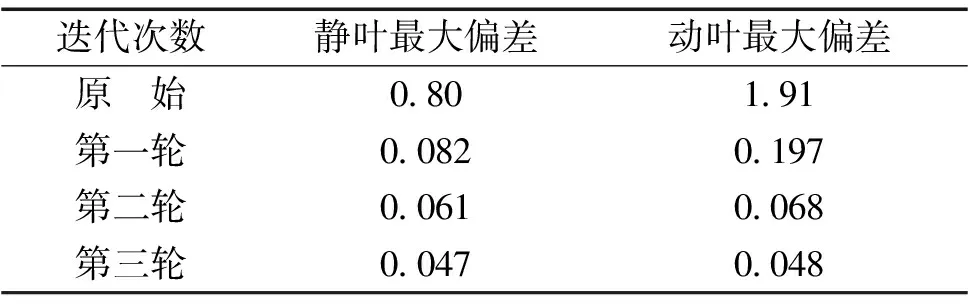
表2 各轮迭代叶片位置误差
经过变形预补偿后的冷态叶型与热态叶型对比见图8。由图可知,静叶的变形补偿量较小,而动叶的补偿量较大,主要由于涡轮盘上的温度梯度大,所引起的热变形较大。为了更精确的控制涡轮气动参数,应该按照图中的深色冷态叶型加工叶片。
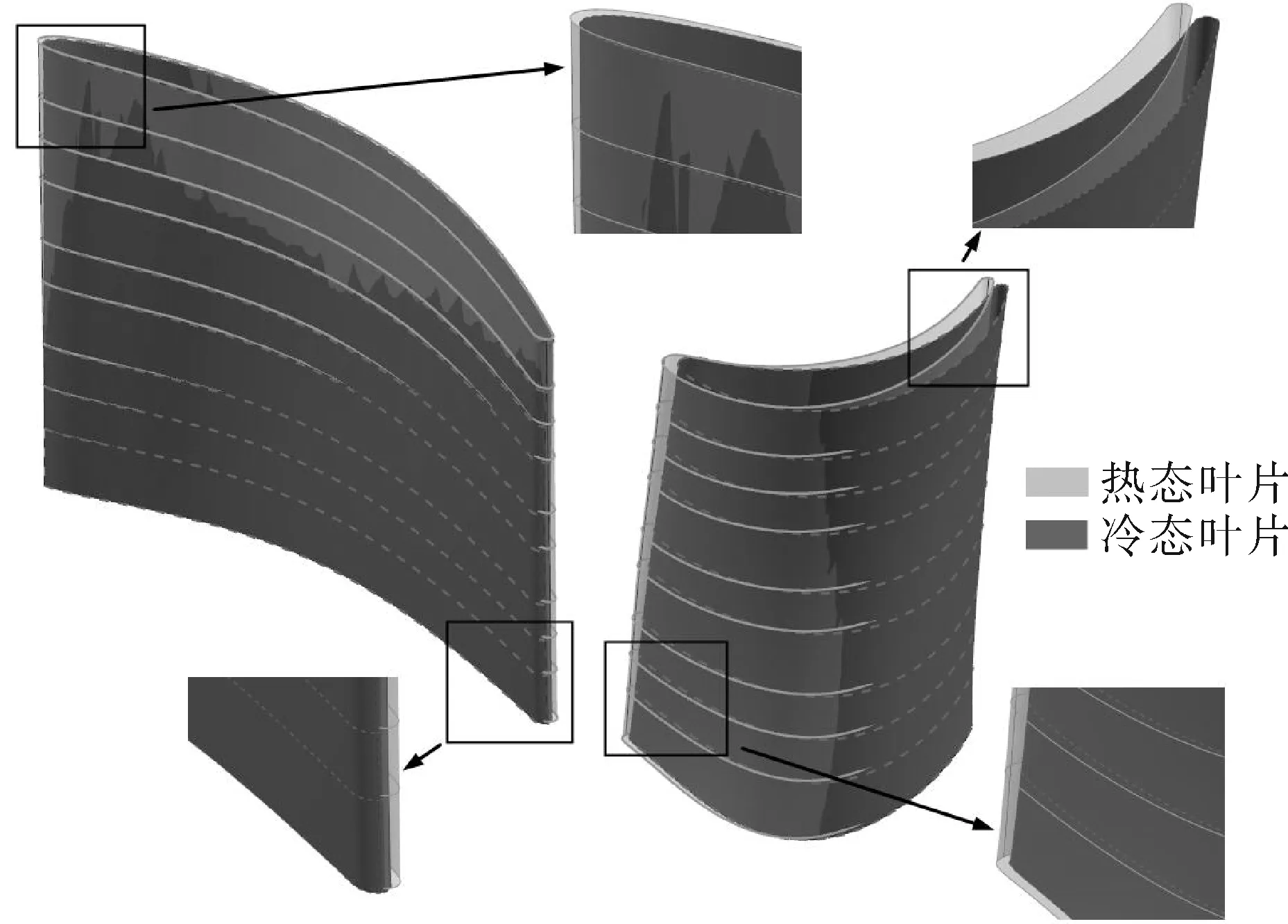
图8 冷热态叶型对比Fig.8 Comparison of cold and hot state blade profiles
3 结论
提出了一种涡轮叶片冷热态转换的方法,并以某涡轮为研究对象,针对气动、离心、热载荷作用下叶片变形进行预补偿。主要结论如下:
1)叶片变形补偿过程分为必要性分析及冷热转换两部分,该过程中叶型重构采用BP神经网络算法,冷热态叶型转换采用修正迭代的方法。结果表明,该方法可以使叶片的气动参数得到精确控制,可开展工程应用。
2)对于闭式循环的液体火箭发动机,涡轮叶片变形对效率、流量、轴向力等气动参数影响较大,有必要进行冷热态叶型转换。
3)本文的工作只针对叶片变形进行补偿,未考虑子午面及动叶顶部间隙的变形影响,其变形补偿方法类似,后续可进一步开展研究。
参考文献:
[1] 张贵田. 高压补燃液氧煤油发动机[M]. 北京:国防工业出版社,2005.
[2] 李斌,王晓峰,陈本森,等. 大叶顶间隙高效率火箭发动机涡轮设计[J]. 宇航学报,2009,30(2):695-698;
[3] 庄毓南,张国舟,刘中祥,等. 液体火箭发动机高效率反力式涡轮的设计[J]. 北京航空航天大学学报,1999,25(6):696-699.
[4] 王鹏,廖平,岳莉莉,等. 透平叶片在气热固耦合场下的热变形分析[J]. 机械科学与技术,2015,34(3):348-351;
[5] 王延荣,黄钟山,付志忠,等. 基于热态叶型的小轮毂比弯掠叶片结构保形设计与优化[J]. 航空动力学报,2015,30(10):2305-2311;
[6] 王鹏. 多能场作用下透平叶片的服役变形机理与设计补偿[D]. 长沙:中南大学,2014.
[7] 廖建国,张弛. 一种BP神经网络算法的改进模型[J].火力与指挥控制,2009,34(11):57-60.
[8] 徐楠,安莎,白东安,等. 上面级发动机小功率冲击式涡轮性能试验研究[J].火箭推进,2016,42(6):43-47.
XU Nan,AN Sha,BAI Dongan,et al. Performance test for low-power impact turbo of upper stage liquid rocket engine [J]. Journal of rocket propulsion,2016,42(6): 43-47.
[9] 窦唯,叶志明,闫宇龙. 涡轮泵叶轮/转子配合间隙对稳定性的影响[J].火箭推进,2016,42(4):26-34.
DOU Wei,YE Zhiming,YAN Yulong. Effect of tolerance clearance between turbine rotor and impeller in liquid-propellant rocket engine on stability [J]. Journal of rocket propulsion,2016,42(4): 26-34.

