覆盖阶梯电极的石英晶体圆板高频振动分析

于兰珍，吴荣兴，李晓东，郑东，邱耀

（1.宁波职业技术学院 建筑工程学院，浙江宁波，315800；2.宁波大学机械与力学学院，浙江宁波，315211）

0 引言

石英晶体谐振器作为频率控制元件在电子器件领域中有着广泛的应用[1]。其频率稳定性是器件设计人员首先需要考虑的问题，各种石英晶体谐振器的结构因素和环境因素都将对谐振器工作频率产生巨大影响[2]。Wang和Zhao分析了石英晶体矩形板的厚度剪切振动，并提出了石英晶片最佳长厚比的选取方法[3]。有限元法同样被用来分析石英晶体谐振器的各种结构效应[4]。

在实际产品设计过程中，都会尽量将厚度剪切振动的能量集中于石英晶体谐振器的中间，以避免过多的能量损耗[5]。本文设计了覆盖阶梯电极的石英晶体圆板模型，并以此分析了厚度剪切振动模态的振动特性，为覆盖阶梯电极的新型石英晶体谐振器的研制奠定了基础。

1 控制方程

厚度剪切振动是AT切石英晶体谐振器的工作模态，表现为关于圆板中线的反对称模态，可以由覆盖板上的金属电极激发[1]。为了更好地获得相应的能陷效应，阶梯电极如图1所示。厚度剪切振动位移表达式为[5]

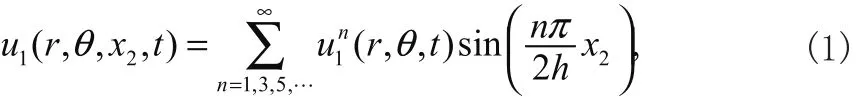
式中,h,r,θ,x和t分别是总位移、n阶厚度剪切振动2的位移、石英晶片的半板厚、半径、转角、厚度坐标和时间变量。当n=1时，厚度剪切振动为基频振动，当n＞1为高频振动[1]。

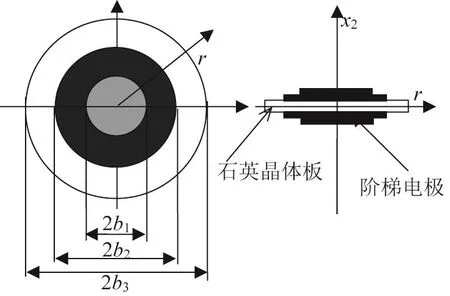
图1 覆盖阶梯电极的石英晶体圆板

未覆盖电极和覆盖电极的厚度剪切振动的控制方程分别为[5]

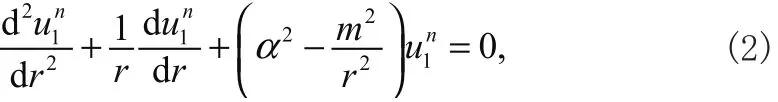
和

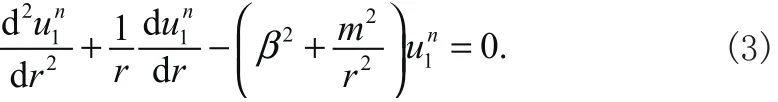
控制方程的参数如下[5]

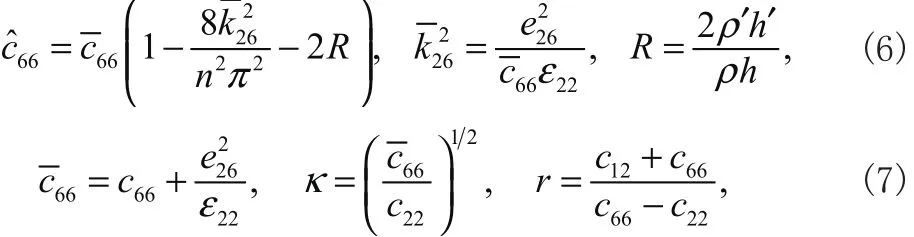
式 中 cpq(p ,q =1,2,3,4,5,6), eip(i =1,2,3), εij( j =1,2,3),ρ,2h′,ω和ρ′分别为AT切石英晶体的弹性常数、压电常数、介电常数、石英晶体密度、电极厚度、频率和电极密度。

针对频率方程(2)和(3)，可以假设解为

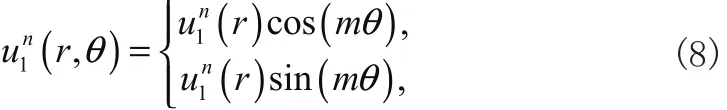
式中 m = 0 ,1,2,···。将 (8) 代入 (7)，可以得到

和

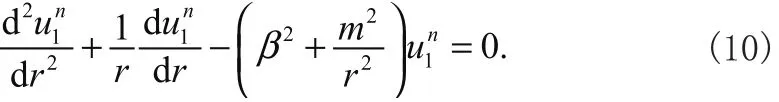
方程(9)和(10)的通解为

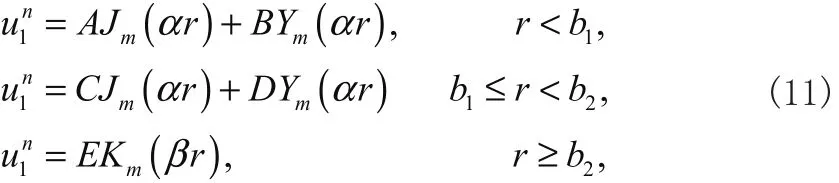
式中 A (B ,C,D,E)是振幅，Jm和 Ym分别为第一类和第二类贝塞尔函数。

对应于图1所示的边界条件，在不同覆盖电极厚度处的边界条件为位移和斜率连续，同时假定一定远处的位移为零，如下

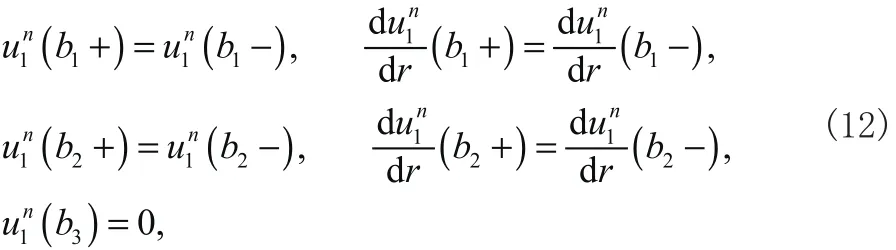
式 b3为一定远处的半径。将位移代入边界条件(12)，可以获得关于振幅 A (B ,C,D,E )的线性方程组，如果振幅存在非零解，其系数行列式的值必为零，可以获得频率ω的方程。

2 算例

这里考虑石英晶体材料为AT切石英晶体，覆盖金属电极为银，具体材料常数可见文献[6]。设定h=0.343915mm，b1=1 mm，b2=2 mm，b3=5 mm。可以绘制出覆盖阶梯电极的AT切石英晶体圆板的基频(n=1)厚度剪切振动的位移振动模态如图2所示。

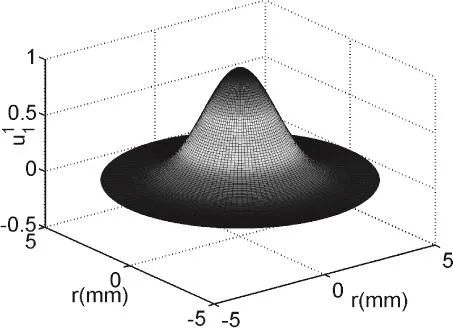
图2 覆盖阶梯电极的AT切石英晶体圆板厚度剪切振动的振动模态图。

这里阶梯电极的厚度分别为1/20h和1/15h。从图2可以发现，厚度剪切振动的能量大部分集中于圆板的中间，这样引起的能量耗散就比较合理[1]。进一步绘制出阶梯电极和均匀电极之间的模态振动比较如图3所示。

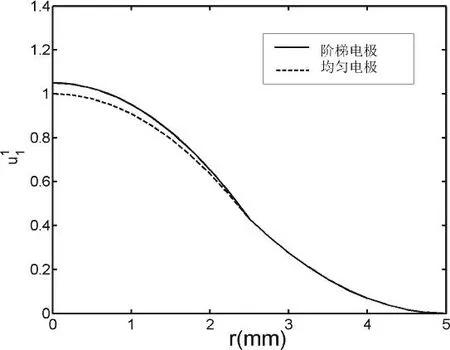
图3 不同电极形式下的厚度剪切振动模态图

从图3可以发现，无论是阶梯电极还是均匀电极，能陷效应都比较明显。当采用阶梯电极时，能陷效应更加明显，说明随着电极厚度的增加，振动能量更加集中于圆板中间。

3 结论

基于石英晶体圆板厚度剪切振动的位移假设和边界条件，建立了厚度剪切振动的频率方程。通过数值求解，获得覆盖阶梯电极的石英晶体圆板的厚度剪切振动的频率和振动模态。发现厚度剪切振动的振动能量主要集中于圆板的中间部位，这符合谐振器需要的能陷效应。相对于覆盖均匀电极，覆盖阶梯电极的能陷效应更加突出。本文的计算将为能量法计算能陷效应和预防能量衰减奠定了基础。

参考文献

[1]R.D. Mindlin, (J.S. Yang, Ed.). An introduction to the mathematical theory of vibrations of elastic plates[M].World Scientific, Hackensack, New Jersey, 2006.

[2]R.X. Wu, J. Wang, D.J. Huang, et al. The nonlinear thickness-shear vibrations of quartz crystal plates under an electric field[J]. International Journal of Nonlinear Mechanics, 61: 32-38, 2014.

[3]J.Wang,W.H.Zhao.The determination of the optimal length of crystal blanks in quartz crystal resonators[J]. IEEE Transactions on Ultrasonics Ferroelectrics & Frequency Control, 52(11): 2023-2030, 2005.

[4]吴荣兴,于兰珍,李继亮,等.石英晶体板高频振动的三维有限元分析[J].压电与声光, 36(5): 821-824, 2014.

[5]W.J. Wang, R.X. Wu, J. Wang, et al. Thickness-shear modes of an elliptical contoured AT-cut quartz Rresonator[J].IEEE Transactions on Ultrasonics, Ferroelectric, and Frequency Control, 60(6): 1192-1198, 2013.

[6]R. Bechmann. Elastic and piezoelectric constants of alphaquartz[J]. Physical Review, 110(5): 1060-1061, 1958.