基于Workbench的I-Lock螺旋升降柱静力分析
刘威,王杰,胡金龙,刘焕金
基于Workbench的I-Lock螺旋升降柱静力分析
刘威,王杰,胡金龙,刘焕金
(四川大学 制造科学与工程学院,四川 成都 610065)
螺旋升降柱及其构成的升降平台结构简单紧凑、易于控制,目前广泛用于舞台及各种工作平台的顶升。针对这种螺旋升降柱,介绍了其两种结构及工作原理。为进一步分析研究其静力特性,通过Solidworks对其“I-Lock”结构某型号建立模型,导入有限元分析软件ANSYS Workbench,建立了适当简化的两种高度的螺旋升降柱有限元模型并分别分析最大静载工况下的静力特性,研究了载荷对不同高度螺旋升降柱应力、位移大小与分布的影响。结果一方面证明了结构符合设计要求,另一方面也为结构的进一步设计优化提供了参考。
螺旋升降柱;静力分析;有限元模型;Workbench
螺旋升降柱作为一种独特的单作用直线运动机构,以其结构紧凑灵活、稳定性高、寿命较长和易于控制、同步等特点,在升降台上得到了广泛的应用。工业中大螺旋升降台主要用于物流、人员的升降运输以及零部件装配,如家居里的简易升降电梯、深度可调的活动底泳池以及大型剧院的舞台升降等。
从其运用场合可知,螺旋升降柱机构的可靠性与物资的安全、工程的安全乃至人的生命安全密切相关,但其结构较复杂,传统计算方法难以实现对结构的强度、刚度进行准确计算。利用有限元软件对结构进行模拟分析,能够定性乃至定量并直观地研究其在工作状态下的静力学特性,为机构的设计改进以及实际使用中出现的问题的解决提供思路和参考,最终提高机构的可靠性及安全性能。
1 螺旋升降柱简介
拥有加拿大技术专利的第一代螺旋升降柱于1988年在美国率先投入使用,第二年就成功取得了包括美国、中国在内的多国专利保护[1]。陈德生[2]等率先介绍了螺旋升降柱的工作原理并给出了主要参数;张颖等[1]和李伟[3]都对螺旋柱结构、工作原理、产品系列、布置方式以及使用注意事项进行了详细的阐述,后者还给出了设计选用方法。
所述结构如图1所示,其上半部分的螺旋柱状承载结构是由一条等厚度的竖直钢带B和一叠定截面的水平钢带A交替层叠构成。柱状结构的伸缩依靠的核心部件是同为螺旋布置的锥形辊子组D,通过外部传动机构带动螺旋辊子组绕螺旋线的中轴线顺、逆时针转动,可以实现螺旋升降柱的升、降。辊子组外侧的环形空间C用于存储剩余的竖直钢带,下部的柱状空间E用于存储剩余的水平钢带。
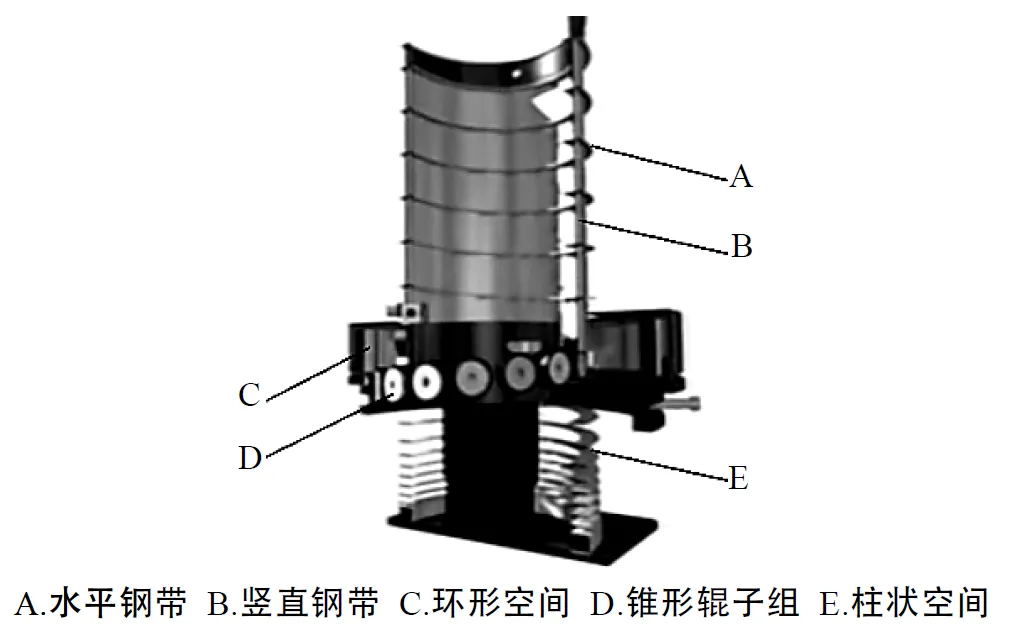
图1 传统大螺旋结构
整体结构之所以能够承载远高于钢带自重的外载荷,在于其堆叠构成的“工字”截面(如图2右侧),水平钢带中间的凹槽能够使竖直钢带嵌入其中,从而阻碍了钢带由堆叠到散开所存储的变形能的释放,即限制了钢带的弹性变形。第一代螺旋升降柱结构存在一定缺陷:结构对最低载荷有一定要求来保证螺旋柱的稳定性,整体柱状结构不能承受弯矩。

图2 传统大螺旋升降柱截面

图3 I-Lock结构大螺旋升降柱
第二代螺旋升降柱针对第一代传统螺旋升降柱结构的缺陷进行了改进,水平钢带的外边缘改为齿形,竖直钢带上下沿布置有孔,竖直钢带相邻两层有一定重叠,由水平钢带的齿插入孔中锁定。结构和螺旋柱截面如图3,被称为I-Lock结构。该结构不需要初始载荷,咬合的钢带能够有效承载更大的弯矩增加了整体结构刚度。
2 有限元模型的建立
2.1 三维模型建立及导入
分析针对PACO公司的I-Lock Spiralift(ILR250)型号(单节距型),由于整体模型结构复杂,接触部位多,考虑到划分网格后的计算效率,必须对结构做合理必要的简化,同时还可避免因模型的复杂而出现的影响计算效率与精度的畸形网格[4-6]。因此,参数化建模时只保留水平与竖直钢带的装配结构。仿真时将重点考察已经“自组装”好的螺旋柱工作状态下的应力、变形情况。
在Solidworks中建模可以实现与ANSYS Workbench(AWB)平台的三维几何模型无缝连接,几何相关参数以及其他参数如表1所示,螺旋拟定为9圈、5圈,建好的模型导入AWB-Transient Structure系统中的Geometry模块,并将水平钢带进行面分割操作以供后续约束施加。

表1 ILR250型号参数
2.2 材料定义及网格划分
材料AISI301,弹性模量为200 GPa,泊松比为0.28,密度为7800 kg/m3,屈服极限965 MPa。该材料对应国标为1Cr17Ni7,钢带型材经冷作硬化后室温下屈服强度不低于960 MPa,抗拉强度不低于1275 MPa[7]。
良好的网格布置是应用有限元法进行结构仿真时提高仿真可信度的关键要素之一[8],网格形状、疏密程度与被分析结构相适宜的网格划分能够在节省计算成本的同时得到足够精度的仿真结果。由于分析对象水平、竖直钢带均为等壁厚薄壁特征,因此模型建立时只建立面体,在AWB中将用壳单元划分,与实体单元划分相比能够得到数量少、质量高且疏密适宜的网格。通过总体和局部网格控制,两种高度的升降柱得到的网格平均质量分别为0.86362、0.94078,共105362、91829个节点、133476、118977个单元。总体有限元模型以及局部网格特征分别见图4和图5。

图4 I-Lock大螺旋升降柱有限元模型
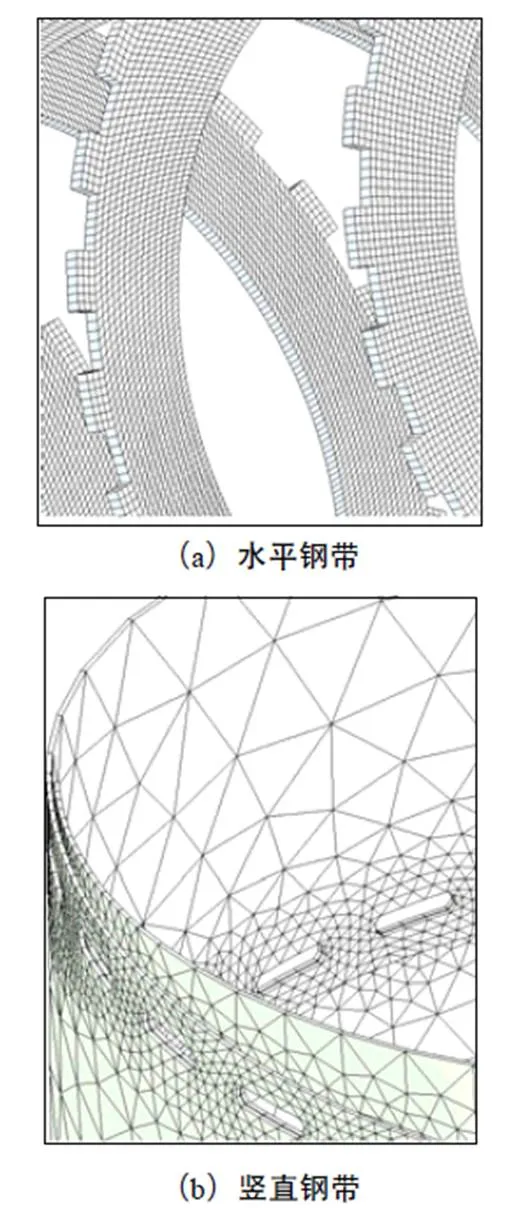
图5 局部网格
2.3 接触分析及设定
I-Lock螺旋结构中接触繁多,需要根据实际情况进行取舍和简化以节约计算成本和减少非线性程度并同时得到不错的收敛特性和求解精度[9]。水平钢带与竖直钢带之间的接触主要涉及的接触见表2。由于不锈钢之间无润滑干摩擦下的摩擦系数取=0.15,摩擦角=arctan约为8.53°,而螺旋结构螺旋升角1=arctan(/π)约为7.83°小于摩擦角,所以主要考虑接触1为主的承载接触,忽略接触2。考虑到接触3、4理想状态下对结构影响小,且为实现保留价值只能设置为有摩擦接触增加非线性因素使得求解困难,优先考虑忽略,若在理想状态下变形显示该区域几何重叠则应重新考虑。

表2 水平、竖直钢带主要接触分析
2.4 约束与载荷
考虑上端加载平台对螺旋上部的固定作用,对上部水平、竖直钢带末端边缘添加运动副Joint并限制为只能竖直平移;对水平钢带下部三圈的表面施加Frictionless Support模拟辊子组对水平钢带提供的竖直支撑力;对水平、竖直钢带下部末端施加Simply Support模拟停机时储存的剩余钢带对整体结构的约束作用。
对竖直钢带顶部施加竖直向下的最大静载力75000 N;施加标准重力加速度9806.6 mm/s2。约束与载荷示意图见图6。
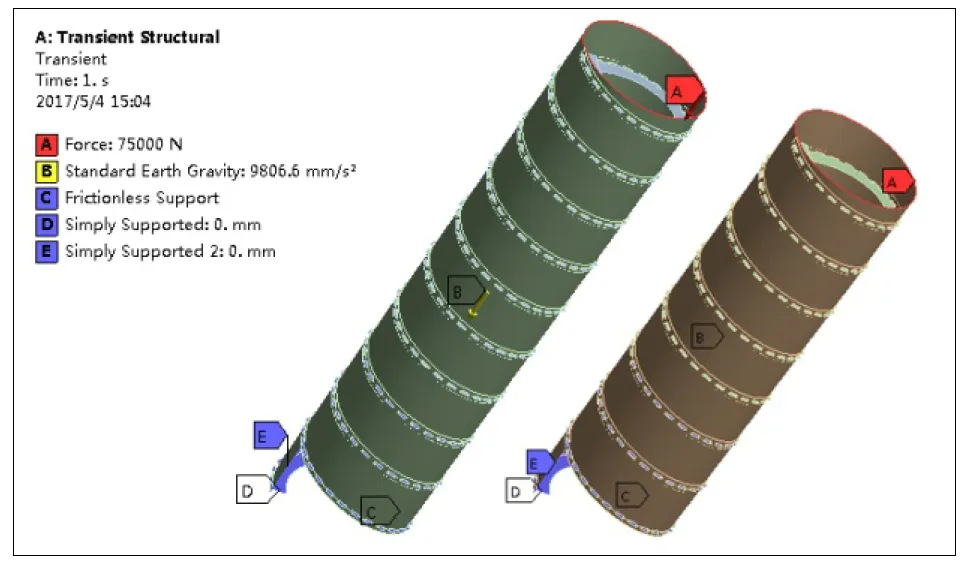
图6 约束与载荷示意图
3 静力分析结果与评估
3.1 等效应力
两种高度结构等效应力云图如图7,可看出相同载荷与约束下,两种高度螺旋结构总体应力分布相似,数值相近,但个别部位存在较严重的应力集中现象。一方面由于竖直钢带孔的接触面小且为壳单元的厚度面,容易产生接触应力集中。另一方面由于简化产生了a、b、c三个超过材料屈服极限的大应力区域以9圈螺旋结构为例见图8。
图7 等效应力云图
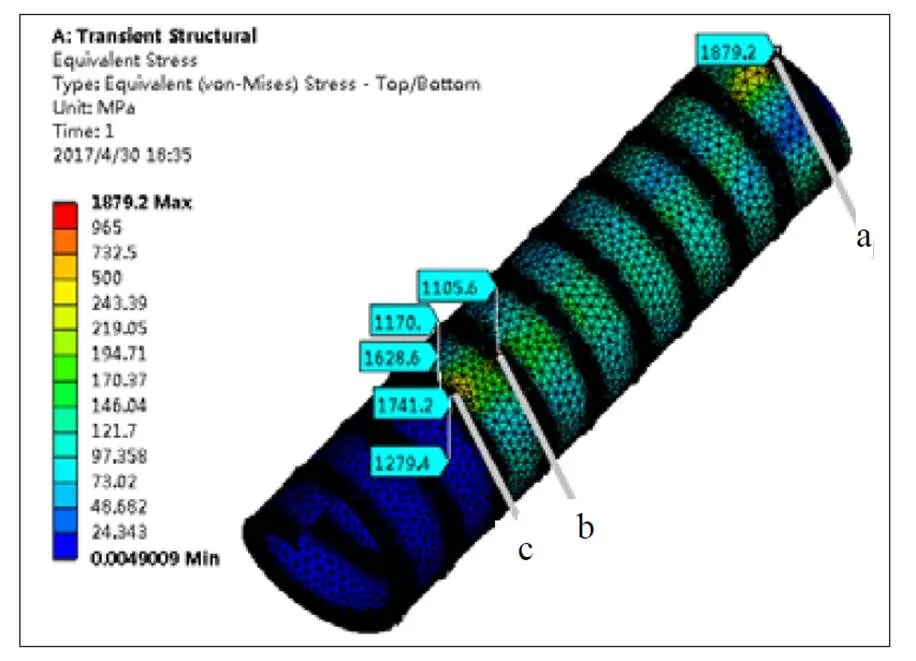
图8 9圈螺旋结构等效应力云图及大应力区域
a区域由于简化了加载结构造成了局部应力集中,细节上不再具备参考价值。b、c区域由于水平钢带支承边界(c区域)的存在使得结构的变形突然受限,类似一端固支的悬臂梁根部情况,导致应力的急剧变化如图9所示。
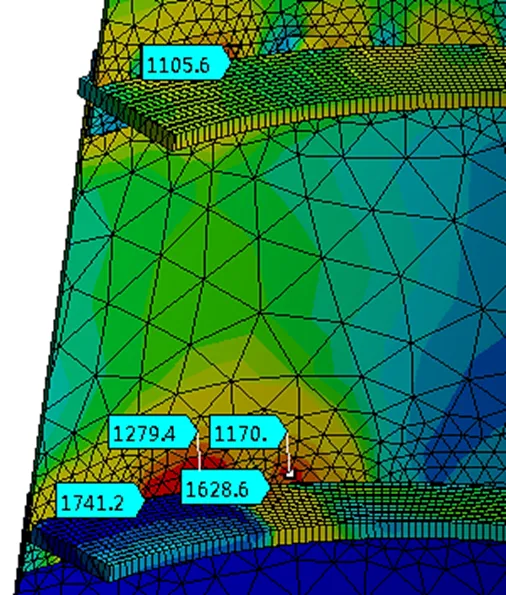
图9 大应力区域b、c应力详图
c区域上方竖直钢带类似悬臂梁,使得b区域成为因此受影响最大的另一区域。辊子组实际支承刚度小于Frictionless Support模拟的支承刚度,且实际应用中不存在屈服变形,因此适当降低支承刚度能够避免该情况。
两种高度结构的竖直钢带外壁等效应力总体上在50~170 MPa范围波动;啮合区域应力在周向呈规律变化(以9圈螺旋结构为例,如图10),竖直钢带孔周等效应力普遍从550±100 MPa左右向周边递减,水平钢带等效应力从外侧齿间区域普遍从300±50 MPa左右向周边递减。
3.2 位移
位移关注点为平台最高点,由于初始状态水平钢带的齿位于竖直钢带的孔中心,齿上下面均有约为0.5 mm的初始间隙,所以加载过程中最大位移分为两个阶段:开始为消除啮合间隙阶段,之后为无间隙正常承载阶段如图11。
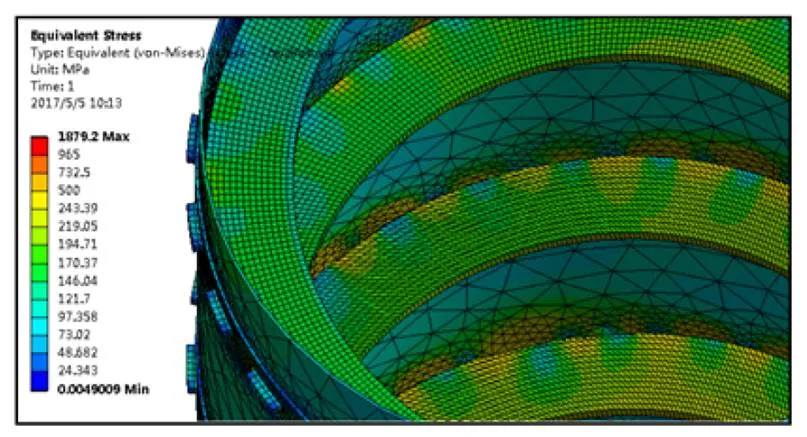
图10 整体结构等效应力周向分布图

图11 加载前后结构间隙对比图
最大位移与时间的变化关系如图12。可以看出螺旋圈数分别为7圈、9圈(支承外承载圈数分别为5圈、7圈)的I-Lock螺旋结构经过加载消除了间隙后,竖直方向最大位移量与载荷的变化关系可近似为线性。将数据读入MATLAB并将时间步换算为对应载荷步并对载荷-竖直方向位移用一阶方程做拟合,结果见图13、图14。由两拟合直线方程的比例系数可知5圈与7圈螺旋结构的静刚度分别为7.13×107N/m与5.75×107N/m,高度高的螺旋结构结构静刚度低。最大接触滑动距离5圈与7圈螺旋结构的分别为1.0536、1.4135说明刚度的降低受接触区域滑动影响。
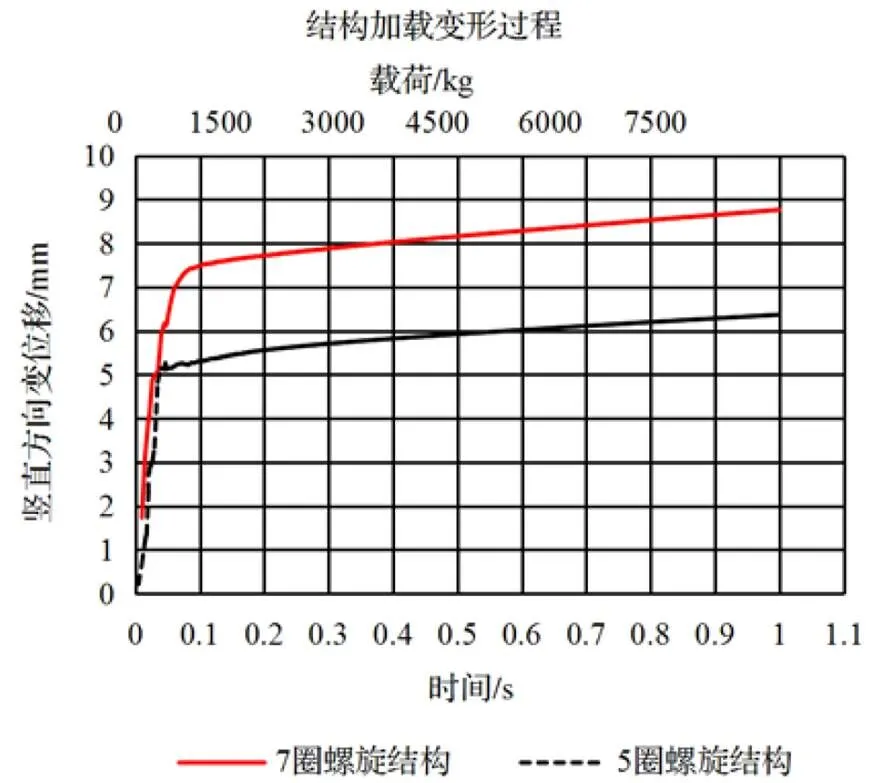
图12 不同高度螺旋升降柱加载变形图

图13 5圈螺旋结构力-位移拟合结果

图14 7圈螺旋结构力-位移拟合结果
4 结论
对I-Lock螺旋升降柱结构以及工作状况简化并建立有限元模型分析其静力特性得出以下结论:
(1)I-Lock螺旋升降柱的顶端加载平台与下端支承影响整体结构的最大应力。结构上采取措施适当降低支承刚度能够使得支承区域避免过大的应力。
(2)在最大静载下结构的等效应力除应力集中区域外均小于材料屈服极限965 MPa,满足设计要求。
(3)竖直钢带孔边缘强化后能够提升整体结构静载安全系数。水平钢带可根据竖直钢带结构安全系数进行适当精简。
(4)I-Lock螺旋升降柱承载时具有稳定的静刚度,高度越高的螺旋结构静刚度越低,研究螺旋柱高度-载荷-刚度之间的对应关系能够在控制定位时进行补偿。
(5)非线性求解力收敛残差最终分别稳定在300~500 N、70~300 N范围,表明求解精度仍有待提高以更加准确地对结构做定量分析。
[1]张颖,段慧文. “大螺旋”在剧院领域的应用[J]. 演艺科技,2005(5):30-34.
[2]陈德生,曹志锡. 螺旋升降柱[J]. 起重运输机械,2004(1):39-40.
[3]李伟. 自组式螺旋升降机[J]. 有色设备,2005(4):10-12.
[4]Champion. E. R. Finite element analysis in manufacturing engineering[J]. New York:Mcgraw-Hill, inc,1992:1-18.
[5]马青. 履带起重机臂架有限元简化模型稳定性分析[D]. 大连理工大学,2009:18.
[6] 张梦超,王杰,李祥,等. 基于Workbench的组装式液压门式起重机结构模态分析[J]. 机械,2017,44(2):17-20.
[7]成大先. 《机械设计手册》第六版(第1卷)[M]. 北京:化学工业出版社,2016.
[8]李涛,左正兴,廖日东. 结构仿真高精度有限元网格划分方法[J]. 机械工程学报,2009,45(6):304-308.
[9]夏卫明,骆桂林,嵇宽斌. 橡胶结构有限元分析收敛问题的对策[J]. 机械设计与制造,2013(7):265-268.
Static Analysis of the I-Lock Spiralift Based on Workbench
LIU Wei,WANG Jie,HU Jinlong,LIU Huanjin
( College of Manufacturing Science and Engineering,Sichuan University,Chengdu 610065,China)
Spiralift and the lifting platform are simple in structure and easy to control. They are widely used on the lifting of the stage and working platforms at present. This paper introduces the structures and the working principle of the spiralift. A specific model of its I-Lock structure is built in SolidWorks, and two simplified finite element models of different height are built in ANSYS Workbench then for further study on its static characteristics. The paper studies the effect of load on the value and distribution of stress and deformation of the two different height structures under the maximum static load condition. The result testifies that the structure satisfies the design requirements and provides a reference for the further optimization design on the structure.
spiralift;static analysis;finite element model;Workbench
TU311.1
A
1006-0316 (2018) 04-0018-06
2017-08-23
刘威(1992-),男,宁夏银川人,硕士研究生,主要研究方向为计算机辅助设计与制造;王杰(1964-),男,四川成都人,博士,教授、博士生导师,主要研究方向为计算机辅助设计与制造、企业信息化与系统集成。
10.3969/j.issn.1006-0316.2018.04.005

