不同载荷下灭弧室瓷套应力分析及临界裂纹研究

李旭

（三峡大学电气与新能源学院新能源微电网湖北省协同创新中心，湖北宜昌 443002）

0 引言

高压断路器灭弧室瓷套属于电瓷类产品，具有优良的机械强度和电气绝缘性能，但在拉应力作用下容易发生脆断现象，严重影响电力设备及系统的安全稳定运行。为正确检测评估瓷套的健康状况，需选择合适灵敏度的检测仪器，并给出评价瓷套的参考裂纹尺寸，因此，研究灭弧室瓷套在运行过程中受到不同载荷作用下的应力分布特征及相应的最小临界裂纹尺寸，为瓷套运行状况的评估检测提供可靠的参考和理论指导，对电力系统的安全稳定运行具有重要的意义。

文献[1]根据建立的有限元仿真模型计算分析了支柱瓷绝缘子在静态载荷下的应力分布及表面裂纹的应力场强度因子。文献[2]建立了瓷绝缘子的有限元模型，计算了其应力分布情况及临界裂纹尺寸的大小。文献[3]对不同热载荷条件下的瓷套应力分布进行了分析，并研究了热应力对其结构强度的影响。文献[4]通过简化的支柱瓷绝缘子力学模型分析了静态载荷下的最大拉应力值及断裂的临界裂纹尺寸。文献[5]通过建立的瓷套力学分析模型，分析了金属法兰在多种安装方式下的瓷套受力大小及分布。以上文献只对静态载荷下瓷套和瓷绝缘子等电瓷类产品的应力分布进行了计算分析，并未研究动态载荷下的应力分布特征及相应的断裂临界裂纹尺寸。

笔者建立了高压断路器灭弧室瓷套有限元仿真模型和短路电动力作用模型、动态风力作用模型，计算分析了瓷套在静态载荷及短路电动力、动态风力载荷作用下的应力分布情况及相应的临界裂纹尺寸大小，为瓷套的运行维护提供参考和借鉴[6]。

1 断路器灭弧室瓷套有限元仿真模型

1.1 灭弧室瓷套的基本结构

笔者以500 kV某高压SF6断路器为例，其灭弧室瓷套主要由法兰、胶装水泥、瓷件本体、高压接线板和外接导线等部分组成，见图1。灭弧室瓷套的瓷件本体采用的是高强度氧化铝陶瓷材料，起承载和绝缘作用；法兰采用的是铸铜材料，起固定连接作用；胶装水泥为填充于法兰和瓷件本体之间空隙处的填充剂，瓷套通过自由侧的高压接线板与外接导线相连，形成电流通道。断路器灭弧室瓷套在其运行过程中的受力主要包括自身及高压接线板等附件的重力、瓷件本体内SF6气体的压力、热应力、外接导线拉力等静态载荷力和短路电动力、动态风力等动态载荷力[7]，该灭弧室瓷套的主要尺寸参数和组成部分材料性能参数分别见表1和表2。

图1 高压断路器灭弧室瓷套基本结构Fig.1 Basic structure of high voltage circuit breaker arcing chamberporcelain bushing

表1 瓷套主要尺寸参数Table 1 The main size parameters of porcelain bushing

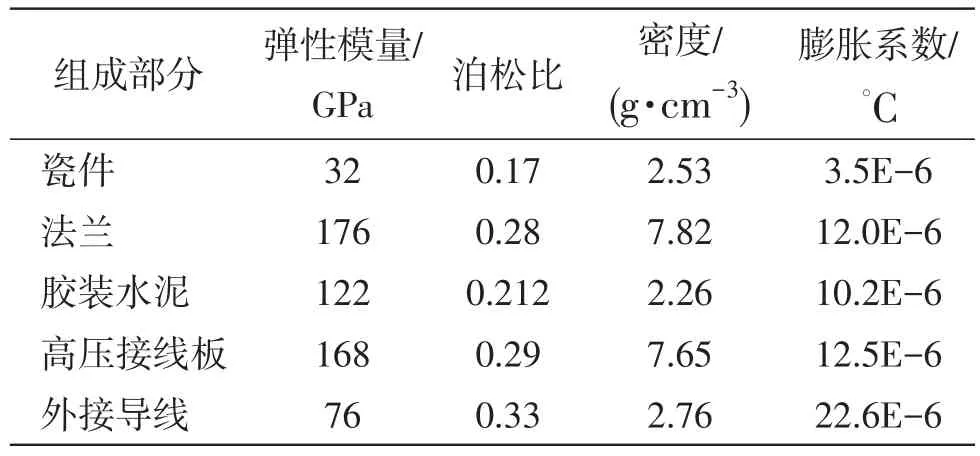
表2 瓷套组成部分主要材料性能参数Table 2 The main material performance parameters of porcelain bushing component

1.2 灭弧室瓷套有限元仿真模型

有限元法是一种求解偏微分方程的数值方法，它以变分原理和加权余量法为基础[8]，最早应用于结构力学领域，后来随着计算机技术的发展，有限元法在流体力学、电磁场等各工程领域的建模仿真分析中获得了广泛的应用，并在实践过程中被证明是一种可靠实用的仿真分析方法，有限元法为工程人员带来了很大的方便和效益，有限元分析的基本流程见图2。

图2 有限元分析的基本过程Fig.2 Basic process of finite element analysis

高压断路器灭弧室瓷套多运行于复杂的户外环境中，根据相关文献[9-10]的研究显示，灭弧室瓷套在冬季低温条件下的运行环境最为恶劣，瓷套要承受一个因组成部分材料线膨胀系数不一致而产生的温度热应力作用，而因电流作用产生的电动力及导线的重力则通过瓷套自由侧的高压接线板作用于瓷套上，对瓷套产生一个力矩作用。本文基于瓷套的结构及运行状况，采用有限元法建立的灭弧室瓷套有限元仿真模型见图3。为便于有限元的计算分析，认为瓷套组成部分材料的各向性质相同，不考虑材料热电效应的影响。设置的主要边界条件有：重力加速度为9.8 m/s2，内置SF6气体的压力为0.69 MPa，热应力参考温度取热膨胀计算中的标准参考温度18℃，为获得本文研究所要计算的最小临界裂纹尺寸，瓷套运行环境温度设置为冬季最低温-6℃。

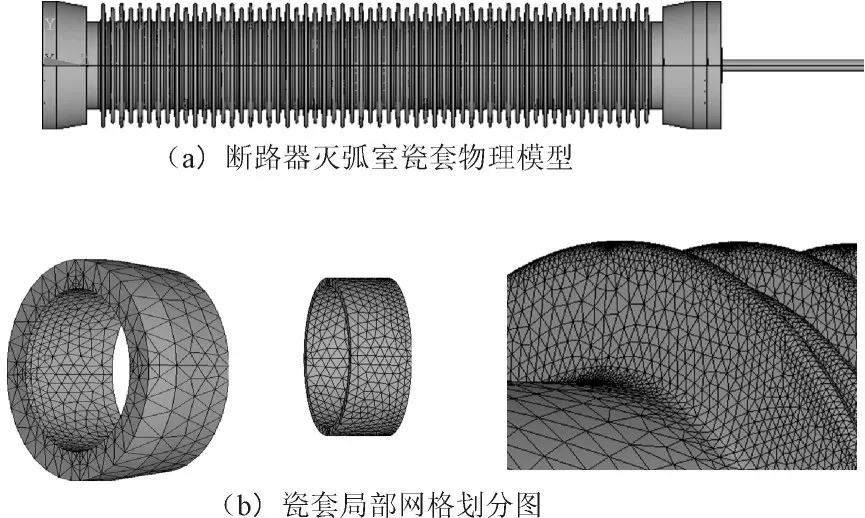
图3 断路器灭弧室瓷套有限元仿真模型Fig.3 Finite element simulation model of circuit breaker arcing chamberporcelain bushing

2 瓷套应力分布计算与分析

笔者研究的高压断路器灭弧室瓷套的瓷件本体采用的是陶瓷脆性材料，在拉应力的作用下，易产生裂纹而发生断裂事故，经研究发现：瓷套的断裂一般均由瓷件本体的裂纹扩展产生[11]，其断裂存在一个相应的临界裂纹尺寸。笔者采用有限元法对瓷套进行应力分析，分析瓷件本体的应力分布情况及最大拉应力所在的位置，并确定瓷套断裂所对应的临界裂纹尺寸大小，分析时以瓷套的瓷件本体拉应力为主，在应力分布云图中为拉应力。

2.1 静态载荷作用下的瓷套应力分析

瓷套运行时所受的静态载荷主要有自身及附件的重力、内置SF6气体的压力、热应力、外接导线拉力等，瓷套在静态载荷作用下的有限元应力仿真计算结果见图4和图5。

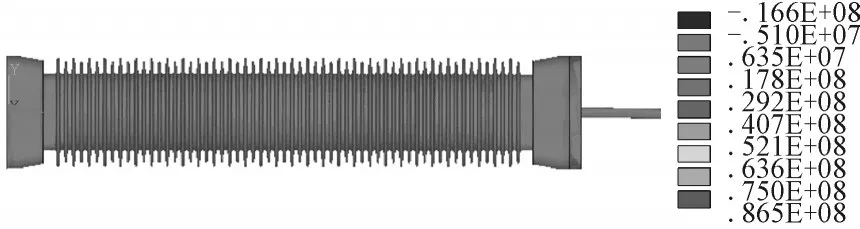
图4 灭弧室瓷套整体应力分布图Fig.4 The overall stress distribution of arcing chamber porcelain bushing

图5 瓷件本体应力分布Fig.5 The stress distribution of bulk porcelain bushing

图4为灭弧室瓷套整体的应力分布云图，由于瓷套的断裂一般均发生在瓷套瓷件本体，本文主要研究的是瓷件本体的应力分布情况及临界裂纹尺寸大小，因此本文单独取瓷件本体的应力分布云图进行显示，以便于观察。由灭弧室瓷套应力的有限元仿真计算结果可知，该灭弧室瓷套瓷件本体在静态载荷下的最大拉应力为27.2 MPa，位置为法兰口外瓷件本体上端部约0.6 mm处。

2.2 短路电动力载荷作用下的瓷套应力分析

2.2.1 短路电动力载荷作用模型

高压断路器所在的线路发生短路故障时，其外接导线流过的电流值将急剧增加，导线将受到很大的电动力作用，使瓷套承受一个随着短路电流而动态变化的载荷力，计算电动力的方法主要有毕奥-萨伐尔定律法和能量平衡法，毕奥-萨伐尔定律法不需要知道自感、互感等参数，更加方便实用[12]，因此本文采用毕奥-萨伐尔定律法来计算电动力。笔者以系统中发生概率最高的单相接地短路为例，根据毕奥-萨伐尔定律法，单相接地短路时，故障相导线所在的磁场由两非故障相电流和地电流共同产生，导线在两非故障相电流磁场中的受力为水平方向；故障相电流与地电流方向相反，相关研究表明:当单相接地短路引起的地电流全部从故障相导线正下方的“等效地导线”流过时，导线所受的电动力最大，方向为竖直向上[13]。本文计算的是最小临界裂纹尺寸，非故障相电流要比短路电流小得多，其对故障相导线的电动力作用相比“等效地导线”电流要小得多，因此可忽略其影响，则单相接地短路电流及最大电动力可表示为

式中：Is为短路电流周期分量的有效值；α为电流非周期分量的衰减系数，一般取为22.31 s-1。

本文所分析的断路器的高度h为=8 000 mm，外接导线长度l=4 600 mm，短路电流周期分量有效值取该断路器额定开断电流Is=42 500 A，则根据式（1）和式（2）可得到单相接地短路时的电动力波形图，见图6。由图6可知，电动力是周期性衰减的，在t=0.009 8 s时电动力取得最大值，为1 348.5 N。

2.2.2 短路电动力作用下瓷套应力分析

瓷套外接导线所受的短路电动力通过高压接线板作用在灭弧室瓷套上，利用本文建立的灭弧室瓷套有限元仿真模型，将所计算得到的单相短路电动力施加到该仿真模型上，则仿真得到的瓷套瓷件本体在自身及附件的重力、内置SF6气体的压力、热应力、外接导线拉力等静态载荷和短路电动力动态载荷共同作用下的最大拉应力变化情况见图7。由图7可知，瓷套的瓷件本体的最大拉应力值在t=0.010 2 s时达到最大，此时的瓷件本体的应力分布见图8。

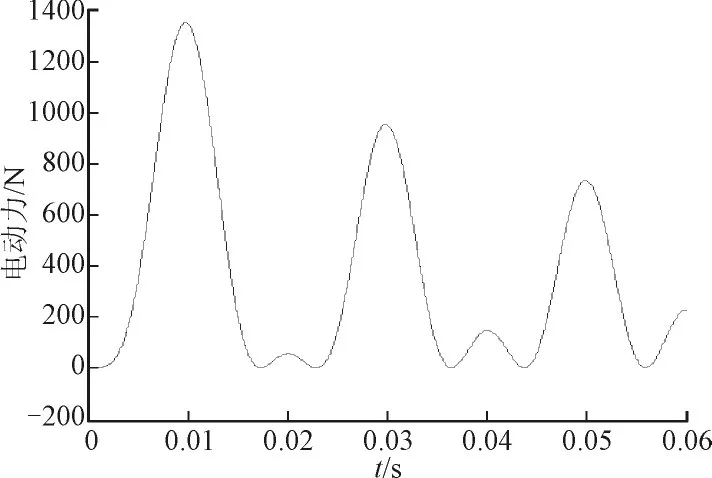
图6 单相短路时的电动力波形图Fig.6 The wave of single phase short circuit electrodynamic force

图7 单相短路故障时瓷件本体最大拉应力时程图Fig.7 The time-history diagram of porcelain body maximum tensile stress under single phase short circuit fault

图8 t=0.010 2 s时瓷件本体应力分布Fig.8 The stress distribution of porcelain body when t=0.010 2 s

2.3 动态风载荷作用下的瓷套应力分析

2.3.1 动态风载荷作用模型

实测资料研究发现，风可近似表示成一个较长周期的平均风和一个较短周期的脉动风。平均风速随高度不同而变化，其规律可用指数律来表示，脉动风则多采用风速功率谱来进行模拟，Davenport脉动风速谱[14]是有效实用的功率谱理论，在世界各国中得到了广泛的应用。作用在结构上任一点处的风速可表示成：

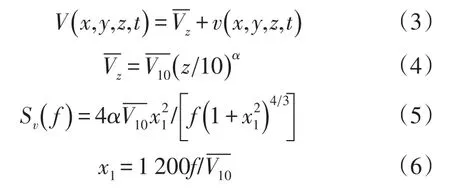
式中：Vˉ、v分别表示风的平均风和脉动风两个组成部分；Sv（f）表示功率谱密度；f表示脉动风频率；x、y、z表示空间坐标向量；表示z=10 m标准高度处的平均风速；ɑ表示地表的粗糙度系数。

对于脉动风速谱的模拟方法主要包括线性滤波法和谐波叠加合成法[15]。AR自回归法因具有更高的计算效率，且将风速的时间相关性考虑在内，在工程领域中对模拟风速方面得到了有效的认证和广泛的应用。根据AR自回归法得到空间相关脉动风速为

式中：N（t）为独立随机过程向量；ψk为自回归系数矩阵；p表示该模型的阶数大小；∆t表示所模拟的风速的时间步长；X、Y、Z为空间坐标向量。

基于相关函数理论和随机振动理论，对式（7）进行相应的求解，将其时间步长离散化，并设初始时刻之前的风速为0，则得到的递推矩阵可表示为

本文近似认为灭弧室瓷套的各受风面所在高度相同，标准高度10 m处的平均风速按电力行业相关抗风标准取为25 m/s，地面粗糙度系数K=0.16，动态风的时间段长度取160 s，时间步长∆t=0.2 s，则利用MATLAB软件，基于Davenport脉动谱和AR自回归法仿真模拟得到的风速时程曲线见图9。

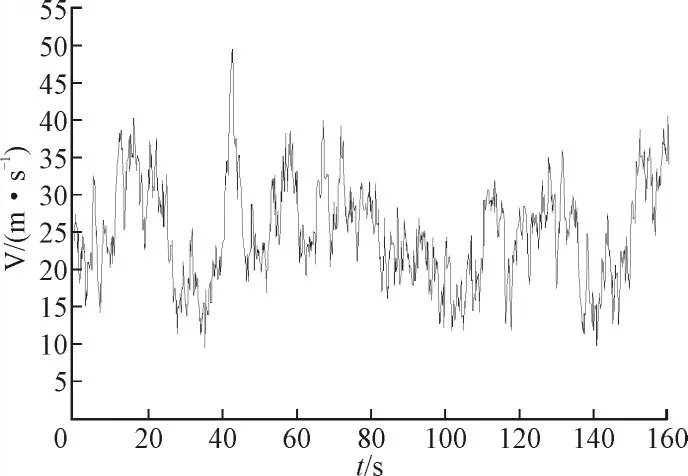
图9 风速时程曲线Fig.9 The time-history curve of wind speed

根据国家相关标准和规范，将风速转化为相应的风压[16]，则断路器灭弧室瓷套所受的风载荷可按下式进行计算：

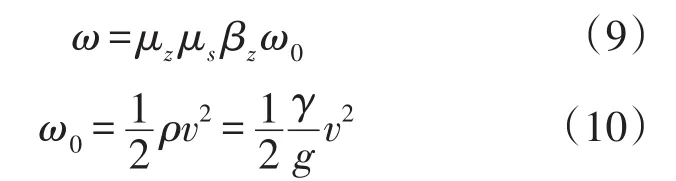
式中：ω0=v2/1600表示基本风压的标准值；μz、βz分别表示高度为Z处的风压高度变化系数和风振系数；μs则为体型系数。

2.3.2 动态风载荷作用下的瓷套应力分析

利用图9模拟得到的风速时程曲线，根据式（9）和式（10）将其转化为相应的风压，并施加到本文所建立的灭弧室瓷套有限元仿真模型的受风面上，则仿真得到的瓷套在自身及附件的重力、内置SF6气体的压力、热应力、外接导线拉力等静态载荷和动态风载荷载荷共同作用下的最大拉应力变化情况见图10。由图可知，当t=42.6 s时，灭弧室瓷套瓷件本体的最大拉应力达到最大值，此时的瓷件本体应力分布云图见图11。由图11可知，该高压断路器灭弧室瓷套本体在静态载荷和风力动态载荷共同作用下的最大拉应力所在位置在瓷件本体中间部分，其值为30.8 MPa。

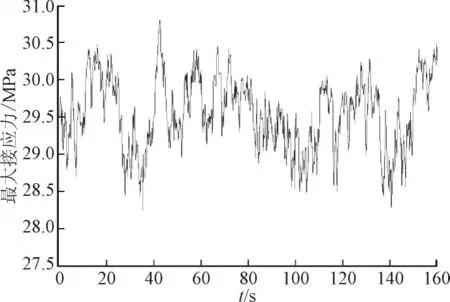
图10 风载荷下瓷件本体最大拉应力时程曲线Fig.10 The time-history curve of maximum tensile stress of the porcelain body loaded by wind

图11 t=42.6 s时瓷件本体应力分布Fig.11 The stress distribution of porcelain body when t=42.6 s

3 瓷套临界裂纹尺寸计算与分析

根据断裂力学的理论[17-18]：位于瓷质材料表面的裂纹缺陷要比其内部裂纹缺陷严重的多。瓷套的断裂一般均发生在瓷件本体，因此本文主要对灭弧室瓷套瓷件本体表面的裂纹缺陷进行研究，则由断裂力学的理论可以得到：

式中，

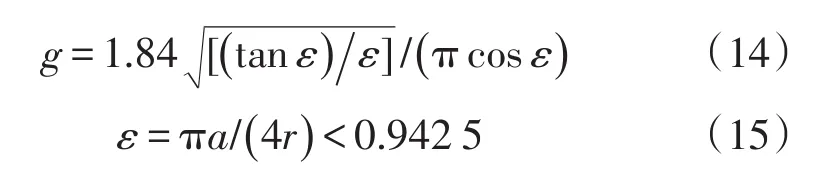
式中：Yσ为I型裂纹应力强度因子的函数，fw为修正系数，其值为1，σmax为瓷套表面所受的最大拉应力值，Mm为放大因子，其值也为1，M为膨胀系数，a为瓷件本体表面的轴类半椭圆裂纹尺寸，r=140 mm，为瓷件本体轴半径。

将式（11）—式（15）进行整理，可得到临界应力强度因子KIC与临界裂纹尺寸acr之间的关系

式中，

本文研究的瓷套瓷件本体所采用的氧化铝陶瓷的临界应力强度因子KIC=3.92 MPa·m1/2，根据前面计算得到的不同载荷下的最大拉应力值，由式（16）和（17）计算得到对应的临界裂纹尺寸及相应的验证值见表3。

表3 不同载荷下的瓷套临界裂纹尺寸Table 3 The critical crack size of porcelain bushing under different load

由表3可知，计算得到的εcr均小于0.942 5，满足式（15）的要求，所求得不同载荷下的临界裂纹尺寸是有效的，当瓷套在静态载荷作用时，再受到一个短路电动力或动态风力载荷的作用，瓷件本体的临界裂纹尺寸均有不同程度的减小，当对现场运行的瓷套健康状况进行检测评估时，需根据其临界裂纹尺寸大小选择合适的裂纹检测仪器，并考虑短路电动力和动态风力的影响。

4 结论

研究了不同载荷作用下高压断路器灭弧室瓷套的应力分布情况及断裂所对应的临界裂纹尺寸大小，根据有限元理论，建立了灭弧室瓷套的有限元仿真计算模型，并基于毕奥-萨伐尔定律建立了短路电动力作用模型，由Davenport谱理论和AR法建立了动态风载荷作用模型，分析了瓷套在自身及附件的重力、内置气体的压力、热应力、外接导线拉力等静态载荷作用下的应力分布情况，以及静态载荷与短路电动力或动态风力载荷联合作用下的应力分布情况。结合不同载荷下瓷套应力分布情况和断裂力学的相关理论，计算出了瓷套在静态载荷作用下的临界裂纹尺寸为2.93 mm，静态载荷与短路电动力、动态风力载荷联合作用下的临界裂纹尺寸分别为2.69 mm、2.76 mm，本文研究成果可为瓷套运行状况的检测评估提供理论参考和借鉴。

参考文献：

[1]肖汉宁，彭苏华，高朋召.支柱瓷绝缘子表面裂纹应力强度因子的有限元分析[J].湖南大学学报:自然科学版，2014，41（12）：53-58.XIAO Hanning，PENG Suhua，GAO Pengzhao.Stress in⁃tensity factor analysis of surface crack on rod porcelain in⁃sulator through finite element method[J].Journal of Hunan University Natural Sciences，2014，41（12）:53-58.

[2]徐连勇，荆洪阳，霍立兴，等.在役含缺陷棒形悬式瓷绝缘子的非破坏性可靠性评定[J].天津大学学报，2006，39（10）：1258-1263.XU Lianyong，JING Hongyang，HUO Lixing，et al.Nonde⁃structive evaluation of reliability with creeping wave for porcelain rod suspension insulator served[J].Journal of Tianjin University，2006，39（10）:1258-1263.

[3]YAO X，GENG Y，LIU Z，et al.Mechanical reliability of a 126 kV single-breakvacuum circuit breaker[C]//Reliabili⁃ty and Maintainability Symposium（RAMS），2015 Annu⁃al.IEEE，2015.

[4]李晓红，刘叙笔，张杰，等.支柱瓷绝缘子断裂临纹尺寸的分析与计算[J].高电压技术，2004，30（z1）：102-103.LI Xiaohong，LIU Xubi，ZHANG Jie，et al.Analysis and calculation of critical crack dimension of fracture in the struct porcelain insulator[J].High Voltage Engineering,2004，30（136）:102-103.

[5]SETHI B K.Ways and means to increase the mechanical strength of cylindrical porcelain insulator and bushing[J].Transactions-Indian Ceramic Society，2014，24（1）:243-246.

[6]肖鱼.高压断路器灭弧室瓷套应力分析与临界裂纹研究[J].电瓷避雷器，2017（3）：193-198.XIAO Yu.Stress analysis and critical crack research of high voltage circuit breaker arcing chamber porcelain bushing 2017（3）：193-198.

[7]魏光大，徐如恬.SF6瓷套破坏原因的试验分析[J].中国电瓷，1984（5）：10-17.WEI Guangda，XU Rutian.Experimental ansys for destruc⁃tion causes of SF6 porcelain bushing[J].Insulators and Surge Arresters，1984（5）:10-17.

[8]OSTRENKO M V，ANDRIIENKO B Y，RYZHYI V N.Fi⁃nite element method application for HVDC electrical insu⁃lation strength problems solution[C]//IEEE Region 8 Inter⁃national Conference on Computational Technologies in Electrical and Electronics Engineering.IEEE，2010:714-716.

[9]HAN S W，CHO H G，CHOI I H，et al.Failure character⁃istics of suspension-type porcelain insulators on a 154 kV transmission line[C]//Electrical Insulation,2006.Confer⁃ence Record of the 2006 IEEE International Symposium on.IEEE,2006:118-121.

[10]高千秋.电器瓷套的低温特性探讨[J].电瓷避雷器，2002（1）：13-16.GAO Qianqiu.Behaviour of apparatus insulators at low temperature[J].Insulators and Surge Arresters，2002（1）:13-16.

[11]龚江宏.陶瓷材料断裂力学[M].北京：清华大学出版社，2001.

[12]杨武，荣命哲，王小华，等.考虑电动力效应的高压断路器动力学特性仿真分析[J].中国电机工程学报，2003，23（5）：103-107.YANG Wu，RONG Mingzhe，WANG Xiaohua，et al.Dy⁃namic simulation of high-voltage circuit breaker consider⁃ing electro dynamic force[J].Proceedings of the CSEE，2003，23（5）:103-107.

[13]霍宏艳，肖石，闻映红.地电流的建模仿真分析[J].铁路计算机应用，2011，20（3）：5-8.HUO Hongyan，XIAO Dan，WEN Yinghong.Simulation analysis on ground current[J].Railway Computer Applica⁃tion，2011，20（3）:5-8.

[14]WANG Y D，LI C X.Simulation of fluctuating wind speeds based on data-driven approaches[J].Applied Mechanics&Materials，2014，635-637.

[15]孙芳锦，顾明.基于小波方法的空间风速场模拟[J].同济大学学报:自然科学版，2011，39（11）：1581-1585，1651.SUN Fangjin，GU Ming.Spatial wind field simulation based on wavelet method[J].Journal of Tongji University（Natural Science），2011，39（11）:1581-1585，1651.

[16]张东，董新胜，陶凤源，等.减少季风对输电线路绕击影响的研究[J].电瓷避雷器，2014（3）：57-61.ZHANG Dong，DONG Xinsheng，TAO Fengyuan，et al.Re⁃search on reduction of the monsoon influence on the trans⁃mission line shielding failure[J].Insulators and Surge Ar⁃resters，2014（3）:57-61.

[17]KRUZIC J J，CANNON R M，RITCHIE R O.Crack-Size effects on cyclic and monotonic crack growth in polycrys⁃talline alumina:quantification of the role of grain bridging[J].Journal of the American Ceramic Society，2004，87（1）:93-103.

[18]SUO Z，KUO C，BARNETT D，et al.Fracture mechanics for piezoelectric ceramics[J].Journal of the Mechanics&Physics of Solids，1992，40（4）:739-765.