BCH-代数的路径∗

李金龙

(陕西理工大学数学与计算机科学学院，陕西汉中723000)

文[1]中作者在BCH-代数中引入了质子的概念，证明了有限偏序BCH-代数一定存在质子，说明了一般的BCH-代数可能存在质子也可能不存在质子，并借助于质子对BCH-代数的子代数进行了一些研究.在本文中，作者将利用质子这一概念在BCH-代数中引入路径的定义，并对BCH-代数的路径进行一些研究，特别是要对有限偏序BCH-代数的路径进行研究.同时在BCHK-代数中引入不变质子的概念，并对BCHK-代数中的不变质子进行研究.

1 预备知识

定义1[2]一个(2，0)型代数〈X﹔∗，0〉叫做BCH-代数，如果∀x,y,z∈X，它满足下列公理：

H-1x∗x=0;H-2x∗y=y∗x=0⇒x=y;H-3(x∗y)∗z=(x∗z)∗y.

定义2[1]设〈X﹔∗，0〉是一个BCH-代数，b∈X，若x∈X，b∗x=0，即b≤x，则x=b(即b∈X，∀x∈X，若x6=b，则b∗x6=0)，称b是X的一个质子.

定义3[3]设〈X﹔∗，0〉是一个BCH-代数，若∀x∈X，有0∗x=0成立，则称〈X﹔∗，0〉是一个BCHK-代数.

定义4[4]设〈X﹔∗，0〉是一个BCH-代数，元素a∈X，若x∈X，x∗a=0，即x≤a，则x=a，就称元素a为X的一个原子.

文[4]指出，元素0是BCH-代数〈X﹔∗，0〉的一个原子.以L(X)记BCH-代数〈X﹔∗，0〉中所有原子做成的集合，即L(X)={a∈X：若x∈X，x∗a=0，则x=a}.因为0∈L(X)，故L(X)6=Φ.

定义5[4]设〈X﹔∗，0〉是一个BCH-代数，a∈L(X)，记V(a)={x∈X:a∗x=0，即a≤x}，称V(a)为X的一个分支.

定义6[2]设〈X﹔∗，0〉和〈Y﹔λ，0〉是两个BCH-代数，如果存在一个一一映射f:X→Y，使得对于任意的x,y∈X，有f(x∗y)=f(x)λf(y)成立，则称f为X到Y的一个同构映射.

定义7[5]设〈X﹔∗，0〉是一个BCH-代数，若x≤y，即x∗y=0，∀z∈X，有z∗y≤z∗x，则称〈X﹔∗，0〉是一个偏序BCH-代数.

引理1[2]设〈X﹔∗，0〉是一个BCH-代数，Y是X的一个非空子集，则Y是X的子代数的充要条件是Y对运算∗封闭.

引理2[2,4]设〈X﹔∗，0〉是一个BCH-代数，则∀x，y∈X，有下列结论成立：

(1)x∈L(X)⇔0∗(0∗x)=x;(2)[x∗(x∗y)]∗y=0.

引理3[6]设〈X﹔∗，0〉是一个BCH-代数，令B(X)={x∈X:0∗x=0}，则B(X)是X的一个子代数，也是X的一个理想.

由定义5知，B(X)=V(0).

引理4[4]设〈X﹔∗，0〉是一个BCH-代数，则X=∪{V(a):a∈L(X)}(即X=∪

a∈L(X)V(a)).

引理5[4]设〈X﹔∗，0〉是一个BCH-代数，若a,b∈L(X)，且a6=b，则V(a)∩V(b)=Φ.

引理6[1]设〈X﹔∗，0〉是一个BCHK-代数，A是X的一些质子做成的集合，则X−A是X的一个子代数.

引理7[1]设〈X﹔∗，0〉是一个有限偏序BCH-代数，则X一定存在质子.

引理8[5]设〈X﹔∗，0〉是一个偏序BCH-代数，则X中的二元关系≤是一个偏序关系.

2 一般BCH-代数中路径的定义及性质

定义8设〈X﹔∗，0〉是一个BCH-代数，若b是X的一个质子，记U(b)={x∈X:x∗b=0，即x≤b}，称U(b)是由b确定的X的一个路径.

由H-1可知，b∈U(b).

定理1设〈X﹔∗，0〉是一个BCHK-代数，若b是X的一个质子，则U(b)是X的一个子代数.

证明显然b∈U(b).∀x,y∈U(b),则x∗b=0，从而由H-3和BCHK-代数的定义得，(x∗y)∗b=(x∗b)∗y=0∗y=0，这就证明了x∗y∈U(b).根据引理1知，U(b)是X的一个子代数.

定义9设〈X﹔∗，0〉是一个BCH-代数，若A是X的一个非空子集(A可以不是X的子代数)，b∈A，若y∈A，b∗y=0，即b≤y，则y=b，称b是A的一个质子.

由定义2和定义9可以看出，若X的质子属于A，则X的质子一定是A的质子.但反之不一定成立，见下面的例子.

例1设X={0,1,2,3,4}，X中的二元运算∗由下面的乘法表1给出.

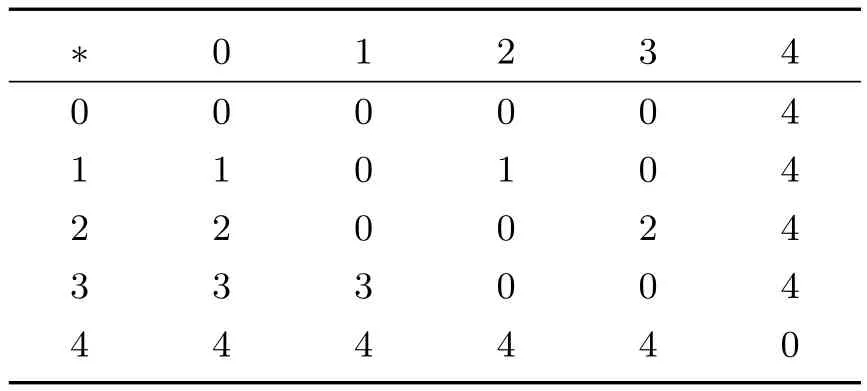
表1 X中的二元运算

可以验证〈X﹔∗，0〉是真BCH-代数(是BCH-代数，但不是BCI-代数).由定义2可知，4是X的唯一质子，且U(4)={4}.设A={0,1,2}⊆X，根据定义9，1是A的质子，但1不是X的质子.又可以看出分支V(0)={0,1,2,3}无质子.

本文不研究BCH-代数的一般非空子集的质子，只研究BCH-代数分支的质子及性质.若一个BCH-代数的某个分支存在质子，则该质子是否是这个BCH-代数的质子呢?下面的定理给出了肯定的回答.

定理2设〈X﹔∗，0〉是一个BCH-代数，a∈L(X)，则有下列结论:

(1)若V(a)存在质子b，则b一定是X的质子;

(2)若V(a)存在质子b，则a∈U(b);

(3)若V(a)存在质子b，则U(b)⊆V(a);

(4)若V(0)存在质子b，则U(b)是V(0)的一个子代数.

证明(1)因b∈V(a)，故a∗b=0;由H-3和H-1得，0∗a=(a∗b)∗a=(a∗a)∗b=0∗b;故0∗a=0∗b.设x∈X，且b∗x=0，同理可得，0∗b=0∗x;因此得，0∗a=0∗x.两端左乘0得，0∗(0∗a)=0∗(0∗x)，由引理2的(1)得，a=0∗(0∗x);两端右乘x并利用引理2的(2)得，a∗x=0，所以有，x∈V(a).又因b是V(a)中的质子，故x=b，这就证明了b也是X中的质子.

(2)因b∈V(a)，故a∗b=0.由定理2的(1)知，b也是X的质子，所以有，a∈U(b).

(3)因b∈V(a)，故a∗b=0.由(1)的证明得，0∗a=0∗b;因b也是X的质子，故∀x∈U(b)，则x∗b=0，同样有，0∗x=0∗b;因此得，0∗a=0∗x.又由(1)的证明得，x∈V(a)，这就证明了U(b)⊆V(a).

(4)由引理3知，V(0)=B(X)是X的一个子代数.因b也是X的质子，故∀x,y∈U(b)，则x∗b=0;由定理2的(3)知，U(b)⊆V(0)，故y∈V(0)，0∗y=0;从而由H-3得，(x∗y)∗b=(x∗b)∗y=0∗y=0，这证明了x∗y∈U(b).根据引理1知，U(b)是V(0)的一个子代数.

由引理4知，若一个BCH-代数X存在质子，则该质子一定属于X的某个分支中.又由定理2的(1)知，若X的某个分支存在质子，则该质子一定是X的质子，从而有下面的推论1.

推论1若一个BCH-代数〈X﹔∗，0〉存在质子，则X的质子做成的集合等于其所有分支的质子做成的集合.

推论2设〈X﹔∗，0〉是一个BCH-代数，a1，a2∈L(X),a16=a2，若V(a1)存在质子b1，V(a2)存在质子b2，则U(b1)∩U(b2)=Φ.

证明由定理2的(3)知，U(b1)⊆V(a1)，U(b2)⊆V(a2);再由引理5知，V(a1)∩V(a2)=Φ;所以有，U(b1)∩U(b2)=Φ.

推论2说明不同分支中质子确定的路径是互不相交的.定理2的(2)说明同一分支中不同质子确定的路径都包含确定该分支的原子，定理2的(3)说明同一分支中不同质子确定的路径都包含在该分支内，因此路径这一概念实质上反映了一个BCH-代数中分支的内部结构.

本节再讨论一下一个BCHK-代数中的特殊质子及性质.

定义10设〈X﹔∗，0〉是一个BCHK-代数，|X|≥2，b∈X且满足:

(1)b是X的一个质子;(2)∀x∈X且x6=b，有x∗b=x，则称b是X的一个不变质子.

例2设X={0,1,2,3,4}，Y={0,1,2,3,4}，X中的二元运算∗与Y中的二元运算λ分别由下面的乘法表给出.

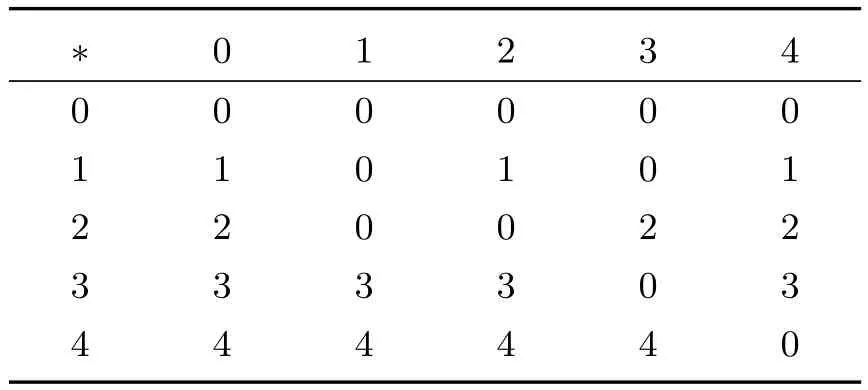
表2 X中的二元运算

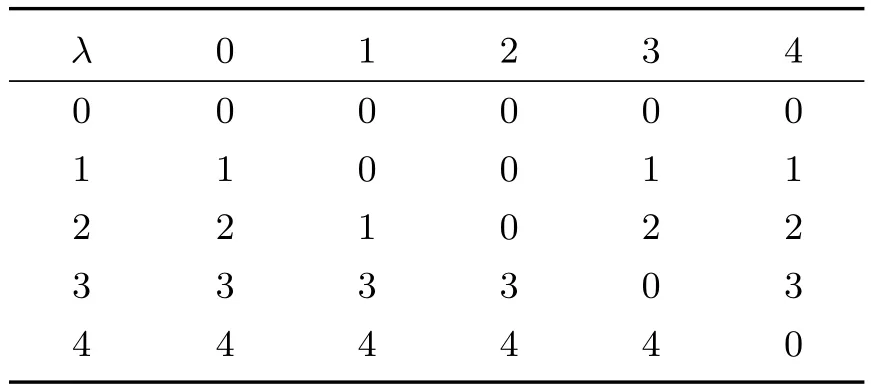
表3 Y中的二元运算

可以验证〈X﹔∗，0〉是一个BCHK-代数(但不是BCI-代数)，3与4都是X的质子，而4是X的不变质子;〈Y﹔λ，0〉是一个BCHK-代数(也是BCK-代数)，2，3，4都是Y的质子，而3与4都是Y的不变质子.

定理3设〈X﹔∗，0〉是一个BCHK-代数，b是X的一个不变质子，则∀y∈X且y 6=b，有b∗y=b.

证明设y∈X且y 6=b. 如果b∗y=z而z 6=b，由H-3，H-1和BCHK-代数的定义得z∗b=(b∗y)∗b=(b∗b)∗y=0∗y=0;因b是X的一个不变质子，故z∗b=z;从而有z=0，进而有b∗y=0.又因b是X的质子，故y=b.这与假设矛盾，所以有b∗y=b.

定理4设〈X﹔∗，0〉是一个BCHK-代数，|X|≥2，a，b是X的两个不变质子，则子代数X−{a}与X−{b}同构.

证明由引理6知，X−{a}与X−{b}都是X的子代数.显然有X−{a}=(X−{a,b})∪{b},X−{b}=(X−{a,b})∪{a}.

定义X−{a}到X−{b}的映射f如下

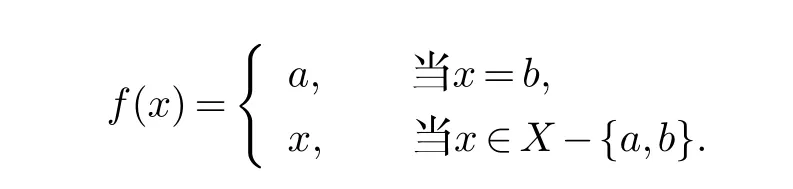
显然f是一个一一映射.下面证明f保持运算，即f(u∗v)=f(u)∗f(v),∀u,v∈X−{a}.为此，分一下四种情形讨论.

(1)当u 6=b，v 6=b时，必有，u∗v 6=b. 因为如果u∗v=b，则由H-3，H-1和BCHK-代数的定义得，b∗u=(u∗v)∗u=(u∗u)∗v=0∗v=0，由b是X的质子推出b=u，这与条件相矛盾.所以根据映射的定义得，f(u∗v)=u∗v=f(u)∗f(v).

(2)当u=b，v 6=b时，因b是X的不变质子，故由定理3得，u∗v=b∗v=b，从而f(u∗v)=f(b)=a;再由a是X的不变质子及v 6=a得，f(u)∗f(v)=f(b)∗v=a∗v=a;所以f(u∗v)=f(u)∗f(v).

(3)当u6=b，v=b时，由b是X的不变质子得，u∗v=u∗b=u，故f(u∗v)=f(u)=u;再由a是X的不变质子及u6=a得，f(u)∗f(v)=u∗f(b)=u∗a=u;所以f(u∗v)=f(u)∗f(v).

(4)当u=v=b时，因为|X|≥2，故0不是BCHK-代数X的质子，当然也不是不变质子，根据映射的定义知，f(0)=0，所以f(b∗b)=f(0)=0=f(b)∗f(b).

综上所述，对∀u,v∈X−{a}，都有f(u∗v)=f(u)∗f(v)成立.所以根据定义6知，子代数X−{a}与X−{b}同构.

3 有限偏序BCH-代数中路径的性质

因为一般的BCH-代数可能存在质子也可能不存在质子，而由引理7知，有限偏序BCH-代数一定存在质子，所以以下无特别说明，总假设〈X﹔∗，0〉是一个有限偏序BCH-代数.由引理8知，〈X，≤〉是由〈X﹔∗，0〉确定的有限偏序集，其中x≤y⇔x∗y=0.按照质子和极大元的定义，X的质子就是有限偏序集〈X，≤〉中的极大元，即在一个有限偏序BCH-代数中质子与极大元是同一概念，以后也就把有限偏序BCH-代数或其非空子集中的质子称为极大元.设A是X的一个非空子集，显然〈X，≤〉也是一个有限偏序集，根据抽象代数的知识，偏序集的任一非空有限子集必有极大元，故〈X，≤〉存在极大元，即A存在质子，用符号M(A)表示A中极大元，即质子做成的集合.

由推论1立即可得下面的定理5.

定理5

定理6设a∈L(X)，则对∀x∈V(a)，∃b∈M(V(a))，使x∈U(b).

证明因x∈V(a)，故a≤x.若x是V(a)的极大元，则x∈U(x)，结论成立.若x不是V(a)的极大元，则∃x1∈V(a)，x16=x，使x≤x1.若x1是V(a)的极大元，则x∈U(x1)，结论成立.若x1不是V(a)的极大元，则∃x2∈V(a)，x26=x1，使x1≤x2，又因x≤x1，由引理8知，x≤x2，同样，若x2是V(a)的极大元，则x∈U(x2)，结论成立.若x2不是V(a)的极大元，重复前面的步骤，由于V(a)是一个有限集，经过有限步之后，一定存在一个极大元xn=b∈V(a)，使x≤x1≤x2≤···≤xn=b，由引理8知，x≤b，所以有，x∈U(b).

定理6说明有限偏序BCH-代数一个分支中的任一元素都包含在该分支中的某个极大元确定的路径内.

定理7设a∈L(X)，则

证明由定理2的(3)知，对∀b∈M(V(a))，由U(b)⊆V(a).故又对∀x∈V(a)，由定理6知，∃b∈M(V(a))，使x∈U(b).故所以有

设a∈L(X)，若V(a)={a}，则a也是V(a)的极大元，由定义8，定理2的(2)和(3)知，U(a)=V(a)={a}，这是路径的一种特殊情形.若V(a),{a}，因V(a)是有限偏序集，故V(a)存在极大元b，使a

定理8

证明对∀x∈X，由引理4知，故∃a∈L(X)，使x∈V(a);再由定理6知，∃b∈M(V(a))，使x∈U(b);而由定理5知，b∈M(X);因此有，显然有，所以得到

设〈X﹔∗，0〉是一个一般的BCH-代数，由引理4知，又由引理5知，若a,b∈L(X)，且a,b，则V(a)∩V(b)=Φ.因此可以把集合X看成一个森林，它是由若干个互不相交的树所组成的.若〈X﹔∗，0〉是一个有限偏序BCH-代数，定理8则说明森林X也可以看成是由所有树枝组成的.

注意定理8对一般的BCH-代数不一定成立.如例2中的表2所确定的BCH-代数〈X﹔∗，0〉(事实上是BCHK-代数)，可以验证〈X﹔∗，0〉不是一个有限偏序BCH-代数.X的全部质子为3与4，而U(3)={0,1,3}，U(4)={0,4}，但U(3)∪U(4)={0,1,3,4},X.

参考文献：

[1]李金龙.BCH-代数的质子[J].新疆大学学报(自然科学版),2017,34(2):158-162.

[2]胡庆平.BCI-代数[M].西安:陕西科学技术出版社,1987.

[3]李金龙,李军.关于BCH-代数导出半群的一些结果[J].安徽大学学报,2015,39(4):1-4.

[4]李金龙.BCH-代数的原子与分支[J].纯粹数学与应用,2003,19(2):145-148.

[5]李金龙.偏序BCH-代数的一种自映射[J].河北大学学报,2006,26(3):242-245.

[6]李金龙.BCH-代数与广义结合BCI-代数的关系[J].汉中师范学院学报,2002,20(2):25-29.