框架剪力墙基础隔震结构地震易损性分析

汤旭，黄慎江

(合肥工业大学 土木与水利工程学院，安徽 合肥 230009)

0 引言

基础隔震技术作为一种被动控制技术，已经广泛应用于多层建筑结构中，并在实际地震中获得了检验，取得了良好的减震效果。随着技术的进步和研究的深入，隔震技术已逐渐向高层领域发展。然而，在地震作用下基础隔震结构也会发生一定损伤。在强震作用下，隔震层可能发生较大的剪切变形而导致承载力下降，上部结构也可能进入非线性阶段。目前，由于基础隔震结构的历史震害资料较少等原因，对该类结构体系在地震作用下的损伤破坏数据记录不多，要深入了解基础隔震结构在地震作用下的损伤状况,比较有效的就是采用理论分析的方法。鉴于此，本文采用一种基于性能的地震易损性分析方法，可以准确、全面的反应结构在不同地震动强度下的损伤状况。

易损性研究的发展史可追溯到20世纪70年代，国内外对结构易损性做了大量的研究，并取得了丰富的成果。Hwang等[1]分别以普通钢筋混凝土结构、平板结构以及钢框架结构为对象，对三种类型的结构进行了地震易损性分析。Kircil等[2]以钢筋混凝土框架结构为研究对象，选取12条人工地震波，采用IDA方法分别对3层、5层和7层三种结构进行分析，由此得到三种结构的地震易损性曲线，分析了结构层数对地震易损性的影响。吕大刚和王光远等[3]将结构的地震易损性分析问题转化为结构的抗震可靠度问题进行求解，提出了采用有限元可靠度方法对结构进行易损性分析的新方法。韩淼等人[4-5]采用增量动力法和能力谱法求得了结构在罕遇地震下的最大层间位移角，将最大层间位移角作为整体性能指标，对结构进行了地震易损性分析，给出了结构失效概率和水平地震加速度峰值的函数关系式，计算出不同设防烈度的剪力墙结构在罕遇地震下的震害矩阵。本文首先介绍了易损性分析方法，进而定义了基础隔震结构的4个性能水准，通过对框架剪力墙基础隔震结构进行易损性分析，得到了该类结构的破坏概率和易损性曲线，从而为该类结构损伤评估提供依据。

1 易损性及分析方法

地震易损性是指结构在某种地震强度作用下超越某种极限破坏状态的条件概率。地震易损性从宏观上描述了地震动强度与结构破坏程度两者之间的关系，从概率的角度定量地描述了结构的抗震性能。通过对结构进行易损性分析，可以得知结构在不同等级地震下的破坏概率。在进行易损性分析时，首先建立结构的有限元模型，根据现有的震害资料，选取合理的地震动参数，输入到有限元模型中进行非线性动力时程分析，根据模型易损性分析结果对结构的抗震性能进行研究。图1为本文的易损性分析方法。

图1 易损性分析方法

2 性能水准的确定

性能水准是指结构在可能遇到的特定设计地震作用下所容许的极限破坏[6]。基于性能的设计方法与结构易损性研究有着密切的联系，性能水准的划分反复出现在各类抗震规范中。美国的ACT-40将结构的性能水准划分为立即居住、损伤控制、生命安全和结构稳定4个等级[7]，日本将结构的性能水准划分为安全性、适用性和破坏控制3个等级[8]，刘鹏飞等[9]将基础隔震结构划分为第一水准、第二水准和第三水准3个等级，并且对每个性能水准的特征做了详细的描述。本文根据我国规范条文规定及前人的研究成果，将基础隔震结构的性能水准划分为正常使用状态(NO)、立即使用状态(IO)、生命安全状态(LS)和防止倒塌状态(CP)4个不同极限状态。根据上部结构在地震作用下的损伤状况，将基础隔震结构划分为5个破坏状态：基本完好、轻微破坏、中等破坏、严重破坏以及倒塌[10]。表1给出了结构的性能水准及特征。

将性能水准划分后需要对性能水准量化，确定出结构不同性能水准的极限状态点。性能水准是根据结构在地震作用下的损伤程度定义，而损伤程度通过结构的损伤参数来描述。目前，主要采用层间位移或层间位移角作为作为结构损伤评价参数，这两个指标在易损性的评价过程中同时具备兼容性和有效性，美国的HAZUS99系列损伤评估准则就选取了这一参数作为评定结构地震易损性的指标。本文使用上部结构的最大层间位移角作为结构损伤评价参数。参照 《建筑抗震设计规范》(GB50011-2010)并结合大量实验和震害统计资料，定义了结构不同性能水准对应的量化指标限值见表2，表3给出了不同破坏状态与量化指标之间的关系。

表1 结构性能水准

表2 量化指标限值

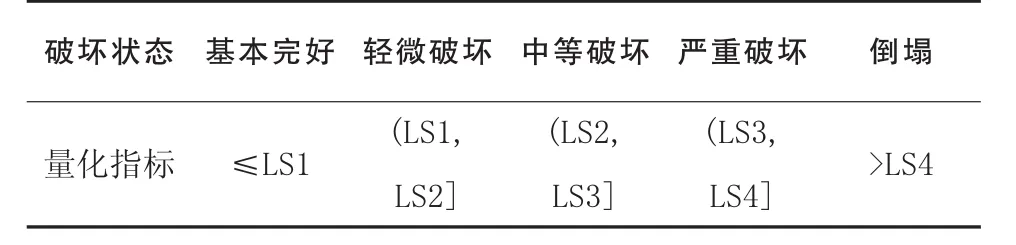
表3 不同破坏状态与量化指标关系

3 模型的建立

3.1 模型概况

本文以一个十二层钢筋混凝土框架剪力墙结构为例进行仿真分析。其标准层层高为3.3 m，总高度为36.3 m；1～6层柱截面尺寸为700 mm×700 mm，7～12层为650 mm×650 mm；框架梁截面尺寸为250 mm×650 mm；剪力墙厚度为250 mm；楼面板厚度为120 mm。柱、剪力墙混凝土强度等级为C35，梁混凝土强度等级为C30。建筑抗震设防类别为丙类，抗震等级为框架三级、剪力墙二级，抗震设防烈度为8度，设计地震加速度为0.20 g，场地类别为Ⅱ类，设计地震分组为第一组。各层均布恒荷载为3.0 kN/m2，均布活荷载为2.0 kN/m2。图2给出了结构的平面布置图。

图2 结构平面布置

3.2 隔震支座的选型与布置

按照 《建筑抗震设计规范》 (GB 50011-2010)第12.2.3条中丙类建筑隔震支座平均压应力限值应小于等于15 MPa的规定[11]，由上部结构计算出的柱底和底层荷载分配给每个支座上的竖向力，得出每个支座上的轴向力初步确定每个支座的直径及数量。根据规范要求与支座选择原则，经过反复计算，择优选取某公司生产的3种类型的铅芯隔震支座：GZY600-120、GZY700-140、GZY900-180。表4给出了隔震支座的性能参数。

表4 隔震支座的性能参数

4 易损性分析

4.1 地震波的选取

地震动主要受震源、场地条件和震中距等因素的影响，具有较大的随机性。因此，对结构进行时程分析时，选取的地震动不同，可能会造成结构的响应有很大的差异。为了减小由地震动记录不同带来的这种差异，合理地选取地震动记录非常关键。根据Luco和Cornell的研究，对于中高层建筑选取10～20条地震波即能减少这种差异[12]。根据工程资料，从太平洋地震工程研究中心数据库选取13条断层距小于20 km、震级在6.5～7.0之间的近场地震动来进行本文的易损性分析，选取的地震动加速度反应谱如图3所示。

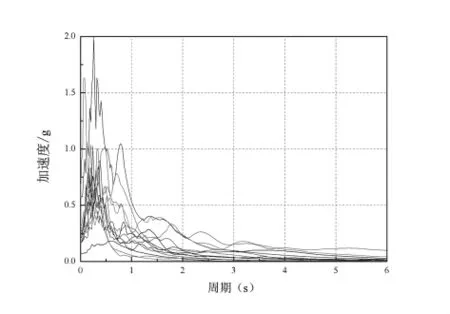
图3 地震动加速度反应谱

4.2 结构的概率需求分析

概率需求分析是指在特定地震动强度下，结构地震响应的概率计算。将每一条地震波的峰值加速度按比例进行调幅，调幅比例为0.1 g、0.2 g、0.4 g、0.6 g、0.8 g、1.0 g、1.2 g、1.4 g、1.6 g、1.8 g及2.0 g，对结构进行非线性动力时程分析。这样得到了以峰值加速度为变量的上部结构最大层间位移角数据。将结构响应按照性能水准进行划分，得到了结构损伤数据如图4所示。图4中共143个数据点，每个点均代表动力时程分析时基础隔震结构的响应，每列竖向数据点为相同峰值加速度(PGA)下的上部结构最大层间位移角，水平线LS1～LS4为不同性能水准限值，其取值与表2中量化指标限值相对应。从上图中可以看出，当PGA＜0.6g时，相同PGA地震波作用下结构的最大层间位移角离散性很小；当PGA＞0.6g，随着PGA的增大，结构最大层间位移角的离散性逐渐增大。

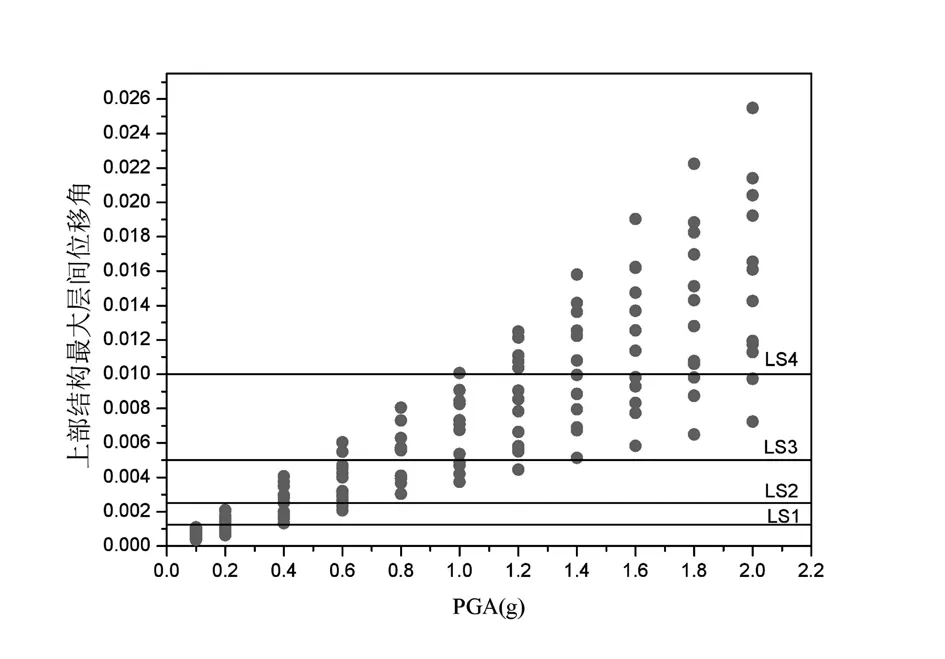
图4 上部结构最大层间位移角与PGA的关系

假设相同PGA下上部结构的最大层间位移角满足对数正态分布，则可以用对数正态分布函数来表示结构的地震需求u的概率密度函数，即为：

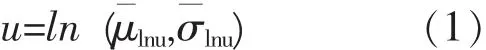
式中μlnu,σlnu为结构需求的对数均值和对数方差。

利用MATLAB软件对上述数据进行处理分析，绘制对数概率密度函数如图5。图5给出了PGA为0.4 g、0.8 g和1.4 g时结构的对数概率密度函数。从图中可以看出，当PGA为0.4 g时，结构的地震反应大部分集中在LS1～LS3之间，说明结构处于轻微破坏或中等破坏状态。当PGA为0.8 g时，结构的地震反应集中在LS2～LS4之间，说明结构处于严重破坏的状态。当PGA为1.4 g时，结构的地震反应大部分集中在LS3～LS4之间，说明结构已经进入了倒塌阶段。对比图4和图5可以看出，当PGA为0.4 g、0.8 g和1.4 g时，两者的结构地震反应的数据点集中区域是一致的。

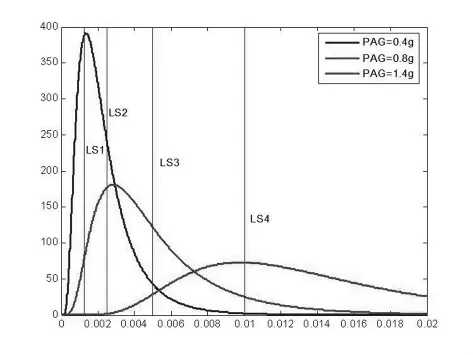
图5 对数概率密度函数

4.3 结构的易损性分析

结构易损性分析从宏观上描述了地震动强度与结构破坏程度之间的联系，可以得知结构在不同等级地震动强度下的破坏概率，从概率的角度定量地描述了结构的抗震性能。根据本文对于结构性能水准的定义和结构的概率需求分布，不同PGA下的结构需求超越各个性能水准的概率的表达式为：

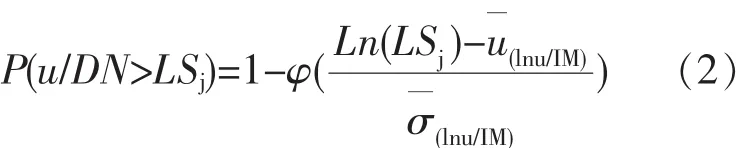
式中DM为结构损伤参数，本文用结构的最大层间位移角表示，是指在特定的地震动强度PGA下结构需求的对数均值和对数方差，LSj表示4个性能水准的量化指标限值。根据不同性能水准的量化指标限值，基于上述求解公式，便可以求解出结构在特定峰值加速度PGA下各性能水准的失效概率，进而得到结构的易损性曲线，如图6所示。

图6中横坐标表示地震峰值加速度用PGA表示，纵坐标表示超越概率P。不同的曲线表示不同的性能水准，4条曲线将图形划分为基本完好、轻微破坏、中等破坏、严重破坏和倒塌5个区域。从图中易损性曲线的特征可以看出，正常使用极限状态曲线走势相对其他3条曲线走势较陡，说明结构在地震作用下保持正常使用状态而不发生破坏的概率较小，即结构比较容易达到抗震规范所规定的弹性范围。随着结构损伤程度的加深，立即使用状态、生命安全状态和防止倒塌状态的易损性曲线走势逐渐趋于平缓，说明随着地震动峰值加速度的增大，结构逐渐超越弹性变形阶段进入塑性变形阶段，表现出良好的抗震性能。当PGA=0.4 g时，即在罕遇地震下，基础隔震结构进入正常使用状态的概率为87%，进入立即使用状态的概率为28%，进入生命安全状态的概率为1.4%，进入防止倒塌状态的概率为0，说明基础隔震结构在罕遇地震作用下，还处于轻微破坏或中等破坏状态，发生严重破坏概率很小。

图6 地震易损性曲线

5 结论

本文系统的介绍了框架剪力墙基础隔震结构基于性能的易损性分析方法，首先建立了合理的结构-地震模型，结合基础隔震结构的极限破坏准则对模型的地震易损性进行了分析，最后绘制出地震易损性曲线，由此得到以下结论。

(1)基础隔震结构在设防地震下，处于正常使用状态；在罕遇地震下，主要处于轻微破坏或中等破坏状态，表现出了良好的抗震性能，起到了很好的隔震作用。

(2)得到了框架剪力墙基础隔震结构的地震易损性曲线，不仅可以准确、直观地评价基础隔震结构在不同强度地震作用下可能发生的破坏形态，而且可以对该类结构的抗震性能进行评估，为该类结构的震前灾害预测和震后损失评估提供依据。

(3)本文只进行了Y向地震作用下的地震分析，并不能反应真实的地震反应情况，对于双向地震作用下结构的反应有待进一步研究。同时本文只考虑了上部结构的损伤，对隔震支座部分的损伤也有待进一步研究。

[1]Hwang H H M,Low Y K,Hsu H M.Seismic reliability analysis of flat-plate structures[J].Journal of Engineering Mechanics,1990,5(1)：2-8.

[2]Kircil M S,Polat Z.Fragility analysis of mid-rise R/C frame buildings[J].Engineering Structures,2006,28(9)：1335-1345.

[3]吕大刚,王光远.基于可靠度和灵敏度的结构局部地震易损性分析[J].自然灾害学报,2006,15(4)：157-162.

[4]韩淼,那国坤.基于增量动力法的剪力墙结构地震易损性分析[J].世界地震工程,2011,27(03)：108-113.

[5]韩淼，李守静.基于能力谱法的框架-剪力墙结构地震易损性分析[J].土木工程学报，2010，43(S1)：108-112.

[6]Vision 2000 Committee.Performance Based Engineering of Building[P].Miranda E.Seismology Commit-tee of the Structure Engineer Association of Californ-ia，Oak-land： Wiley Inc，1995.

[7]ATC-40.Seismic Evaluation and Retrofit of ConcreteBuilding[S].Applied Technology Council.Red Wood City,California，1996.

[8]小谷俊介，叶列平.日本基于性能结构抗震设计方法的发展[J].建筑结构，2000(06)：3-9+58.

[9]刘鹏飞，刘伟庆，王曙光.基础隔震结构的性能水准与设防目标[J].工程抗震与加固改造,2008,30(06)：55-59.

[10]杜永峰，王光环.基础隔震钢筋混凝土框架结构的性能水准划分与量化分析[J].工程抗震与加固改造，2013，35(06)：87-92+97.

[11]中国建筑科学研究院.建筑抗震设计规范：GB50011-2010[S].北京：中国建筑工业出版社，2016.

[12]Luco.N,Cornell.C.A.Effects of connection fractures on SMRFseismic drift demands[J].Jou-rnal of Structural Engineering,2000,126(1)：127－136.