乡村自驾旅游线路优化及实现

樊丹 张美琳

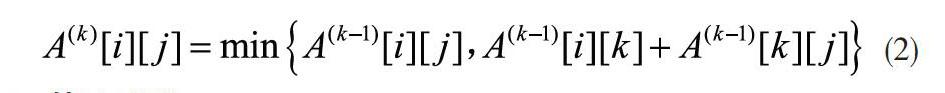
[摘 要]对于乡村自驾旅游者而言，合理优化后的旅游线路不仅可以减少旅游者的经济与时间成本，同时也可体现其个性化的需求。文章对经典的Floyd算法进行改进，综合考虑交通费用、景点间距离等因素，最终确立了成都周边乡村自驾旅游的最优方案;为使优化后的线路更加智能化，构建了基于高德地图API的旅游线路可视化系统，此可视化系统能够智能化地推送给旅游者最优化的旅游线路，极大改善其旅游体验，为自驾旅游者的出行提供有价值的参考与借鉴。

[关键词]Floyd算法;乡村旅游;线路优化;地图API

[中图分类号]F592 [文献标识码]A

1 引言

随着人民生活水平的不断提高，居民私家车的持有量在逐年攀升，张扬个性与休闲体验结合的“乡村自驾旅游”已然成为一种时尚的旅游方式，并由此催生了乡村旅游的发展与壮大，其相关理论研究也开始受到学者们的关注。史春云通过对自驾游客满意度进行实证研究后得出，自驾旅游最主要的限制因素不在目的地或者交通方面，而是体现在出行成本高等方面。栾玲提出旅游线路设计应节省游客时间、路程、费用，并使景点内容丰富，避免重复经过相同旅游点，线路编排应劳逸结合、富有节奏感。目前，针对自驾旅游线路的设计，学者们普遍从乡村旅游资源开发、自驾旅游消费行为等角度对自驾旅游线路进行整合，较少涉及运用优化算法对自驾旅游线路进行设计。

2 问题提出

设计最优自驾旅游线路的问题，可通过简化构建为连接各旅游目的地的TSP旅行商问题模型，即寻找到一条路径遍历所有的节点，使路径总长度或总费用之和达到最小值。Floyd算法作为求解TSP旅行商问题的经典方法，是研究和解决旅游交通中线路优化的首选算法，因此本文以成都市周边乡村自驾旅游为例，综合考虑出行费用、景点间距离等方面的因素，运用改进的Floyd算法对优质乡村旅游景点进行整合，设计出串联多景点的乡村自驾旅游线路，并采用高德地图API将优化后的自驾旅游线路进行动态实现与展示，为自驾旅游者出行线路的选择方面提供借鉴与参考。

3 算法介绍及改进

3.1 Floyd算法思想

Floyd（弗洛伊德）算法也可称其为插点算法，是一种运用逐步逼近和递推的思想来寻求给定加权图中多节点之间最短路径的算法。Floyd 算法的基本思想是：对一个顶点个数为n的有向网（或无向网），设置一个n×n的方阵A（k），其中除对角线的矩阵元素等于0以外，其他元素A（k）[i][j]（i≠j）表示从顶点vi到顶点vj的有向路径长度，依次插入顶点构造出n阶方阵序列A（-1）， A（0）， A（1）， A（2）…A（n-1），从而形成图的距离矩阵A（n-1），最终求得任意两点间最短路径。其中A（k）的元素A（k）[i][j]的递推公式如式（1）、（2）所示：

3.2 算法改进

由于经典的Floyd算法是计算多个节点间的最短路径，在输入初始矩阵进行封装时，随着节点个数的增加，势必会出现输入过程越发繁琐的情况。因此针对邻接矩阵的结构特点，对经典Floyd算法进行输入矩阵的改进，以此来提高算法的实用性。改进Floyd算法的核心代码如下：

Step 1： 确认顶点个数;

function Floyd（ ）

int ARow ， ACol;

printf（"输入矩阵的行数和列数：＼n"）;

scanf（“%d，%d”，&ARow，&ACol）;

arr=new double *[ARow];

for（i=0;i<=ARow;i++）

arr[i]=new double[ACol];

Step 2： 输入顶点间的距离，得到初始矩阵;

printf（"输入二维矩阵的数据（%d行%d列）：＼n"，ARow，ACol）;

for（i=0;i

for（j=0;j

scanf（“%f，”，&tmp）;

arr[i][j]=tmp;

Edge[i][j]=arr[i][j];

dist[i][j]=Edge[i][j];

if（ i！=j && dist[i][j]

else path[i][j]=-1;

Step 3：依據封装好的初始矩阵进行标准Floyd运算，依次输出各节点序号，得出各节点间的最短路径。

4 算法在自驾旅游线路优化中的应用

4.1 案例背景

党的十九大报告在实施“乡村振兴战略”中提出“发展多种形式适度规模经营，培育新型农业经营主体，健全农业社会化服务体系，实现小农户和现代农业发展有机衔接”。成都作为“中国农家乐旅游发源地”城市，发展势头迅猛，仅2018年一季度成都市乡村旅游接待总人次超过2500万人次，同比增长达7%;实现乡村旅游总收入超过75亿元，同比增长达20%。乡村旅游已成为成都市落实乡村振兴战略中的重要力量、重要途径和重要引擎。

为使研究样本具有代表性，本文选取成都周边深受自驾车游客喜爱的8个乡村旅游景点进行分析，这8个景点分别是：茶溪谷、妈妈农庄、烟霞湖风景区、长滩湖湿地、仁康庄园、宝山旅游度假区、桃花故里、三溪白庙村，并将其依次标记为Ci（i=1，2，…8）。

4.2 研究假设及数据来源

4.2.1 研究假设。假设乡村自驾旅游是以私家车为交通工具，路况通畅，天气等一切突发情况不纳入考虑范围。由于交通费用与燃油费及公路等级有关，本文依据四川省收费标准进行假设：燃油费0.65元/车·公里，京昆、夏蓉、蓉昌等高速公路0.45元/车·公里，成都绕城高速0.57元/车·公里。

4.2.2 数据来源。利用高德地图API提供的经纬度信息及研究假设，得到8个节点构成的距离邻接矩阵与交通费用权值表，如表1、表2所示。

4.3 实验结果

4.3.1 线路优化结果。通过改进的Floyd算法对优选的8个乡村自驾旅游景点进行经纬度、距离及费用等数据的运算操作，得出优化前后的乡村自驾旅游路径图如图1、图2所示。

4.3.2 最优乡村自驾旅游线路。本文因采用矩阵输入路径的优势，综合考虑景点间距离及交通费用等方面因素，得到从不同景点出发的最优路线，如表3所示。

4.4 高德地图API前台实现

高德地图API（Application Programming Interface）是一种使用JavaScript等开发语言编写的应用程序接口，它能够帮助程序员在网站中构建功能丰富、交互性强的个性化地图应用程序。为使自驾车旅游者能够更加智能化地获取到最优旅游路线等相关信息，本文在高德地图 API的基础上，结合HTML及JavaScript进行前端界面设计，实现了包含动画全览、测距等功能的旅游线路可视化系统。

amap.com/lbs/static/addToolbar.js”>，并采用marker、moving与AMap. addDomListener实现添加标注与动画功能，实现结果如图3所示。

4.4.2 测距功能。使用鼠标在地图上绘制任意的折线，结束后便可测量出起止间的距离，如图4所示。

5 结论

为应对乡村自驾旅游者在旅游线路规划方面的个性化需求，本文对经典的Floyd算法进行输入矩阵的改进，并将其運用到自驾车旅游线路的优化中，得出成都周边乡村自驾旅游最优方案，设计并实现了基于高德地图API的旅游线路可视化系统，此系统既为乡村自驾旅游者量身定做、适需对路的优化旅游路线，节约游客时间和经济成本，极大改善其旅游体验，提升自驾旅游的乐趣。旅游线路优化算法的运用与可视化系统的实现，以智能化的方式完善了乡村旅游业的路线开发水平，对于推动乡村旅游业的发展具有较深远的意义。

[参考文献]

[1] 谢雨萍，罗敏.基于“三位一体”方法论的桂北生态农业旅游线路设计[J].特区经济，2009（10）.

[2] 马思斯，李玲，刘庆友.江苏乡村旅游落地自驾消费需求的调查[J].旅游管理研究，2018（06）.

[3] 史春云，孙勇，张宏磊，等.基于结构方程模型的自驾游客满意度研究[J].地理研究，2014（04）.

[4] 栾玲.探析国内旅游线路设计[J].现代商业，2016（03）.

[5] 王桂平，王衍，任嘉辰.图论算法理论、实现及其应用[M].北京大学出版社，2011.

[6] 习近平.决胜全面建成小康社会，夺取新时代中国特色社会主义伟大胜利——在中国共产党第十九次全国代表大会上的报告[M].北京：人民出版社，2017.

[7] 蒲姝.我国乡村旅游发展现状与对策研究——以成都市乡村旅游为例[J].生态经济，2010（05）.

[8] 梁光荣，黎红.百度、高德及Google地图API的比较研究[J].软件导刊，2017（09）.