Tidal Forces in Dyonic Reissner-Nördstrom Black Hole

M.Sharif and Lubna Kousar

Department of Mathematics,University of the Punjab,Quaid-e-Azam Campus,Lahore-54590,Pakistan

1 Introduction

One of the crucial developments on the landscape of astrophysics is the detection of black holes(BHs)as well as mysteries behind its origin.Our modern perspective for conclusive evidences of BHs introduces a new vision of tidal effects around them.The study of BHs has been a subject of interest for scienti fic community and researchers since many years for a variety of reasons.The fascinating nature of BHs makes them curious exotic entities of the universe.It is widely accepted that BHs are formed as a result of gravitational collapse of a massive star.[1]Recent developments assure that BHs exhibit a strong gravitational pull such that nothing can escape from its gravitational field not even a light ray.Due to this alluring feature,the interior region of BH cannot be observed directly by an external observer as it is enveloped by an event horizon(a point of no return).Black holes being high curvature regions can never be destroyed by the external fields.

Any state of matter that enters into a BH encounters a change in its mass,charge and angular momentum.It is well-known that BHs pull everything towards them instead of throwing it out.[2]Its internal information can be studied by investigating the geodesics around them.Geodesics are crucial to investigate physical significance of a given spacetime as they provide considerable insights to analyze the internal structure of BHs.There exists a variety of BHs depending upon their characterizing parameters.Schwarzschild BH(uncharged)is the simplest one having only mass parameter while Reissner-Nordström(RN)(electrically charged)and Kerr(rotating)BHs contain some more parameters.Later on,regular,tidal charged,dyonic BHs etc.have been presented.

The no-hair theorem[3]of classical general relativity states that stationary BHs could be characterized by three parameters,i.e.,mass,charge and angular momentum.The RN spacetime described by mass as well as electric charge possesses a horizon and therefore describes a BH ifIf this inequality is not satis fied then the metric describes a naked singularity.Black holes also possess a magnetic charge if such existed.A particle with electric and magnetic charge is called a dyon and a BH having dyon is termed as dyonic BH.This BH is of special interest as it allows one to study spherical con figurations with magnetic charge.[4]The interest in the possibility of dyonic BHs has grown since magnetic monopoles have been predicted in various extensions of the standard model of particle physics.The metric of dyonic RN BH is identical to RN BH with replacement

It is well-known that magnetic monopoles present in grand uni fication theories give rise to dyonic BHs.[5]Stuchlik[6]investigated motion of charged particles near dyonic Kerr-Newmann de Sitter spacetime.Semiz[7]found the validity of cosmic censorship conjecture near dyonic BHs.Virbhadra and Parikh[8]discussed BH characterized by scalar,electric and magnetic charges having curvature singularity atr=0 similar to RN BH.Ghosh and Mitra[9]studied entropy of dyonic BH in extremal case and found its dependance on mass or charge rather than its area.Sharif and Iftikhar[10]explored neutral as well as charged particle dynamics in the vicinity of dyonic RN BH and concluded that both electric and magnetic charges strongly in fl uence the particles moving around this BH.These studies motivated researchers to consider dyonic BHs for their astrophysical rami fication.

Many surveys have been done for the extensive description of tidal forces near BHs.Mashnoon and Theiss[11]studied relativistic tidal forces for a rotating system and provided a technique for their measurement.Kosti´cet al.[12]made a theoretical survey for the tidal effects near massive BHs and found tidal effects too intense to melt highly massive solid objects in the vicinity of BH.Britoet al.[13]investigated tidal effects in higher-dimensional BH and pointed out that more energy can be extracted from BH in case of higher dimensions. Fuchs[14]proposed a general formalism for the solution of geodesic deviation equations for static spherically symmetric spacetimes.Ba˙za´nski and Jaranowski[15]discussed a solution of geodesic deviation equations for Schwarzschild BH.

This paper is devoted to investigate the effects of magnetic charge on tidal forces in the vicinity of dyonic RN BH.The format of the paper is as follows.In next section,we introduce the metric of dyonic RN BH and discuss Newtonian radial acceleration.Section 3 deals with radial as well angular tidal forces for this BH.We determine the analytical solutions of geodesic deviation equations in Sec.4.Finally,we summarize the results in the last section.

2 Dyonic Reissner-Nordström Black Hole

In this section,we study the effects of magnetic charge on tidal forces for dyonic RN BH.The line element for this BH is given by

In Newtonian mechanics,the radial acceleration is de fined asUsing Eq.(5),we obtain the corresponding acceleration as

which is the radial acceleration that affects the motion of a neutral freely falling test particle.Equation(8)involves the termwhich purely represents the relativistic effect.The particle that falls atwould return back atRstopand can be determined readily as a root ofE2−g(r)

3 Tidal Forces

In this section,we investigate tidal forces in the vicinity of dyonic RN BH.We consider a sphere consisting of two(non-interacting)particles falling towards the center of earth.Since particles near the earth will move faster due to its strong gravitational attraction,so the sphere does not retain its shape and becomes an ellipsoid.Likewise,a body falling towards any spherical region encounters distortion in it but for BHs this effect becomes in finite due to singularity.Therefore,a body near BH experiences in finite stretching and compression in it.

The geodesic deviation equation develops a relation between any two closed freely falling test particles and curvature by the following[18−19]

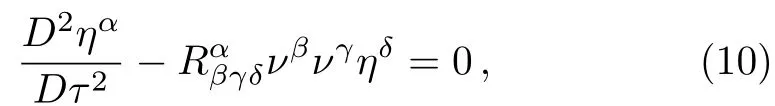
whereηαandνγrepresent geodesic deviation vector and unit tangent vector of the geodesic,respectively.

The Jacobi field is a vector field along a geodesic,which provides the difference between geodesic and an in finitesimally close geodesic.In order to explore the behavior of Jacobi fields,we de fine tetrad basis for freely falling test particles in the radial direction as hereThe corresponding non-zero components of Riemann curvature tensor are

3.1 Radial Tidal Force

Here,we discuss tidal force in the radial direction.Using Eqs.(2)and(14),the radial tidal force becomes zero

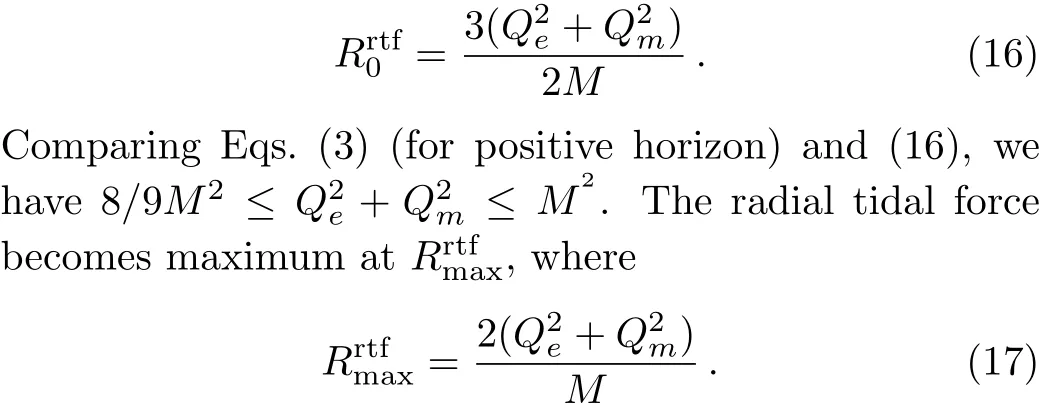
Figure 1 shows the behavior of radial tidal force in terms of radiusr/Mfor different values of magnetic charge.It is noted that radial tidal force always exhibits a local maximum.We observe that tidal force remains positive for Schwarzschild case whereas in finite stretching of a body takes place near the singularity as expected while stretching of a body reduces for RN BH which further reduces for dyonic RN BH.The radial tidal force becomes minimum in the presence of magnetic charge,which shows that body will be stretched less for the dyonic RN BH as compared to Schwarzschild and RN BH.The plots show similar behavior for different values ofb.Thus we have takenb=100 M throughout the paper.

Fig.1 (Color online)Plots for radial tidal force corresponding to different values of magnetic charge with b=100M.

3.2 Angular Tidal Force

Here we examine tidal force in the angular direction.Using Eqs.(2)and(15),we find that the tidal force in the angular direction vanishes atgiven by

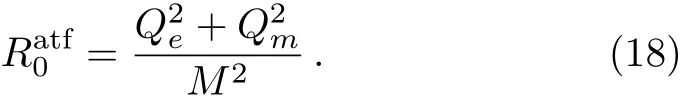
Using Eqs.(2)and(18),we obtainimplies that angular tidal force vanishes at any point in the event and Cauchy horizons,while the equality holds for extremal dyonic RN BH.Figure 2 shows the behavior of angular tidal force in terms of radius for particular values of magnetic charge.We observe that angular tidal force is minimum for smaller values of magnetic charge,i.e.,in finite compression of a body takes place in the angular direction.Thus the body will be compressed less for dyonic RN BH as compared to Schwarzschild case.

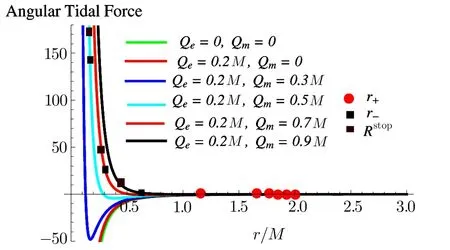
Fig.2 (Color online)Plots for angular tidal force corresponding to different values of magnetic charge with b=100M.

4 Geodesic Deviation Equations

In this section,we evaluate geodesic deviation vectors to understand the stretching or compressing behavior of freely falling test particles around dyonic RN BH.The geodesic deviation equations provide relativistic acceleration between freely falling test particles in a gravitational field.The exact solution of these equations provide a better understanding of the nature of separation between geodesics.[22]For this purpose,we solve Eqs.(14)and(15)through Eq.(5)such that

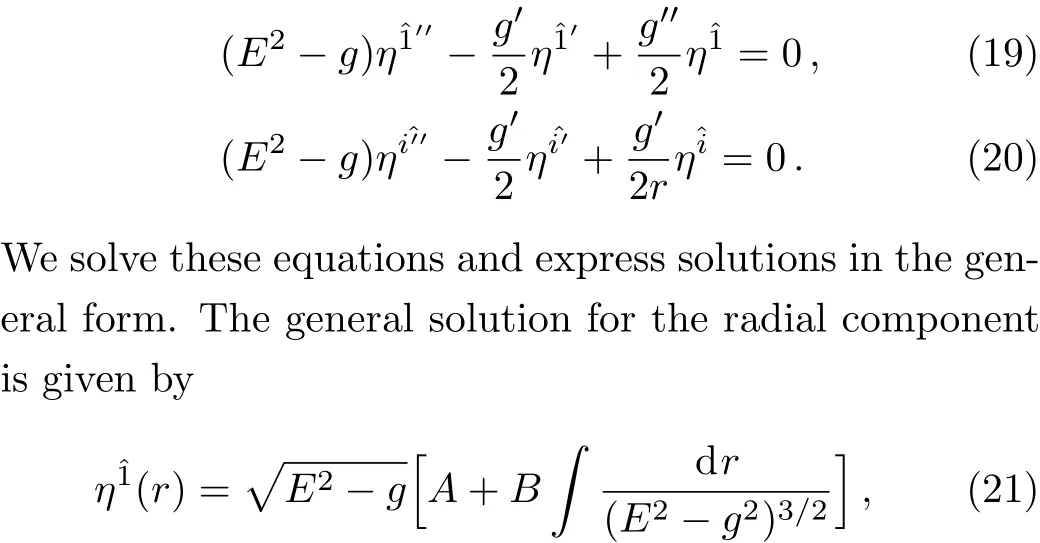
while the respective solution for angular component is

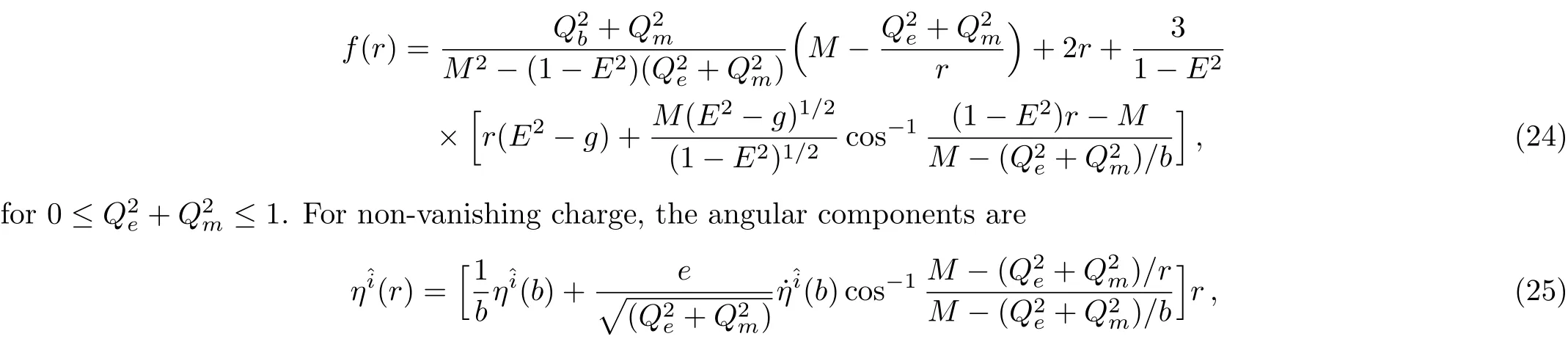
which,for uncharged case,reduces to

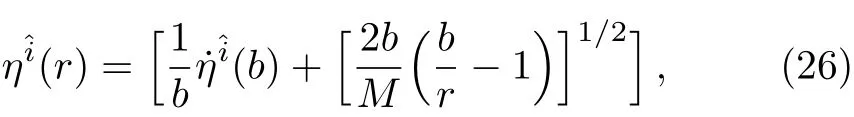
whereandrepresent angular and radial geodesic deviation components,respectively atr=bwhiledenote the respective derivatives corresponding toτ.

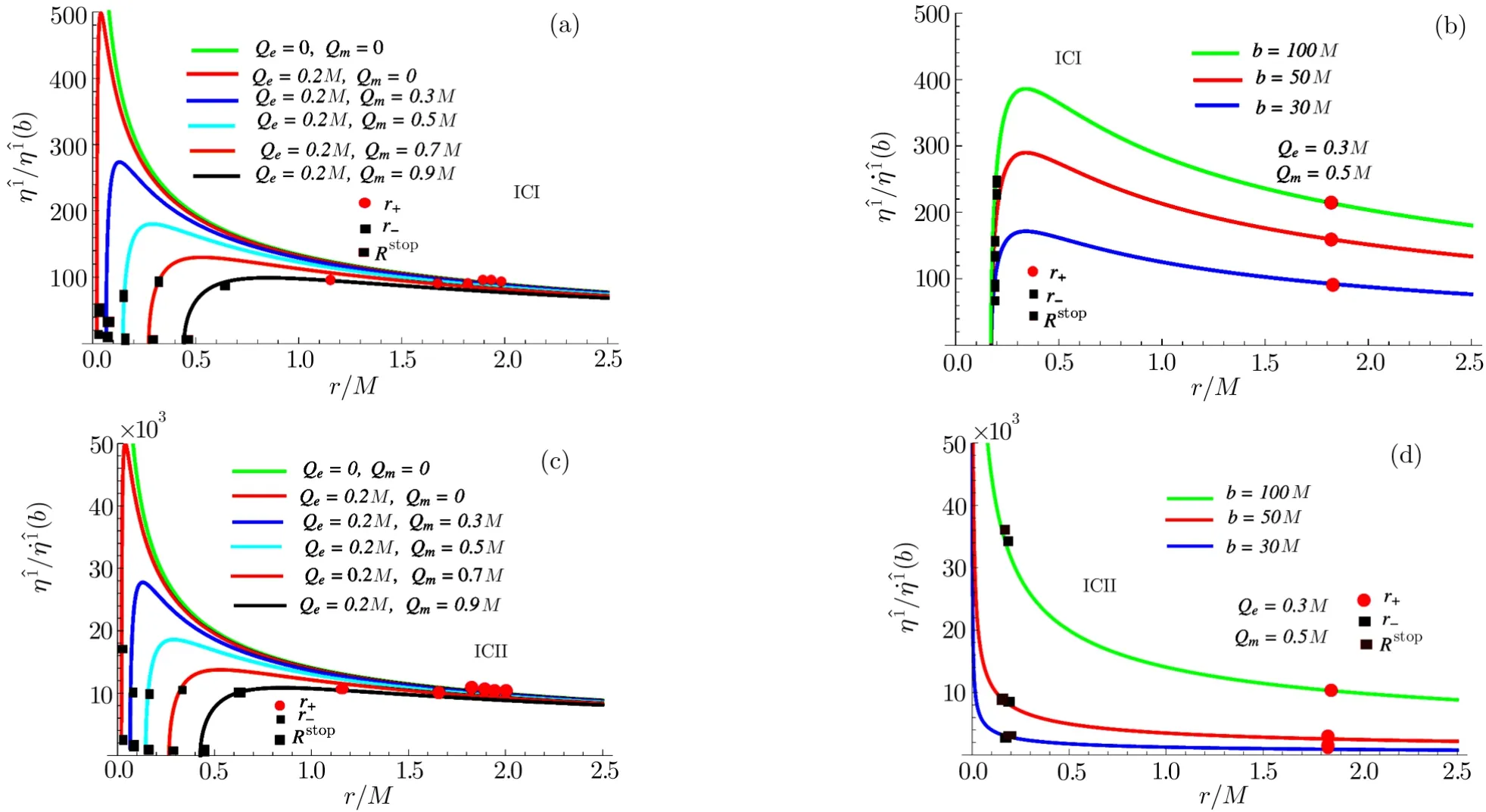
Fig.3 (Color online)Plots for radial components of geodesic deviation vector corresponding to b=100M with different choices of magnetic charge(a)(c)and for different values of b with Qe=0.3M,Qm=0.5M(b)(d).

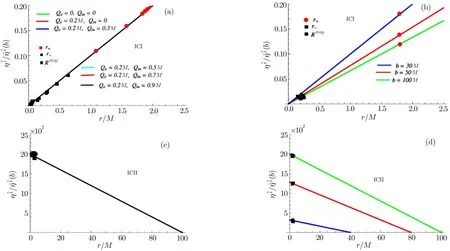
Fig.4 (Color online)Plots for geodesic deviation components in the angular direction for different choices of magnetic charge for b=100M(a)(c)with different values of b and Qe=0.3M,Qm=0.5M(b)(d).

Figure 3 represents the plots for radial geodesic component in terms of radiusr/M.Figures 3(a)–3(b)correspond to ICI whereas Figs.3(c)–3(d)correspond to ICII.Here ICI and ICII represent two different initial conditions for radial and angular geodesic deviation components atr=b.For ICI,we choose=b.For ICII,we take=b.The initial condition ICI represents a body at rest,i.e.,there will be no internal motion whereas the condition ICII represents a body releasing fromr=b.

For ICII,the radial component always increases for a body that falls freely fromr=btor+.For the charged case,during the radial infall of a body fromr=r+tor=r−,the geodesic components in the radial direction tend to increase,attain its maximum then decrease until it reachesr−.During the radial infall of a body betweenr−andRstop,the corresponding radial components continue to decrease and ultimately reduce to zero atRstop.The radial geodesic component with condition ICI behaves identical to ICII except for.Figure 4 shows the plots for angular geodesic components in terms of radiusr/M.For ICII,we find that the angular components decrease for the increasing values ofr/Mindicating their compressing nature.In case of ICI,the angular geodesic components decease linearly inr.This is true since all the geodesics having zero angular velocity trace straight radial lines.

5 Final Remarks

In this paper,we have explored the effects of magnetic charge on tidal forces in the context of dyonic RN BH.We have evaluated Newtonian radial acceleration using radial geodesics and radial as well as angular tidal force components using geodesic deviation equation.We have studied solutions of the geodesic deviation equations.The results are summarized as follows.

It is found that tidal force depend upon charge-to-mass ratio of dyonic RN BH.We have also found that the tidal effects near charged and uncharged BHs are quite different from the effects near the horizon of BH.It is wellknown that the tidal forces cause the body to be radially stretched while compressed in the angular direction for the Schwarzschild BH.For charged BHs,the tidal forces can stretch or compress a body in any direction.[20]For dyonic RN BH,the strength of this tidal force depends upon charge-to-mass ratio that involves both electric and magnetic charges.It turns out that geodesic deviation vector behaves qualitatively identical for charged and uncharged BHs away from the horizon.However,the corresponding vector behaves quite differently for Schwarzschild,RN and dyonic RN BHs inside the event horizon.In particular,the radial geodesic component vanishes for certain initial conditions but its angular components remain finite for charged BHs.For uncharged BHs,the radial geodesic components become in finite,whereas the corresponding angular components become zero near the singularity.[23−24]Thus,a magnetic charge plays a substantial role in stretching and compression of bodies near dyonic RN BH.It is worth mentioning here that the results for RN BH can be recovered withQm=0.[20]

[1]S.Chandrasekhar,The Mathematical Theory of Black Holes,Oxford University Press,Oxford,UK(1983).

[2]V.P.Frolov and Z.Zelnikov,Introduction to Black Hole Physics,Oxford University Press,Oxford,UK(2011).

[3]P.O.Mazur,J.Phys.A 15(1982)3173.

[4]S.Bellucci,Supersymmetric Gravity and Black Holes,Springer(2013).

[5]M.Calvani and Z.Stuchlik,Nuovo Cimento B 70(1982)128.

[6]Z.Stuchlik,Bull.Astron.Inst.Czechosl.34(1983)129.

[7]I.Semiz,Class.Quantum Gravt.7(1990)353.

[8]K.S.Virbhadra and J.C.Parikh,Phys.Lett.B 331(1994)302.

[9]A.Ghosh and P.Mitra,Mod.Phys.Lett.A 11(1996)2933.

[10]M.Sharif and S.Iftikhar,Int.J.Mod.Phys.D 26(2017)1750091.

[11]B.Mashnoon and D.S Theiss,Phys.Rev.Lett.49(1982)1960.

[12]U.Kosti´c,et al.,Astron.Astrophys.496(2009)307.

[13]R.Brito,V.Cardoso,and P.Pani,Phys.Rev.D 86(2012)024032.

[14]D.H.Fuchs,Ann.Phys.495(1983)231.

[15]S.L.Ba˙za´nski and P.Jaranowski,J.Math.Phys.30(1989)1794.

[16]M.Visser,Phys.Rev.D 88(2013)044014.

[17]K.R.Symon,Mechanics,Addison-Wesley(1971).

[18]M.P.Hobson,et al.,General Relativity An Introduction for Physicists,Cambridge University Press,Cambridge(2006).

[19]R.D’Inverno,Introducing Einsteins Relativity,Clarendon Press,Oxford(1992).

[20]L.B.C.Crispino,et al.,Eur.Phys.J.C 76(2016)168.

[21]B.F.Schutz,A First Course in General Relativity,Cambridge University Press,Cambridge(1985).

[22]R.Koley,S.Pal,and S.Kar,Am.J.Phys.71(2003)1037.

[23]R.M.Gad,Astrophys.Space Sci.330(2010)107114.

[24]C.W.Misner,K.S.Thorne,and J.A.Wheeler,Gravitation,Freeman,New York(1973).