Dynamics of the Smooth Positons of the Wadati-Konno-Ichikawa Equation∗

Gai-Hua Wang(王改华),Yong-Shuai Zhang(张永帅),and Jing-Song He(贺劲松)

1Department of Mathematics,Ningbo University,Ningbo 315211,China

2School of Science,Zhejiang University of Science and Technology,Hangzhou 310023,China

1 Introduction

Wadati,Konno,and Ichikawa(WKI)derived two highly nontrivial nonlinear equations in 1979.[1]These equations are the WKI-I equation

Both of them can be related to AKNS system by a series of gauge transformations.[2−3]Recently,by applying hodograph transformation Note that Eq.(4a)holds automatically according to Eqs.(4b),(4c),and(5).

The mWKI equation is a very special equation in integrable systems,because it has bright solitons from vacuum for defocusing system(r=q∗,asterisk denoting complex conjugate)and focusing system(r=−q∗)simultaneously,which is never displayed until the appearance of our recent work.[4]In addition,the soliton solution,breather solution and rogue wave solutions[4]of the mWKI equation are also constructed by the Darboux transformation(DT).Here,we will study the mWKI equation with degenerated DT[5]and give the formula ofN-th order degenerated solution,which yields positon solution and breather-position(b-positon)solution.

Positon solution was first found by Matveev in 1992 for Korteweg de Vries(KdV)equation when the spectral parameters are approaching the same value,[6]then it was quickly extended to the sine-Gordon equation,[7−8]the modi fied KdV equation,[9−10]sinh-Gordon equation,[11]and so on.Similar to the soliton solution,positon solution is a fundamental solution generated from zero background for nonlinear integrable equation,and exhibits many interesting properties. Even though soliton and positon solutions are different,they also have connections,[12]In general,positon solutions are viewed as long-range analogues of solitons and they are slowly decreasing,oscillating solutions.[13]In addition,relationship between positon solution and breather solution is shown in Ref.[12].

The positon solution belongs to the “Hirota family”and can be derived from the standard second order soliton by a proper limiting procedure.[14]The detailed derivation of a second order positon solution of the KdV equation from a second order soliton solution has been given by Kurasov.Different from the soliton solutions,two positons remain unchanged after mutual collision.[15−16]Since the positon solutions are mainly found in the real-valued equations,[17−19]and these solutions are singular.The mWKI as a complex-valued physical model is deserved to be further studied for the following reasons:(i)Are there smooth positon solutions in the complex-valued equation like the mWKI?(ii)How to calculate the trajectories before and after collisions of positon solutions? (iii)The WKI equation admits saturable nonlinearity,and the bpositon solutions are useful for generating the rogue waves in optics,[20]so the study about b-positon solution of the mWKI has potential value in optics.

2 Degenerated Solutions of the mWKI Equation

The Lax pair of the WKI-I equation[1]is given by

Hereψ(X,T,λ)is an eigenfunction associated with eigenvalueλ.

Similar to the determinant representation of then-fold DT for the nonlinear Schrödinger equation,[21−22]thenfold DT of the mWKI equation has also been given in a determinant form.[4]For convenience,we display the formula ofN-th order solution generated by then-fold DT and reduction condition in appendix.

Remark 1This paper only considers the focusing case,but the similar procedure can also be conducted to the defocusing case.

Set “seed” solutionr=q=0,thenζ=1.Furthermore,selectλk=ξk+iηk,the eigenfunction associated with the“seed” solution is given by

then new solutions generated by then-fold DT satisfy the reduction conditionq[n]=−r[n]∗.

According to reduction condition and the formula ofN-th order solution given in Eq.(A1),the first order soliton solution of the mWKI equation is

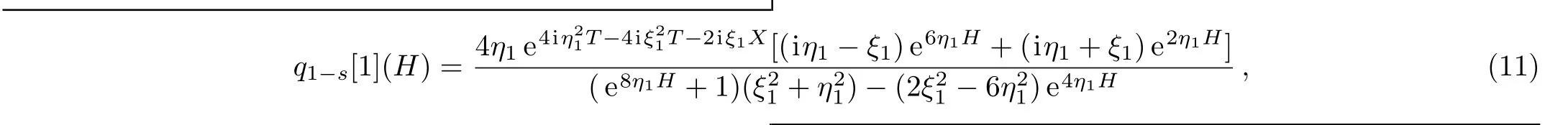
withH=X+4ξ1T.This solution has been given in Ref.[4]and it will be used to study the decomposition of positon solutions.

Similar to Ref.[6],when eigenvalues also go to the same value in formulas,it produces the degenerated solution(or positon),and in this case,the formula given by Eq.(A1)in appendix becomes degenerated.The formulas ofN-th order degenerated solution(or positon)of the mWKI equation are obtained by this limit procedure.

Theorem 1TheN-th order positon solution of the mWKI equation with the focusing condition are

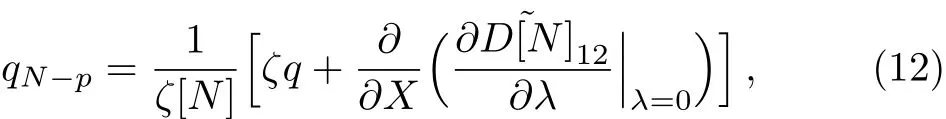
andni=[(i+1)/2],[i]denoting the fl oor function ofi.Remark 2This theorem also holds for the degenerated breather(b-positon)generated from a nonzero “seed” solution by then-fold DT.We shall discuss b-positon later.

SetN=2,using formulas given in Eq.(A1)(see appendix),a second order soliton solution of the mWKI equation is obtained as

Then,from the formula given in Theorem 1,the fundamental positon(the second order positon)solution is given by setting,which is in the form of

The pro file of the fundamental positon solution is displayed in Fig.1.As is well known,trajectories of the second order soliton solutions are two straight lines before and after collision,but there exists a phase shift which is a constant.However,the trajectories of the fundamental positon solutions are two curved lines and the phase shift is an undetermined function ofT.In order to get phase shift,we assume the|q2−p|2can be decomposed as follows:

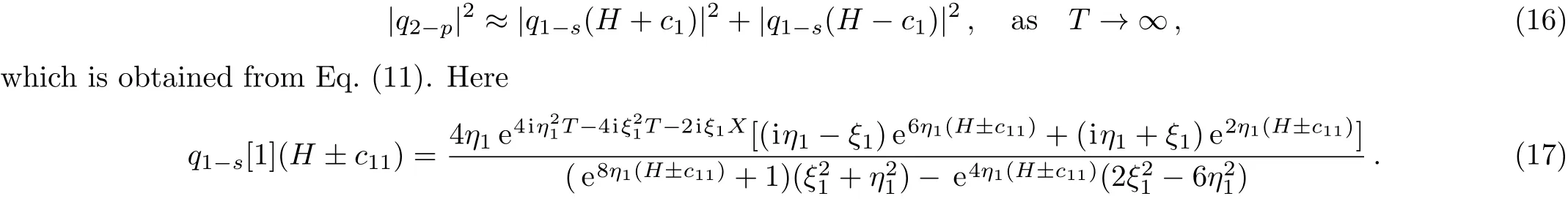
Substituting Eq.(17)into Eq.(16),and just considering the approximation in the neighbourhood ofH=0,it yields

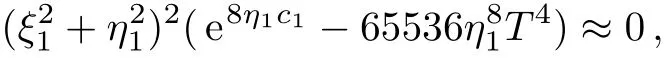
which leads toIt is easy to getc1=ln(T4)/8 whenT→∞.In summary,we get following theorem on the decomposition of the positon.

Corollary 1AsT→∞,the modulus square of the fundamental positon can be decomposed as

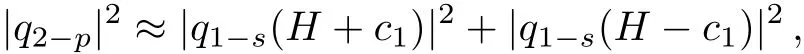
with phase a variable shiftc1=ln(T4)/8.

The result given in Theorem 1 is veri fied by an excellent agreement between the density plot and the approximate orbit of the decomposition in Fig.2.Actually,in Fig.2,we display the trajectories of fundamental positon by its density plot(green line),and the approximate orbits derived by the decomposition in red solid line.The red line overlaps the green line very well whenTis sufficient large.

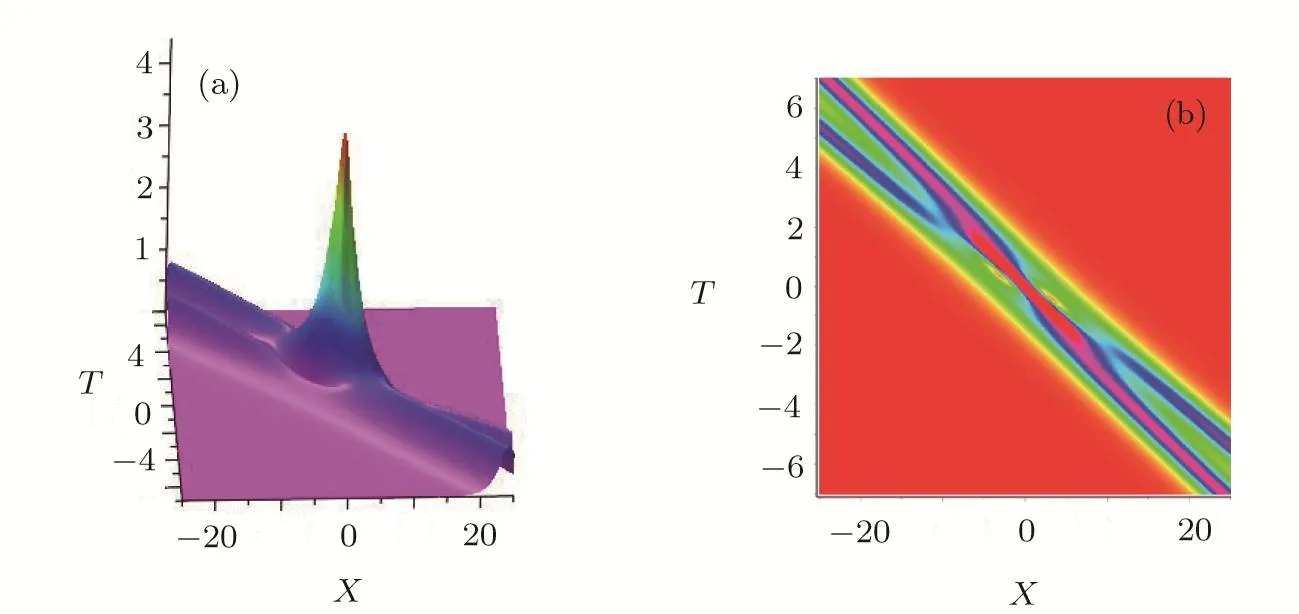
Fig.1 (Color online)The evolution of the fundamental positon solution|q2−p|for the mWKI equation with ξ1=1 and η1=0.35.

Fig.2(Color online)The density plot(green line)of the fundamental positon solution|q2−p|for mWKI equation.(a) ξ1=1 and η1=0.30.(b) ξ1=1 and η1=0.35.The red solid line denotes the approximate orbit of the decomposition.

Moreover,according to the above decomposition method,we can get the similar results for the higher order positon solutions.In order to further show the validity of this method,we provide another example.

Corollary 2AsT→∞,the third order positon solution of the mWKI equation can be decomposed as Substituting nonzero“seed”solution given in Eq.(18)and eigenfunctions given in Eq.(19)back in to Theorem 1,we can obtain theN-th order b-positon solution of the mWKI equation.The fundamental b-positon solution describes the interaction of two breather solutions,which is similar to the fundamental positon solution that displays the interaction of two solitons in degenerated case.The figures of the b-positon solution are shown in Fig.3.Further,the higher-order b-positon solution will reduce to a higher-order rogue wave under the parameter conditionsA=1 andC=1/2 as the appearance of the first order rogue wave.[4]

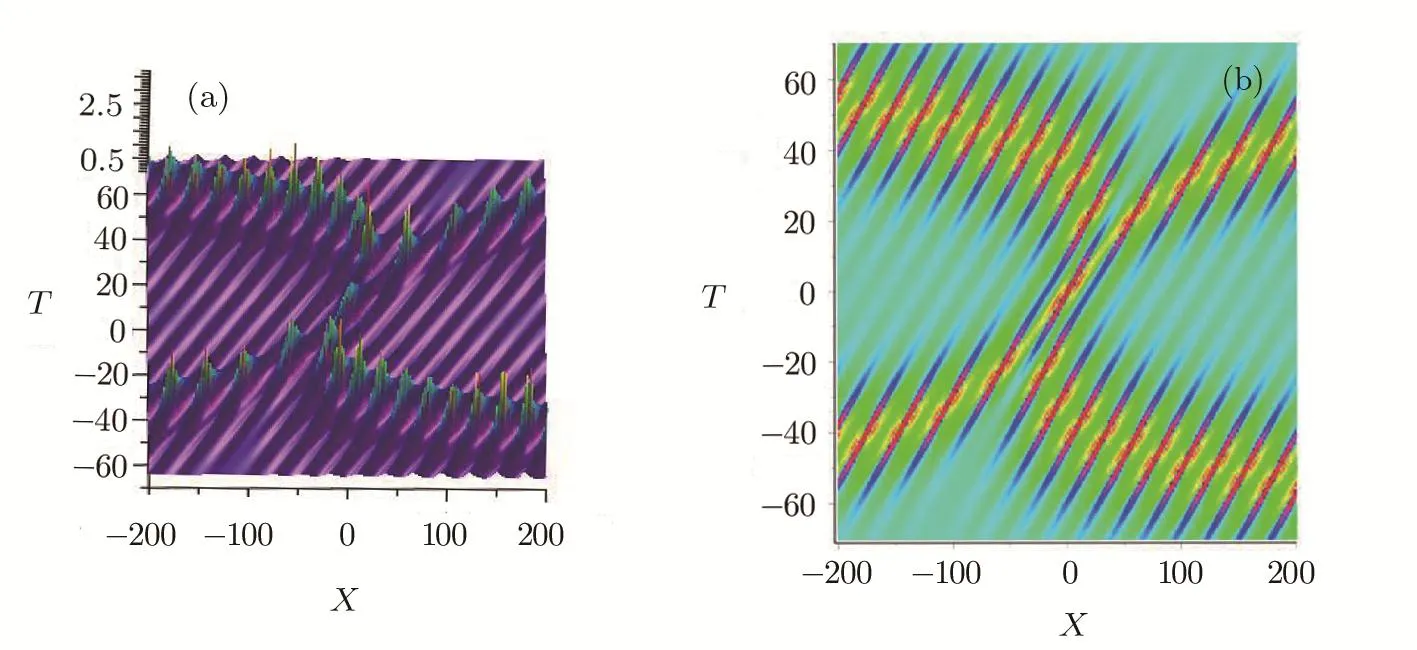
Fig.3 (Color online)The dynamic evolution of a fundamental b-postion solution for the mWKI equation with ξ1=1,η1=0.3.

3 Summary and Discussion

This paper mainly discusses the mWKI equation,which is equivalent to the WKI-I equation by a hodograph transformation.The determinant representation of theN-th order smooth degenerated solution for the mWKI is presented in Theorem 1.According to this representation,formulas of two kinds of degenerated solutions are obtained,i.e.,positon solution and b–positon solution.Additionally,based on the decomposition of modulus square,the approximate orbits of the second order positon solution and the third order position solution are given in Corollary 1 and Corollary 2,which overlap trajectories(i.e.density plots)of the positon solutions very well.Moreover,the phase shift in a positon solution is a function ofT,which is different from the multi-soliton solution.

Appendix

The formulas ofN-th order solution generated by then-fold DT of the mWKI equation are

andD[n]ijdenotes the entry in thei-th row andj-th column ofD[n].

The reduction conditionr=−q∗is preserved if and only if

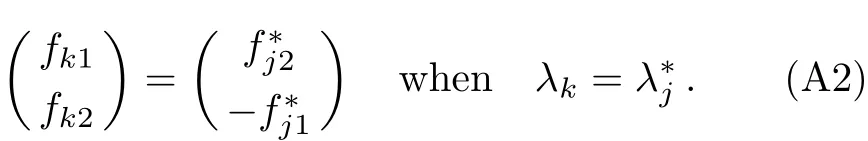
[1]M.Wadati,K.Konno,and Y.H.Ichikawa,J.Phys.Soc.Jpn.47(1979)1698.

[2]M.Wadati and K.Sogo,J.Phys.Soc.Jpn.52(1983)394.

[3]Y.Ishimori,J.Phys.Soc.Jpn.51(1982)3036.

[4]Y.S.Zhang,D.Q.Qiu,Y.Cheng,and J.S.He,Theor.Math.Phys.191(2017)710.

[5]J.S.He,H.R.Zhang,L.H.Wang,et al.,Phys.Rev.E 87(2013)052914.

[6]V.B.Matveev,Phys.Lett.A 166(1992)205.

[7]R.Beutler,J.Math.Phys.34(1993)3098.

[8]V.A.Andreev and Y.V.Brezhnev,Phys.Lett.A 38(1995)58.

[9]A.A.Stahlhofen,Ann.Phys.504(1992)554.

[10]C.Rasinariu,U.Sukhatme,and A.Khare,J.Phys.A:Gen.Phys.29(1996)1803.

[11]R.Beutler,Positon Solutions of the Sinh-Gordon Equation,inNonlinear Coherent Structures in Physics and Biology,edited by K.H.Spatschek and F.G.Mertens,Springer-Verlag,New York(1994)pp.267–270.

[12]R.Beutler,A.Stahlhofen,and V.B.Matveev,Phys.Scr.50(2006)9.

[13]V.B.Matveev,Theor.Math.Phys.131(2002)483.

[14]M.Jaworski and J.Zagrodziski,Chaos,Solitons&Fractals 5(1995)2229.

[15]K.W.Chow,W.C.Lai,C.K.Shek,and K.Tso,Chaos,Solitons&Fractals 9(1998)1901.

[16]P.Dubard,P.Gaillard,C.Klein,and V.B.Matveev,Eur.Phys.J.Spec.Top.185(2010)247.

[17]D.J.Zhang and D.Y.Chen,J.Phys.A:Gen.Phys.37(2004)851.

[18]H.X.Wu,Y.B.Zeng,and T.Y.Fan,Commun.Nonlinear Sci.Numer.Simulat.13(2008)2146.

[19]H.C.Hu and Y.Liu,Phys.Lett.A 372(2008)5795.

[20]L.H.Wang,J.S.He,H.Xu,et al.,Phys.Rev.E 95(2017)042217.

[21]V.B.Matveev and M.A.Salle,Darboux Transformations and Solitons,Springer-Verlag,Berlin(1991).

[22]J.S.He,L.Zhang,Y.Cheng,and Y.S.Li,Sci.China Ser.A 49(2006)1867.