γ－γ符合法测量正电子源活度实验教学研究

覃 雪，张京隆，构文龙，秦 雷，周 荣

(四川大学 物理科学与技术学院，四川 成都 610064)

在核物理基础实验研究中，放射性活度是最直接、最重要的参数。放射性活度的测量与核科学领域各个方面的发展有十分密切的关系。例如放射性核素的生产及其在工、农、医等学科研究中的应用，以及环境监测等方面都涉及放射性活度测量[1－3]。符合法测量因其可以排除探测效率等因素对测量结果的影响，从而被广泛应用于放射源活度的精确测量[4－5]。为了提高本科生的学术视野和加深学生对放射性活度测量的理解，在本科核物理实验中开发符合法测放射源活度这一实验就显得尤为重要。开设该实验可培养学生的动手能力和思考能力，让学生在动手操作实验的过程中真正理解符合法测量放射源活度这一实验技术内涵，这无疑对他们今后从事更为先进的工作具有非常重要的意义。

1 实验设计思想与方案

本实验采用22Na作为被测量的正电子源。22Na的半衰期为2.6 a，在短时间的测量过程中可忽略其活度的变化。22Na从3＋的自旋态到0＋的自旋态衰变过程是比较简单的，只有EC俘获和β＋衰变两种类型，其中β＋衰变的分支比为89.90%。该过程放出的正电子进入物质后很快被慢化，然后在正电子径迹末端遇负电子即发生湮灭，放出2个能量为0.511 MeV的γ光子，2个湮灭光子的发射方向相反，并且湮灭光子的发射是各向同性的。基于这种特性，通过两个能量为0.511 MeV的γ光子符合来测量22Na的绝对活度。

利用符合法测量22Na绝对活度的实验系统框图如图1所示。探测器输出信号依次经过前置放大器和线性放大器放大和成形，单道脉冲幅度分析器幅度分选，延时器延时，延时后的信号分别进入计数器计数，同时两路延时信号进入符合器进行符合计数，最终利用计数器I、II和符合计数器的结果反推22Na的活度。

图1 符合法测量放射源活度实验系统框图

2 探测器实验平台设计

图2 探测器实验平台

传统的实验教学中，图1的Part.A部分中探测器位置都是人为摆放的，这会给实验带来以下3个问题:1)不能保证探测器和放射源中心同轴，这会给最终实验结果带来较大误差；2)探测器移动不方便，并且移动距离需要人为测量，这给实验的进行带来不便；3)搭建探测器费时费力，不利于实验的进行。为了解决以上问题，首次设计了一个针对符合测量的探测器实验平台，如图2所示。探测器平台由放射源固定装置、探测器固定装置、位置调节平台以及铅屏蔽体组成。放射源固定装置，能够方便地将放射源放置到屏蔽体内。两个探测器安装到探测器固定装置上，机械设计上保证了放射源、两个探测器中心同轴。由于实验过程中需水平移动探测器至不同距离测放射源活度，增加了带有标准刻度的位置调节平台。同时，考虑到放射源对实验操作人员的辐射伤害，本实验平台设计了铅屏蔽体，屏蔽之后实验操作人员活动区域的剂量应满足环境限值 (剂量当量率4 μSv/h)[6]。该探测器实验平台的使用，一方面使学生在操作实验时更加准确方便；另一方面也确保了学生操作实验的安全，这些都更符合学生实验的要求。

3 实验内容设置

3.1 活度公式推导

用探测器实验平台和后续电子学仪器搭建好的实验系统进行22Na放射源活度的符合测量。首先对γ－γ符合法测22Na活度公式进行推导[7]。如图3所示，实验中探测器1与放射源之间的距离相对于探测器2要小一些，放射源与两探测器的轴线在同一直线上。

图3 实验中探测器与放射源相对位置示意图

第1道 (探测器1)的计数率为:

第2道 (探测器2)的计数率为:

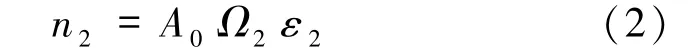
式中，A0为22Na放射源β＋衰变活度；Ω1和Ω2分别为两探测器对源所张的相对立体角；ε1为探测器1对γ的探测效率，ε2为探测器2对γ的探测效率。由于两个湮没光子的发射方向相反，并且Ω1＞Ω2，因此假设一对湮没光子中的一个进入探测器2，则另一个必然进入探测器1。故而符合道的真符合计数率为:

由式(1)～式(3)可得放射源活度的表达式为:

式 (4)中说明放射源的活度只与两个γ道和符合道的计数率以及探测器1对源所张的相对立体角Ω1有关。

实验中还要考虑符合分辨时间内产生的偶然符合计数，对其进行修正可以得到:

式中:τ是符合分辨时间；nc为符合道率计数率，包括真符合计数率和偶然符合计数率。

3.2 测定22Na脉冲幅度谱

22Na衰变到22Ne的激发态，退激到基态过程中会发射出1.275 MeV的γ射线，符合测量选用的是β＋湮灭产生的两条0.511MeV的γ射线，因此在脉冲符合之前需要通过幅度分选对脉冲进行幅度判别。如图1所示搭建的实验系统，测得22Na的脉冲幅度谱。

给探测器加合适的高压，调节放大器成形时间和放大倍数，使各级输出波形稳定不失真。保持单道道宽不变，从零改变下阈，测得每一阈值下的输出脉冲计数，便可得到幅度谱。如表1所示，为对应阈值下探测器1测得的22Na输出脉冲计数。

表1 探测器1在对应阈值下测得的22Na输出脉冲计数

由表1得到22Na脉冲幅度谱如图4所示。

图4 探测器1测得的22Na脉冲幅度谱

由图4所示，可以发现在3 V左右一个峰，此峰即为0.511 MeV能量的γ射线全能峰。在6.6 V附近有一个峰，此峰为1.274 5 MeV能量的γ射线全能峰。因此通过该脉冲幅度谱可以确定单道1的上阈和下阈分别设置为3.5 V和2.5 V。同理可以确定单道2的上阈和下阈分别设置为3.1 V和2.1 V。

3.3 测定符合分辨时间

符合电路能够产生符合输出的两道输入脉冲的最大时间间隔τ称为符合分辨时间。τ的大小与输入脉冲的宽度有关。当两个脉冲的时间间隔小于τ时，一部分脉冲将重叠成大幅度脉冲并触发成形电路输出一个符合脉冲。反之，就没有符合脉冲输出[8]。

符合分辨时间τ决定了符合装置研究各种关联事件的精度。因此，做符合测量实验时，必须先测定符合分辨时间。具体方法有以下两种。

1)偶然符合法测符合分辨时间。若对不可能产生真符合计数的两个源作符合测量时，符合脉冲均为偶然符合，可得到偶然符合计数率与符合分辨时间的关系[9]。假设两符合道的脉冲均为理想的矩形脉冲，其宽度为τ，再设第1道、第2道的平均计数率分别为n1、n2，则偶然符合计数率为:

可见nγc与n1n2呈线性关系，实验中可改变某些实验条件，做多次测量，得到一组nγc与n1n2关系的数据，即可画出nγc－n1n2的关系直线，通过求直线斜率即可得到符合分辨时间τ。

实验用两个137Cs源作偶然符合。用一定厚度的铅砖将两个放射源及探测器隔开，如图5所示。

图5 偶然符合法测符合分辨时间示意图

探测器1只探测到1号137Cs的信号，探测器2只探测到2号137Cs的信号，第1道探测到的放射源产生的脉冲计数率为n1，第2道探测到的放射源产生的脉冲计数率为n2，则n1和n2是毫无关系的脉冲信号计数率，它们的符合计数率nγc是偶然符合产生的。改变放射源位置，得到一组数据如表2所示。

表2 第1道、第2道和符合道计数率

用最小二乘法线性拟合如图6所示。

图6 nγc－n1n2 线性拟合示意图

得到直线斜率为:2τ＝2.173×10－6s。符合分辨时间τ＝1.086×10－6s ＝1.086 μs。

2)瞬时符合法测符合分辨时间。在符合测量装置中，人为地改变两符合道的相对延迟时间td时，符合计数率随延迟时间td的分布曲线称为延迟符合曲线。对于瞬发事件，即发生的时间间隔远小于符合分辨时间τ的事件，所得延迟符合曲线称为瞬时符合曲线[10]。

将22Na放射源放在两个γ探头的中间，用γ－γ信号作瞬时符合测量，调节符合装置插件上的延迟时间td，逐点测量符合道的计数Nc，并得到计数率nc，做出符合计数率随延迟时间的曲线图，如图7所示。

图7 22Na源γ－γ瞬时符合曲线

由图7可知，瞬时符合曲线的半高宽FWHM＝2τ＝2.00 μs，因此τ＝1.00 μs。

以上两种方法测得的符合分辨时间数值上大致相等，但由于实验条件不同，物理意义不同，不能求平均值。计算时只能取与进行符合测量时相同条件下测得的符合分辨时间值。

3.4 测22Na的绝对活度

在与瞬时符合法测符合分辨时间相同的实验条件下，根据图7的瞬时符合曲线，把延迟时间调至1.5 μs，这样能确保装置获得γ－γ符合的最佳真符合状态。选择合适的时间，用三路定标器测量两个γ道的计数率n1、n2和符合道计数率nc。实验用22Na放射源为点源，NaI晶体的尺寸为Φ4.5 cm×4.5 cm，实验中固定探测器1与放射源的距离为0.5 cm，改变探测器2与放射源的距离，测量结果如表3所示。

表3 22Na活度测量结果

表3中，n1、n2和nc分别是γ道1、γ道2和符合道的计数率，为真符合计数率，A0为22Na放射源β＋衰变的活度，A0基本与探测器2和放射源的距离无关。对计算结果取平均值，得到A0＝18 924 Bq。已知β＋衰变的几率为89.90%，可以计算得到22Na放射源活度A＝20 910 Bq。

已知t时间内测得的计数为N，则计数率n的标准差，根据误差传递公式，最后计算的活度A的标准差σA＝82 Bq，故得A＝(20 910±82)Bq。

4 结束语

本文针对传统实验教学的不足，自主设计了一套符合法测量正电子源22Na活度的探测器实验平台，利用该平台和后续电子学仪器测得22Na的绝对活度。该平台一方面增加了符合测量实验的准确性和方便性，另一方面有效地保证了学生的实验操作安全。该平台具有很好地移植性，可以在其他高校以及更多的核物理实验如正电子在物质中湮没寿命测量中进行推广使用。在实验上，共设计了4个实验内容，其中单道脉冲幅度分析器上下阈值的选择是重点，它将直接影响活度测量的准确性，实验通过测量不同阈值下的计数率得到22Na的脉冲幅度谱，根据幅度谱确定单道阈值。这种方法简单直观，锻炼学生的动手能力的同时也能更理解单道和多道的原理。符合分辨时间的测量是本实验的难点，采用两种不同的方法测量符合分辨时间，更有助于加深理解。本次活度的测量结果是在两个探测器距离放射源不相等距离的条件下得到的，学生实验的过程中，可以研究相同距离下活度的公式推导以及测量结果，这可以很好地加深他们对实验内涵的理解。

[1]谢菊英，马慧，胡玉荣，等.137Cs和90Sr－90Y混合源的β放射性强度教学实验研究[J].实验科学与技术，2014，12(4):40－43.

[2]汤敏敏，刘建中，武志芳，等.日尿排泄1311I值估算甲状腺癌患者体内残留活度[J].中国医疗前沿，2013，8(6):8－9.

[3]李奇，王世联，樊元庆，等.133Xe活度浓度的绝对测量[J].原子能科学技术，2011，45(4):385－388.

[4]BUCKMAN S M，IUS D.Digital coincidence counting[J].Nuclear Instruments and Methods in Physics Research A，1996，369(2－3):368－374.

[5]BUTCHER K S A，WATT G C，ALEXIEV D，et al.Digital coincidence counting－initial results[J].Nucl Instrum Methods A，2002，450(1):30－34.

[6]夏益华主编.高能电离辐射防护教程[M].哈尔滨:哈尔滨大学出版社，2010.

[7]王忠海，覃雪，周智，等.基于波形数字化的γ－γ符合测量[J].核电子学与探测技术，2012，32(11):1293－1296.

[8]复旦大学，清华大学，北京大学合编.原子核物理实验方法上册[M].北京:原子能出社，1985.

[9]程敏熙.符合测量实验方法研究[J].大学物理，2002，21(6):28－32.

[10]林木欣.近代物理实验教程[M].北京:科学出版社，1999.