建模分析中的联合正态分布与仿真

李明奇，覃思义

(电子科技大学 数学科学学院，四川 成都 611731)

在多源信号的输入建模中，输入信号一般是随机的，或者受随机扰动的影响。这些高维输入的随机性经常通过正态随机向量进行刻画。在模型随机分析中，正态随机向量常常需要做变换才能得到输出，线性系统就是常见的一类变换。经线性变换得到的随机向量在许多工程问题与系统建模中非常重要[1]。

正态随机向量各分量线性组合的分布问题，已经有许多研究结论，并且许多文献都构造了应用实例。文献[2]构造了两个分量都服从标准正态分布的二维随机向量，其分量之和不服从一维正态分布。文献[3]给出了两类非线性数值函数f(x)，使得复合随机变量f(x)仍然服从标准正态分布。文献[4]给出了若干非线性函数，使得复合随机变量仍然服从正态分布。文献[5]给出了非独立的正态随机变量其线性组合为非正态分布的例子。文献[6]给出了n个正态随机变量其线性组合分布性质的一个充要条件，即在组合系数都非零的情况下该组合变量是非正态随机变量，其任意r(r＜n)个的线性组合均为正态随机变量。文献[7]构造了两个例子，说明了n(n≥2)个正态随机变量之和不是正态随机变量。文献[8]构造了任意n个非独立的正态随机变量之和不是正态随机变量的例子。文献[9]研究了二维正态随机变量的组合问题。

然而，对于联合正态随机向量经变换所得到的新的向量组分布问题所见文献不多，仍然需要深入研究。本文研究服从联合正态分布的向量经过线性变换后是否构成新的联合正态分布的问题，并设计了数值实验进行仿真分析。

由于非标准正态随机变量通过简单的变换就可以变为标准正态分布，本文假设各正态随机变量均值为零，方差为1。此时，相关矩阵与协方差矩阵一致。

首先，讨论线性方程组

的非零解问题。

将线性方程组(1)变换为常见形式:

记αk＝(ck1，ck2，…，ckn)T。 方程组(2)的左端可以写成系数矩阵的列向量线性组合形式:

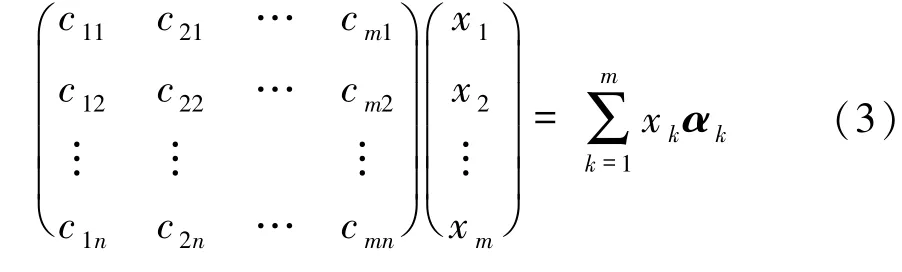
于是，方程组(2)等价于

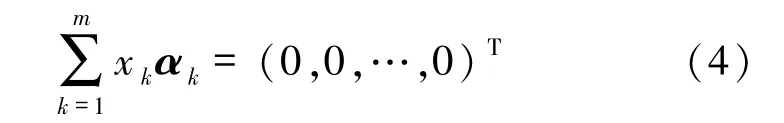
因此，要使线性方程组(1)无非零解，向量组{α1，α2，…，αm}必须线性无关。即矩阵

CT＝列满秩。

从而，在矩阵C行满秩时，方程组(1)无非零解。于是，可以得到引理1:

若线性方程组

(x1，x2，…，xm)C＝(0，0，…，0)，C＝(cij)m×n，cij∈R的系数矩阵满足行满秩，则方程组无非零解；否则方程组有非零解。

1 随机向量线性变换的分布

下面分两种情况讨论正态随机变量组

ζ1，ζ2，…，ζn线性变换的分布。

1.1 n个独立的正态随机变量分布

ζ1，ζ2，…，ζn是n个独立的正态随机变量，ζk～N(0，σ2k)。其相关矩阵B为:

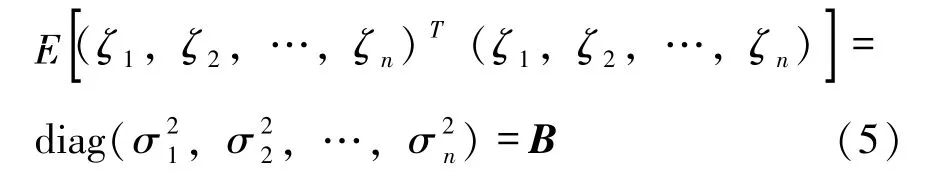
易知，相关矩阵B是正定矩阵。若正态随机变量组ζ1，ζ2，…，ζn的线性变换为:

则随机变量组η1，η2，…，ηn的相关矩阵满足

于是，当‖x‖2≠0时，得到以下两个结论:

1) 若 (x1，x2，…，xm)C＝(0，0，…，0) 无非零解，则对于任意非零向量(x1，x2，…xm)，有

(x1，x2，…，xm)CBCT(x1，x2，…，xm)T＝

[(x1，x2，…，xm)C]B[(x1，x2，…，xm)C]T＞0，

即相关矩阵CBCT是正定矩阵。这时，随机变量组η1，η2，…，ηn服从联合正态分布。

2) 若 (x1，x2，…，xm)C＝(0，0，…，0) 有非零解，则对于任意非零向量(x1，x2，…，xm)，有

(x1，x2，…xm)CBCT(x1，x2，…，xm)T

即矩阵CBCT是半正定矩阵。说明随机变量组η1，η2，…，ηn在这种情况下服从退化的联合正态分布。

以上分析可以归纳为定理1:

ζ1，ζ2，…，ζn，ζk～N(0，σ2k)，相互独立。当Cm×n满足行满秩时，向量 (η1，η2，…，ηn) 服从非退化联合正态分布；否则服从退化的联合正态分布。

1.2 n维非退化的联合正态分布

(ζ1，ζ2，…，ζn)服从n维非退化的联合正态分布，ζk～N(0，σ2k)。其正定相关矩阵B为:

这时，矩阵不一定是对角矩阵。随机向量组(ζ1，ζ2，…，ζn)经过线性变换后得到的向量组(η1，η2，…，ηm) 为:

则相关矩阵B满足

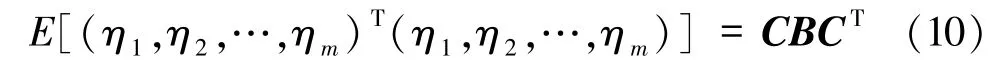
于是，对于任意非零向量x，有

因此，设(ζ1，ζ2，…，ζn)服从n维非退化的联合正态分布，ζk～N(0，σ2k)。其线性变换为:

通过类似于定理1的分析由引理1可以得到如下定理2:

(ζ1，ζ2，…，ζn) 服从n维非退化的联合正态分布，ζk～N(0，σ2k)。当矩阵Cm×n满足行满秩时随机向量(η1，η2，…，ηn)服从非退化的联合正态分布，否则服从退化的联合正态分布。

事实上，定理2是定理1的推广形式。n维联合正态分布问题在建模分析和信号处理中得到广泛的应用。在处理这些问题过程中，定理1和定理2给出了简洁的判定准则，将会使分析过程更加严谨。对于n维联合正态随机向量的非线性变换，其分布情况已有一些成果但仍然需要进一步研究。

2 实例仿真实验

下面，通过对服从二维联合正态分布的数据点的线性变换所得的二维数据进行仿真对比分析。仿真实验过程分以下3个步骤。

1)产生70个二维联合正态分布的数据点(x，y)，其协方差

这些二维正态分布点如图1所示，是以下随机点产生的基础。

图1 正态分布的数据点(x，y)

2)对已经有的二维联合正态分布的数据点(x，y)进行行秩为1的线性变换，由

得到数据点(u，v)，如图2所示。点沿着一根直线随机分布。随机性从二维退化到一维，实验结果与定理2的结论一致。

图2 进行行秩为1的线性变换后的数据点(u，v)

3)对数据点(x，y)进行行满秩的线性变换，由

得到数据点(m，n)，如图3所示。

对数据点(x，y)进行行满秩的线性变换，由得到数据点(α，β)，如图4所示。

图3和图4表明，行满秩线性变换后的点仍然保持了二维随机特征，与定理2的结论一致。

图3 进行行满秩线性变换后的数据点(m，n)

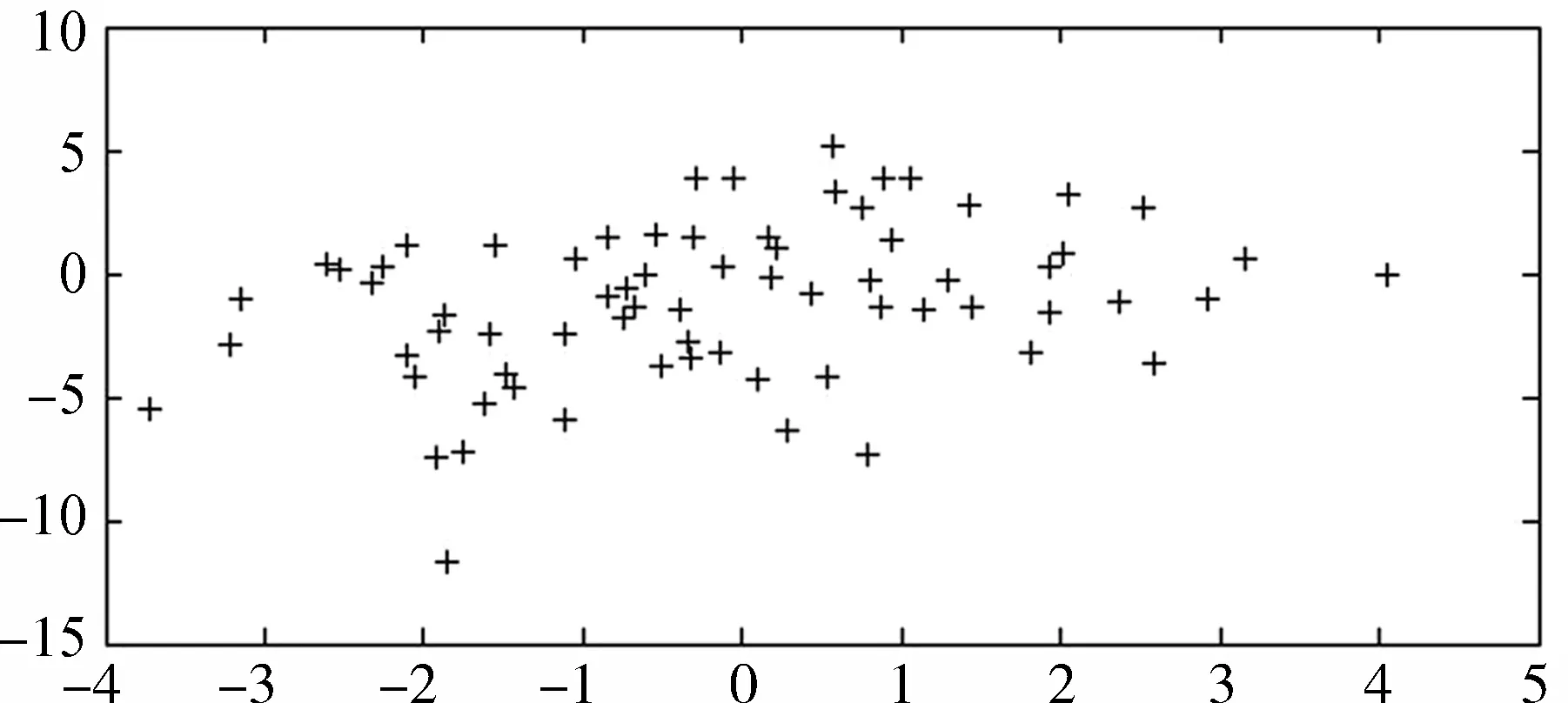
图4 进行行满秩线性变换后的数据点(α，β)

若仿真实验中所产生的二维随机信号是MIMO通信系统中的两根发射天线的发送信号，发射前的线性预处理通常有助于改善信号的特征。若处理不当，将会造成信息的严重损失 (如图2所示)。同时，定理2和仿真结果也说明二维联合正态分布的信号经过行满秩线性映射到两根天线后，发射信号的随机特征不会发生变化；经过非行满秩线性映射到两根或更多天线上，发射信号的随机特征将会发生变化，如图3和图4所示。

3 结束语

对n维联合正态随机向量进行线性变换，根据定理2，只有该变换为行满秩时才能得到服从联合正态分布的新的向量，否则，新向量将服从退化的联合正态分布。仿真实验显示了不同变换情况下点的随机性差异。本文所得判定准则简洁易于分析，其结果有助于高维信号的分析和建模。

[1]ROMANO J P，SIEGEL A F.Counter Examples in Probability and Statistics[M].California:Wadsworth ＆Brooks，1986.

[2]徐全智.关于正态随机变量的线性函数的分布[J].大学数学，1990(z1):153－154.

[3]唐加山.正态随机变量的非线性函数具有正态性的两个例子[J].大学数学，2003，19(1):83－85.

[4]唐加山，赵林.关于正态随机变量函数的正态性[J].南京邮电大学学报(自然科学版)，2001，21(4):60－63.

[5]李亚兰.关于正态随机变量的线性组合分布[J].仲恺农业工程学院学报，2004，17(2):51－55.

[6]尹传存.关于正态随机变量线性组合的分布的一个充要条件[J].数学的实践与认识，1991(2):28－32.

[7]吕黎明.正态随机变量线性组合的分布探讨[J].绍兴文理学院学报，2005，25(9):30－32.

[8]傅自晦.关于正态随机变量线性组合的分布[J].数学的实践与认识，1988(4):38－41.

[9]任耀峰，王玉琢.正态随机变量线性组合的分布问题[J].高等数学研究，2013，16(4):104－106.