高等院校信号与系统课程教学辅助探究与实践

谭北海，彭秋明，姚小娇，胡 超

(广东工业大学 自动化学院，广东 广州 510006)

信号与系统是高等院校通信、电子、计算机、自动化等专业的核心课程，其中的很多概念和分析方法广泛应用于通信、自动控制、信号与信息处理、电路与系统等领域，它以高等数学、复变函数与积分变换及电路原理等课程为基础，是后续相关专业如数字信号处理、通信原理等的先修课程，其教学质量的好坏直接影响到学生对信号、系统和频谱等重要概念的理解及后续课程的学习。由于该课程物理概念抽象、理论性和数学性强，学生对其中的分析方法与基本理论不能很好地理解与掌握[1]。因此，如何让学生更好地理解和掌握课程中的物理概念、基本原理、基本分析方法并灵活运用理论工具解决实际问题是该课程要解决的关键问题。

近年来，国内外高校都引入了MATLAB对该课程中的一些重点难点进行仿真实验，并取得了较好的效果。但现有仿真主要是针对一些独立的知识点进行演示，对于理论课程的繁琐公式、抽象内容帮助不大，因此，传统教学方式缺少一个相对完整的可视化教学辅助演示系统[2]。

信号与系统课程涉及很多数学变换、抽象的概念、定理，对于教师来说，分析起来不便利；对于学生来说，理解起来很困难。而MATLAB的GUIDE(graphical user interface development environment)可以实现图形用户界面，通过图形的方式把这些抽象理论展示出来，使各种变换之间的关系更加直观。因此，本文基于MATLAB的GUIDE工具设计和实现了一个信号与系统可视化演示系统。该系统包含了信号与系统课程的主要教学内容，以简单的参数为入口，通过图形的方式显示计算或仿真结果，有助于提高教学效率，帮助学生更好地理解课程中的重点难点，为信号与系统课程可视化教学和实践提供了积极的帮助[3]。

1 演示系统的框架及特点

1.1 系统框架

MATLAB是MATrix LABoratory的缩写，是一种高级计算机语言和交互式环境。除了用于算法开发、数据可视化、数据分析以及数值计算，MATLAB还可以创建用户界面、连接调用其他编程语言 (如C和C＋＋)。与其他编程软件相比，MATLAB的性能优势主要体现在以下5个方面。

1)编程环境。MATLAB的编程环境是一个集成的开发环境，包括各种命令窗口和工作空间，人机交互性更强，操作更简单。

2)简单易用。MATLAB是一种高级的矩阵/阵列语言，与C＋＋语言相似，但更加简单，更符合科技人员对数学表达式的书写格式，更利于非计算机专业的科技人员使用。

3)强处理能力。MATLAB包含大量数学函数库，可以实现各种数学计算，功能健全丰富。

4)图形处理。具有方便的数据可视化功能，它有一系列绘图函数，可以将向量和矩阵用图形表示，包括二维和三维可视化、图像处理动画和表达式作图；绘图参数包括不同颜色的点、线和多重线，效果非常好[4]。

5)扩展性强。用户可以在MATLAB扩展需要的库函数，也可以调用其他编程语言进行混合式编程；新版本的MATLAB还可以利用MATLAB编译器、C/C＋＋数学库和图形库将MATLAB程序自动转换为独立于MATLAB运行的C和C＋＋代码。

图形用户界面 (GUI)是指由窗口、菜单、图标、光标、按键、对话框和文本框等各种图形对象组成的用户界面，它允许用户定制与MATLAB的交互方式。GUIDE是MATLAB提供的用于GUI界面设计的工具，具有 “所见即所得”的特性，操作简单，用户可以根据需要在GUI组件布局编辑器中添加控件对象，设置控件属性[5－6]，保存文件后会生成相应的.fig图形文件和.m脚本文件。

结合 《信号与系统》教材内容，本文设计的演示系统的结构包括以下6大模块:

1)信号的基本运算 (相加、相乘、平移、尺度变换等)；

2)连续系统时域分析 (连续信号的阶跃响应、冲激响应、零输入响应、零状态响应、卷积运算)；

3)离散系统时域分析 (离散信号的阶跃响应、冲激响应、零输入响应、零状态响应、卷积运算)；

4)傅里叶变换 (幅频特性、相频特性、功率谱等)；

5)拉普拉斯变换 (零极点响应、留数法拉氏逆变换)；

6)Z变换 (零极点响应、幅频特性、相频特性、滤波器特性)。

系统结构框图如图1所示。

图1 演示系统框架图

1.2 系统特点

基于上述系统框架，利用MATLAB的GUI功能，设计搭建的课程演示系统具有以下5个特点。

1)功能齐全，内容丰富。该系统几乎涵盖了信号与系统课程的所有内容。

2)可视化、直观性、交互式。简单的交互式人机互动界面，能直观形象地图形化显示信号与系统课程的抽象内容。

3)自适应不同分辨率的屏幕。该系统采用了屏幕适应性算法，对不同的显示器，程序运行后界面中控件的大小与界面的比例保持恒定。

4)可选择性强。可选择性表现在输入与显示两方面。首先，平台内集成了一些常用的基本输入函数，如符合函数、单位阶跃函数等，因此，输入可以选择调用集成的基本函数，亦可以选择自己填写输入函数。其次，在图形显示上，用户可以根据喜好选择显示图形的线型，如实线型、虚线型、圆圈型等；同时，线条颜色也提供了常见的可选类型。

5)能进行图像处理。在 “傅里叶变换”子模块里，运用傅里叶变换能进行简单的图像处理，除了对图像的一些简单渲染，如 “灰白处理”“浮雕效果”和 “高斯噪声”外，还可以求图像的频谱图、相位特性、平移特性等。

2 演示系统GUI的界面设计

该课程演示系统的GUI界面由主界面和子界面组成，根据系统结构，子界面有6个，各个子界面的功能相互独立。主界面是演示平台的初始界面，它包括进入6个子模块界面的按钮和1个退出演示平台的按钮。主界面主要用于信号与系统各个子模块界面间的来回切换，用户点击其中任意一个子模块按钮便可进入对应的子界面进行演示，如图2所示。

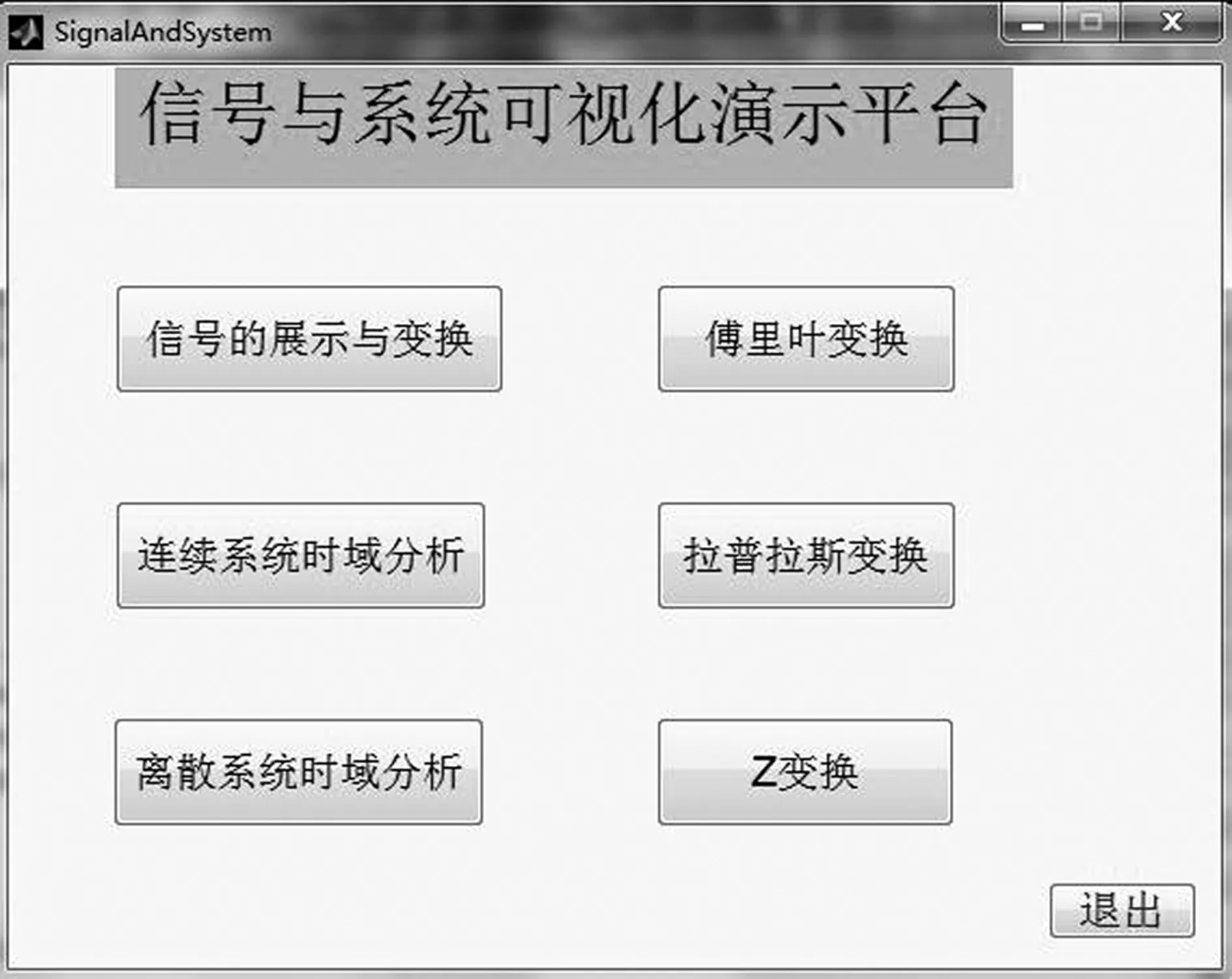
图2 演示平台主界面

当用户点击子模块按钮时，如点击 “信号的展示与变换”子模块，主界面将切换到 “基本信号的展示与变换”界面，如图3所示。进入子界面演示完后，可以点击 “Back”按钮返回主界面，在主界面可以通过 “退出”按钮退出演示平台。

图3 “基本信号的展示与变换”子界面

3 系统演示实例

3.1 LTI系统零输入响应、零状态响应和完全响应

零输入响应是指系统的激励为零，仅由初始状态引起的响应。零状态响应是指系统的初始状态为零，仅由激励引起的响应。完全响应是指由初始状态和激励共同引起的响应。

在演示平台里，为了输入方便，用户输入框中使用Dy，D2y，D3y…表示y的一阶、二阶、三阶导数等；初始条件y(0－)，y′(0－)，y″(0－)… 则写作y(0)，Dy(0)，D2y(0)… 形式。

假设要求解的系统微分方程式:

其激励信号为:

初始条件为:

1)首先求解系统的零输入响应[7]，在主界面点击 “连续系统时域分析”按钮，进入子界面后，将相应的微分方程和初始条件输入，如图4所示；点击 “求解零输入响应”按钮，“化简零输入响应”方框内显示零输入响应结果，如图5所示。

图4 微分方程、初始条件输入

图5 零输入响应

图6 微分方程、激励形式输入

2)接着求解系统的零状态响应，如图6所示，在子界面内输入微分方程和激励形式；点击“求解零状态响应”按钮，“化简零状态响应”方框内显示零状态响应结果，如图7所示。

图7 零状态响应

3)最后求解系统的完全响应，完全响应有稳态响应加暂态响应和零输入响应加零状态响应两种分解方式。如图8所示，将系统微分方程、激励形式和初始状态都输入子界面内。点击 “求解完全响应”按钮，在子界面除了完全响应的解外，还可以看到零状态响应、零输入响应也被求解出来，而且完全响应是这两者之和，如图9所示。

图8 微分方程、激励形式及初始条件输入

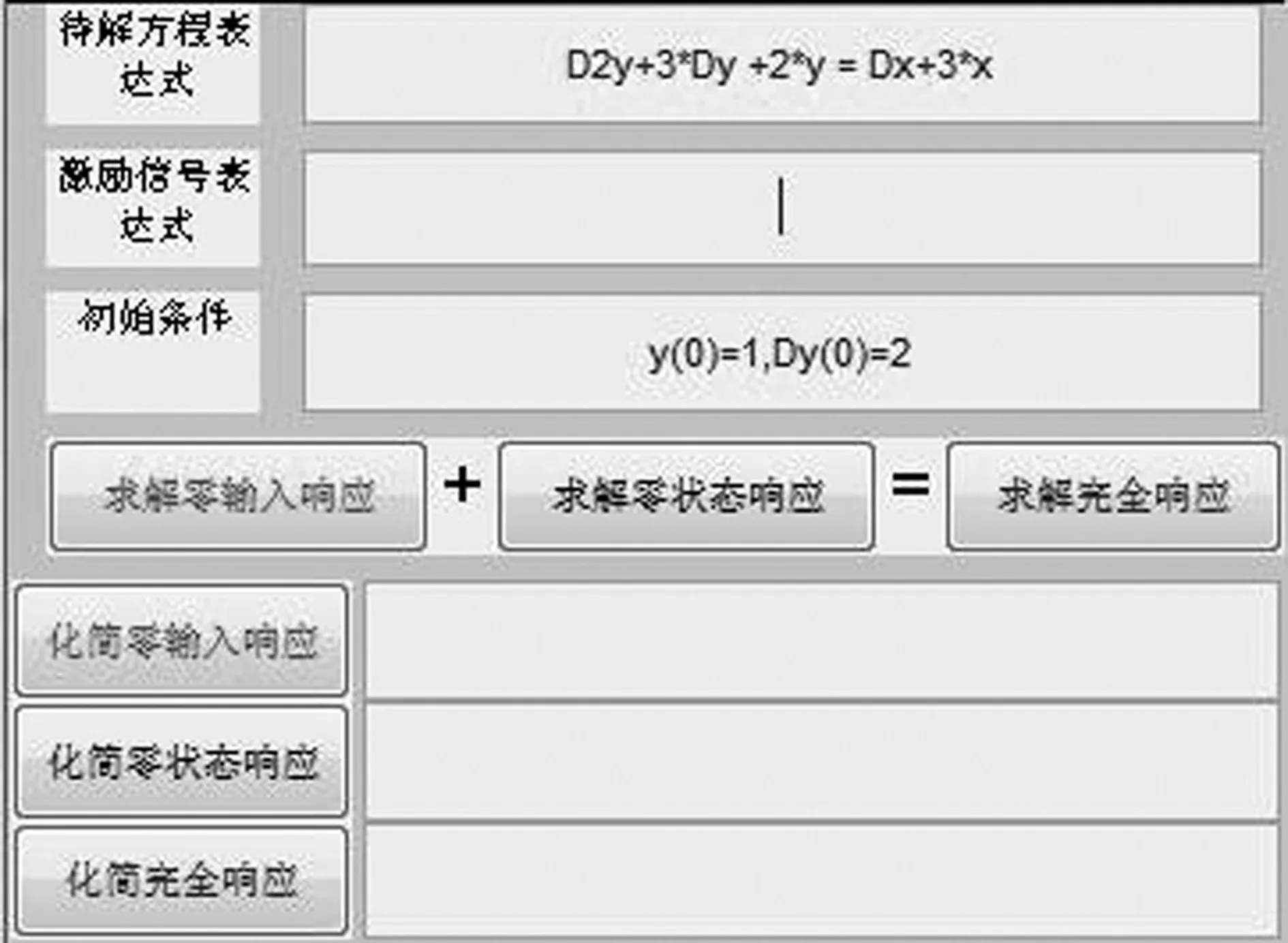
图9 完全响应

通过以上演示，学生能更加直观地理解零输入响应是没有激励信号输入的情形，零状态响应是没有初始状态的情形。对于完全响应，其中一种解法是将其分解成零输入响应和零状态响应。在此基础上，向学生展示数学求解零输入响应、零状态响应、完全响应的过程，加深理论知识的理解，将会达到更好的效果。

3.2 用傅里叶变换进行简单图像处理

首先，观察图像的渲染[8]操作效果，文中渲染效果以彩色图片灰白化处理为例进行演示。从主界面点击 “傅里叶变换”进入子界面后，在路径中选择一个图片添加到程序界面里；然后点击“灰白处理”按钮对选择的图片灰白化，结果如图10所示。

一个图像的高频部分越多，则其轮廓越清晰；一个图像的低频部分越多，则图像越平滑。对图像处理人员来说，图像的频率分布是重要的，观察一个图像的傅里叶变换可以帮助他们把握图像的基本性质[9]。

图10 彩色图片灰白处理效果对比图

图11 图片的傅里叶变换及反变换、傅里叶变换频移及反变换

接下来，观察图片经傅里叶变换后的频谱图及反变换结果，对傅里叶变换后的结果进行频率搬移并对搬移后的频谱图进行反变换，如图11所示。

在这个演示过程中，学生可以发现傅里叶变换还可以应用于图像处理，对应着图像的频谱[10]更直观地知道低频、高频部分对图像的影响，这为传统教学提供极大的便利。

4 结束语

传统的信号与系统课程教学方式多涉及大量的公式推导和理论的讲解，知识点分散且内容抽象，学生不易理解、学习兴趣不高。相比于传统的教学方式，本文设计的基于MATLAB的信号与系统可视化课程演示系统，采用了嵌套式设计，并选取了代表性的典型例子进行详细实例演示，说明了该系统将课程知识和实践系统紧密地结合在一起，搭建了一座从枯燥抽象的理论知识到简单方便的实践演示之间的桥梁。同时，该系统具有良好的界面，简单明了的操作方式以及直观的演示结果，将有助于教师的教学和学生对课程的理解[11]，提高学生的学习效率，调动学生学习的积极性，加强了对课程的掌握能力。

[1]燕慧英，宁宁.“信号与系统”可视化辅助教学系统的设计[J].大众科技，2015，17(2):105－107.

[2]杜世民，杨润萍.基于Matlab GUI的 “信号与系统”教学仿真平台开发[J].试验技术与管理，2012，29(3):1－2.

[3]陈后金，胡健，薛健.信号与系统[M].2版.北京:清华大学出版社，北京交通大学出版社，2005.

[4]彭煜祺.计算软件MATLAB及其应用浅析[J].电脑知识与技术，2015，14(22):204－206.

[5]李秀梅，董文，贾中云.基于Matlab的信号与系统课程GUI演示系统[J].大学教育，2014，3(9):78－79.

[6]翟月英，曾蓉浅析Matlab软件在信号与系统辅助教学中的应用[J].信息通信，2014，28(1):285.

[7]原立格，郝洋洲，崔羊威.基于MATLAB的连续时间LTI系统的时域分析与仿真设计[J].河南科技，2015，40(6):43－45.

[8]邱广萍.MATLAB GUIDE在数字图像处理教学中的应用[J].价值工程，2014，33(3):184－186.

[9]张勇.傅里叶变换在数字图像处理中的应用[J].廊坊师范学院学报 (自然科学版)，2015，15(3):25－27.

[10]朱亚培，龙祖强，刘灿.傅里叶变换在数字图像处理中的教学方法探讨[J].轻工科技，2016，33(2):165－166.

[11]赵玲峰，刘红艳.应用型高校 “信号与系统”课程教学改革探索[J].中国电力教育，2014，30(5):111－112，114.