基于ANSYS/LS-DYNA液压凿岩工作参数的最优值及关联性研究*
罗春雷 ,郑惠斌 ,闵金才 ,程后旗 ,李德明 ,梁健明
(1.中南大学 高性能复杂制造国家重点实验室,湖南长沙410083;2.洛阳耿力工程机械有限公司,河南 洛阳 471132)
在凿岩施工中,提高凿岩速度一直是工程师、学者研究的重点。凿岩速度取决于多方面因素,包括岩石的性质、钎具选用、冲击力、冲击频率、轴推力、转钎速度等。其中,可在凿岩过程中动态调整的工作参数有冲击力、轴推力及转钎速度,本文只对单次冲击过程进行分析,在此不考虑冲击频率的影响,可表示为

式中V——凿岩速度
Fp——冲击力
FT——轴推力
n——转钎速度
以往的研究中,徐小荷等人根据波动理论对凿岩力学进行分析[1],中南大学刘德顺、李夕兵等人从岩石的破碎机理角度得出冲击力学的计算方法[2~8],中南大学杨襄壁老师提出了最优轴推力算法[9],北京科技大学高澜庆采用实验方法对液压凿岩机的主要工作参数进行最优值研究分析[10]。
但这些研究中,缺乏对凿岩工作参数的最优值进行完整的理论论述,并且大多仅对冲击能进行仿真研究[11~14],没有考虑冲击频率与转钎速度。对影响凿岩速度的主要因素及次要因素的研究较少涉及[15]。
为提高凿岩速度,需充分认识影响凿岩速度的敏感因素,并使主要工作参数达到最佳匹配。本文根据岩石破碎力学及波动力学构建数学模型,作为最优值分析的理论依据。采用ANSYS/LS-DYNA对多组工作参数进行仿真,分析上述工作参数是否存在最优值,根据灰色关联度算法得出关联度值,分析影响凿岩速度的主次因素。最后进行实验研究,验证理论分析与仿真结果的准确性。该研究很好地弥补了以往的不足,具有较大的参考意义。
1 凿岩工作参数最优值理论分析
1.1 冲击力及冲击能的最优值分析
根据岩石破碎力学,在钎杆x=l处的凿岩力 Fp可由下式估算[1~8]:
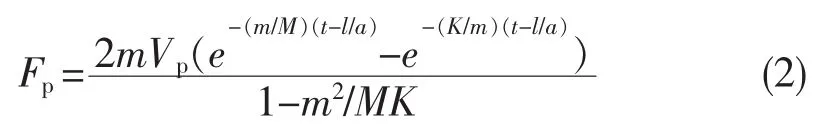
式中m、M——分别为钎杆与活塞的质量
Vp——活塞冲击末速度
t——作用时间
凿岩力与单次凿岩贯入度U及凿岩速度V的关系可表示为:

式中V——钎头移动速度,即凿岩速度
设在一个冲击周期内的平均凿岩力为F¯,则单次凿岩冲击能E可表示为

由上式 (1)(2)(3)可得出钎头处冲击力表达式,因冲击力Fp与凿岩速度成正比关系,单次冲击能E与冲击力Fp的平方成正比关系。冲力Fp越大,则单次冲击能E越大,则单次凿岩贯入度越大,因此冲击力或冲击能无最优值。

图1 冲击过程力学分析
1.2 转钎速度的最优值分析
钎具所受回转扭矩值可以下式推算:

式中M ——总扭矩值
M1——钎杆与岩壁间的摩擦力矩
M2——钎头顶端与接触面产生的摩擦力矩
M3——剪切岩石所需剪力矩
假设岩渣冲洗良好,不考虑摩擦扭矩的影响,则M=M3,由下式估算M3

式中K1——岩石凿痕对岩石强度的影响系数
N——钎头中球齿的个数
Sa——单个球齿的平均剪切岩石面积
τ——岩石的抗剪切强度
图2所示阴影面积可近似为单个球齿的平均剪切面积,可得
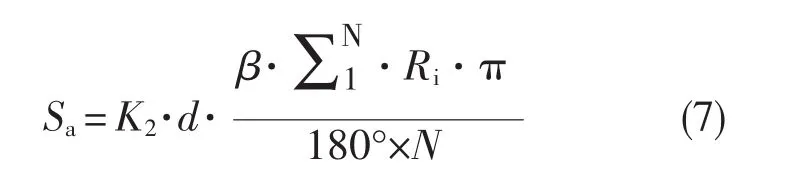
式中K2——剪切系数
d——剪切宽度,近似为球齿的直径
L——剪切长度
β——单周期钎杆的转角
Ri——第i齿中心到中心的距离

图2 单齿平均剪切面积
图3 中,当转钎角偏小(如图3左),则剪切面积较小,凿岩速度慢;当转钎角度偏大(如图3右),剪切面积大。若扭矩超出极限值可能导致卡钎,因此转钎速度也存在最优值。
设防卡钎所允许的转钎扭矩为Mm,单次冲击功最大的转钎角度应为
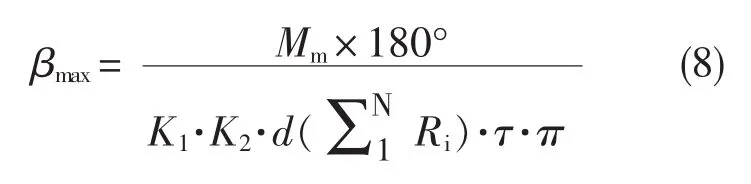

图3 不同转钎角度的剪切面积
则最优转钎速度为

式中f——冲击频率
1.3 轴推力最优值分析
中南大学杨襄壁教授研究了轴推力FT的力学模型,额定轴推力FT可表示为[9]

式中Ff——冲击过程中所受总摩擦力
FG——重力的分力
可知轴推力FT存在最优值,若轴推力太小,凿岩机体因冲击反力回退,钎头无法与孔底保持良好接触。若轴推力太大,则转钎扭转太大,导致钎杆无法正常转动甚至卡钎。
但该公式没有考虑岩石性质的影响。凿岩机与不同岩石之间结合存在最优值。当达到最优值时,凿岩比功耗最小。可由下式估算最优轴推力
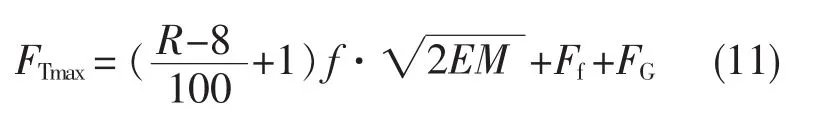
式中R——岩石的普式硬度系数
2 凿岩工作参数最优值仿真分析
ANSYS/LS-DYNA作为著名显示动力学分析软件,适用于冲击碰撞、流固耦合、传热等课题,在国防、航空、汽车、制造等领域有广泛运用。近年来国内在冲压成形、凿岩爆破、贯穿侵彻、汽车碰撞方面做了不少研究,取得了丰硕的成果[11~14]。
2.1 前处理基本参数设定
本文采用Solidworks建立三维模型,将其导入Ansys进行前处理。岩石与钎头的单元属性均设为SOLID164,钎头采用自由网格划分,岩石采用映射网格划分,并对岩石局部细化。三维模型及网格划分结果见图4。

图4 仿真模型及网格划分
因不研究钎具在凿岩过程中的变形,钎头及钎杆材料均选用硬质合金刚YG8,并将其视为刚体,关键字为*MAT_RIGID。岩石选择花岗岩,关键字为*MAT_ISOTROPIC_ELASTIC_FAILURE。具体材料参数见表1、表2。

表1 钎具材料参数值

表2 岩石材料参数值
岩石除接触面以外其余5个面全设置为无边界反射约束(*BOUNDARY_NON_REFLECTING),岩石与钎杆的接触类型设置为面面侵蚀接触(ESTS)。钎杆上需施加冲击力(本文中的冲击力值均指峰值大小)、推进力、转钎速度。仿真时间为 500 μs,冲击力加载时间为 100 μs,作用曲线为三角形脉冲;推进力、转钎速度加载时间为500μs,作用曲线为矩形波;转钎扭矩设为200 N·m。
以往仿真分析大多采用钎头移动量来反应凿岩效果,难以体现转钎速度的作用。凿岩体积改变量与入岩位移成正比,并且其能够很好地体现各个因素的影响,本文研究均通过测量体积的改变量来间接反应凿岩速度。
2.2 仿真结果分析
(1)冲击力对凿岩钻速的影响
将推进力设为18kN,转钎速度设为30rad/s,分别调整冲击力峰值为40、50、60kN,可得如图5a仿真曲线。
由图5a可知:在0~0.025 ms,钎齿刚接触岩石,未能达到破岩临界条件,凿岩体积几乎为零,随后钎杆加速下移,破岩体积迅速增加。因A、B、C的冲击力值不同,因此曲线变化速度也不同。当破岩体积达到最大值之后,各曲线均有不同程度的回升,这是由于只发生弹性应变的单元迅速恢复。对比A、B、C曲线,大致变化趋势相同。然而随着冲击力的增大,破岩体积明显增加,因此冲击力无最优值。
(2)转钎速度对凿岩钻速的影响
图5b将冲击力峰值设定为40kN,推进力设为18 kN,分别调整转钎速度为10、30、50 rad/s。分析图5b可知:在0.2 ms以前,A、B、C破岩体积大致相同,因此段期间岩石破碎主要是与冲击力、推进力有关。在0.2 ms以后,A、B、C三者破岩体积开始出现较为明显的不同。A的转钎速度太慢,相同时间内剪碎的体积较小,因此破岩体积较小。C的转钎速度过快,使得剪切的扭矩过大,影响其正常回转。综上所述,转钎速度也存在最优值。
(3)轴推力对凿岩钻速的影响
图5c将冲击力峰值设为40 kN,转钎速度为30rad/s,分别调整推进力为 8、18、28kN。
分析图 5c可知:在 0.1ms以前,A、B、C 的破岩体积大致相同,因为冲击力值均相同。在0.1 ms以后,B与C的破岩体积明显大于A,这是由于A的推进力较小,使钎头回弹无法与岩石较好地接触。在0.17 ms以后,B的破岩体积大于C,并且一直保持到最终,这是由于C的推进力太大,使得转钎的扭矩增大,影响转动,可知转钎扭矩存在最优值。
上述的仿真结果与第一节的理论分析结论一致,验证了数学及仿真模型的准确性。

图5 不同工作参数的仿真结果
3 凿岩工作参数关联性仿真分析
本节讨论影响凿岩速度的主要因素与次要因素。该研究有利于在凿岩施工找出影响钻进速度的主要问题,对自寻优凿岩控制系统,可根据关联度值设定合理的寻优步长。灰色关联性分析可以很好地衡量特征变量因素与相关因素变量之间的主次关系[15,16],具有计算简便、适用性强的优点。
3.1 灰色绝对相关性计算方法
特征变量数据序列与相关因素变量序列可分别由下式表示

式中n——实验的次数
V——破岩体积
Xi——凿岩相关参数
i——变量的个数
本文研究冲击力、轴推力与转钎速度。因为各个变量之间单位不统一,需先将各个参数值转化成无量纲,算法如下:
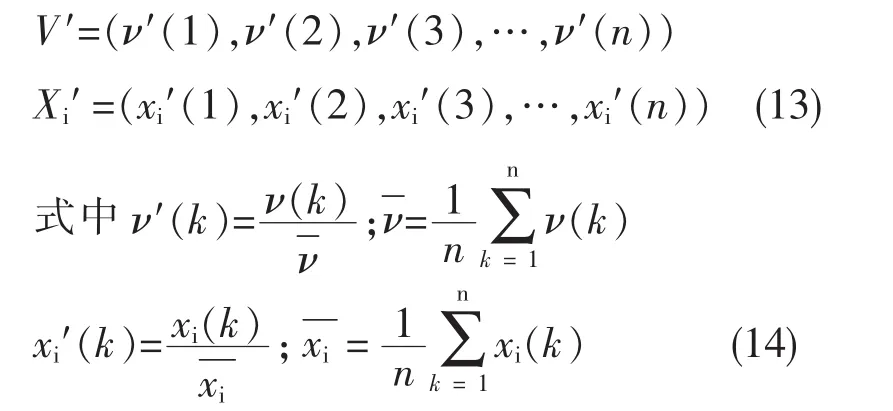
将特征变量与相关因素初始化:
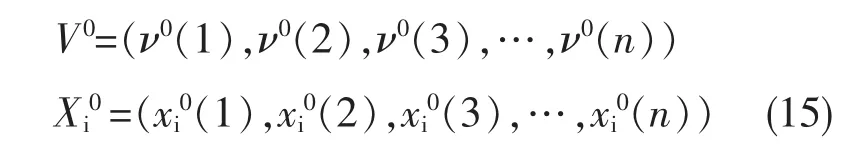
式中 V0=ν(k)-ν(1)

灰色绝对关联度ξi为

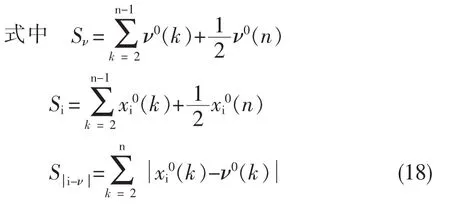
3.2 正交表建立及关联度分析
根据L9(34)规则表设置正交试验仿真参数,通过ANSYS/LS-DYNA仿真得到在不同参数组下破岩体积,建立如下表3。
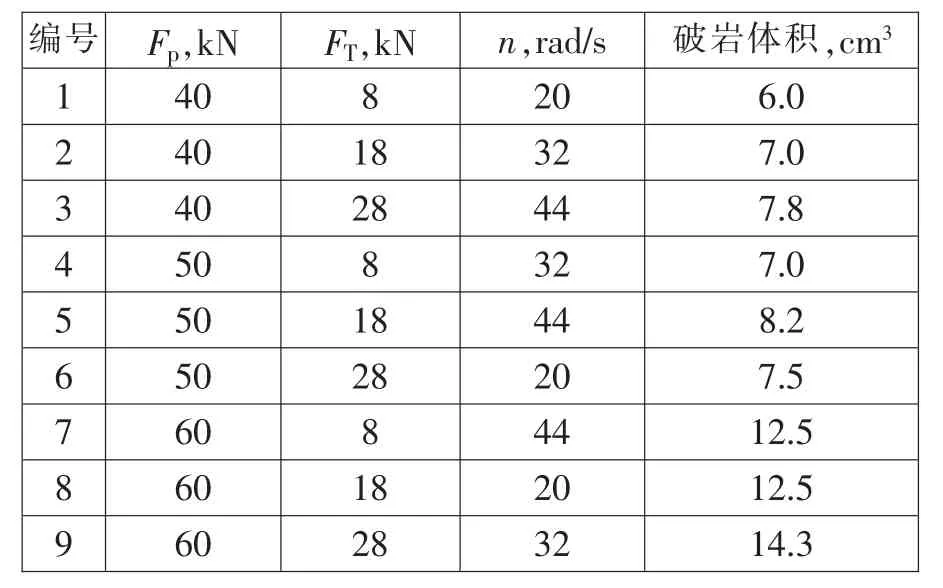
表3 工作参数正交试验表
将各因素如公式(15)初始化,绘制图6变化曲线。直观分析可知:冲击力变化曲线与破岩体积变化曲线的相似程度较高,转钎速度与轴推力变化曲线与破岩体积的相似程度较低。
计算各个特征因素的灰色绝对关联度,结果如表4。
由计算结果可知:冲击力与凿岩速度的关联性最大,其次是轴推力,关联性最小的是转钎速度。该计算结果与图6的曲线分析一致,因此具有较高可信度。

图6 初始化各因素的变化曲线

表4 特征因素灰色关联度值
4 实验研究
本实验采用中南大学机电工程学院与河南某公司联合开发的凿岩台车,该台车有两个机械臂,整机重量约45吨,可钻孔深为5.5m。配备某型国产凿岩机,并对该凿岩机进行改造,通过压力反馈式液压凿岩冲击控制方式,可实现冲击能、冲击频率、轴推力、转钎速度等工作参数的独立地、无级地调节,目前已完成样机研制,在隧道内进行工业性试验。该凿岩台车具有自适应寻优与固定工作参数两种工作模式,本文中采用固定工作参数的运行方法,在实验过程中手动调节工作参数值的大小。
实验目的:(1)验证冲击力、轴推力、转钎速度等工作参数是否存在最优值;(2)验证影响凿岩速度的敏感因素。
实验一:采用单一变量法进行最优值分析,依次改变其中一个工作参数进行试验,记录凿岩速度。每组工作参数重复3次,求取平均速度,对其进行数据分析。由公式(3)可知,冲击力与冲击能正相关,在此通过调整冲击能来表示冲击力的变化趋势。
由实验编号1、2、3可知,当轴推力与转钎速度不变时,冲击能增大,凿岩速度加快,因此冲击能无最优值。由实验编号4、5、6可知,当冲击能与转钎速度不变时,轴推力在18.8kN时,凿岩速度最快,因此轴推力存最优值。由实验编号7、8、9可知,当冲击能与轴推力不变时,转钎速度在31.4 rad/s时,凿岩速度最快,因此转钎速度存在最优值。该实验结果与理论分析一致,从而验证研究的准确性。

图7 凿岩实验现场

图8 凿岩过程监控画面
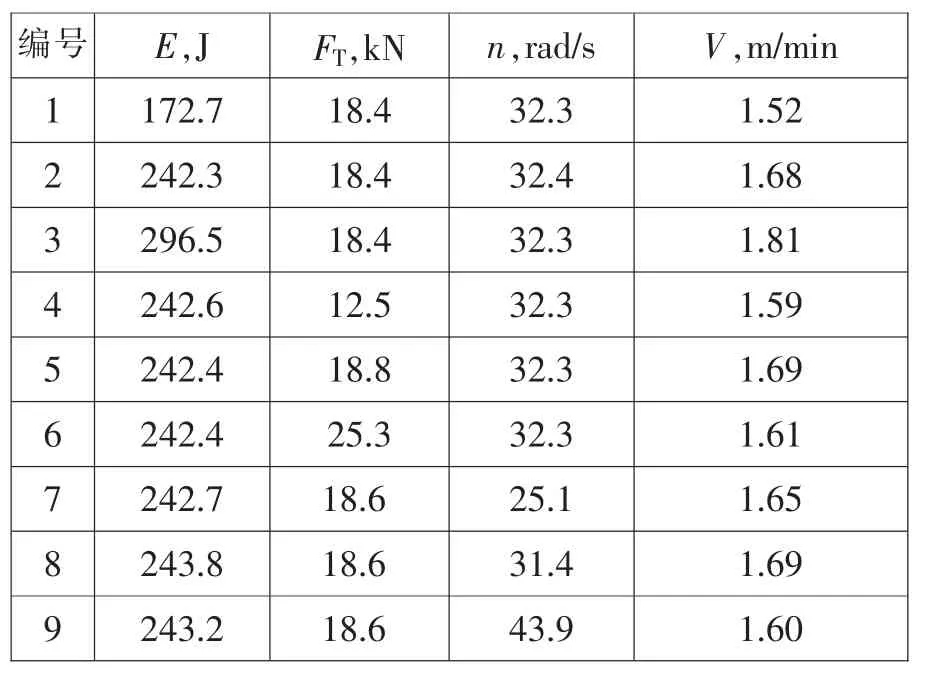
表5 最优值分析实验结果

表6 L9(34)正交规则试验结果
实验二:根据L9(34)正交表规则设定工作参数,依次进行凿岩试验,每组工作参数也重复3次,求取平均速度,对其进行数据分析,绘制表6。
采用3.1节计算方法求取冲击能、轴推力及转钎速度的灰色关联度值,结果依次为:0.69、0.65、0.63, 与仿真所得 0.78、0.64、0.60 相比较小,这是由于系统控制误差、传感器检测误差以及岩石性质差异共同造成,但整体趋势大致相同,其主次关系分别是:冲击能>轴推力>转钎速度。该实验结果与仿真结论一致。
5 结论
本文通过力学模型分析凿岩工作参数的最优值。可知:冲击力无最优值,冲击力越大,凿岩速度越快;轴推力、转钎速度存在最优值。基于ANSYS/LS-DYNA软件仿真,采用单一变量法验证理论分析的准确性,同时根据L9(34)正交规则表进行关联性仿真试验,计算灰色绝对关联度,得出冲击力对凿岩速度的影响最大,其次是轴推力,对凿岩速度影响最小的是转钎速度。最后,进行实验分析,验证了理论及仿真结果的准确性。本文的研究有助于充分认识各个工作参数对凿岩速度的影响,合理地设置工作参数。在凿岩施工中,可根据关联度分析影响钻进速度的原因,对于自寻优控制系统,可根据灰色绝对关联性值调节寻优步距系数,具有重要的参考意义。
参考文献:
[1]徐小荷,余静.岩石破碎学[M].北京:煤炭工业出版社,1984:159-180.
[2]LI Xibing,Summers D A,Rupert G.Experimental investigationon the breakage of hard rock by the PDC cutters with combined action modes[J].Tunneling and Underground Space Technology,2001,16:107–114.
[3]LONGRisheng,SUN Shaoni,LIAN Zisheng,LIAOYaoyao,QIN Xiaofeng.A new technology for hard-rock tunneling based on drilling and hydraulic impact breaking[J].International Journal of Mining Science and Technology,2015,25:1053-1058.
[4]刘德顺,李夕兵,杨襄壁.冲击机械系统的波动力学研究[J].机械工程学报,1997,33(4):104-106.
[5]Sekercioglu T.Failure study of pneumatic rock drill piston[J].Engineering Failure Analysis,2006,13(7):1108-1115.
[6]W.C.Zhu,C.A.Tang.Numerical simulation of Brazilian disk rock failure under static and dynamic loading[J].International Joural of Rock Mechanics&Mining Sciences,2006,43:236-252.
[7]L.E.Chiang,D.A Elia as.Modeling impact in down the hole rock drilling[J].International Joural of Rock Mechanics and Mining Sciences.2000,37:599-613.
[8]赖海辉,朱成忠,李夕兵等.机械岩石破碎学[M].长沙:中南工业大学出版社,1991.1-15.
[9]杨襄璧.液压凿岩机轴推力的计算[J].凿岩机械与风动工具,1982(1):1-5.
[10]高澜庆,刘庭楷,王保申,殷秋生.液压凿岩机主要工作参数对凿岩速度影响的试验研究[J].凿岩机械气动工具,1996(4):52-54.
[11]曹中一,李候清,罗前星 等.以LS-DYNA为基重型凿岩机冲击能的波动力学分析[J].现代制造工程,2010,(8):128-131.
[12]宫凤强,李夕兵,刘希灵.三维动静组合加载下岩石力学特性试验初探[J].岩石力学与工程学报,2011,(6):1179-1190.
[13]宋嘉宁,李琴,谭力 等.潜孔钻头破岩机理仿真研究[J].西南石油大学学报,2007,(29):113-115.
[14]范永涛,黄志强,高德利 等.物探冲旋钻头破岩机理仿真研究[J].石油钻探技术,2011(3):110-113.
[15]韩新平,侯成恒,邹伟.回转切削钻机凿岩速度影响因素的灰关联分析[J].应用泛函分析学报,2015(2):193-197.
[16]LIMancheng.Greyassessment of examination[J].The Journal of Grey System,1997,9(1):83-87.

