青岛崂山黑松立木结构特征模型
袁志超,张家盛,李士美,王永涛,崔孝平
(1.青岛农业大学 园林与林学院,山东 青岛 266109;2.青岛市林业局,山东 青岛 266061;3. 崂山区林业局,山东 青岛 266061)
立木结构特征决定着树干材积的数量和质量,是森林计测用表编制的基础,对森林资源调查、评估及经营管理都有着非常重要的意义。[1-3]森林计测常用的材积表主要为基于立木胸径、树高的一元材积表或二元材积表。然而,在林业资源管理部门处理盗伐案件以及处理林权纠纷中,经常要对被伐木材积做出估计。对于被伐木,能测定的基本特征因子只有地径,因而仅能通过对地径的测定间接推算胸径和树高,然后用立木材积表计算被伐木的材积。[4,5]因而,研究地径与胸径、树高的关系,构建合适的数学模型,在林业资源管理上有重要的现实意义。
近年来,无人机逐渐成为森林资源调查与监测的新手段,已应用于单木树高、胸径、冠幅等信息的获取以及森林信息量化等方面的研究。[6,7]无人机影像在森林结构参数提取方面主要包括单木树高、单木冠幅、株数密度、郁闭度、林分平均高、生物量及蓄积量等因子,然而树木胸径的获取主要是通过影像提取的树木高度和冠幅来进行反演。[8,9]由于胸径是立木结构特征的基本参数,确立胸径与树高、冠幅等结构参数的确切关系,是运用无人机对森林资源准确计测的前提和基础。
黑松(Pinusthunbergii)系日本第一次侵占青岛后引入的针叶树种,目前已经成为山东半岛的重要基调树种。然而,有关黑松立木结构特征参数的相关研究鲜有报道。[10]本研究通过黑松立木结构特征因子的实测,基于立木地径、胸径、冠幅、树高等特征因子的关系分析,构建黑松立木结构特征参数模型,以期为区域森林资源调查与监测、森林资源保护与管理等提供参考。
1 研究区概况
崂山位于山东半岛南部的黄海之滨,地处36°05′—36°19′ N,120°24′—120°42′ E,是中国海岸线第一高峰,主峰海拔1 132.7 m。崂山属暖温带季风气候,年平均气温11.9 ℃,年日照平均时数2 622.3 h,年平均降雨量约800 mm。崂山土壤的成土母岩主要是中生代花岗岩酸性岩类及喷发熔岩基性岩类,土壤多为棕色森林土,以沙壤为主。崂山自然植被属暖温带落叶阔叶林区,原以天然赤松林、栎类次生林为主,后经多年改造和更新造林,目前分布的主要森林类型为黑松林、赤松林、落叶松林、刺槐林、麻栎林以及部分杂木林和灌丛等。黑松林多分布于山地阳坡、半阳坡、低山丘陵直至海岸线。
2 材料与方法
选择无生长缺陷,树干生长正常,胸径大于5.0 cm的黑松作为样木。样木选定后,使用测径围尺测量地径(D0)、距地表10 cm直径(D0.1)和胸径(D1.3),运用布鲁莱斯测高器测量树高(H),用塔尺测量枝下高(h),用皮尺测量东西冠幅和南北冠幅(EW+NS)并计算其平均冠幅(CW)。共测定黑松样木191株,地径D0分布范围7.1~44.1 cm,胸径D1.3分布范围5.1~38.5 cm,树高H分布范围3.1~20.2 m。
首先,运用SPSS Statistics 19.0的相关分析功能,利用实测的191株样木数据,确定林木结构指标之间的相关关系。对191株样木数据进行整理抽样,按2 cm径阶进行整化,每个径阶按顺序抽3个隔1个进行回归模型的建立,遴选出建模样本144株,检验样本47株。然后,运用Origin Pro 8进行各指标之间的回归分析,构建各指标间的回归模型。拟合过程中,根据绘制模型预估值的标准残差图,将超出±2倍标准差以外的数据作为极端观测值予以剔除。原则上,选择调整的决定系数(Adj.R2)最大、残差平方和(RSS)和回归均方(MSR)最小的模型,作为最优树高曲线模型。运用SPSS Statistics 19.0配对样本t检验(Pair Sample t test)功能,对检验样本的实测值与各模型推算的理论值进行差异显著性检验,若检验结果t
3 结果与分析
3.1 各指标之间的相关性分析
相关分析结果表明(表1),在P=0.01水平(双侧)上,黑松立木结构的7个指标之间均存在极显著的正相关关系,其中以D0和D0.1的相关系数最大,其Pearson相关系数为0.986,其次为D0与D1.3,而h与WE的相关性相对较弱,其Pearson相关系数仅为0.531,但仍大于Pearson相关系数临界值0.185(P=0.01,df=190)。
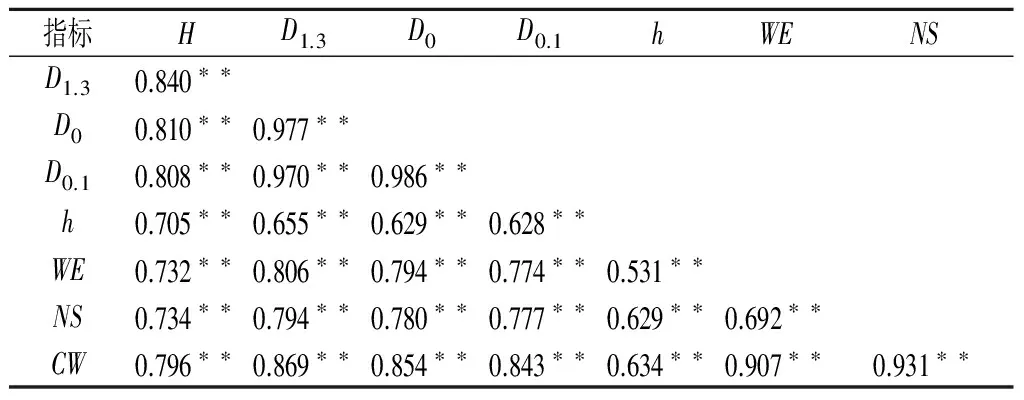
表1 黑松立木结构指标之间的相关性
3.2 不同部位直径之间的回归模型
D1.3-D0建模样木为144株,按照D1.3平均值±2倍标准差的标准未发现异常值。D1.3-D0之间的关系可以用线性式、指数式和逻辑斯蒂(Logistics)式等表示,其中逻辑斯蒂式的决定系数R2最小,为0.948 2,其他线性式和指数式的决定系数R2均为0.950 8(表2)。但线性式的RSS与MSR较小,且模型中所包含的参数较少,因而线性式是最优的拟合方程(图1)。模型预测精度检验结果表明,实测胸径与预测胸径的Pearson相关系数为0.982 5,差异显著性检验t=-0.475

表2 黑松D1.3-D0模型拟合结果比较
注:RSS-残差平方和,MSR-回归均方,下同

D1.3-D0.1建模样木为144株,按照胸径平均值±2倍标准差的标准未发现异常值。D1.3-D0.1之间的关系可用线性式、指数式和等表示。表3表明,在3种模型中,因多项式具有较小的RSS和MSR,且决定系数R2值较大,因而多项式的拟合优度最佳(图2)。对检验样本的实测胸径与预测胸径进行配对样本t检验,发现实测胸径与预测胸径的Pearson相关系数为0.969 6,差异显著性检验t=0.112 7

表3 黑松D1.3-D0.1模型拟合结果比较
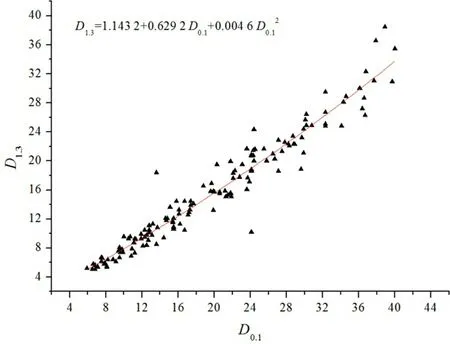
图2黑松D1.3-D0.1最优模型拟合及残差图
D0-D0.1建模样木为144株,按照胸径平均值±2倍标准差的标准未发现异常值。D0-D0.1之间的关系可用线性式、指数式和多项式等表示。表4表明,在3种模型中,因多项式具有较小的RSS和MSE,且决定系数R2值较大,因而多项式为描述D0-D0.1关系的最佳模型(图3)。对检验样本的实测胸径与多项式预测胸径进行配对样本t检验,发现实测胸径与预测胸径的Pearson相关系数为0.991,差异显著性检验t=-0.358 2

表4 黑松D0-D0.1模型拟合结果比较
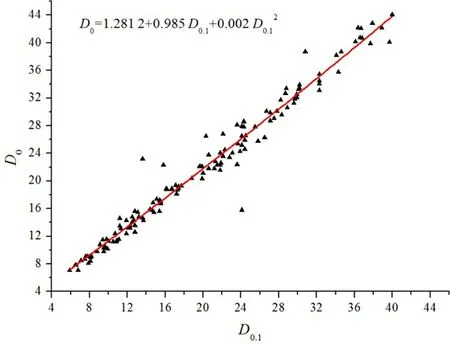
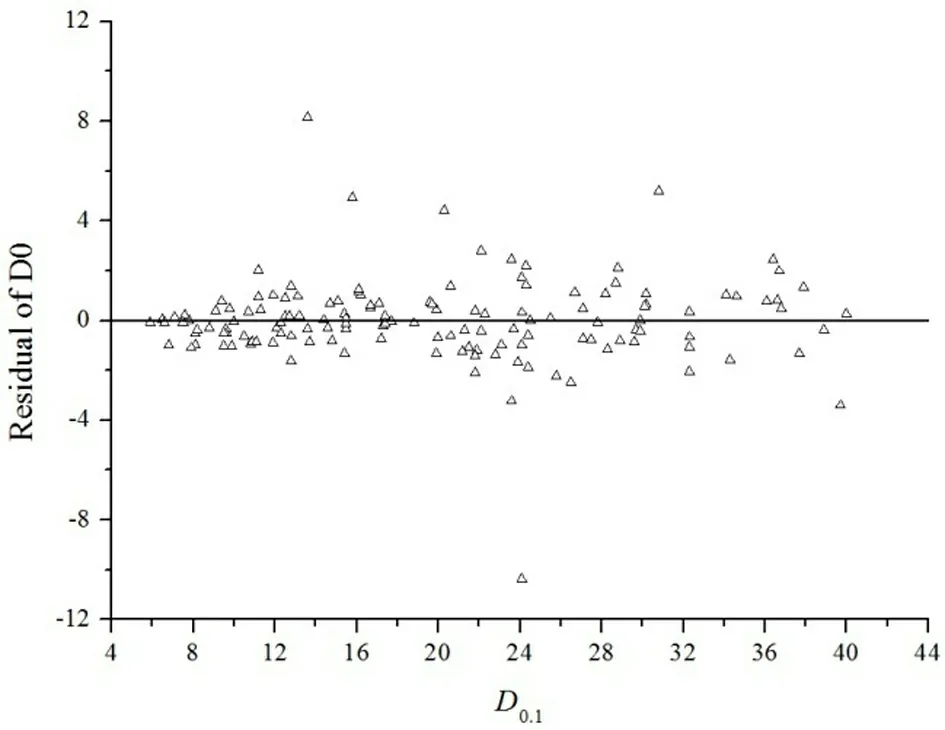
图3D0-D0.1最优模型拟合及残差图
3.3 胸径-树高相关关系分析
按照树高平均值±2倍标准差的准则剔除异常数据2株,最终保留142株黑松胸径树高数据用于建模。表5说明,D1.3-H之间的相关关系可用指数式、逻辑斯蒂(Logsitic)式和冈珀茨(Gompertz)式表示,其中指数式的拟合优度最佳,其决定系数R2为0.768 9,树高残差均在2倍标准差-5.859 8~5.859 8范围内(图4)。对检验样本的实测树高与指数式预测树高进行配对样本t检验,发现实测树高与预测树高的Pearson相关系数为0.872 9,差异显著性检验t=0.802 4

表5 黑松D1.3-H曲线拟合模型结果比较
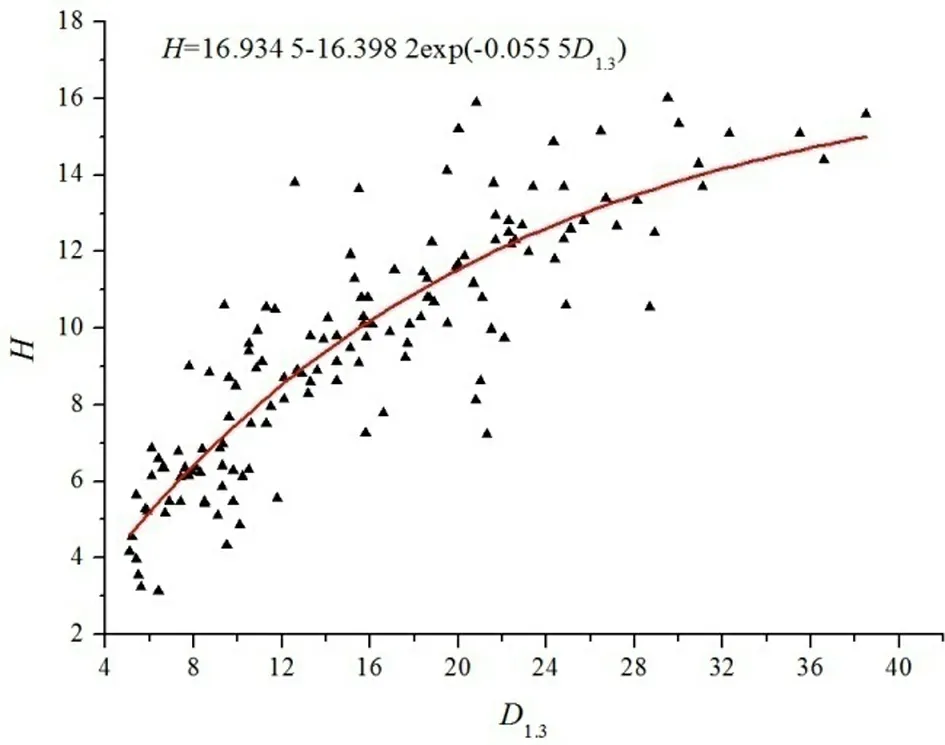
图4黑松D1.3-H最优模型拟合及残差图
3.4 胸径-冠幅相关关系分析
对建模样本的胸径-平均冠幅数据回归分析,发现线性式、指数式和多项式均能较好地反应二者之间的线性关系(表6)。由于线性式模型相对简单,且决定系数R2值较大,而RSS值与其他两个模型基本一致,因此线性式是反应D1.3-CW之间关系的最佳模型,残差图结果显示D1.3残差在2倍标准差即-15.335~15.335范围内(图5)。对47株检验样本的实测胸径与线性式预测胸径进行配对样本t检验,发现实测胸径与预测胸径相关系数为0.898 4,差异显著性检验t≈0

表6 黑松D1.3-CW曲线拟合模型结果比较

图5黑松D1.3-CW最优模型拟合及残差图
4 结论与讨论
立木结构特征是森林资源调查、评估及经营管理的基础,涵盖立木不同部位的直径、树高、冠幅、干形等指标和因子。本研究通过对191株黑松立木结构特征因子的实测,基于立木地径、胸径、冠幅、树高等特征因子的关系分析,构建了黑松立木结构特征参数模型。研究发现,黑松立木结构地径(D0)、距地面10 cm直径(D0.1)、胸径(D1.3)、树高(H)、枝下高(h)、冠幅(CW)等指标之间均存在极显著的正相关关系,其中以不同部位直径之间的相关性最强。
本研究拟合并比较了黑松立木结构指标之间的回归模型。首先,利用建模样本数据,分别拟合了3种常用的模型,通过比较决定系数R2、残差平方RSS和和回归均方MSR,筛选出拟合效果最佳的模型。然后,利用检验样本数据,对模型的拟合效果进行配对样本t检验,验证模型的预测效果。本研究发现,D1.3-D0、D1.3-D0.1、D0-D0.1之间的相关模型可分别用线性式、多项式和多项式表示,模型的决定系数R2分别为0.950 8、0.939 3和0.969 5。以往对针叶树种不同部位直径关系的研究结果也表明,胸径D1.3、地径D0之间存在显著的线性关系,如杉木地径D0与胸径D1.3间存在显著的线性关系[11,12]、沙地樟子松地径D0.1与胸径D1.3之间存在显著的多项式线性关系[13]。
由于树木生长受多种因素的制约,如树种生物学特性、立地条件、林分密度、管理措施等因素的影响,不同树种的胸径树高曲线模型存在较大差别,如七姊妹山黄杉胸径树高曲线为幂函数式[14]、帽儿山林场20个阔叶树种的胸径树高曲线模型分别为幂函数式、Schumacher式、单分子式、Richards式、Gompertz式和Logistic式等[15]。本研究黑松胸径树高(D1.3-H)之间的关系用指数式拟合优度最佳,决定系数R2为0.768 9,这与赤松的胸径树高模型比较一致[16],可能是由于两个树种在生物学特性比较相似。
利用无人机的航空摄影测量影像可以有效分析常绿森林的树冠结构,张凝等[17]利用的无人机的摄影测量影像分割方法,发现在快速获得单木冠幅信息的前提下冠幅提取精度达90.05%。然而,树木胸径数据无法直接测量,只能通过反演方法进行估测。本研究发现,黑松的胸径D1.3与冠幅CW之间存在显著的线性相关关系,其决定系数Adj.R2为0.805 8。检验样本的验证结果也表明,该模型能准确地反应胸径D1.3与冠幅CW之间的关系。
本研究基于191株样木的实测数据,通过拟合与比较分析,筛选出黑松立木结构特征参数模型。但是,由于未对样木所处的立地条件区别分类,如坡度、坡位、坡向等因子,对模型的预测精度有一定影响[18,19]。下一步的研究工作中,将不断丰富完善数据,把立地条件如坡度、坡向、海拔等因子与树木直径、树高和冠幅等结构指标联合建立估测模型来提高预测精度。
:
[1] Maltamo M,Mustonen K,Hyyppä J,et al. The accuracy of estimating individual tree variables with airborne laser scanning in a boreal nature reserve[J]. Canadian Journal of Forest Research,2004,34(9):1791-1801
[2] Weaver S A,Ucar Z,Bettinger P,et al. Assessing the Accuracy of Tree Diameter Measurements Collected at a Distance[J]. Croatian Journal of Forest Engineering,2015,36(1):73-83
[3] 姚爱静,朱清科,张宇清,等.林分结构研究现状与展望[J].林业调查规划,2005,30(2):70-76
[4] 闭海秀,黄清经.桂东区杉木地径与胸径、树高、材积相关分析[J].广西林业科学,2014(4):444-449
[5] 曾慎松.巨尾桉人工林地径与胸径、树高相关模型的研究[J].福建林业科技,2007,34(1):40-42
[6] 王伟.无人机影像森林信息提取与模型研建[D].北京:北京林业大学,2015
[7] 李祥,郑淯文,戴楚彦,等.基于无人机影像的森林信息获取研究进展[J].世界林业研究,2017,30(4):41-46
[8] 李亚东,冯仲科,明海军,等.无人机航测技术在森林蓄积量估测中的应用[J].测绘通报,2017(4):63-66
[9] 刘清旺,李世明,李增元,等.无人机激光雷达与摄影测量林业应用研究进展[J].林业科学,2017,53(7):134-148
[10] 许景伟,李传荣,李琪,等.沿海黑松防护林立木材积表的编制[J].山东林业科技,2003(4):22-25
[11] 王金荣.杉木天然林林木地径与胸径的关系研究——以福建五一国有林场为例[J].林业资源管理,2015(3):121-124
[12] 曾伟生.利用误差变量联立方程组建立南方杉木一元立木材积模型和胸径地径回归模型[J].中南林业调查规划,2012,31(4):1-4
[13] 张日升,刘广,于洪军,等.辽西北沙地樟子松地径与胸径相关关系及其应用研究[J].防护林科技,2006(3):19-21
[14] 熊斌梅,汪正祥,李中强,等.七姊妹山自然保护区黄杉年龄胸径树高的相关性研究[J].林业资源管理,2016(4):41-46
[15] 王小明,李凤日,贾炜玮,等.帽儿山林场天然次生林阔叶树种树高-胸径模型[J].东北林业大学学报,2013(12):116-120
[16] 徐悦,陈昌华,蒋之富,等.天然赤松胸径与树高相关模型的研究[J].林业调查规划,2008,33(3):56-58
[17] 张凝,冯跃文,张晓丽,等.结合航空影像纹理和光谱特征的单木冠幅提取[J].北京林业大学学报,2015,37(3):13-19
[18] 袁晓红,李际平.杉木人工林南北坡向树高-胸径生长曲线研究[J].西北林学院学报,2012,27(2):180-183
[19] 杜纪山,李希菲.杉木树高曲线参数稳定性的研究[J].林业科学研究,1998,11(2):169-174

