应用PTV粒子追踪测速技术的鱼卵运动试验研究

刘雪飞，林俊强，彭期冬，余 康，陈永灿，3，庄江波

（1.中国水利水电科学研究院， 北京 100038；2.清华大学 水沙科学与水利水电工程国家重点实验室，北京 100084；3.西南科技大学 环境与资源学院，四川 绵阳 621010）

1 研究背景

鱼卵的漂流运动和自然降河过程，是鱼类早期发育的重要阶段。1960年代，易伯鲁［1］根据鱼类早期资源（卵、苗）调查提出的产卵规模和产卵场位置估算方法仍沿用至今。该方法主要通过采样断面的江水平均流量、少数采样点的卵苗平均密度来估算产漂流性卵鱼类的产卵规模，通过采集到卵苗的发育时间和江水平均流速，反推上游产卵场位置。然而，由于河道地形不同，必然导致各江段流速分布不同、卵苗断面分布不均，由此估算的产卵规模可能在实际产卵规模的1～2个数量级以下［2］，估算的产卵场范围往往在20～40 km［1］，有些甚至达70 km［3］，估算结果存在随意性大、准确性差、可靠性低等问题。另一方面，鱼卵漂流运动关系着鱼类的成功孵化和资源补充。1980年代以来，我国开始大量兴建水库，拦河大坝除了阻隔鱼类洄游通道外，还改变了鱼卵的漂流条件，导致鱼卵在库区内的漂程和漂流时间不足，在孵化前于库区的缓流或死水区沉底死亡。能否通过水库调度或库区栖息地局部地形改造等手段，在有限漂程内为鱼卵创造不沉底水流条件，增加鱼卵在水中的悬浮和漂流时间，改善鱼卵的漂流孵化条件，一直是鱼类保护工作者思考的问题。虽然，该问题悬而未解，但鱼卵运动研究是解答这一问题的力学基础。可见，鱼卵运动研究对鱼类早期资源估算和产卵场位置推算，乃至鱼类栖息地修复等方面研究都具有重要意义。

目前，鱼卵运动特性研究多通过野外调查和野外试验进行［4］，然而野外环境复杂、影响因素众多和环境变量不可控，使得研究成果多偏于定性，缺乏定量化和机理性成果。在室内可控条件下进行重复性机理试验是定量研究鱼卵运动规律的有效手段。然而这方面的室内试验，国内外也仅见零星报道。例如，唐明英等［5］应用水槽试验，通过鱼卵分层采集测定“四大家鱼”鱼卵直线运动20 m后的断面分布情况，研究了鱼卵断面分布、鱼卵悬浮率与流速之间的响应关系，得出鱼卵安全漂流的下限流速为0.25 m/s。罗佳等［6］在均匀流场条件下，通过视频录像记录匙吻鲟和达氏鳇两种鲟鱼卵在水槽中的运动轨迹，拟合了两种鲟鱼卵漂流轨迹与流速的定量关系式。Garcia等［7］通过视频定量观测了人工合成鱼卵在不同流速、不同河床形态下的运动轨迹，发现在小流速（＜0.056 m/s）工况下，鱼卵容易在沙波背水面沉陷，而在较大流速（≥0.056 m/s）工况下，鱼卵会在沙波表面跳跃甚至翻滚过沙波顶部。尽管这些试验对鱼卵运动展开了初步的量化研究，但多为阐明现象，对鱼卵漂流速度、沉降速度、运动轨迹特性及其影响因素等问题仍没有系统解答。

鱼卵在水体中受自身重力、浮力、水流拖曳力、惯性力和压力梯度力等共同作用下随流运动，和泥沙颗粒一样可视为固液两相流中的颗粒运动。虽然鱼卵大小、比重与泥沙颗粒在量级上有着显著区别，且鱼卵大小、比重会随着生长发育而变化的特殊生物属性，使其运动规律与泥沙运动规律存在差异，但是在实际研究中可借鉴泥沙运动方面的先进试验手段和分析方法，如粒子追踪测速（Particle Tracking Velocimetry，PTV）技术，该技术具有追踪测量大量颗粒速度，逐一识别颗粒运动轨迹的显著优势，已广泛应用于泥沙机理试验中［8-10］。本文通过系列水槽试验，应用PTV技术定量测量鱼卵在不同流速、不同水深等工况下的粒子速度和运动轨迹，并对鱼卵受力条件进行适当概化，解析推导鱼卵运动方程，探究不同水流条件下的鱼卵漂流运动规律。

2 试验方法

2.1 水槽系统 试验在一自循环水槽系统中开展，该系统包括进口喇叭段、直线段、出口突扩段、稳流栅、尾门和移动测量平台等结构，水槽侧面为玻璃边壁，底部为大理石壁面。水槽直线段长14 m，宽0.8 m，高0.8 m，断面为矩形，底坡为平坡。为创造近似均匀流条件，减小进口喇叭段水流影响，鱼卵运动试验在水槽直线段的后半段进行。在水槽直线段中间位置设置鱼卵投放断面，在水槽顶部移动测量平台上架设一L型漏斗，避免每次鱼卵投放时垂向初速度不同对鱼卵运动的干扰。在投放断面下游4 m范围内设置鱼卵运动观测段，在观测段内架设PTV测量系统。试验水槽系统及设备布置如图1所示。

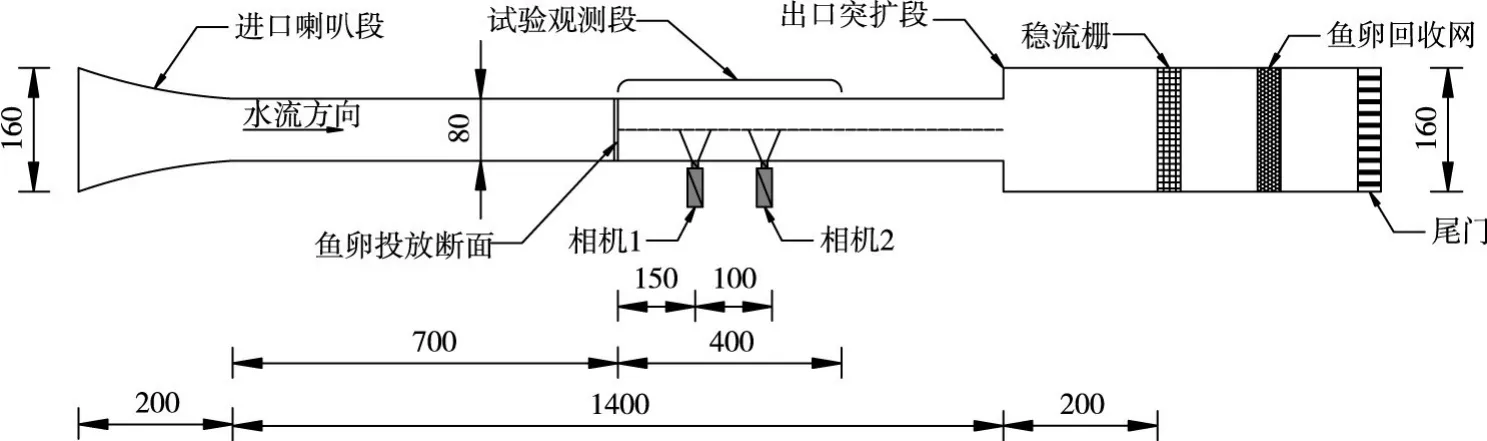
图1 水槽及PTV系统布置（单位：cm）

2.2 PTV系统 PTV粒子图像测速系统由图像采集系统和图像处理系统构成。图像采集系统由2台1600万像素的运动相机、面光源和增光背景组成。2台运动相机紧贴水槽一侧玻璃边壁架设，且保持相机镜头水平，面光源架设于相机同侧，在水槽另一侧和底部覆盖白色防水背景纸以布设增光背景，同时可减小另一侧玻璃壁面透光和反光影响。图像处理系统包括帧图像提取模块、畸变校正模块、灰度转化模块、粒子识别模块和像素-速度校正模块，处理程序在matlab工具包-PTVlab［11］的基础上改编，可实现粒子运动速度、运动轨迹和轨迹特征（如轨迹坡度）的统计分析。

2.3 试验材料、工况和操作 试验采用一种订制的海藻酸钠聚合物作为模型鱼卵材料，模型鱼卵平均粒径为4.0 mm，相对比重为1.01，与天然四大家鱼鱼卵物理性状相似（四大家鱼鱼卵充分吸水后平均卵径为 4.0～5.3 mm［12］，相对比重为1.0014～1.0031）［5］，为与白色背景形成鲜明对比、增强拍摄效果，特订制黑色模型鱼卵。该材料具有安全无毒、性状稳定、便于染色、可重复利用和漂流性良好等特点，可克服真卵不易保存、脆弱易损、染色缩水、透明不利于观测和难以重复利用等缺点。

本文共进行了不同水深和不同流速共计20组工况试验，试验基本参数如表1所示。每组工况试验时，通过控制变频泵频率和下游尾门开度，调节水槽流量和水位至预设工况水平，待流态稳定形成近似均匀流后，应用旋浆流速仪测量观测段内的流速，而后在鱼卵投放断面的中间位置投放定量模型鱼卵（50 ml，约2000粒），应用相机软件平台开启2台相机，以每秒120帧的频率同步记录鱼卵运动过程。每组工况各投放5次模型鱼卵，重复进行5次鱼卵运动试验，2个相机记录10组运动轨迹视频。20组工况共计获得200组视频数据。

表1 试验工况及水流基本参数

3 鱼卵运动特性分析

3.1 鱼卵运动速度特性 鱼卵在投放断面中间位置释放后，一边随着水流沿纵向运动，一边受紊流作用沿横向扩散。鱼卵进入相机观测范围内，将在水槽中线附近形成一定宽度的粒子条带。流速越慢，鱼卵到达两个观测相机的粒子条带宽度越大。距离相机镜头越近的粒子，在图像中的像素点越大，测得粒子速度将高估，反之亦然。为了减小粒子距离镜头过远或过近造成粒子速度的测量误差，本文通过设置图像粒子的识别像素阈值，仅识别水槽中线附近（中线5 cm宽度范围内的粒子条带）的鱼卵粒子，并统计鱼卵纵向速度up1和垂向速度up2在不同区间内的频率分布。以工况9为例（流速uf=0.35 m/s），鱼卵纵向速度的频率分布如图2中的直方图所示。

图2 工况9鱼卵纵向速度的频率分布

从图2可以看出，同一水流条件下鱼卵纵向速度呈近似正态分布（鱼卵垂向速度分布也有相同规律），该结果服从多数自然统计规律。进一步地，应用标准正态分布函数拟合鱼卵速度的频率分布直方图，计算正态分布函数的均值（下标i=1表示纵向分量，i=2表示垂向分量），即为该工况相机1第1组视频中大多数鱼卵粒子的平均速度水平。在同一工况下，对比两个相机5组重复试验的10组视频分析结果，鱼卵速度的频率分布规律相同（均为正态分布），且10组统计均值的差异检验表明两个相机不同重复试验的分析结果间无显著性差异，因此本文取10组视频分析结果的平均值作为该工况下鱼卵速度的平均水平。不同水深、不同流速工况下，鱼卵纵向和垂向的平均速度统计结果如图3。从图3（a）中可以看出，在相同水深不同流速条件下，鱼卵纵向速度随着水流纵向速度的增大而增大，且两者呈线性关系，在相同流速不同水深条件下，鱼卵纵向速度的几组标记点几乎重叠，表明水深对鱼卵纵向速度的影响较小。鱼卵纵向速度与水流纵向速度间几乎遵循同一线性关系，应用up1=auf关系式进行趋势线拟合，可得线性关系式的斜率系数a=0.73，表明鱼卵纵向速度为水流纵向速度的0.73倍，滞后于水流纵向速度。从图3（b）中可以看出，在相同水深不同流速条件下，鱼卵垂向速度上下波动，在相同流速不同水深条件下，鱼卵垂向速度也上下波动，可见水深和水流纵向速度对鱼卵垂向速度的影响较小。几乎所有工况的鱼卵垂向速度均围绕在-0.008 m/s这一均值水平上下波动。值得注意的是，在水流纵向速度达0.93 m/s（工况20）时，该工况下的鱼卵纵向速度和垂向速度标记点均显著偏离趋势线，表明当流速达到一定值后，鱼卵粒子可能呈现出不同的运动规律。

图3 不同工况下鱼卵速度分布

3.2 鱼卵运动轨迹特性 在帧图像鱼卵粒子识别的基础上，对不同鱼卵粒子的运动轨迹进行连续追踪，可得一系列运动轨迹曲线。以工况9相机1拍摄的第1组视频为例（流速uf=0.35 m/s），其识别出的鱼卵运动轨迹曲线如图4所示。从图4可以看出，绝大部分的鱼卵粒子轨迹呈线性下降趋势，应用y=sx+b关系式拟合每个鱼卵粒子的轨迹曲线，并统计鱼卵粒子轨迹斜率s在不同区间的频率分布如图5中的直方图所示。从图5中可以看出，该视频中鱼卵轨迹斜率也呈正态分布规律，同样地，应用标准正态函数拟合轨迹斜率的频率分布直方图，并计算正态分布函数的均值，来表征该视频大多数鱼卵粒子轨迹斜率的平均水平。在同一工况下，2个相机5组重复试验下的10组视频分析结果间无显著差异，现取10组视频分析结果的平均值作为该工况下鱼卵轨迹斜率的平均水平。不同水深、不同流速工况下，鱼卵运动轨迹的平均斜率统计结果如图6所示。从图6可以看出，在相同水深不同流速条件下，鱼卵轨迹斜率的绝对值随着水流纵向速度的增大而减小，且具有一定的渐近趋势，即水流纵向速度越大，鱼卵轨迹的下降趋势越缓。在相同流速不同水深条件下，鱼卵轨迹斜率的几组标记几乎重叠，表明水深对鱼卵运动轨迹的影响较小。用指数函数拟合所有试验工况下水流纵向速度与鱼卵轨迹斜率的关系，可得s=-0.02-0.41exp（-11.20uf），R2=0.84。从拟合的曲线可以看出，当水流纵向速度超过某一临界值时，鱼卵轨迹斜率变化趋缓，鱼卵相对不易下沉，在本文试验条件下（uf=0.16～0.93 m/s），鱼卵轨迹斜率s趋于-0.02；当低于该临界速度时，鱼卵轨迹斜率迅速趋陡，鱼卵相对容易下沉。若假定轨迹斜率的变化率小于20%（即轨迹斜率的一阶导数s′≤0.2），所对应的流速为鱼卵不易下沉的临界流速，则应用拟合公式可求得该临界流速为0.28 m/s，与唐明英［5］报道的临界流速0.25 m/s相当；若假定轨迹斜率的变化率小于10%所对应的流速为鱼卵不易下沉的临界流速，则该值求得为0.34 m/s。

另一方面值得注意的是，当水流纵向速度增大到0.93 m/s时（工况20），鱼卵运动轨迹曲线表现出与较小流速工况截然不同的形态，如图7所示。鱼卵粒子轨迹已从简单的斜线式下沉，转变为波浪翻滚式下沉，且个别鱼卵会猝发式跃移，水流紊动效应对鱼卵运动的影响变得显著。

图4 工况9鱼卵线性下降运动时的轨迹

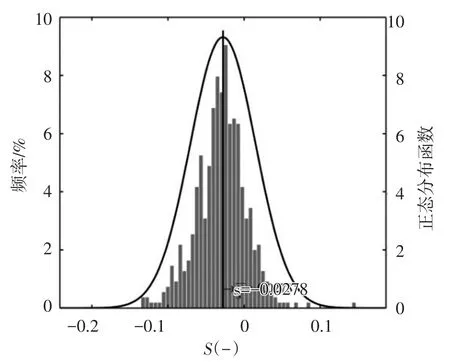
图5 工况9鱼卵轨迹斜率的频率分布

图6 不同工况下鱼卵轨迹斜率分布

图7 工况20鱼卵翻滚运动时的轨迹

4 讨论

4.1 鱼卵运动的理论推导 为了进一步分析鱼卵纵向速度、鱼卵沉速、鱼卵漂流距离和水流流速、鱼卵比重及鱼卵颗粒大小之间的定量关系，本文在直线水槽试验的基础上，对鱼卵运动问题进行如下概化：（1）仅考虑鱼卵受到水流不同方向拖曳力和自身有效重力的作用；（2）暂不考虑鱼卵旋转引起的Magnus力、流体剪切作用引起的Saffman力、鱼卵附加质量力、Basset力、压力梯度力和水流紊动的作用。鱼卵运动的概化及受力分析如图8所示。

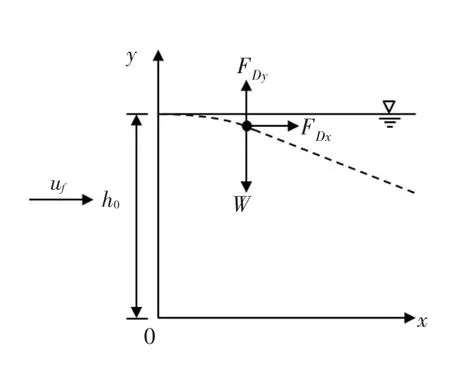
图8 鱼卵运动的概化和受力分析

水流拖曳力沿纵向（x方向）的合力FDx：

鱼卵有效重力W：

水流拖曳力沿垂向（y方向）的合力FDy：

式中：ρf为水流密度；ρp为鱼卵颗粒密度；dp为鱼卵粒径；uf1、uf2分别为x方向和y方向的水流速度；up1、up2分别为x方向和y方向的鱼卵颗粒速度；g为重力加速度；CD1为鱼卵颗粒沿x方向的拖曳力系数（沿x方向的形状阻力系数，与x方向鱼卵颗粒与水流的速度差|uf1-up1|有关）；CD2为鱼卵颗粒沿y方向的拖曳力系数（沿y方向的形状阻力系数，与y方向鱼卵颗粒与水流的速度差|uf2-up2|有关）。

根据式（1）—式（3）的受力分析，利用牛顿第二定律F=ma，列出鱼卵颗粒的运动方程可得：

式中：upi、ufi分别为鱼卵粒子速度（i=1为纵向，i=2为垂向）；gi为重力加速度分量；CDi为不同方向的拖曳力系数。

假设鱼卵从距离河床h0的高度位置处释放，t=0时刻鱼卵x方向的初始速度等于up10，y方向上的初始速度为up20，则鱼卵运动方程的初始条件可表达为：

本文根据Morsi等［12］提出圆球拖曳力系数（形状阻力系数）的分段拟合公式，CDi可表示为如下通用形式：

表2 不同鱼卵粒子雷诺数下的拟合常数值［13］

将式（6）、ReDi的表达式分别代入式（4），并令Ui=ufi-upi，可将式（4）及其初始条件式（5）简化整理为如下形式：

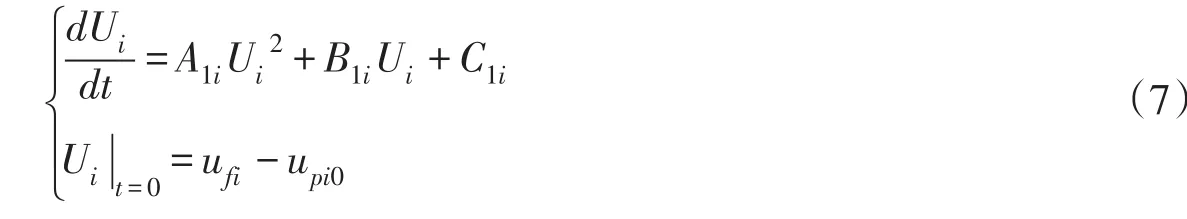
其中，

则本文鱼卵运动问题可简化为Riccati常微分方程的求解问题。当0.1＜ReDi＜5000，（通常情况下鱼卵粒子的雷诺数ReDi都处于该区间），可求解得式（7）的解析解为：

其中：

当ReDi＜0.1时，式（7）退化为：

其解析解为：

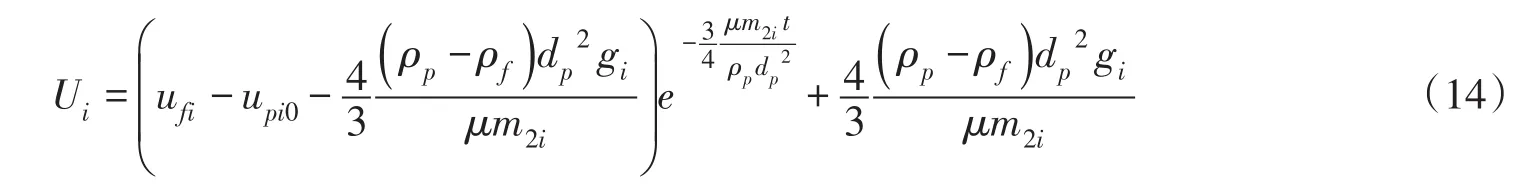
将m2i=24代入式（14）可得：

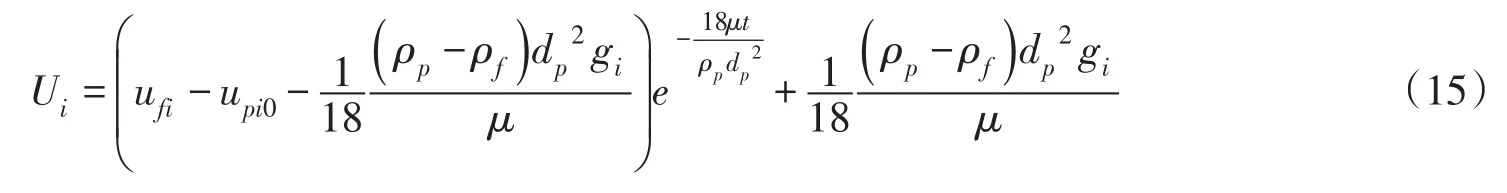
从式（9）、式（15）的表达式可以看出，鱼卵-水流相对速度Ui为时间t的函数，且具有渐近趋势，当t趋于无穷时，可得下式：

本文推导所得的鱼卵粒子速度公式具有显式表达式，可见鱼卵运动与水流速度、鱼卵比重、鱼卵粒径和鱼卵拖曳力系数（形状阻力系数）之间的复杂关系。另一方面，鱼卵运动研究主要关注鱼卵在主流区的输移特性，除地形边界附近流速梯度较大的区域和水流加速度较大的区域外，压力梯度力、附加质量力、Magus力、Saffman力和Basset力的作用都很小［14-15］，因此本文考虑拖曳力和有效重力作用所推导的理论公式，可适用于主流区大部分情况的鱼卵运动计算。在已知流场速度分布的数值计算中，可应用式（9）和式（14）直接计算鱼卵粒子速度，免去迭代求解式（4）运动方程的过程，可大幅提高鱼卵粒子速度和轨迹的计算效率。

此外，在天然河流中，水流受河道地形影响，具有沿河道纵向、横向和垂向的速度分量，将对鱼卵产生3个方向的拖曳力，鱼卵在纵向和横向上主要受水流拖曳力作用，而在垂向上主要受水流拖曳力和鱼卵有效重力共同作用，因此本文推导的理论公式中关于鱼卵纵向速度的分量公式可拓展到三维数值计算中鱼卵横向速度的计算。在三维情况下，鱼卵受横向流速的影响及作用机理与纵向相似。

4.2 鱼卵运动的影响因素及作用机理分析 从推导的鱼卵粒子速度公式（式（9）、式（15））可以看出，鱼卵运动主要和水流流速、鱼卵比重、鱼卵粒径和鱼卵初始速度等因素有关，因此，本文结合理论推导和试验结果着重分析这些因素对鱼卵运动的影响及其作用机理。

（1）水流流速。从式（16）中可以看出，水流纵向速度主要影响鱼卵纵向速度（漂流速度），鱼卵垂向速度则与水流纵向速度无关，这一理论推导结果与本文试验工况下的分析结果基本吻合。为了进一步分析水流流速对鱼卵速度和运动轨迹的作用机理，应用式（16）求解本文模型鱼卵材料（相对比重γp=1.01，dp=4.0 mm，）的理论纵向速度、垂向速度和轨迹斜率（鱼卵垂向速度与纵向速度比值），并将求得的理论曲线绘于相应的试验结果图中，如图9所示。从图9中可以看出，理论推导与试验分析两种方法得出的鱼卵运动与水流流速的趋势关系相同，但在趋势值上有所不同，具体表现在理论上鱼卵纵向速度趋于水流纵向速度，而试验上鱼卵纵向速度的趋势值仅为水流纵向速度的0.73倍，滞后于水流纵向速度（图9（a））；理论上鱼卵垂向速度趋于-0.021 m/s，而试验上鱼卵垂向速度趋于-0.008 m/s（图9（b）），试验鱼卵稳定沉速小于理论估计沉速（沉速一般指向下垂向速度的数值）；在本文试验的0.16～0.93 m/s速度变化范围内，理论估算的鱼卵轨迹下降趋势均有所高估，试验上不同流速条件下鱼卵运动轨迹斜率均较理论估算的偏缓（图9（c））。整体而言，鱼卵运动的理论公式对鱼卵纵向速度、沉速和轨迹陡率都有所高估，表明水流流速除了在速度大小上对鱼卵运动产生影响外，还有水流流速引起的其他效应影响鱼卵运动。笔者推断造成该差异的主要原因是理论公式未考虑紊流作用。在紊流中，水流流速在不同方向上产生的紊动可能在鱼卵运动方向上产生了附加阻力效应，从而减小鱼卵的漂流速度（鱼卵纵向速度）和沉速，也减缓鱼卵在水流中的下沉趋势。

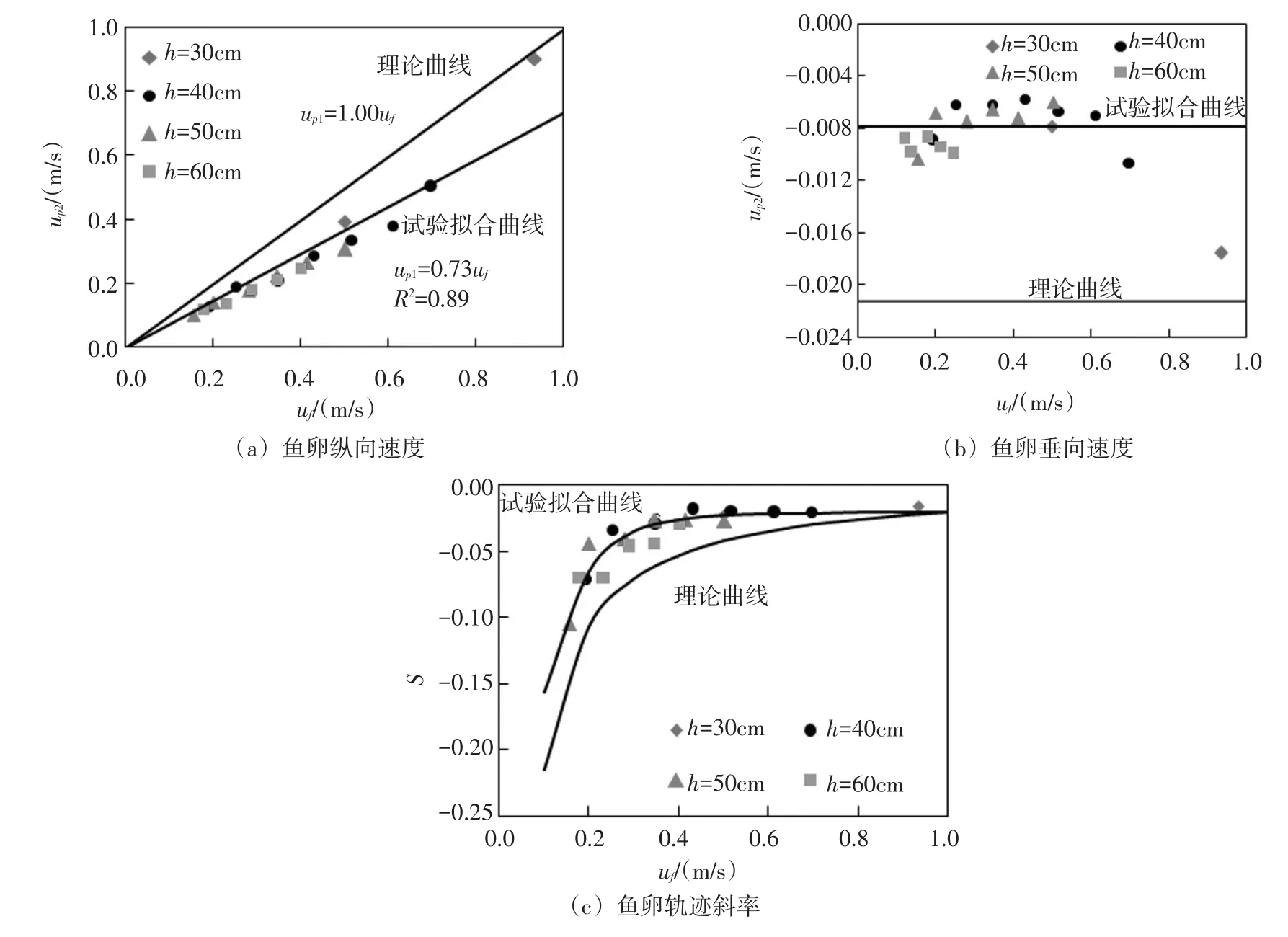
图9 鱼卵运动的理论与试验拟合曲线对比

（2）鱼卵比重和粒径。从式（16）可以看出，鱼卵比重和粒径主要影响鱼卵沉速（垂向速度），而鱼卵沉速对于产漂流性卵鱼类（如四大家鱼）而言是判别鱼卵是否有沉底风险的重要参数，对于产沉性卵鱼类（如中华鲟）而言也是研究鱼卵沉底前漂流散布特性的参考依据。为了进一步揭示鱼卵比重和粒径对鱼卵沉速的作用机理，应用式（16）计算了不同鱼卵比重和粒径下鱼卵沉速的变化曲线，如图10所示。图10中4条曲线分别是根据假定的4个不同鱼卵比重（γp=1.5、1.05、1.01、1.001）和10个不同鱼卵粒径（dp=1～10 mm）［4，16-17］计算而得，鱼卵比重和粒径范围可表征大多数鱼类的鱼卵物理属性，例如γp=1.001的曲线可代表与四大家鱼卵比重近似的鱼卵沉速曲线（四大家鱼鱼卵相对比重为1.0014 ～ 1.0031［5］），γp=1.5的曲线可代表与中华鲟卵比重近似的鱼卵沉速曲线（据长江水产研究所实测数据显示，中华鲟鱼卵相对比重为1.105～1.792）。从图10中可以看出，鱼卵比重越大，鱼卵沉速越大，鱼卵比重对鱼卵沉速的作用较为显著。相同比重下鱼卵沉速与粒径的变化曲线在双对数坐标系中呈近似线性关系，表明鱼卵粒径对鱼卵沉速的作用关系近似为指数函数关系。当鱼卵比重较小时，鱼卵沉速曲线的斜率相对较陡，表明该情况下鱼卵粒径变化对鱼卵沉速的影响更为显著。

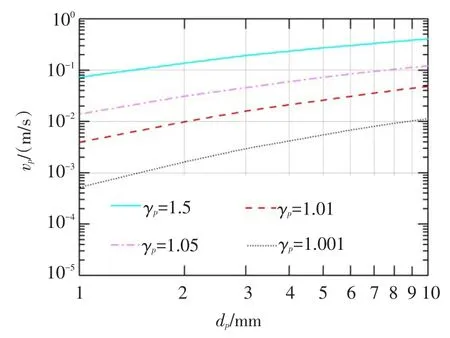
图10 不同鱼卵比重和粒径下鱼卵沉速的变化曲线

（3）鱼卵初始速度。鱼卵速度的计算首先是根据初始时刻鱼卵速度和水流速度的差值|ufi-upi0|计算鱼卵粒子的初始雷诺数ReDi0，再根据鱼卵雷诺数的大小确定m1i、m2i、m3i系数，即可应用式（9）和式（15）计算得出下一时刻鱼卵运动速度和运动位置，而后根据该时刻位置的流速和鱼卵速度，进一步推算下一个时刻的鱼卵运动速度和运动位置，如此往复，可计算鱼卵每一时刻的速度和运动轨迹。从鱼卵速度公式的表达式可以看出，鱼卵速度与水流速度的差值Ui随着时间的推移具有渐近趋势，趋于某一定值。为直观揭示鱼卵初始速度对鱼卵速度和轨迹的作用机理，假设3组不同鱼卵速度初值工况（工况a：up10=0，up20=0；工况b：up10=0.4m/s，up20=-0.2m/s；工况c：up10=0.8m/s，up20=-0.4m/s；3组工况的水流条件、鱼卵比重和粒径相同，uf1=0.5m/s，γp=1.01，dp=4mm），应用鱼卵粒子速度公式（式（9）、式（15）），计算并绘制鱼卵纵向速度、垂向速度和运动轨迹的变化曲线，如图11所示。从图11（a）（b）可以看出，鱼卵初始速度对鱼卵纵向速度和垂向速度的影响仅在初始极为短暂的时间内（1s内），鱼卵纵向速度迅速趋于稳定漂流速度，鱼卵垂向速度迅速趋于稳定沉速。而鱼卵速度初值对鱼卵运动轨迹的影响也仅在初始较短的距离内，轨迹斜率迅速趋于相同定值（图11（c））。

图11 鱼卵初始速度对鱼卵运动的影响

5 结论

本文通过20组不同水深、不同流速工况的水槽试验，应用PTV技术测量模型鱼卵粒子的速度和运动轨迹，并由鱼卵运动方程解析推导鱼卵速度公式，系统分析了恒定均匀流条件下鱼卵运动特性、主要影响因素及其作用机理，得到如下主要结论：（1）鱼卵纵向速度随水流纵向速度的增大而增大，两者呈线性关系，鱼卵纵向速度的试验拟合结果为水流纵向速度的0.73倍，鱼卵垂向速度与水流纵向速度无直接显著关系，在均值-0.008 m/s附近波动。（2）在流速较小工况下，鱼卵运动轨迹呈线性下降趋势，运动轨迹斜率随着流速增大而趋缓。当流速增大到0.93 m/s时，鱼卵轨迹从简单的斜线式下沉，转变为波浪翻滚式下沉，且个别鱼卵会猝发式跃移，水流紊动效应对鱼卵运动的影响变得显著。驱使鱼卵发生不同形式运动的临界流速，以及水流对鱼卵的紊动效应还有待进一步研究。（3）鱼卵运动的主要影响因素为水流速度、鱼卵比重、鱼卵粒径和鱼卵初始速度。（4）水流纵向速度主要影响鱼卵纵向速度（漂流速度），鱼卵运动理论公式对鱼卵纵向速度、沉速和轨迹斜率都有所高估，这种差异表明水流流速除了在速度大小上对鱼卵运动产生影响外，还有水流流速引起的紊动效应影响鱼卵运动。在紊流中，水流流速在不同方向上产生的紊动可能在鱼卵运动方向上产生了附加阻力效应，从而减小鱼卵的漂流速度和沉速，也减缓鱼卵在水流中的下沉趋势。（5）鱼卵比重和粒径主要影响鱼卵的垂向速度（沉速），鱼卵比重对鱼卵沉速的作用较为显著，鱼卵粒径对鱼卵沉速的作用关系近似为幂函数关系。当鱼卵比重较小时，鱼卵沉速曲线的斜率相对较陡，表明该情况下鱼卵粒径变化对鱼卵沉速的影响更为显著。（6）鱼卵纵向速度与垂向速度均为时间t的指数函数，且随着时间推移具有渐近趋势，鱼卵初始速度对鱼卵纵向速度和垂向速度的影响仅在初始极为短暂的时间内。（7）本文推导的鱼卵速度理论公式具有显式表达式，可使读者洞见鱼卵运动与其影响因素之间的复杂关系，且具有一定的通用性，可推广应用于求解流场后的鱼卵运动数值计算中，免去迭代求解鱼卵运动方程的过程，以大幅提高鱼卵速度和运动轨迹的计算效率。

参 考 文 献：

［1］易伯鲁，余志堂，梁秩燊，等.长江干流草，青，鲢，鳙四大家鱼产卵场的分布，规模和自然条件［C］//葛洲坝水利枢纽与长江四大家鱼.武汉：湖北科学技术出版社，1988.

［2］姜伟，刘焕章，段中华，等.以标志物对长江上游漂流性鱼卵漂流方式的研究［J］.水生生物学报，2010，34（6）：1172-1178.

［3］长江四大家鱼产卵场调查队.葛洲坝水利枢纽工程截流后长江四大家鱼产卵场调查［J］.水产学报，1982，6（4）：287-305.

［4］林俊强，彭期冬，黄真理.河流鱼类鱼卵运动的水力学研究进展［J］.水利学报，2015，46（7）：869-876.

［5］唐明英，黄德林，黄立章，等.草、青、鲢、鳙鱼卵水力学特性试验及其在三峡库区孵化条件初步预测［J］.水利渔业，1989（4）：26-30.

［6］罗佳，石小涛，刘德富，等.两种鲟鱼卵在均匀流场中的漂移特性研究［J］.水生生物学报，2013，37（5）：978-981.

［7］GARCIA T，ZAMALLOA C Z，JACKSON P R，et al.A laboratory investigation of the suspension，transport，and settling of silver carp eggs using synthetic surrogates［J］.Plos One，2015，10（12）：e0145775.

［8］王殿常，禹明忠，王兴奎.明槽水流中颗粒运动特性的试验研究［J］.应用基础与工程科学学报，2000，8（3）：301-309.

［9］王烜，张永泽，李嘉.数字图像处理技术在固-液两相流实验中的应用［J］.水动力学研究与进展，1999，14（2）：210-218.

［10］许琳娟，刘春晶，曹文洪.非均匀推移质瞬时输沙率试验研究［J］.水利学报，2016，47（2）：236-244.

［11］PATALANO A，WERNHER B.PTVlab［EB/OL］.［2013-04-11］.http：//cn.mathworks.com/matlabcentral/fileex⁃change/41235-ptvlab--particle-tracking-velovimetry-lab-?requestedDomain=true”.

［12］张扬宗，谭玉钧，欧阳海.中国池塘养鱼学［M］.北京：科学出版社，1989.

［13］MORSI S A，ALEXANDER A J.An investigation of particle trajectories in two-phase flow systems［J］.Journal of Fluid Mechanics，1972，55（2）：193-208.

［14］胡春宏，惠遇甲.水流中跃移颗粒的受力分析［J］.水利学报，1993（1）：11-20.

［15］李嘉，张永泽，李克隆.剪切紊流中颗粒运动的数学模型和实验研究［J］.水利学报，1998（6）：7-14.

［16］刘鉴毅，危起伟，陈细华，等.葛洲坝下中华鲟繁殖生物学特性及其人工繁殖效果［J］.应用生态学报，2007，18（6）：1397-1402.

［17］王悦，杨宇，高勇，等.葛洲坝下中华鲟产卵场卵苗输移过程的数值模拟［J］.水生态学杂志，2012，33（1）：1-4.