考虑材料层次尺寸效应影响的混凝土力学性能理论预测方法

李 冬，金 浏，杜修力，刘晶波

（1.清华大学 土木系，北京 100084；2.北京工业大学 城市减灾与防灾防护教育部重点实验室，北京 100124）

1 研究背景

裂缝问题是我国重大水工混凝土结构工程中的关键问题之一。深入研究大坝混凝土的断裂特性，优化全级配水工混凝土结构设计方法，具有重要的工程和科学意义。混凝土断裂模型中的多种力学参数都存在尺寸效应［1］。尺寸效应，是指以名义强度为代表的力学性能指标随材料或构件尺寸的变化而发生变化，这是准脆性材料的固有特性［2］。基于不同的理论框架，目前主要存在三类混凝土尺寸效应理论：（1）基于“最弱链”理论的统计尺寸效应律［3］；（2）基于断裂力学理论的断裂尺寸效应律［4-7］；（3）基于裂纹分形特性理论的分形尺寸效应律［8］。其中，基于断裂力学基本理论框架的尺寸效应律受到了各国学者较为广泛的关注，典型的如Bažant尺寸效应律（SEL）［4］、Hu-Duan边界效应模型（BEM）［5-6］，以及近年来 Hoover和Bažant［7］提出的对试件几何形状没有限制的通用尺寸效应律（USEL）等。这些尺寸效应理论大多是从宏观尺度出发，根据混凝土材料断裂破坏行为的基本特征，给出其尺寸效应行为的力学描述［9］。资料显示，这些尺寸效应理论在一定尺度范围内均能够较好地描述混凝土的尺寸效应行为，但对于试验数据较为薄弱的大尺寸范围，不同理论给出的变化趋势却不尽相同。这无疑对大型混凝土工程结构（尤其是水工混凝土结构）的安全设计带来了隐患，如何准确预测大尺度混凝土构件的宏观力学性能成为亟待解决的科学问题及难题。

目前，对于混凝土结构尺寸效应问题的研究主要集中于两个层次，即：材料层次和构件层次。混凝土材料层次的尺寸效应是一个复杂的材料科学问题，主要受到骨料粒径、骨料分布、砂浆性能以及初始缺陷等因素的影响［9-11］；混凝土构件层次的尺寸效应则是一个结构力学问题，主要受到混凝土材料本身的非均质性以及钢筋/混凝土相互作用的高度复杂性这两方面的影响［9-11］。由此可见，混凝土宏观力学性能从根本上取决于其材料本身的力学特性，混凝土构件层次尺寸效应理论须建立在材料层次尺寸效应理论基础之上。

骨料在大坝混凝土中用量比例高（约占混凝土材料总质量的90%），最大粒径大（可达150 mm），其材料特性对大坝混凝土性能的影响尤其显著，甚至起着决定性作用［12］。杜修力等［13］研究了骨料空间分布对混凝土压缩强度的影响，结果表明不同骨料分布形式下混凝土压缩强度服从双参数Weibull分布。韩宇栋等［14-15］则研究了粗骨料含量对混凝土力学参数的影响，结果表明粗骨料含量在低强和高强混凝土中对其力学性质的影响规律不同。周尚志等［16］分析了骨料对混凝土断裂行为的影响，结果表明骨料能够增强混凝土的受力和变形特性，并且对混凝土中裂纹的扩展有阻碍作用，骨料粒径越大该作用越明显。Stroeven［17］利用体视学方法，基于几何概率理论，对二维和三维情况下不同级配混凝土的（发展完全的）裂缝尺度（即形态学特征）给出了明确的定量统计公式，但未能与混凝土宏观力学性能建立联系。阮征等［18］分析了骨料和砂浆等影响混凝土强度的细观机理，结果表明骨料的加入会降低水泥基材料的强度，因此混凝土材料的强度小于相同配比条件下的砂浆。李宗利等［19］则给出了能够考虑骨料级配的混凝土有效弹性模量的预测模型，结果表明骨料级配、骨料间相互作用对混凝土弹性模量有较大影响，且骨料体积分数越大，其影响越显著。苏婕等［20］讨论了不同骨料组分（级配）对混凝土立方体抗压强度尺寸效应的影响，结果表明在3种不同骨料组分试件中，混凝土（级配最高、材料均匀性较差）的尺寸效应最为显著，水泥净浆（级配最低、材料均匀性较好）的尺寸效应最为微弱，并且在粗细两种骨料中，尺寸效应对粗骨料组分（粒径较大）反应较为敏感。根据我国《水工混凝土配合比设计规程DLT5330-2015》［21］，水工大体积混凝土宜使用最大粒径较大的骨料。对于不同级配混凝土，由于采用的最大骨料粒径（粗骨料粒径范围为5～150 mm）不同，导致混凝土材料的宏观力学性能易随骨料级配发生变化［22］，即产生材料层次尺寸效应。总体来说，随着骨料粒径的增加，混凝土宏观力学性能有劣化的趋势［23-24］，对于最大骨料粒径在120～180 mm范围的混凝土材料，其抗拉强度相对最大骨料粒径为20 mm的混凝土下降约30%～50%［25］；当最大骨料粒径从10 mm增大至64 mm过程中，混凝土抗压强度减小约10%［26］。此外，由于混凝土断裂参数均与最大骨料粒径有关，通过试验方法测得小尺寸试件的断裂参数能否用于大体积混凝土的设计中仍值得商榷［27］。管俊峰等［28］研究了全级配水工混凝土双K断裂参数的最小试件尺寸，表明若得到不随试件尺寸变化的全级配水工混凝土双K断裂参数，浇注试件的最小尺寸须满足韧带高度与骨料最大粒径比值大于等于6。文献［29-31］则设计了一组简单混凝土断裂模型，通过细观试验方法研究了骨料粒径对混凝土断裂力学参数的影响。总体来说，骨料级配与最大骨料粒径是决定骨料总表面积的主要因素，而骨料总表面积又在很大程度上影响着包裹在骨料外面界面层的体积分数大小，界面层是存在于混凝土细观结构中的薄弱部分，其力学特性亦是影响混凝土断裂破坏行为及其宏观力学性能不可忽略的因素［32］。

本文将从细观角度出发，将混凝土看作由粗骨料颗粒、砂浆基质以及界面过渡区组成的三相复合材料，基于断裂力学基本理论框架，提出一种能够考虑材料尺寸效应影响的预测混凝土宏观力学性能的理论分析方法。

2 单轴拉伸条件下混凝土细观裂缝长度

2.1 混凝土细观断裂模型及其基本假定 在本文作者前期工作［33］中，从细观角度出发，给出了单轴拉伸条件下混凝土细观裂缝长度（lmeso）的理论推导过程，并初步探讨了骨料级配（n）对混凝土单轴抗拉强度（ft）的影响。本文在之前工作的基础上，对该理论模型进行细化并进一步扩展，使之能够充分考虑混凝土细观结构的影响，并对混凝土的强度特性和断裂特性进行描述。

图1给出了用于描述混凝土在细观层次裂缝扩展路径的形态学分析模型，图中，ft、εu分别为混凝土抗拉强度和极限应变；σmo、σITZ和εu，mo、εu，ITZ分别为砂浆基质、界面过渡区的极限应力和极限应变；l为宏观裂缝长度（单轴拉伸条件下即为试件边长）；lITZ、lmo分别为界面裂缝长度和砂浆裂缝长度；ri为粗骨料粒径；θ为界面裂缝对应的圆心角；lITZ*为界面裂缝圆弧对应的弦长。

图1 混凝土细观裂缝扩展路径的形态学分析模型

为便于理论计算，该模型建立在以下3个基本假定上：（1）根据我国《水工混凝土配合比设计规程DLT5330-2015》［21］的相关规定，粗骨料按粒径依次分为小石（5～ 20 mm）、中石（20～ 40 mm）、大石（40～80 mm）和特大石（80～150 mm）4个粒级。根据采用的骨料最大粒径不同，分为一级配（n=1）、二级配（n=2）、三级配（n=3）、四级配（n=4），水工大体积混凝土宜使用最大粒径较大的骨料。小石等效粒径为12 mm、中石等效粒径为30 mm、大石等效粒径为60mm、特大石等效粒径为120 mm，其针对不同级配情况下的组合比（an）依据文献［21］中表5.3.1的相关规定。本文假定骨料为圆形或球形，且不发生破坏，因此采用卵石级配。（2）细骨料（粒径小于5mm的骨料）与水泥砂浆共同组成砂浆基质，力学性能可通过试验方法确定。（3）将界面过渡区看作含初始缺陷（如裂隙、孔洞等）较多的砂浆基质，其力学性能相对于砂浆基质较弱。

2.2 混凝土细观裂缝长度计算方法 混凝土单轴受拉断裂裂缝在细观尺度上的总长度lmeso由砂浆基质在垂直主拉应力方向上的断裂裂缝总长度lmo与界面过渡区中的断裂裂缝总长度lITZ两部分组成［33］。定义一个混凝土细观裂缝曲折度指数λ，令：

式中：l为宏观裂缝长度（单轴拉伸条件下即为试件边长）；lITZ、lmo分别为界面过渡区和砂浆基质中的裂缝总长度，根据文献［33］的推导，有：

故：

式中：α、β分别为界面过渡区和砂浆基质中的裂缝长度分配系数，η为界面裂缝指数，其用于确定界面过渡区中裂缝的长度，当η=0时，界面裂缝长度lITZ=0；当η=0.5时，θ=180°，界面裂缝长度lITZ=πri；γ为粗骨料含量，实际混凝土中骨料（含细骨料和粗骨料）含量约在60%～70%之间，其中粗骨料含量约为45%，因此取γ≤0.45；n、an分别为粗骨料级配和相应级配骨料含量的组合比［21］，如表1所示。

图2给出了细观裂缝曲折度指数λ随细观材料参数（n、η、γ）的变化趋势。从图2可以看到，随着粗骨料级配n、界面裂缝指数η以及粗骨料体积分数γ的提高，细观裂缝曲折度指数亦提高，相应的混凝土细观裂缝长度增大。从图2（a）（b）可见，对于粗骨料体积分数为45%（γ=0.45）的混凝土试件，当界面裂缝指数η=0时，即界面裂缝长度lITZ=0，此时混凝土细观裂缝仅在砂浆中扩展。因此，基于本文模型的基本假定，其细观裂缝曲折度指数λ=0，即混凝土细观裂缝长度lmeso=l；随着界面裂缝指数的提高，混凝土细观裂缝的曲折程度亦提高，并且随着骨料级配的增加，其提高程度亦逐渐增加。从图2（c）可以发现，假定界面裂缝指数η=0.4，随着粗骨料体积分数的增加，混凝土细观裂缝的曲折程度亦提高，并且随着粗骨料级配的增加，其提高程度亦逐渐增加。

表1 不同粗骨料级配混凝土配合比［33］

图2 细观裂缝曲折度指数λ随细观材料参数（n、η、γ）的变化趋势

3 混凝土材料特性

3.1 断裂能基本原理 根据Bažant等［2］的研究，对于一受单轴拉伸的混凝土试件，其受拉裂缝扩展单位长度δl扫过的面积为δA=bδl（对于二维混凝土试件b=1），则该单位面积开裂所需要的总功为：

式中，Gf为混凝土断裂能。

假设结构吸收的总外力功为W，则任意瞬时总外力功的增量为δW，其中，一部分能量储存为弹性应变能（δU），一部分用于使混凝土开裂（δWR），其他能量则用于使其产生动力效应（δK）。因此，可以得到：

对于静力问题，δK=0，根据能量守恒原理，可以得到：

式中，Gr为能量释放率。

即当用于裂缝扩展的能量（δWR）等于裂缝扩展需要的能量（δWF）时，裂缝即扩展。这也是经典的线弹性断裂力学理论的基本原理。

实际上，式（7）更一般的表达式是［2］：

基于式（8），可以提出三种断裂准则，即：

3.2 力学参数推导 本文模型中，为便于推导计算，假设结构吸收的外力功最终均用于裂缝的扩展（δU=0），并且材料断裂过程是准静态的（δK=0），根据式（10）可以得到：

这里，混凝土断裂能Gf是一个宏观平均的断裂参数，而能量释放率Gr则需要由混凝土材料内部各细观组分的断裂特性决定。根据文献［29-31］基于简单混凝土断裂模型的细观试验，任意材料的断裂能可以表达为：

因此，在宏观层次上，混凝土断裂能可以表达为：

其中：ω为混凝土的应变能密度，即应力应变曲线下面积，如图1（a）所示；ft为混凝土抗拉强度；εu为混凝土极限应变。

在细观层次上，砂浆基质和界面过渡区的断裂能可以分别表达为：

式中：ωmo、ωITZ分别为砂浆基质和界面过渡区的应变能密度，σmo、σITZ和εu，mo、εu，ITZ分别为砂浆基质和界面过渡区的极限应力和极限应变。

文献［29-31］的工作，本文认为宏观层次混凝土能量释放率是由细观层次砂浆基质和界面过渡区这两方面的贡献共同组成的，则：

结合式（2）、式（3）、式（12）、式（14）、式（15）和式（16），可以得到细观层次上混凝土的断裂能为：

其中，ω*=αωITZ+(1-β)ωmo为细观层次混凝土应变能密度。

基于以上推导，可以得到混凝土抗拉强度、特征长度及脆性指数［34-35］分别为：

3.3 参数分析及讨论 式（18）—式（21）即为基于本文建立的混凝土细观断裂模型推导得到的混凝土宏观力学性能的理论预测方法。其中，试件尺寸l、粗骨料含量γ、粗骨料级配n以及相应级配骨料含量的组合比an均是实际可测的或为已知参数，而界面裂缝指数η为未知参数。根据文献［33］中的推导，由裂缝扩展遵循“最低能量原理”［36］，可以得到：

由式（22）可以发现，界面裂缝指数仅取决于界面过渡区和砂浆基质二者力学性能的比值。文献［29-31］在其细观试验中指出，对于骨料强度较高的混凝土材料（即裂缝无法贯穿骨料颗粒），由于其细观断裂裂缝或在砂浆基质中扩展或在界面过渡区中扩展，因此该混凝土材料的宏观断裂能应等于或小于砂浆基质的断裂能。式（22）恰好反映了文献［29-31］的试验现象及结论：（1）当界面过渡区的力学性能较强时，极限状态为与砂浆基质的力学性能完全相同，即ωITZ=ωmo，则有η=0，细观断裂裂缝均在砂浆基质中扩展，根据式（18），可以得到Gf=ωmol，此时混凝土材料的宏观断裂能与砂浆基质的断裂能相等（上限）。（2）当界面过渡区的力学性能较弱时，极限状态为粗骨料与砂浆基质之间的界面层在混凝土试件受力之前已完全分离，即ωITZ=0，则有η=0.5，细观断裂裂缝极大部分在界面过渡区中扩展，根据式（18），可以得到Gf=（1-β）ωmol，此为混凝土材料的宏观断裂能的下限。

此外，需要说明的是，式（19）—式（21）中混凝土极限应变εu和弹性模量E并未给出具体表达式。对于混凝土极限应变εu，基于本文建立的混凝土细观断裂模型及其基本假定，从混凝土材料细观断裂过程角度分析，这里认为εu=εu，mo［33］。对于混凝土弹性模量E，文献［29-31］的细观试验研究表明，混凝土弹性模量小于或等于砂浆基质的弹性模量值，并且当界面过渡区性能较弱时，骨料粒径不影响混凝土弹性模量，因此本文假设E≤Emo。

4 方法验证及扩展分析

4.1 方法验证 文献［29-31］设计了一组简单的混凝土细观断裂模型，用于研究混凝土材料断裂裂缝扩展路径及骨料尺寸对其断裂能等力学参数的影响。表2中列出了该模型中采用的各细观组分的力学参数。该模型主要特点：水泥和细砂共同组成砂浆基质；骨料体积分数为25.8%，采用两类平均粒径为7.4 mm的球状莫来石（Mullite）作为骨料颗粒，强骨料抗拉强度平均约16 MPa，弱骨料抗拉强度平均约1.7 MPa；界面过渡区则设置为3种不同的力学性能，强界面的断裂能为50±10 J/m2，中强界面的断裂能为30±10 J/m2，弱界面的断裂能为10±10 J/m2。

根据本文建立的混凝土细观断裂模型及其基本假定，采用表2中砂浆基质、强骨料和不同性能界面过渡区组合的试验结果进行验证，即：l=40mm、γ=0.258、n=1、r=3.7 mm、Gf，mo=52 J/m2、Gf，ITZ-1=50 J/m2、Gf，ITZ-2=30 J/m2、Gf，ITZ-3=10 J/m2。根据式（22）可以得到，3种力学性能界面过渡区对应的界面裂缝指数分别为：η1=0.088、η2=0.304和η3=0.439。基于建立的混凝土材料特性求解方法，根据式（1）—式（4）和式（18）—式（21）可以得到如表3所示的各项宏观力学性能的理论计算值。

从表3中可以发现，随着裂缝界面指数η的增大（即随着界面力学性能的减弱），混凝土细观裂缝曲折度指数λ亦增大，相应的细观裂缝长度lmeso也增加，而混凝土宏观断裂能Gf随界面力学性能的减弱而逐渐减小。

表2 细观断裂模型中各细观组分的力学参数

表3 各项宏观力学性能的理论计算值

图3给出了文献［29-31］试验测得的混凝土断裂能（Gf）随界面过渡区力学性能（裂缝界面指数η）变化趋势与基于本文方法的理论预测值的对比，试验结果与理论结果趋势基本一致，表明本文理论方法是合理的。

文献［29-31］在其细观试验中亦指出，对于具有相同骨料体积含量的混凝土材料，提高其断裂能的最佳方式即是提高界面过渡区的力学性能。此外，从表3中还可以发现，随着界面过渡区力学性能的减弱，混凝土抗拉强度ft随之减小，而特征长度lch则增加，相应的脆性指数B下降，这均与混凝土材料的非均质性相关，即界面层的强弱能够显著影响混凝土材料的均匀性。

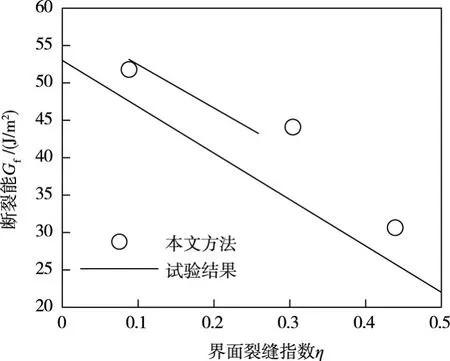
图3 本文方法与试验结果对比

4.2 扩展分析 由以上分析可知，混凝土材料层次尺寸效应实际上是其宏观力学性能随骨料、砂浆、界面等细观组成材料参数尺度的变化。此外，根据我国《水工混凝土配合比设计规程DLT5330-2015》［21］，水工大体积混凝土宜使用最大粒径较大的骨料。因此，本文令l=450 mm、γ=0.45，n=1、2、3或4，即对粗骨料含量约45%的不同级配大坝混凝土标准立方体试件的材料层次尺寸效应行为进行分析。假设界面过渡区力学性能为砂浆基质力学性能的80%（η=0.279）或60%（η=0.383），根据式（18）—式（21）可以得到，大坝混凝土的断裂能、抗拉强度、特征长度以及脆性指数随粗骨料级配的变化曲线，如图4所示。从图4可以发现，混凝土断裂能和抗拉强度均随粗骨料级配的增大而呈现减小的趋势，而其特征长度随粗骨料级配的增大亦增大，脆性指数则呈现与特征长度相反的趋势。这显然是受到了骨料尺寸的影响，即随着骨料级配的增大，最大骨料粒径随之增大，使得混凝土材料的均匀性降低，必然导致其特征长度变大，脆性指数减小，并且受到非均质性的影响，混凝土断裂能和抗拉强度减小。此外，对比不同界面力学性能（η=0.279或η=0.383）对混凝土宏观力学性能的影响可以发现，当界面力学性能较弱时，混凝土材料特性随粗骨料级配的变化趋势更加明显，即随着界面力学性能的降低，混凝土材料层次尺寸效应行为更加显著。

图4 混凝土力学参数随粗骨料级配变化

此外，粗骨料体积含量也是影响混凝土材料宏观力学性能的重要因素，因此令l=450 mm、η=0.383，γ=0.15、0.25、0.35或0.45，对不同级配大坝混凝土标准立方体试件的材料层次尺寸效应行为进行分析。根据式（18）—式（21）可以得到，混凝土宏观力学参数随粗骨料含量的变化曲线，如图5所示。从图5可以看到，混凝土断裂能、抗拉强度以及脆性指数均随粗骨料体积分数的增加而逐渐减小，这是由于骨料的加入降低了混凝土材料的均匀性，混凝土特征长度随粗骨料体积分数的增加而增加，亦表明随着粗骨料含量的增大混凝土材料的非均匀性亦增大，并且随着骨料级配的增大，其非均匀程度更加显著。

图5 混凝土力学参数随粗骨料含量变化

5 结论和讨论

本文基于细观力学分析方法，认为混凝土是由粗骨料颗粒、砂浆基质以及界面过渡区组成的三相复合材料，假定骨料颗粒在混凝土受力过程中不发生破坏，采用双线性本构模型描述砂浆基质和界面过渡区的材料力学行为。基于断裂力学基本理论框架，推导得到了混凝土细观裂缝长度、宏观断裂能、单轴拉伸强度、特征长度以及脆性指数等力学参数的理论预测公式。通过与试验数据的对比，验证了建立的细观断裂模型和理论分析方法的合理性。最后，基于本文提出的理论预测方法，分析了界面过渡区力学性能以及粗骨料级配和含量对混凝土宏观力学性能的影响，主要得到如下几点结论：（1）粗骨料粒径（级配）和含量对混凝土材料的宏观力学性能有显著影响，即存在材料层次的尺寸效应行为，如断裂能和抗拉强度均随粗骨料级配和含量的增大而减小，特征尺寸则随粗骨料级配和含量的增大而增大，相应的脆性指数呈现与特征长度相反的趋势。（2）界面过渡区的力学性能亦能够显著影响混凝土材料的宏观力学性能，随界面力学性能的降低，混凝土材料层次的尺寸效应行为更加显著。（3）增大粗骨料粒径/含量和减弱界面过渡区的力学性能均能够显著影响混凝土材料的均匀性，故而产生混凝土宏观力学性能随细观组分力学性能的变化而变化的行为，即混凝土材料的非均质性是产生材料层次尺寸效应的根源。

本文初步建立的用于混凝土材料宏观力学性能研究的细观断裂模型及理论分析方法仅适用于普通混凝土在准静力加载条件下破坏行为的研究。针对高强混凝土或高应变率加载条件下混凝土的断裂失效行为，由于存在骨料破裂等现象，因此需要在本文研究基础上进行修正或扩展，后续将就这一问题进行深入探讨。此外，大坝混凝土宏观力学性能除了与其配合比、骨料级配有关外，还与骨料形状、骨料本身的性质（如骨料岩体的组成及成分）等有关。实际上粗骨料的形貌学特征包括颗粒粒形、尺寸、棱角性和表面纹理，是影响新拌混凝土流动性和硬化混凝土密实度、强度和体积稳定性的重要因素［37-38］。本文主要是基于圆形骨料情况进行的，针对真实骨料的多边形特性等，后续将基于本文模型中的圆形骨料，对其形状进行修正，从细观裂缝长度方面入手，考虑骨料形状等因素对混凝土宏观力学性能的影响。

随机性也是影响混凝土宏观力学性能不确定性的重要因素，如施工方法和温控措施等施工因素的影响。此外，混凝土属于非均质材料，在外荷载作用下，骨料周围有应力集中存在，裂缝多起源于骨料与砂浆之间的界面，但究竟始于骨料表面哪个部位，朝哪个方向发展则主要取决于外力方向等因素。本文为便于理论推导并给出具有实际物理意义的模型参数，建立的理论分析模型实际上是对混凝土材料的真实断裂状态进行了一定的简化，这一处理方式可以使各类随机影响因素得到定量表达，也因此使得本文模型分析方法成为确定性方法。文中提出的界面裂缝指数虽能够初步考虑骨料特性的随机性等导致的界面强度变化方面的影响，但对于混凝土材料性能以及破坏模式等的随机性特征目前未能充分体现在本文模型中。在后续工作中，将在本文理论分析模型合理的基础上进一步完善，充分考虑其他影响因素造成的混凝土宏观力学性能的随机性行为。

参 考 文 献：

［1］刘兴阳，邹德高，李占超.混凝土名义强度的尺寸效应研究［J］.建筑材料学报，2017，20（5）：680-684.

［2］BAŽANT Z P，PLANAS J.Fracture and size effect in concrete and other quasibrittle materials［M］.CRC Press，1997.

［3］WEIBULL W.A statistical distribution function of wide applicability［J］.ASME Journal of Applied Mechanics，1951，181（2）：293-297.

［4］BAŽANT Z P.Size effect in blunt fracture：concrete，rock，metal［J］.Journal of Engineering Mechanics，1984，110（4）：518-535.

［5］DUAN K，HU X，WITTMANN F H.Scaling of quasi-brittle fracture：Boundary and size effect［J］.Mechanics of Materials，2006，38（1/2）：128-141.

［6］管俊峰，胡晓智，王玉锁，等.用边界效应理论考虑断裂韧性和拉伸强度对破坏的影响［J］.水利学报，2016，47（10）：1298-1306.

［7］HOOVER C G，BAŽANT Z P.Universal size-shape effect law based on comprehensive concrete fracture tests［J］.Journal of Engineering Mechanics，2014，140（3）：473-479.

［8］CARPINTERI A，FERRO G A.Size effects on tensile fracture properties：a unified explanation based on disorder and fractality of concrete microstructure［J］.Materials and Structures，1994，27（10）：563-571.

［9］杜修力，金浏，李冬.混凝土与混凝土结构尺寸效应述评（Ⅰ）：材料层次［J］.土木工程学报，2017，50（9）：28-45.

［10］杜修力，金浏，李冬.混凝土与混凝土结构尺寸效应述评（Ⅱ）：构件层次［J］.土木工程学报，2017，50（11）：24-44.

［11］BAŽANT Z P，KWON Y W.Failure of slender and stocky reinforced concrete columns：tests of size effect［J］.Materials and Structures，1994，27（2）：79-90.

［12］石妍，杨华全，陈霞，等.骨料种类对混凝土孔结构及微观界面的影响［J］.建筑材料学报，2015，18（1）：133-138.

［13］杜修力，韩亚强，金浏，等.骨料空间分布对混凝土压缩强度及软化曲线影响统计分析［J］.水利学报，2015，46（6）：631-639.

［14］韩宇栋，张君，高原.粗骨料体积含量对混凝土断裂参数的影响［J］.工程力学，2013，30（3）：191-197.

［15］韩宇栋，张君，王振波.粗骨料体积分数对混凝土弹模和抗压强度的影响［J］.哈尔滨工业大学学报，2013，45（4）：84-91.

［16］周尚志，谌林，刘明群.骨料对混凝土力学性能的影响分析［J］.建筑材料学报，2016，19（1）：143-148.

［17］ STROEVEN P.Stereological approach to roughness of fracture surfaces and tortuosity of transport paths in con⁃crete［J］.Cement and Concrete Composites，2000，22（5）：331-341.

［18］阮征，陈力，洪建，等.骨料和砂浆等影响混凝土强度的细观层次机理分析［J］.建筑材料学报，2014，17（6）：952-958.

［19］李宗利，邓朝莉，张国辉.考虑骨料级配的混凝土有效弹性模量预测模型［J］.水利学报，2016，47（4）：575-581.

［20］苏捷，方志.不同骨料组分混凝土立方体抗压强度尺寸效应试验研究［J］.建筑结构学报，2014，35（2）：152-157.

［21］DL/T 5330-2015，水工混凝土配合比设计规程［S］.北京：中国电力出版社，2015.

［22］石建光，许岳周，叶志明.骨料级配对混凝土性能影响的细观分析［J］.工程力学，2009，26（4）：134-138.

［23］杜敏，金浏，李冬，等.粗骨料粒径对混凝土弯拉强度尺寸效应影响的试验研究［J］.北京工业大学学报，2016，42（6）：912-918.

［24］杜敏，金浏，李冬，等.骨料粒径对混凝土劈拉性能及尺寸效应影响的细观数值研究［J］.工程力学，2017，34（9）：54-63.

［25］THOMAS T C，SLATE F O.Tensile bond strength between aggregate and cement paste or mortar［J］.ACI Jour⁃nal Proceedings，1963，60（4）：465-486.

［26］HUGHES B P，CHAPMAN G P.The deformation of concrete and micro-concrete in compression and tension with particular reference to aggregate size［J］.Magazine Concrete Research，1966，18（54）：19-24.

［27］PETERSSON P E.Fracture energy of concrete：Practical performance and experimental results［J］.Cement&Concrete Research，1980，10（1）：91-101.

［28］管俊峰，李庆斌，吴智敏，等.确定现场浇筑全级配水工混凝土双K断裂参数的最小试件尺寸［J］.应用基础与工程科学学报，2016，24（6）：1219-1231.

［29］ROSSELLÓ C，ELICES M.Fracture of model concrete：1.Types of fracture and crack path［J］.Cement and Con⁃crete Research，2004，34（8）：1441-1450.

［30］ROSSELLÓ C，ELICES M，GUINEA G V.Fracture of model concrete：2.Fracture energy and characteristic length［J］.Cement and Concrete Research，2006，36（7）：1345-1353.

［31］ELICES M，ROCCO C G.Effect of aggregate size on the fracture and mechanical properties of a simple concrete［J］.Engineering Fracture Mechanics，2008，75（13）：3839-3851.

［32］董芸，杨华全，张亮，等.骨料界面特性对混凝土力学性能的影响［J］.建筑材料学报，2014，17（4）：598-605.

［33］李冬，金浏，杜修力，等.骨料级配对二维模型混凝土单轴抗拉强度影响的理论研究［J］.工程力学，2017，34（6）：64-72.

［34］HILLERBORG A，MODÉER M，PETERSSON P E.Analysis of crack formation and crack growth in concrete by means of fracture mechanics and finite elements［J］.Cement&Concrete Research，1976，6（6）：773-781.

［35］HILLERBORG A.Results of three comparative test series for determining the fracture energy GF of concrete［J］.Materials and Structures，1985，18（5）：407-413.

［36］STROEVEN P.Some observations on microcracking in concrete subjected to various loading regimes［J］.Engi⁃neering Fracture Mechanics，1990，35（4）：775-782.

［37］李北星，王威，陈梦义，等.粗骨料的等轴率、圆度和球度及其相互关系［J］.建筑材料学报，2015，18（4）：531-536.

［38］杜成斌，孙立国.任意形状混凝土骨料的数值模拟及其应用［J］.水利学报，2006，37（6）：662-667.