大面阵航摄影像重建高效像素插值算法研究
胡海彦,余旭初,杨韫澜,方 勇,江振治
(1.信息工程大学,河南 郑州 450001;2.西安测绘研究所,陕西 西安 710054)
复合型大面阵或超大面阵航摄相机提供给作业用户的最终影像,其每一个像素都是从原始子影像重采样而来,就计算耗时而言,根据经验图像重采样所耗费的时间至少要占到整个大面阵航摄影像预处理的1/3以上,所以对此环节进行耗时优化,必然会极大提升大幅面影像生成效率[1-3]。图像内插重建是基于一组等间距离散采样点恢复连续空间图像函数的过程,其是图像缩放、子像素平移(非整像素)、图像旋转、图像形变等基本图像操作的技术基础。当这些图像操作所在位置缺少既有图像灰度值,即需要图像插值进行灰度填补。而且对于大幅面数字航摄相机而言,在影像复合过程中可通过高精度像素重采样一并解决镜头畸变引起的图像几何失真、色彩配准等图像重建问题。由采样理论可知,sinc函数是最为理想的图像插值内核函数(见图1)。然而,实际应用中并不能直接使用该函数进行插值[4],需要有限截断并实现离散化计算,同时要在计算速度与数学精度之间取得平衡,即在尽可能接近sinc函数理论精度的前提下,设计出一个内核函数对sinc进行函数逼近。通常可以通过n阶对称分段多项式进行内核函数逼近,如常用的双线性卷积核函数等即为其中一种特例,文献[5]对此类内核函数进行了定量评估,相关研究也比较丰富[6~9],但往往给出的插值算法精度接近像素级,也没有挖掘此类算法的潜在效率,仅适用于图像融合等某些常规应用。本文从一维信号重构原理着手,推导出n阶对称分段多项式内核函数的数学形式,并给出多项式定义域变换后的加速算法实现,最后对所提算法实作性能进行试验分析。算法在尽可能不引入额外像素插值误差,从而避免损失或破坏影像自身固有几何量测精度前提下,大幅度降低数据处理计算复杂度,满足大幅面数字航摄影像重建对效率的要求。

图1 空间域中的sinc函数
1 像素插值算法
1.1 内核函数的多项式逼近
对于一维空间,近似sinc内核函数的n阶对称分段多项式在区间[-(n-1),(n-1)]上的定义为
(1)
其中:i=0,1,…,m-1,m表示整数截断范围,满足n=2m-1。这样总共会有(n+1)m个aij系数。由于内核函数具有对称性及维度的可分离性,即二维内核函数为两个一维内核函数的乘积,即h(x,y)=h(x)h(y),所以为了描述的简洁性,本文均在一维情况下予以讨论。
为了保证节点处函数拟合的连续性与光滑性,除保证多项式与sinc函数在节点上的取值相同外,还需要对式(1)附加导数连续性约束条件。以下将3阶对称分段多项式内核函数作为样例,给出推导过程,更高阶多项式类同。在区间[-2,2]上sinc函数的近似3阶对称多项式内核函数为
hC(x)=
(2)
由约束条件(2)总共可列出7个方程,其中含8个未知数系数。进一步令a13=α作为调整参数,则未知数个数减1,使得方程组可解。有
a03=(α+2),a02=-(α+3),a01=0,a00=1
a13=α,a12=-5α,a11=8α,a10=-4α.

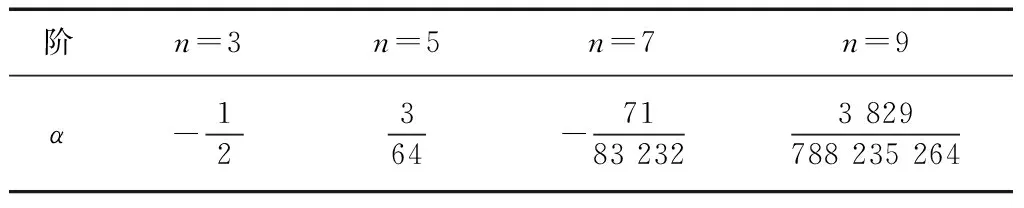
表1 平坦性约束下的3~9阶多项式α参数
可以看出不同的α值,对应不同的插值计算,常用的3次卷积对应α=-1/2,也称之为基斯(Keys)插值内核函数[10](见图2)。
hkeys=
(3)
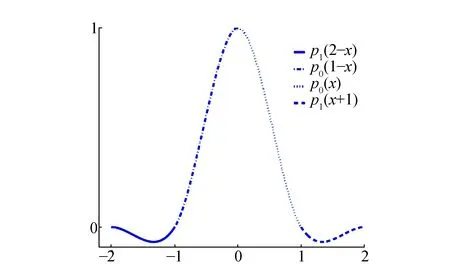
图2 基斯3次卷积内核函数
1.2 多项式定义域转换
内插权重计算即是利用分段多项式求得采样点集上对应的多项式函数值,以此求得卷积核模板,与采样点进行卷积运算便完成插值点函数插值。所以需要先行计算插值点到采样点的相应距离ξ。在3次卷积核的情况下,这些距离值分别为ξ,1-ξ,1+ξ及2-ξ,其中ξ∈[0,1]。考虑计算效率与便捷性,可将所有多项式的定义域区间变换为区间[0,1],利用多项式的分段对称性(图2(a)已给出图示),可对式(1)中的多项式p0(x)在ξ=x,ξ=1-x及p1(x)在ξ=x+1,ξ=2-x上进行分段处理。对于更高的n阶多项式内核函数,实现的策略是相同的,这样可以得到n+1个相同定义域的分段多项式,对于偶数i,即(0,2,4,6…)。令k=i/2,即(0,1,2,3…)。则有
(4)
其中,
(5)
对图2进行3次多项式定义域变换后对应的函数图形如图3所示。

图3 定义域变换为[0,1]的Keys 3次卷积核
为了节约计算时间,给出关于变换后多项式系数属性的5条规则。图4为图形化说明(以5阶插值内核函数系数表为例,α=3/64;表2为3阶插值内核函数系数,α=-1/2)。
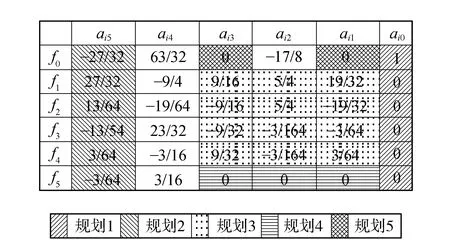
图4 5阶插值多项式内核函数系数图示
规则1:仅第一个多项式f0(x)的最低阶项系数为1,其余多项式fi(x)最低阶项系数ai0均为0;
规则2:多项式fi(x)和fi+1(x),最高阶项系数ain成对相等、符号相反;
规则3:所有j≤-2阶项系数成对出现,且奇数阶项大小相等符号相反、偶数阶项大小相等且符号相同;
规则4:多项式fn(x)的所有j≤n-2阶数项的系数anj为0;
规则5:多项式f0(x)的所有j≤n-2(j为奇数)阶数项的系数a0j为0。
利用这5个规则,可以明显提升计算效率。首先对于所有多项式,距离x具有相同的值,因此可以对x幂进行预先计算。而且成对相同的系数及与x幂相乘的积仅需计算1次,同时可跳过具有零系数的计算项。
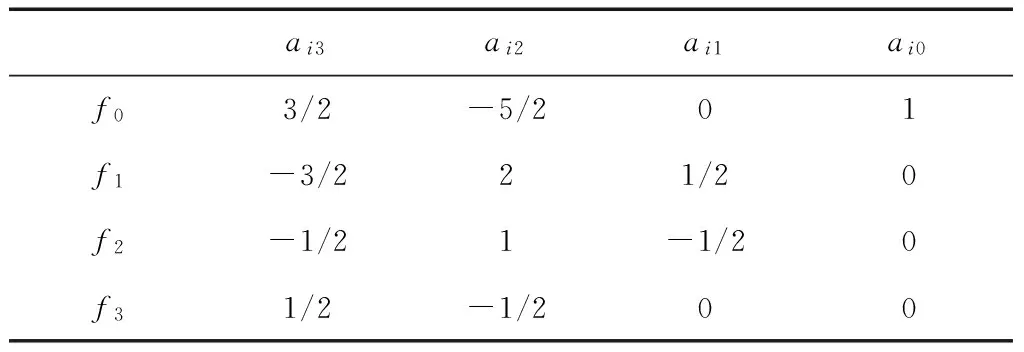
表2 多项式变换后的3次卷积核系数
所以,式(3)给出的Keys 3次卷积核,根据上述理论进行多项式转换,可等价得到[0,1]空间上的4个多项式为
(6)
2 算法性能分析及试验结果
2.1 性能分析
表3给出一维3阶多项式卷积核插值权重的计算次数。对于一维3阶卷积,这里提出的方法总共只需16个计算操作,若替代传统方法的26个计算操作,可使计算加速1.625。表4为n阶多项式卷积核运算次数,随着多项式阶数的增加,加速倍率逐渐降低(例如9阶多项式的加速倍率为1.52),对于无穷阶多项式,加速倍率稳定为4/3。由于分段n阶卷积是可分离的(卷积级联),所以高维N-D卷积的计算耗时是N×1D卷积时间。
当然,要对整个插值操作进行评估时,除需要考虑插值多项式权重计算外,还有采样点与这些权重的卷积计算。该卷积计算的时间复杂度由(n+1)N个加法、乘法和计算机内存访问耗时共同决定。这也意味着当进行高维插值(N>2)时,卷积计算量占主导地位。但通过将多项式定义域变换为[0,1]区间后,对任意维度下的插值都具加速效果,只是此方法对于一、二维低维度插值而言更为高效。

表3 3阶多项式一维卷积核运算次数

表4 n阶多项式卷积核最大运算次数估计
2.2 试验结果
用C++程序语言对上述高阶多项式内核卷积进行算法实现。在配置为Intel Core i3-370M(2.4 GHz)的计算机上完成试验测试。为了进一步加速高阶多项式的计算效率,编程中同时采用查找表(LUT)数据结构对内核函数进行预先计算,为保证插值精度,查找表中将单位长度设置为10 000个网格点(即插值像素点位可精确到0.000 1)。在3阶多项式情况下,由于内存访问相对多项式直接计算耗时,所以采用查找表比直接计算反而略显低效——构建查找表耗时18 982 ms,整个插值过程耗时51 193 ms,但更高阶内核插值试验表明,采用查找表仍是必要的,所以在编码实现时建议分3阶以下/以上多项式两种情况进行程序设计。为了排除计算的偶然性,获取插值时长的平均值,对指定影像总共反复执行100次插值处理,二维插值的试验结果如表5所示。

表5 试验结果 ms
可以看出,新的多项式计算耗时相比常规计算提速比为1.73倍,接近理论值1.625。整个二维3次卷积计算与传统方法相比提速比为1.15倍。这里所用影像数据为西安测绘研究所研制的DMZ大面阵航摄相机实摄航空影像,raw数据为12个子影像,内插合成后的影像像幅为24 K×24 K(见图5)。

图5 DMZ大面阵航摄相机实摄航空影像内插合成
3 结 论
本文提出分段多项式核函数高效插值算法,数学形式简洁统一。相比较于常规插值方法,新的3阶多项式算法耗时提速比为1.625倍,对于任意高阶多项式,耗时提速比上限为1.3倍。这说明新插值算法对常规插值算法具有一定的替代性。
对于大幅面数字航空摄像机而言,因为用于图像重建的插值计算量十分巨大,因此,本文方法对更为快速高效地进行原始摄影数据预处理意义非凡,已对西安测绘研究所研制的国产DMZ大面阵航测相机进行相关试验,由于航测相机要求的量测精度极高(最低子像元级),利用文中的高阶多项式内核函数,可保证所引入的插值误差被忽略不计(实践表明采用5阶多项式已足够有效),这使得大幅面影像生成兼顾效率与精度,进而保障相机的使用效能。还需说明的是,所提方法不限于大幅面数字航空相机的子影像复合拼接应用,需要高精度、高效率的图像插值应用场合,该算法都可发挥一定的作用。当然,可将此算法进一步结合当代GPU并行编程技术予以实现,使得实际作业效率提升更为显著。
参考文献:
[1] 郭海青.信息化航空摄影测量生产与管理系统建设[J].测绘通报,2014(11):53-72.
[2] 刘翠.大面阵CCD成像系统关键技术[J].科学与财富,2015(2):127-128.
[3] 葛明,许永森,沈宏海,等.航空相机大面阵CCD多自由度拼接方法研究[J].红外与激光工程,2015(3):923-928.
[5] MEIJERING E,NIESSEN W,VIERGEVER M.Quantitative evaluationofconvolution-basedmethodsformedicalimageinterpolation[J].Medical Image Analysis,2001,5:111-126.
[6] 钟宝江,陆志芳,季家欢.图像插值技术综述[J].数据采集与处理,2016(6):1083-1096.
[7] 杨文波.航空图像超分辨率重构技术研究[D].长春:中国科学院长春光学精密机械与物理研究所,2014.
[8] 乔少华,李润鑫,刘辉,等.基于统计量的加权函数图像重建方法[J].传感器与微系统,2017(9):53-56.
[9] 赵秀影,王洪玉,从福仲.亚像元几何图像成像与超分辨恢复算法[J].光学技术,2010,36(5):795-798.
[10] KEYS R G.Cubic convolution interpolation for digital image processing[C].IEEE Transactions on Acoustics,Speech,and Signal Processing,1981,29(6):1153-1160.
[11] Weisstein E W.Horner’s rule.Eric Weisstein’s World of Mathematics.2003c,http://mathworld.wolfram.com/HornersRule.html

