江苏地区Tm-Ts相关性分析及其线性模型的建立
朱明晨,胡伍生
(1.东南大学 交通学院,江苏 南京 210096;2.铜陵学院 建筑工程学院,安徽 铜陵 244061)
1 加权平均温度的计算原理及其季节性变化特征
对流层加权平均温度可由测站上空的水汽压(e)和绝对温度(T)沿天顶方向的积分值算得到,其定义如式(1)所示[9]:
(1)
由于大气水汽基本分布在地面上空12 km以内,无线电探空气球可以提供地面至20多km大气的温度、湿度等气象要素的探空轮廓线,因此可以将式(1)简化为式(2)[9]:
(2)
其中Z2和Z1分别为探空数据上下层的高度值。
利用式(2)及所收集的江苏区域5个气象探空站的11年的气象探空数据,计算其加权平均温度,得到该区域的Tm与Ts的变化,如图1所示。

图1 Tm与Ts变化图
由图1可以看出,Tm与Ts随时间变化趋势整体上较为一致,说明在江苏地区适合建立局部的Tm-Ts计算模型。同时无论是Tm还是Ts都具有明显的年周期性,但各城市的周期并不完全同步,且图形的峰顶所对应时段Tm与Ts的变化趋势与谷底处并不十分一致。因此在所有时间段仅使用相同的线性公式,必然会影响Tm的计算精度。
2 江苏地区Tm-Ts线性相关性分析
为分析江苏地区Tm与Ts的线性关系,利用所收集的11年的探空数据分别绘出Tm与Ts之间的散点图如图2所示。
该说认为,农村集体经济组织应属于民事法律关系上“其他组织”范畴。因为如果把农村集体经济组织定位为法人组织,只要该村集体组织一直存在,就不会发生破产情形,这与法人的性质是相违背的。而且一些当代新型的农村经济组织并不一定要有法人身份才可以开展自主活动。很多情况下,农村集体经济组织不一定依法人资格才能成为市场主体,作为非法人组织一样可以释放市场活力,可以享受权利和承担责任。因此,该理论主张其为非法人组织。
由图2可以看出,江苏附近地区的5个城市Tm与Ts之间整体上呈线性变化的规律,将5个城市的数据按照公式Tm=aTs+b分别进行整体的线性回归拟合,得到各个城市的回归系数如表1所示。
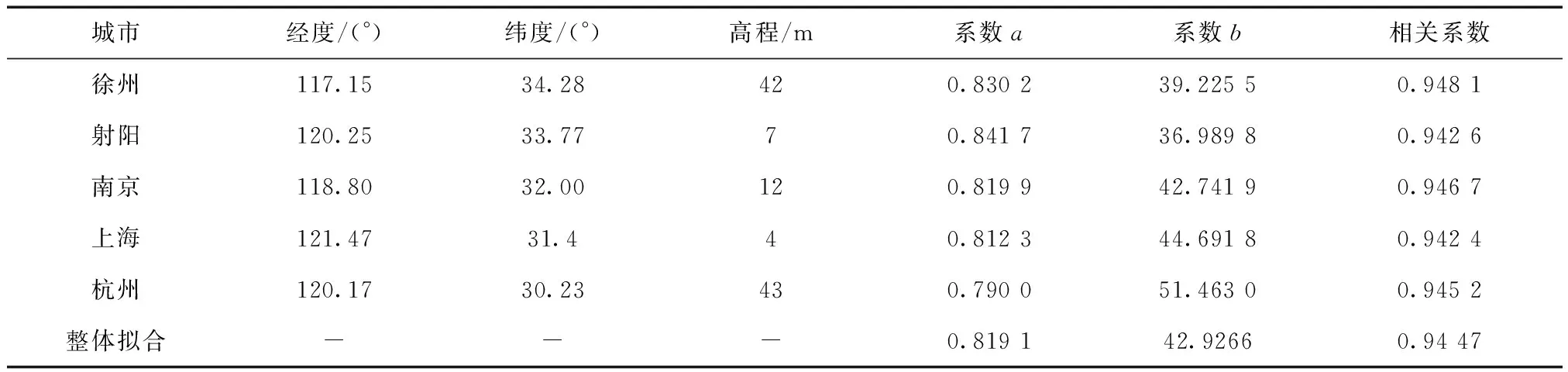
表1 不同城市数据整体线性回归系数表
一般而言,相关系数在0.7~1之间就属于强线性相关[10],江苏附近地区的5个城市的相关系数均大于0.94,且各个城市11年数据整体拟合得到的系数a最大相差不足0.05,因此在试验地区内,可以忽略纬度因素对Tm与Ts相关性的影响,同时由相关系数可以看出,沿海城市的相关系数较之内陆的要小。
为分析江苏附近地区Tm与Ts之间的线性关系随季节的变化,将11年的数据按年积日归类并进行回归分析,每天得到一个拟合模型,得到系数a和b随年积日变化的曲线图,如图3所示。
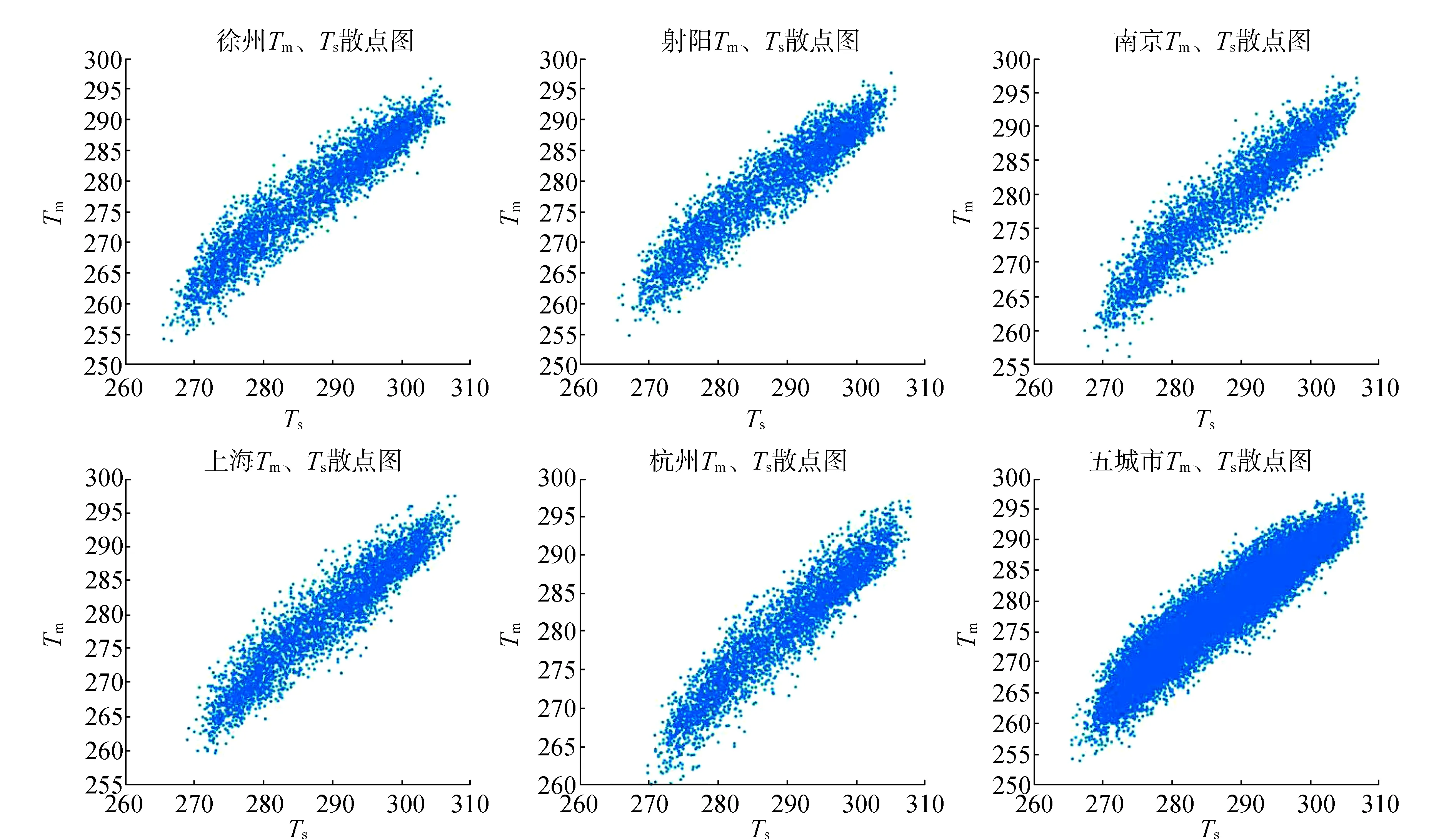
图2 Tm与Ts散点图

图3 系数a、系数b对应年积日散点图
由图3可以看出,系数a和系数b的变化趋势相反,但并无明显的年周期性,春季与夏季两个季度总体上系数a逐渐减小,但是秋冬两季该系数变化更为复杂。利用所选5个测站2016年的气象探空数据作为检验样本,利用实测的地表温度Ts以及对应的年积日拟合得到的系数a、b计算Tm,得到检验Rms为2.61 k,与Bevis公式及李建国模型的精度对比如表2所示。
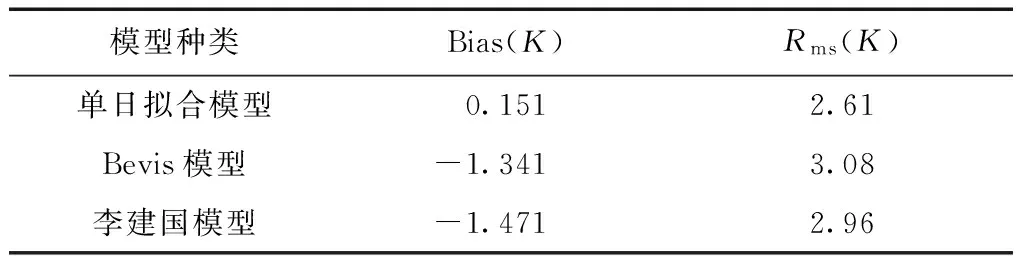
表2 3种模型精度对比表
由表2可知,单日拟合的模型精度较之Bevis模型及李建国模型分别提高了15%和12%。因此,顾及到年积日变化的分段线性模型能取得更高的精度。
3 江苏地区Tm分段线性模型的建立及其精度分析
由于单日的数据量有限,拟合得到的模型预测稳定性尚需进一步验证,因此本文设计了几个试验,分别采用3 d,8 d,15 d,30 d以及分季度拟合等5种拟合方案,并将之与Bevis以及李建国模型进行对比,得出结论如表3所示:
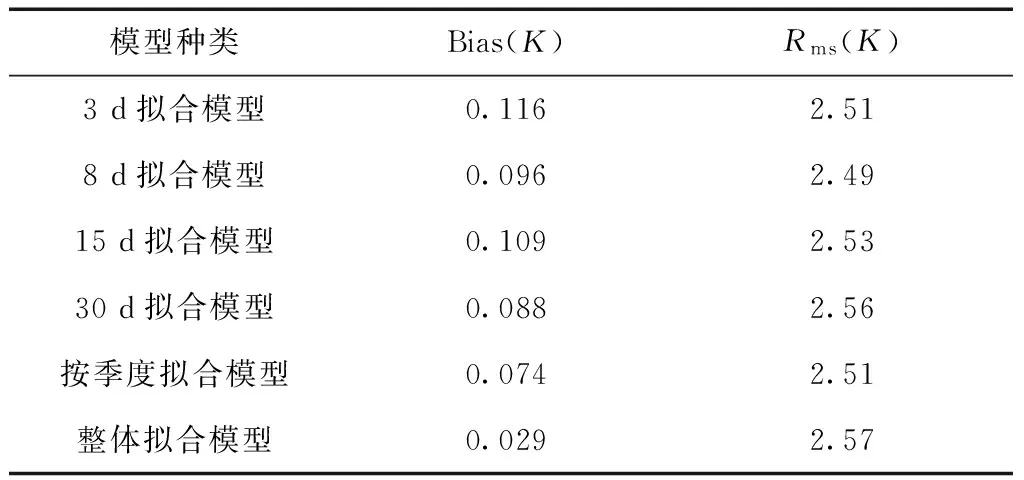
表3 几种拟合方案之比较
由表3可以看出,随着分段拟合每一段所选取的数据量的增加,回归模型的平均偏差有减小的趋势,但这一规律在Rms上并未得到体现,且按照每8 d的数据进行分组线性回归,得到的模型Rms最小,为2.49 K,比Bevis提高了19%,比李建国模型提高了16%。绘出8 d拟合分段线性模型的系数折线图如图4所示。
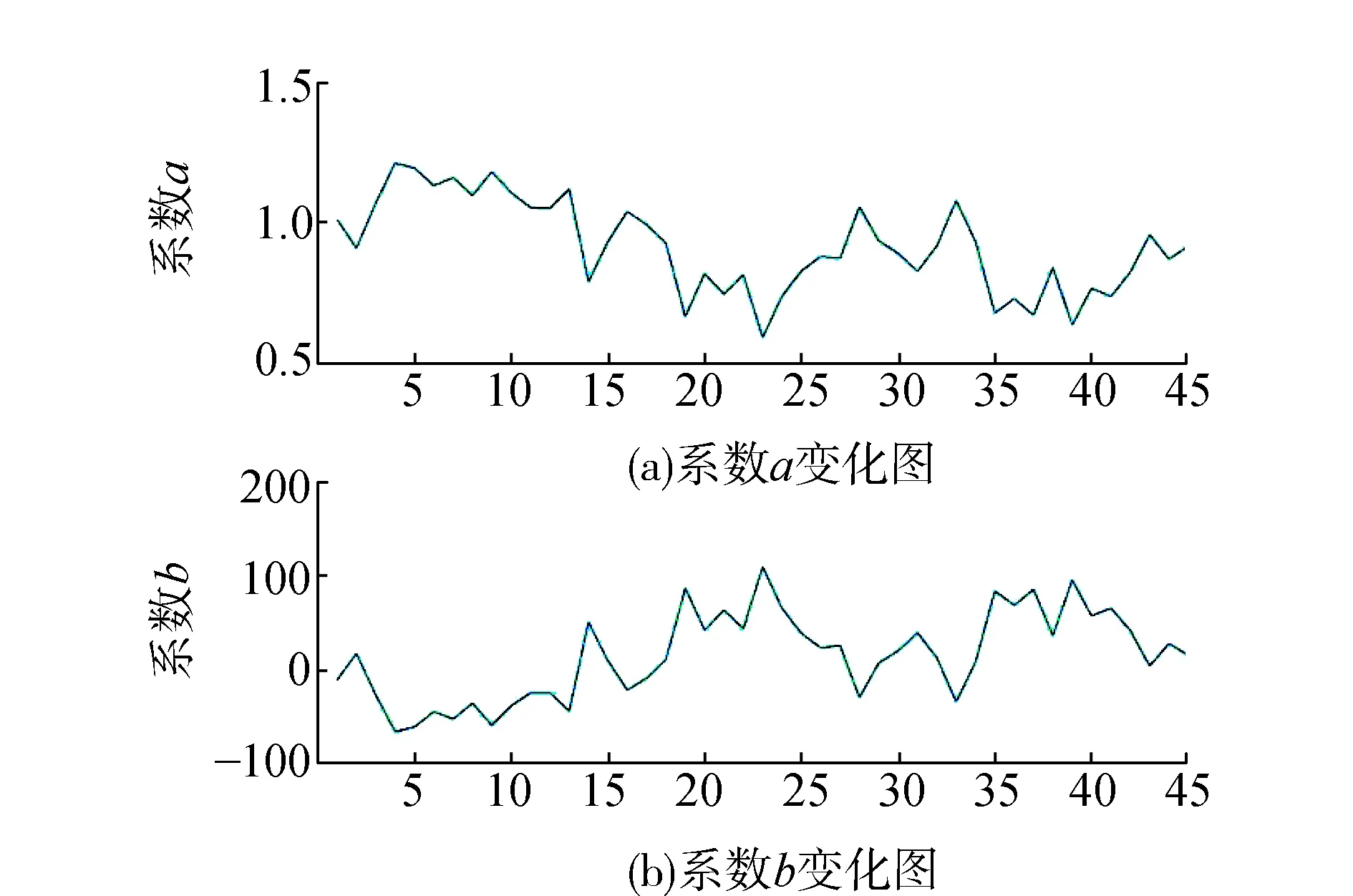
图4 8 d拟合模型的系数变化图
由图4可以看出,系数a和b的整体变化趋势与单日拟合的结果相似,春季和夏季两个季节系数a逐渐减小,到184 d左右降低到最小,同时秋冬两季系数a的变化波动较大,无明显规律。绘出8 d拟合模型计算得到的Tm值以及探空数据计算得到的Tm值的散点图,如图5所示。
由图4可知,采用8 d的数据进行分段线性拟合得到回归模型计算的Tm值与探空数据计算得到的精确Tm符合较好,且变化趋势也趋于一致。
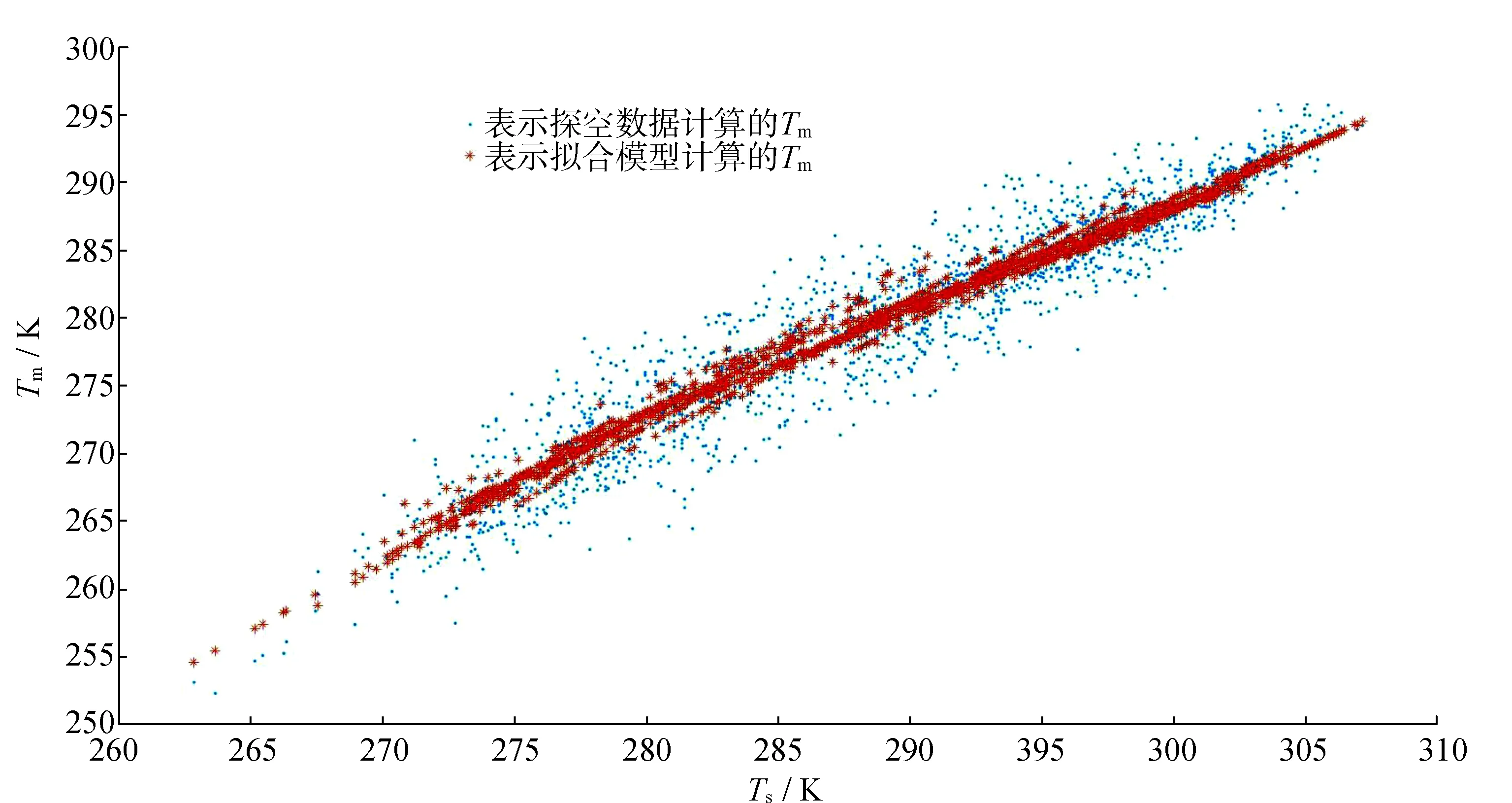
图5 Tm散点图
4 结 论
本文利用2005—2015年共11年的数据分析了江苏地区Tm与Ts的变化趋势,说明Tm与Ts之间线性关系随年积日存在的变化,同时分析对比了不同分段拟合的方案,建立了适合江苏地区计算加权平均温度的分段线性模型,具体结论如下:
1)局部大气Tm及Ts存在明显的年周期变化规律,同时在江苏地区Tm与Ts的变化整体上趋于一致,但是夏季与冬季线性相关性有所不同;
2)按年积日每日拟合得到一个回归模型,分析得到Tm与Ts线性相关特性随着年积日的变化有着明显的变化,但其整体的规律性不明显;
3)文章对比了几种分段线性回归方案,分段线性拟合模型外符合精度高于Bevis模型和李建国模型以及整体拟合线性模型,其中按照8 d一组进行拟合得到的分段线性模型外符合精度最好为2.49 K。
本文并未考虑Tm与Ts相关性与纬度等因素的影响,也并未对系数a和b做详细的时间序列分析,每8 d一个时段拟合,模型形式较为复杂,建模方法普适性尚待进一步提高。
参考文献:
[1] 李国平. 地基GPS气象学[M]. 北京:科学出版社, 2011:1-2.
[2] 龚绍奇. 中国区域大气加权平均温度的时空变换及模型[J]. 应用气象学报, 2013, 24(3): 332-341.
[3] 王晓英, 戴仔强, 曹云昌, 等. 中国地区GPS加权平均温度Tm统计分析[J]. 武汉大学学报(信息科学版), 2011, 36(4): 412-416.
[4] 李建国, 毛节泰, 李成才, 等. 使用全球定位系统遥感水汽分布原理和中国东部地区加权“平均温度”的回归分析[J]. 气象学报, 1999, 57(3): 283-292.
[5] BEVIS M. GPS Meterorology:Remote Sensing of Atmospheric Water Vapor Using the Global Positioning System[J]. J Geophys Res, 1992, 97(14): 15787-15801.
[6] 谷小平, 王长耀, 蒋国华. GPS水汽遥感中的大气加权平均温度的变化特征及局地算式研究[J]. 气象科学, 2005, 25(1): 79-83.
[7] LIOU Y A, TENG Y T, van HOVE T, et al. Comparison of precipitable water observations in the near tropics by GPS, microwave radiometer, and radiosondes. J Appl Meteorol, 2001, 40: 5-15.
[8] 青盛, 吕弋培, 黄丁发, 等. GPS水汽反演在成都地区的应用[J]. 四川测绘, 2008, 31(3): 121-123.
[9] 姚宜斌, 刘劲宏, 张豹, 等. 地表温度与加权平均温度的非线性关系[J]. 武汉大学学报(信息科学版), 2015, 40(1): 112-116.
[10] 王浩, 李国平. 成都地基GPS 水汽监测系统建设与应用[J]. 地球信息科学报, 2011, 13(2): 213-218.

