直升机卫星通信传输帧结构设计与分析

魏瑞刚

(中国电子科技集团公司第五十四研究所，河北 石家庄 050081)

0 引言

直升机经过近30年的发展，其飞行和作战性能不断提高，已经逐渐成为战场火力支援、武装侦察以及人员输送的主要力量。除此之外，由于我国地震、洪水和森林火灾等严重自然灾害频发，直升机因其具有快速、机动灵活和不受地理条件限制等特点，在抢险救灾过程中作为空中救援和侦察平台，得到了大量应用。

随着直升机的应用范围越来越广和任务复杂度不断提高，机地间的不间断通信、宽带数据传输和多空域的地面协同指挥的需求也逐渐增长，原有的机载通信手段难以满足这种要求。而卫星通信具有广域覆盖、受地理环境约束小、支持宽带组网通信和通信质量稳定等特点，可以很好地解决这一问题，因此研究卫星通信在直升机平台上的应用具有重要的意义。然而直升机卫星通信信号的传输会受到直升机旋翼遮挡的影响，文献[1]中给出了基于LMS估计的缝隙预测方案，该算法能够完成发生缝隙时刻的预测，但是在工程实现中检测的可靠性不高。文献[2]中给出了基于重发策略的抗旋翼遮挡方法，该方法的缺点也是传输效率较低。文献[3]中给出了基于信号检测的缝隙通信思想，利用缝隙间隔完成信号的传输，但复杂度较高。本文通过分析直升机卫星通信旋翼遮挡的特点，设计了一种信道高效传输的帧结构，该帧结构的信号捕获概率高，虚警概率很小，能够在不降低传输效率的前提下降低旋翼遮挡对信号捕获的影响，而且能够提高频率估计的频差范围。

1 直升机卫星通信旋翼遮挡问题

由于直升机物理结构的特点，导致直升机卫通天线只能安装在直升机旋翼的下方，其安装示意图如图1所示。从图1可见，直升机卫通天线在收发卫通信号时，会受到直升机旋翼的遮挡，在直升机飞行的过程中，旋翼周期性地遮挡天线面，造成机载接收信号的衰减。

信号遮挡的周期由旋翼转速和桨叶数决定，与直升机飞行航向和卫星的仰角和位置等参数无关。

T=1/(V×N)，

(1)

式中，T为遮挡周期(s)；V为旋翼转速(r/s)；N为桨叶的数量。

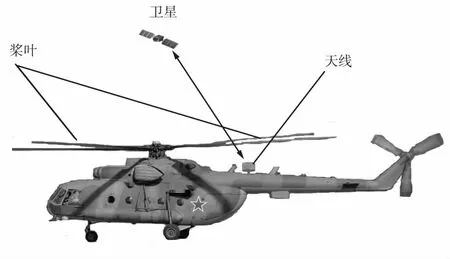
图1 直升机卫通天线安装示意

每个旋翼的遮挡时间可以近似依据式(2)决定，无遮挡时间近似依据式(3)决定，文献[1]中给出在不同的航向夹角β的情况下，旋翼对天线的遮挡时间长短的计算公式，可以用γ表示旋翼对天线的遮挡时间。

(2)

(3)

(4)

λ=h×cotα，

(5)

式中，d为天线与旋翼中心的水平距离；h为天线与旋翼中心的垂直距离；α为天线仰角。

在直升机旋翼下，用实时频谱仪采集的直升机旋翼遮挡的实测数据可以得到如图2所示的信号衰减模型，信号衰减周期为旋翼遮挡周期，信号衰减幅度约为18～20 dB。

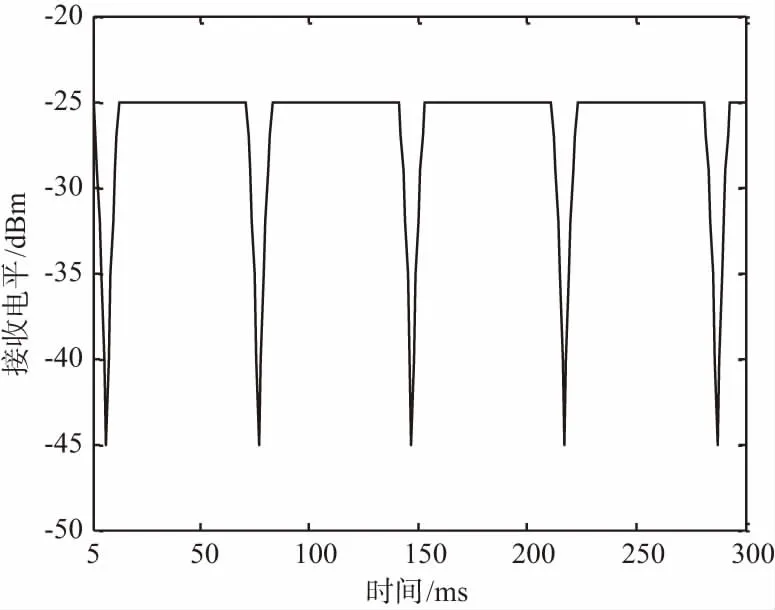
图2 旋翼遮挡信号衰减

2 前向链路帧结构设计

通过上述分析得知，在直升机旋翼遮挡下，机载接收机的接收信号功率会按照某种周期衰减，而接收信号功率的衰减势必会影响解调流程中信号的同步，而同步信息仅用来完成信道链路的同步，不传输任何业务信息，因此同步信息的长度会影响信道传输的效率，为了便于信道的同步，需要在传输的有效帧中周期插入同步信息，此外考虑信道的传输效率，要尽量减少同步信息插入的数量，平衡同步信息的数量和信道传输的效率是信号帧结构设计首先要考虑的问题，另外如果插入的信息能够被多个功能利用，同样会达到最优设计的目的。鉴于以上目的，本文设计了一种帧结构，其结构示意图如图3所示，通过传输该帧结构的信息，机载解调器能够在接收信号被旋翼周期遮挡的条件下正确完成信号的解调。

图3 帧结构示意

图3中，每个物理帧由数据帧S和导频帧P组成，其中每个数据帧S由30个符号比特构成，而导频帧P是由2种PN码P1和P2组成，其中P1为周期是128的伪随机码序列，P2为周期为220的伪随机码的截短序列，信道数据的捕获主要由导频帧P1来完成，频率同步和相位同步主要由P1和P2共同来完成。假定设计的系统编码帧长度为16 200 Bit，则一帧数据中需要插入的导频比特共有540 Bit，这样帧效率可达97%，满足传输系统的要求。

针对以上设计的帧结构，系统的解调同步可以按照如下方法进行：首先对帧结构中的数据信息和导频信息利用傅里叶变换的方法完成初始的大频偏估计，对信号的大频偏做一校正；然后再利用插入的导频信息做二次频率估计，完成对残余频偏的频偏校正，确保最后的频差能够满足载波相位跟踪的要求；最后利用相位内插法完成载波的相位同步。

采用以上帧结构的设计方法具有以下优点：

① 用来捕获的导频信息分散地插入数据比特中，在低速信号的传输中，降低了旋翼遮挡对信号捕获的影响；

② 解调同步共用了用来捕获的导频信息，提高了信道传输效率；

③ 采用已知的导频信息做频率同步，提高了频率估计的频差范围。

基于在旋翼遮挡的条件下，信号捕获和频率跟踪在解调流程中的重要性，下面重点对信号的捕获技术和频率跟踪技术做详细分析。

3 信号捕获技术分析

信号的捕获采用基于匹配滤波器的捕获算法，算法原理框图如图4所示。

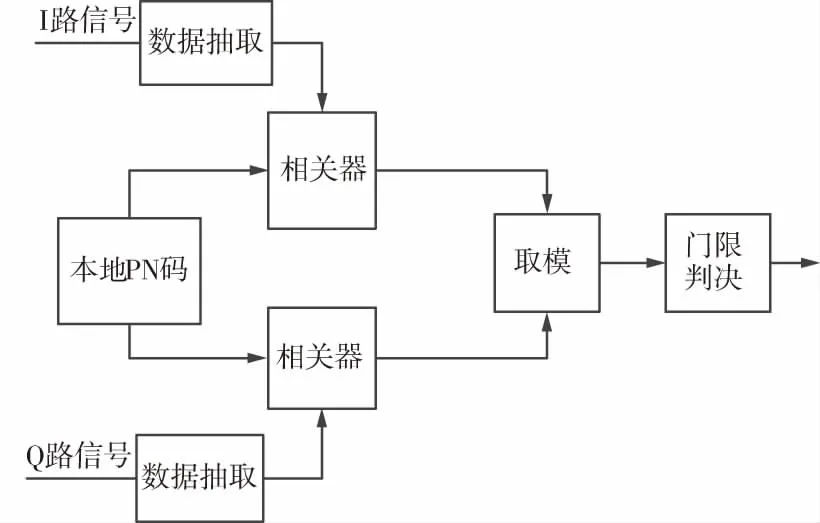
图4 信号捕获算法原理

接收到的IQ信号进入数据抽取模块，按照每隔30个符号抽取一次的规则进行运算，抽取后的IQ数据分别与本地PN码产生的伪随机序列做相关运算，将相关运算后的数据取模并且与设定的判决门限值做比较，进而完成整个捕获过程。

由最佳接收的理论可知，对于接收信号s(t)，其匹配滤波器的冲击响应为：

h(t)=s(T-t)，

(6)

式中，T为信号s(t)的持续时间，滤波器的输出为：

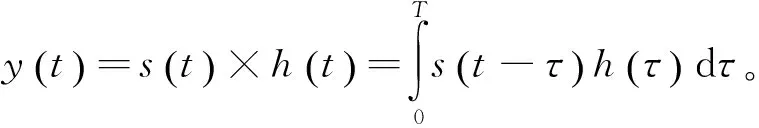
(7)

假设数字匹配滤波器的输入信号的采用速率为fs，滤波器的级数为N，则式(7)对应的离散形式为：

(8)

h(kTs)=PN(NTs-kTs)。

(9)

在实现过程中，把式(9)中的h(kTs)看作滤波器的系数，可以设置成PN码序列{c0，c1，c2，…，cN-2，cN-1}。

在捕获时，接收到的信号与本地信号进行相关运算，可以将本地的PN码序列作为固定的滤波器系数，让接收到的信号进入滤波器中，每一时刻都会得到一个相关值，当2个序列的相位一致时，会出现一个相关峰，如果相关峰的大小超出给定的门限值，则信号捕获成功，另外可以在门限判决模块中加入一种控制策略来减小在旋翼遮挡的条件下信号捕获的漏警概率。

下面通过仿真的手段来分析捕获门限的选取及捕获虚警的概率。

仿真条件：QPSK调制，8倍采样，Es/N0为3 dB，归一化频偏为1/32，成型滤波器和匹配滤波器的滚降系数β=0.35的平方根升余弦滤波器，归一化时钟偏移为1/8，归一化频偏为1/32。

门限仿真图如图5所示。从图5可以看到，本地码与捕获码字对齐与不对齐的情况下，相关值分界分明，门限比较容易设置。

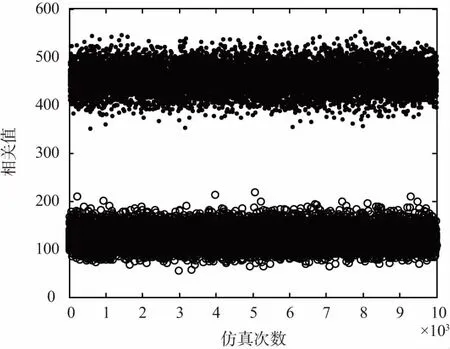
图5 捕获门限仿真

下面分析在不同的频偏条件下信号的捕获概率和虚警概率。假设如下仿真条件：符号Es/N0设为3 dB，判决门限设为280，旋翼遮挡周期为62.5 ms，遮挡比例为20%，归一化频偏以1/27的步进在[1/27，1/23]内变化，每个归一化频偏样点蒙特卡洛仿真10 000次，得到的捕获和虚警概率如表1所示。从表1可以看出，在整个归一化频偏区间内，虚警概率不大于0.1%，在工程实现上，这个概率在可允许的范围内。

表1 不同频偏下捕获概率和虚警概率

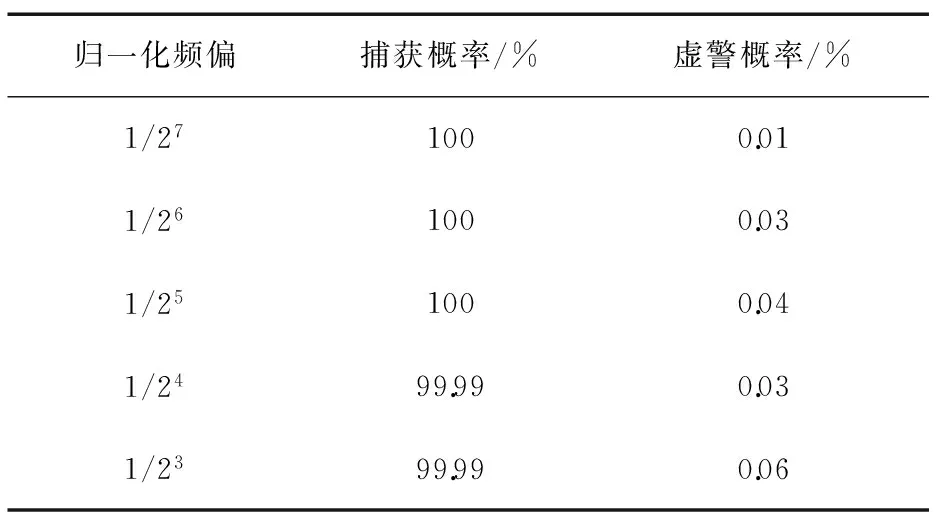
归一化频偏捕获概率/%虚警概率/%1/271000.011/261000.031/251000.041/2499.990.031/2399.990.06

下面分析在不同的信噪比条件下，信号的捕获概率和虚警概率。假设如下仿真条件：归一化频偏为1/25，判决门限设为280，旋翼遮挡周期为62.5 ms，遮挡比例为20%，Es/N0以1 dB的步进在[0 dB，5 dB]范围内变化，每个Es/N0样点蒙特卡洛仿真1 000次，得到相应的捕获和虚警概率如表2所示。从表2可以看出，Es/N0大于3 dB时，捕获概率可达100%，虚警概率小于0.1%，满足实际的工程需求。

表2 不同符号信噪比下捕获概率和虚警概率

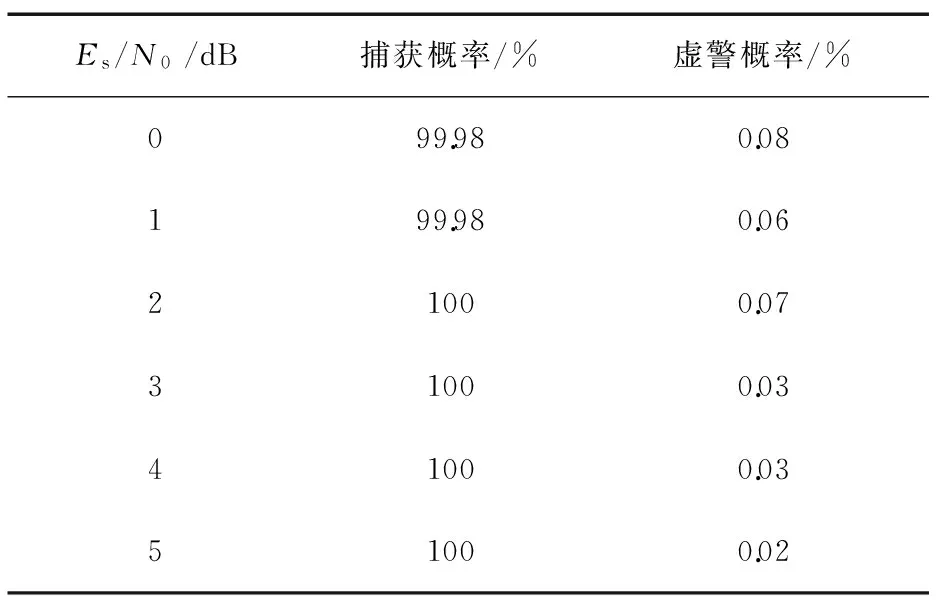
Es/N0/dB捕获概率/%虚警概率/%099.980.08199.980.0621000.0731000.0341000.0351000.02

4 频率估计技术分析

本文在帧结构的设计中，考虑了系统的频偏估计问题，频偏估计的原理框图如图6所示。

图6 频率估计原理

以QPSK调制方式为例，数据处理模块首先对输入数据作4次方运算，并对运算后的数据进行存储。当累计存储4096点后用高速时钟发送给FFT模块做FFT变换。

假设QPSK调制信号为：

s(t)=A×exp(jθM)exp[j(2πΔf+θ)]，

(10)

式中，θM为QPSK的调制相位，θM=π/4×N(N=0，1，2，3)；Δf为信号频偏；A为调制信号幅度。对其进行4次方运算之后，

s(t)4=A4exp(j×4×θM)×

exp[j×(2π×4×(Δf+θ))]=

A4exp[j×(2π×4×(Δf+θ))]。

(11)

变换之后的信号为一频率为4Δf的正弦信号，理论上对其进行FFT运算后会在4Δf的频点出现最大幅度谱线。因此，根据FFT运算后最大值的位置可以计算出信号偏移。

假设如下仿真条件：调制方式为QPSK，归一化频偏为1/64，在门限信噪比Es/N0=3 dB，旋翼遮挡周期为62.5 ms，遮挡比例为20%，FFT长度为4 096条件下通过FFT计算出的频偏仿真图如图7所示。从图中可以看出，最大点的位置出现在第257个点处，则仿真出的频偏为257/(4 096×4)=1/63.75，其估计的归一化精度可达1/(4 096×4)，经过前文所述的二次估计后归一化精度可达1/106，满足工程的需求。

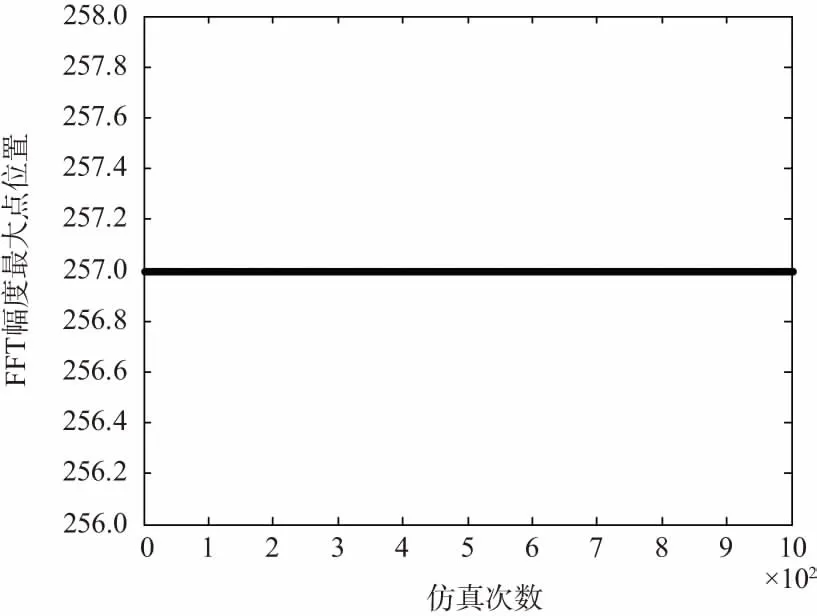
图7 频率估计仿真结果

5 结束语

在直升机卫星通信系统的应用背景下，在帧内插入导频信息解决了直升机旋翼遮挡对信号接收的影响，而且满足所设计帧结构的信号捕获概率高，错捕概率较低，并且具有较高的频率估计精度。由于该算法具有通用性，能够适应不同型号的直升机，因此该设计方法具有极强的实际使用价值，给出的原理框图可以指导工程实现。

[1] 匡麟玲，倪祖耀，凡明清.一种基于LMS的直升机旋翼缝隙时间预测方法及装置：CN102521503A[P],2012-06-27.

[2] 董孝东.直升机卫星通信中旋翼遮挡问题及应对方法[J].现代电子技术，2014，34(7)：42-48.

[3] 姚国义，张德华.一种直升机旋翼遮挡缝隙检测方法[J].无线电通信技术，2014，40(3)：36-38.

[4] 吴团锋，杨喜根，李际平.一种基于FFT的联合帧同步和频偏估计算法[J].电子与信息学报，2006，28(5)：840-843.

[5] 赵树杰.信号检测与估计理论[M].西安：西安电子科技大学出版社，1998：202.

[6] 潘亚汉，朱自强，张志强.现代卫星通信调制解调技术的发展[J].微波与卫星通信，1997(4)：11-15.

[7] 张厥盛，郑继禹，万心平.锁相技术[M].西安：西安电子科技大学出版社，2000：86-89.

[8] 张润峰.低信噪比条件下的载波恢复[D].长沙：国防科学技术大学，2007：23-24.

[9] 黄振，陆建华，杨士中.卫星通信中多普勒频移的快速捕获[J].电子学报，2003，31(7)：1052-1057.

[10] XIONG Fuqin.Modem Techniques in Satellite Communications[M].IEEE Journals & Magazines，1994,32(8)：84-98.

[11] ERUP L，GARDNER F M，HARRIS R A.Interpolation in Digital Modems-Part II：Implementation and performance[J].IEEE Trans.Comet.，1993，41(6)：998-1088.

[12] HOGENAUER E B.An Economical Class of Digital Filter for Decimation and Interpolation-I：Analysis and Design[J].IEEE Trans.on Acoustics，Speech and Signal Processing，1981，ASSP-29(2)：155-162.

[13] MITOLA J.The Soft Radio Architecture[J].IEEE Communications Magazine，1995(5)：26-39.

[14] 樊昌信，詹道庸，徐炳祥，等.通信原理(第4版)[M].北京：国防工业出版社，1995.

[15] 潘申富，张丽娜.一种低信噪比解调的实现方案及性能仿真[J].无线电通信技术，2011，37(2)：55-58.

[16] WOLEJSZA H，CACCIAMANI M.Identification of QPSK Modulation System Phase Ambiguity[J].IEEE Communications Magazine，1996(2)：251-259.

[17] 潘申富.基于频带共享的卫星通信关键技术研究[D].北京：北京大学,2003：12-28.

[18] 张健.软件无线电的基本理论构架[R].成都：电子科技大学，2000.

[19] MELO A G，SILVA H J A D.Improved Performance QPSK Demodulator for Digital Satellite Radio[C]∥IEEE Comm，2000：94-108.

[20] 樊昌信，曹丽娜，通信原理(第6版)[M].北京：国防工业出版社，2011：65-72.