适用于高阶QAM信号的分数间隔混合盲均衡算法
谢春磊,王晓亚
(1.中国电子科技集团公司第五十四研究所,河北 石家庄 050081;2.装备工程技术研究实验室,河北 石家庄050081)
0 引言
QAM调制具有较高的频谱利用率,随着现代科技的发展,人们对通信容量的要求日益增大,越来越多的领域采用QAM调制,并且使用的调制阶数也越来越高。信道带宽限制和多径传播等会引起码间干扰,这种干扰对高阶QAM信号的影响更大,接收端需要引入均衡技术。利用训练序列进行均衡[1],可以取得较好的性能,但牺牲了传输性能[2]。1975年,Sato提出了盲均衡的思想[3],它不需要额外的训练序列,扩大了均衡技术的应用范围,因此受到了研究人员的广泛关注。
在各类盲均衡算法中,Godard[4]提出的恒模算法(CMA)以其计算简单、鲁棒性强而得到了广泛应用。然而传统的CMA算法收敛速度慢、稳态误差大,当应用于高阶QAM信号时,该缺点更加明显。因此,以CMA算法为基础,研究人员又提出了精简星座盲均衡算法(RCA)[5]、多模盲均衡算法(MMA)[6]以及基于多模式的混合盲均衡算法[7]。高阶QAM调制下,MMA算法收敛性能优于CMA算法,并解决了CMA算法的相位模糊问题;混合盲均衡算法一般先使用CMA等盲均衡算法实现收敛,然后再切换到其他均衡算法,以减小稳态误差[8]。
本文提出了一种适用于高阶QAM信号的分数间隔混合盲均衡算法,先使用CMA算法进行均衡器的初始训练,然后再切换到直接判决LMS算法。为了消除CMA算法的相位模糊,将均衡结构与载波跟踪环路相结合;为加快CMA算法的收敛速度,采用时域解相关的方法来更新均衡器系数。
1 混合盲均衡算法
1.1 系统模型
混合盲均衡的系统框图如1所示。经过信道以后,均衡器的输入信号表达式为:
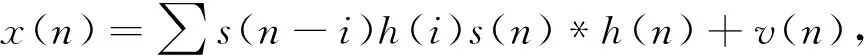
(1)
式中,s(n)为等效复基带信号,满足s(n)=sr(n)+jsi(n);h(·)为等效信道冲激响应,是由发送方、接收方和传输信道共同决定的;v(n)为加性高斯白噪声,均值为0,方差为σ2。
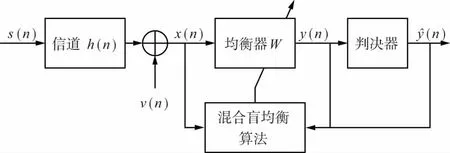
图1 混合盲均衡系统模型
均衡器一般采用FIR结构,则输入输出关系可以表示为:
(2)
式中,y(n)为均衡器输出信号;X(n)=(x(n),x(n-1),…,x(n-M+1))T为均衡器的输入向量;W(n)=(w0(n),w1(n),…,wM-1(n))T为均衡器抽头系数向量;M为均衡器的阶数;上标*表示共轭运算;上标H表示共轭转置运算。
均衡的目的是将y(n)作为s(n)的最佳估计,从而消除信道不平坦、多径等带来的影响。从公式来看,就是按照一定的规则调整抽头系数W(n),使得W(n)*h(n)满足奈奎斯特准则[9],使得判决时刻的码间串扰最小。混合盲均衡算法综合利用调制信号的统计特征和瞬时特征,因此较单纯的盲均衡算法具有更好的均衡性能。
1.2 分数间隔CMA算法
CMA算法利用调制信号的统计特征来调整抽头系数,它对载波频偏不敏感,非常适用于信号初始接收阶段,相应的误差提取和系数更新公式为:
e(n)=y(n)(|y(n)|2-R2),
(3)
W(n+1)=W(n)+μe(n)X*(n),
(4)
式(3)中,R2为由调制样式确定的常数,由式(5)确定;式(4)中,μ为系数更新步长。
(5)
式中,a(k)为标准星座图中的复数星座点。
分数间隔CMA算法,在接收端以小于码元周期T的间隔对接收信号进行过采样,与整符号间隔CMA算法相比有更快的收敛速度和更小的稳态精度。从频域定性分析其原因:QAM调制信号采用滚降系数为α(0<α<1)的成型滤波器,复基带信号的有效带宽B=(1+α)/(2T);当采用整符号间隔均衡算法时,等效于采样间隔为T,按照低通抽样定理,对应的无失真信号带宽B′=1/(2T),显然B′
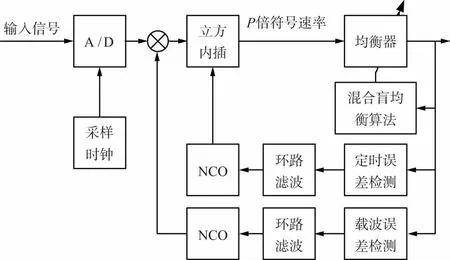
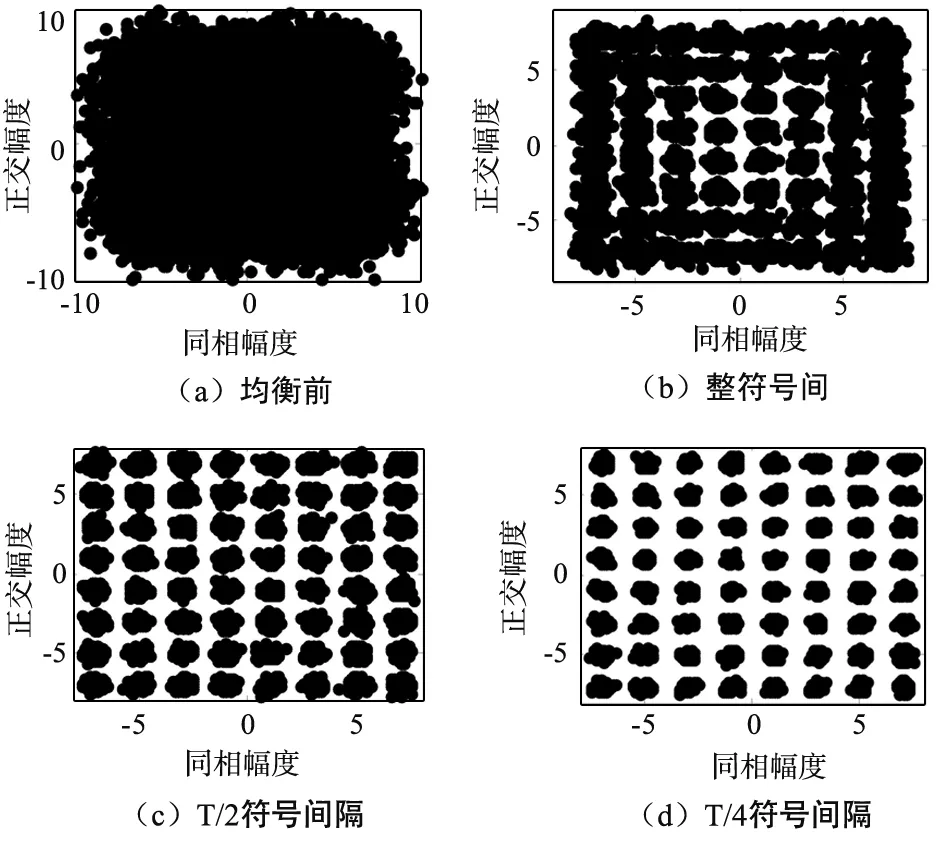
分数间隔CMA算法对应的多信道模型[10]如图2所示,均衡器间隔为T/P,P是正整数,表示过采样倍数。其中,x(i)(n)=x(nT+iT/P),0≤i y(i)(n)=W(i)H(n)X(i)(n), (6) (7) 图2 分数间隔CMA算法模型 时域解相关可以有效提高均衡器的收敛速度[11-13]。均衡器的输入信号之间有高度的相关性,而分数间隔均衡器的相关性更强,这会降低均衡器的均衡性能。输入向量X(n)与X(n-1)在n时刻的相关系数为: (8) α(n)越大表明X(n)与X(n-1)之间的相关性越强。 从X(n)中减去α(n)X(n-1),得到 Z(n)=X(n)-α(n)X(n-1), (9) 为时域解相关后的结果,该结果可以与卡尔曼滤波的新息相类比[14],将其作为新的迭代更新向量,将式(4)改写为: W(n+1)=W(n)+μe(n)Z*(n)。 (10) 随着分数间隔CMA均衡算法的迭代,均衡器的输出逐渐收敛、稳定,需要切换到基于判决的LMS算法,以获得更好的稳态性能,LMS算法的误差提取公式为: (11) (12) 式中,η体现了对输入数据的记忆性,反映了估计算法的跟踪能力,一般取0.99。 这样,均衡器系数更新公式可以综合写为: (13) 式中,β(n)与MSE的关系为: (14) 式中,d表示QAM星座图中的判决区域中点离对应的判决星座点的距离最大值。 按照软件无线电的思想,通用接收机的采样率与符号速率之间可能不满足整数倍关系。由采样定理可以知道,只要采样率大于信号带宽的2倍便可以实现信号的无失真接收。因此,后续处理往往采用内插的方法进行重采样;另外,结合经典的Gardner定时误差提取算法[17],重采样后的速率一般为符号速率的2倍。这样,在对现有处理流程改变不大的前提下,可以直接使用T/2符号间隔均衡结构。T/P符号间隔均衡通用数字接收机处理流程如图3所示。 图3 通用数字接收机均衡处理流程 图3中定时同步环路用于控制立方内插的位置,保证获得的内插样点与符号周期起始时刻的偏差为T/P的整数倍;而载波同步环路用于校正信号的载波误差,从而弥补CMA均衡算法的不足[18-19]。 从以下3个方面对本文的混合盲均衡算法性能进行性能仿真分析、比较: ① 不同分数间隔均衡算法的性能; ② 时域解相关对均衡性能的影响; ③ 与CMA均衡算法、LMS均衡算法的性能进行比较。 在信噪比为30 dB时,针对64QAM调制信号进行仿真试验,观察不同分数间隔均衡对星座图的恢复情况。分数间隔时均衡器长度为5阶,初始化中心抽头系数为1,其他抽头系数为0。 图4(a)为没有进行均衡时的同步输出结果,可以看出是方形的星座分布,但由于信道引入了码间干扰,星座点难以收敛;图4(b)、图4(c)和图4(d)依次为整符号间隔、T/2符号间隔和T/4符号间隔均衡后星座点收敛情况,由于加入了载波相位同步环路,消除了CMA均衡算法的相位模糊;符号间隔越小,均衡效果越好。后续仿真发现,当符号间隔小于T/4时,均衡效果没有明显的提升,因此没有必要消耗更多的运算资源。 图4 64QAM信号均衡后星座图 仿真对比有无时域解相关对均衡性能的影响,以评价其对均衡性能提升带来的贡献。仿真条件同3.1节,按照式(12),对比有无时域解相关时均方误差曲线MSE的变化,如图5所示。从收敛速度来看,加入时域解相关后均衡器有更好的收敛性能;从稳态误差来看,加入时域解相关后均衡器的稳态误差更小、更平滑。因此,时域解相关处理不仅加快了收敛速度,还提高了稳态性能。 图5 有无时域解相关时MSE曲线 混合盲均衡算法综合利用了信号的统计特征和瞬时特征,CMA算法仅利用了统计特征,LMS算法则仅利用了瞬时特征,仿真对比三者的性能,可以了解综合利用2种信号特征对均衡性能的影响。在信噪比为30 dB的情况下,对比三者的均方误差曲线MSE。从收敛速度来看,混合算法、CMA算法的收敛速度比LMS算法要快,这是因为在初始状态下,瞬时特征的误差较大,导致对均衡系数的有效调整少;但从稳态误差来看,混合算法、LMS算法的性能比CMA算法要好,这可以解释为当MSE较小时,瞬时特征比统计特征提供的误差信息更加精确。因此,混合算法充分利用了初始阶段更加稳定的统计特征和稳定阶段更加精确的瞬时特征。3种算法的MSE曲线如图6所示。 图6 3种算法的MSE曲线 用分数间隔均衡器结构来实现混合盲均衡算法,并引入时域解相关,提高了均衡的稳态性能,加快了均衡的收敛速度。该结构应用于通用解调器的接收,对现有同步环路的改动不大,便于工程应用。需要指出的是,本文仅对方形星座图的高阶QAM信号接收性能进行了充分仿真、验证,对其他星座图分布的QAM信号均衡性能还需要做进一步的分析。 [1] 刁树林,钟剑波.时域自适应均衡技术的分析与应用[J].无线电工程,2009,39(9):44-47. [2] 张贤达,保铮.通信信号处理[M].北京:国防工业出版社,2002:226-257. [3] SATO Y.A Method of Self-recovering Equalization for Multilevel Amplitude Modulation Systems[J].IEEE Transactions on Communications,1975,23(6):679-682. [4] GODARD D.N.Self-recovering Equalization and Carrier Tracking in Two-dimensional Data Communication System[J].IEEE Transactions on Communications,1980,28(11):1867-1875. [5] 张凯,于宏毅,胡赟鹏,等.稀疏信道下基于稀疏贝叶斯学习的精简星座盲均衡算法[J].电子与信息学报,2016,38(9):2255-2260. [6] YANG J,WERNER J J,DUMONT G A.The Multimodulus Blind Equalization and Its Generalized Algorithms[J].IEEE Journal on Selected.Areas in Communications,2002,20(5):997-1015. [7] 王彬,葛临东,霍亚娟.适用于高阶QAM信号的多模混合盲均衡算法[J].数据采集与处理,2011,26(1):8-14. [8] 戴诚,梁诗晨,肖静薇,等.基于分数间隔的双模式盲均衡算法研究[J].无线电通信技术,2016,42(6):59-62. [9] 张辉,曹丽娜.现代通信原理与技术[M].西安:西安电子科技大学出版社,2006. [10] 孙守宇,郑君里,徐忠勇,等.修正恒模算法分数间隔盲均衡[J].电子学报,2003,31(11):1732-1735. [11] 龙剑友,王梓展,夏舜晖,等.一种解相关变步长归一化LMS自适应算法[J].计算机工程与科学,2006,28(4):60-62. [12] 贺洪江,王春霞.一种新的LMS自适应滤波算法分析仿真研究[J].传感器与微系统,2012,31(3):15-17. [13] 王晓东.一种分数间隔解相关修正判决反馈盲均衡算法研究[J].航天电子对抗,2012,28(4):56-58. [14] 陆光华,彭学愚,张林让,等.随机信号处理[M].西安:西安电子科技大学出版社,2003:50-57. [15] HE L,AMIN G,REED C,et al.A Hybrid Adaptive Blind Equalization Algorithm for QAM Signal in Wireless Communications[J].IEEE Trans.On Signal Processing,2004,52(7):2058-2069. [16] 许小东,戴旭初,徐佩霞.适合高阶QAM信号的加权多模盲均衡算法[J].电子与信息学报,2007,29(6):1352-1355. [17] GARDNER F M.A BPSK/QPSK Timing Error Detector for Sampled Receivers[J].IEEE Transactions on Communications,1986,41(5):998-1008. [18] 张华冲,王晓亚.适用于QAM信号的载波同步与均衡实现[J].无线电工程,2010,40(5):27-29. [19] 李红,雷志勇.基于最大熵谱估计的回波信号检测技术研究[J].半导体光电,2011,32(5):728-732.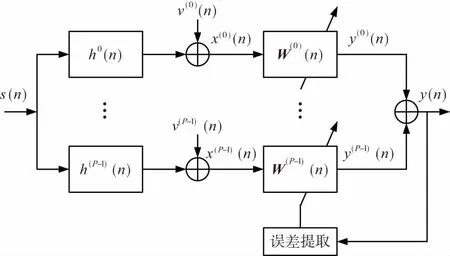
1.3 时域解相关
1.4 切换到LMS算法


2 算法实现
3 性能仿真与分析
3.1 不同分数间隔的均衡性能
3.2 时域解相关对均衡性能的影响

3.3 与单纯CMA、LMS算法性能比较

4 结束语

