舰载遥测装备伺服系统抗船摇设计与试验

李海鹏，于军亮

(中国人民解放军92941部队，辽宁 葫芦岛 125000)

0 引言

舰载遥测装备伺服系统不同于陆地伺服系统，需要进行抗船摇设计[1]。舰船在海上受风浪影响而不断产生随机运动，引起天线伺服系统位置和姿态的无规律变化，而地面系统并无此随机运动，因此要克服船摇产生的随机运动。目前常采用陀螺稳定策略隔离船摇对天线伺服系统的影响[2]。陀螺稳定策略主要利用天线俯仰臂上速率陀螺敏感出天线方位俯仰速率进行闭环控制，进而隔离船摇，该环路不足之处在于，天线轴主动运动时，它也进行动态抑制，降低了天线轴的反应速度，从控制概念上，一个物理量进行2次闭环控制是不必要的[3-4]。

实现伺服系统的稳定跟踪，伺服系统闭环采取以下2种方式：① 在自动跟踪工作方式下，通过速率陀螺信号前馈加船摇速度补偿进行跟踪环路闭环[5]；② 在数字引导等工作方式下，根据指令角和角度反馈进行位置环路闭环。2种工作方式原理类似，但输入信号不同，需要用不同的方法进行设计。利用船上惯导设备采集的船摇速度信息进行坐标变换，得出天线伺服系统方位俯仰轴的速度环路补偿量，实现船摇速度补偿算法，并在实际系统中进行了验证。

1 跟踪环抗船摇设计

跟踪环抗船摇采用速率陀螺信号前馈加船摇速度补偿方案进行设计，跟踪环路自身具有一定的船摇隔离度，速率陀螺信号前馈方案具有一定的船摇隔离度，整个跟踪环路的船摇隔离度为二者之和[6]。

1.1 跟踪环自身的船摇隔离度

伺服系统在扰动条件下的自跟踪环路框图如图1所示。

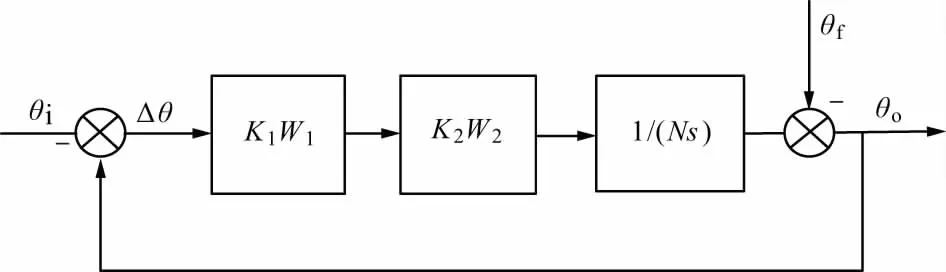
图1 扰动条件下的跟踪环路框图

图1中，θi为目标位置角度；θo为天线指向位置角度；Δθ为角误差；K1W1为位置环校正环节传递函数；K2W2为速度环闭环传递函数；1/(Ns)为电机速度到天线位置的传递函数；θf为船摇扰动信号。

图1中，天线指向角θo对目标位置θi是随动关系，而船摇θf是对θo的扰动。系统的作用是使输出量θo随动输入量θi，而且要克服θf的扰动。θi变化时，θo也必须跟随变化，其误差Δθ必须控制在规定的范围之内，这就是随动过程。安装在甲板上的天线座，因和船体一起摇摆，直接改变了天线的指向角θo(相当有θf扰动加入)，从而使Δθ增加，通过跟踪环路的调整，θo仍应随动θi。θf引起的Δθ也必须在允许的范围之内[7]。扰动是通过天线在甲板的运动改变了θo的指向，自跟踪环路的作用是使天线轴的运动方向与扰动方向相反，以保证Δθ在规定的范围之内，这就是自跟踪环路克服船摇扰动的过程。工程中通常应用简化形式计算隔离度[8]：

Lz≈20lg1/(1+K)=20lg1/(1+16.7)=-25 dB。

一般跟踪环自身的船摇隔离度实测值在20 dB左右，设计值与其相符，也说明上述设计计算的合理性。但是船摇隔离度的系统指标是40 dB，需要在跟踪环路增加专门的船摇隔离措施，即下面讨论的速率陀螺信号前馈方案。

1.2 速率陀螺信号前馈的船摇隔离度

速率陀螺信号前馈属于自动控制理论中前馈复合控制技术的扰动信号前馈方法[9]。通过扰动信号的前馈，可以达到理想的隔离效果。系统环路框图如图2所示。

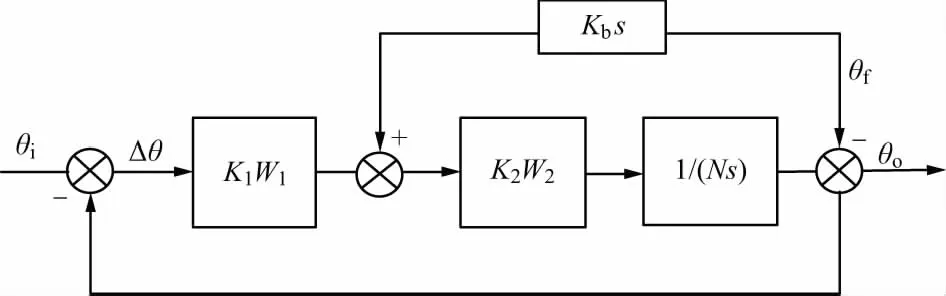
图2 含速度前馈的自跟踪环框图

图2中，Kbs为速率陀螺前馈补偿传递函数；Kb为补偿系数。

根据叠加定理，系统可以看作由θi、θf两个输入分别对输出的作用，再进行叠加。据此对系统框图进行等效变换，如图3所示。

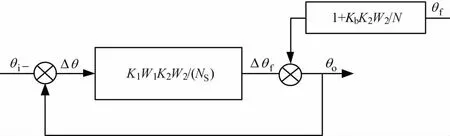
图3 含速度前馈的自跟踪环等效框图

图3中，Δθf就是船摇干扰θf对系统输出的影响，令Wb=1+KbK2W2/N，则船摇隔离度为：

Lb=20lgΔθf/θf=20lgWb。

若使得Wb=-N/(K2W2)，则Lb=-∞，船摇完全被隔离,这显然是做不到的，不可能令Kb精确到和-N/(K2W2)完全相等[10]。即使可以精确到相等，由于前馈引入的噪声，系统也不可能将干扰全部隔离。在工程中，通常设计Kb为一常数，即只有速度信号前馈，而不含加速度和更高阶信号的前馈，通过调整Kb的取值，可以得到满足指标要求的设计方案。即调整Kb的取值，使Lb≥30 dB,则L=Lz+Lb≥50 dB，满足指标要求。该方法在工程实践中取得了理想的船摇隔离效果。

2 位置环抗船摇设计

这里的位置环指的是在数字引导等工作方式下，系统根据指令角和反馈角的差值进行闭环控制的方式[11]。

在数字引导工作方式下，指令角由船上中心机给出，是根据目标位置和惯导给出船的位置解算出的大地角。天线控制单元需要根据惯导给出的船摇姿态信息[12]，将大地角解算成在船上的实际指向角，也就是甲板角。只要数据源和解算速度足够快，船摇就被隔离。实际情况中10 ms接收一帧数引数据，闭环周期也是10 ms，一次坐标系转换在一个闭环周期内完成，在这样的条件下船摇被隔离，伺服系统可以在数字引导工作方式下准确跟踪目标。

可见，位置环抗船摇方案的关键是大地角到甲板角的坐标系转换。由大地角转换为甲板角的公式如下[13]：

Aj= arctan(sinθ×sinψ×cosEd×cos(Ad-Kc)-cosθ×

sinψ×sinEd+cosψ+cosψ×cosEd×sin(Ad-Kc))/

sinEd×sinθ+cosEd×cosθ×cos(Ad-Kc)

Ej= arcsin(cosEd×sin(Ad-Kc)×sinψ+cosθ×cosψ×

sinEd-cosEd×sinθ×cosψ×cos(Ad-Kc))，

式中，Ed为大地俯仰角；Ad为大地方位角；ψ为船摇的横摇角；θ为船摇的纵摇；Kc为航向角；Ej为甲板俯仰角；Aj为甲板方位角。

3 试验与结果分析

通过实例，对船摇隔离度指标进行实测验证。舰船生减摇鳍模拟高海况下船体摇摆，为保证测试结果更加有效，舰船与目标来向尽可能呈90°夹角，即方位甲板角在90°附近，此时方位轴受船摇影响较小，俯仰轴受船摇(横摇)影响最严重[14]，俯仰轴的船摇隔离度可作为船摇隔离度的指标依据[15]。

3.1 减摇鳍生摇数据分析

减摇鳍生摇主要生横摇，减摇鳍最大输出能力下的横摇变化曲线如图4所示。

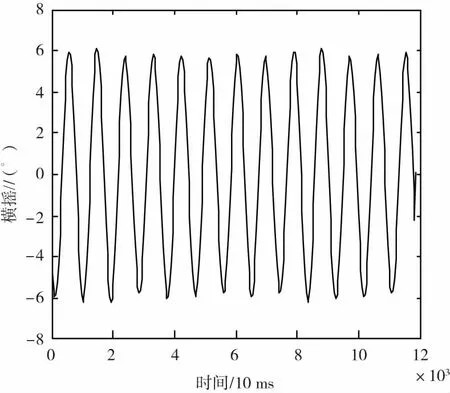
图4 减摇鳍最大输出能力的横摇变化曲线

从图4中可以看出，横摇角呈正弦规律变化，周期略高于10 s，横摇变化幅度超过12°，经多次生摇，结果均相同。此时天线伺服系统遭遇的船摇最恶劣[16]，船摇隔离度在该船摇下测试。

3.2 跟踪环路测试数据分析

通过调整舰船的航向，使右侧对准目标来向，此时天线方位甲板角约为90°，目标起飞前2 min生摇，当基带锁定、角误差稳定且天线的俯仰大地角高于3°时(为避免船摇时，俯仰甲板角运行到限位位置)，切自跟踪模式，实时记录俯仰甲板角及角误差变化情况。

事后分析船摇甲板角及角误差变化曲线如图5和图6所示。

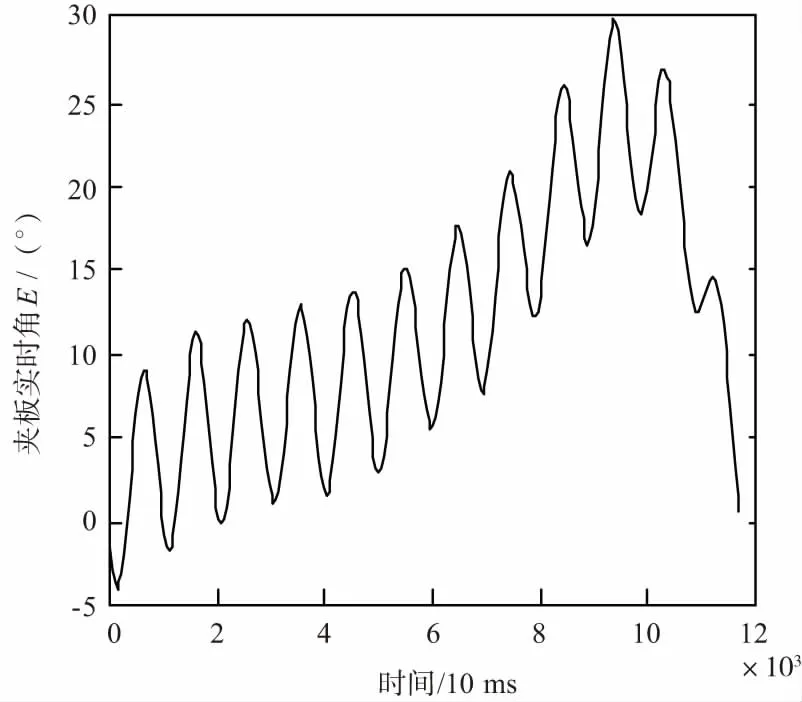
图5 跟踪环路甲板角测试曲线

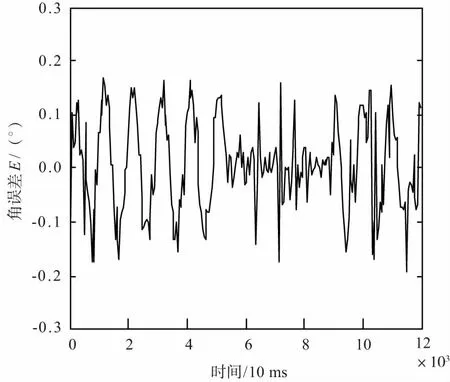
图6 跟踪环路角误差测试曲线

从中分别筛选出3个周期数据，如表1所示。在表1中，计算出相应周期下的船摇隔离度，统计得出跟踪精度为0.035 63°。船摇隔离度指标均优于40.0 dB设计指标。

表1 隔离度统计结果

周期数甲板角最大值/(°)角误差最大值/(°)隔离度/dB113.70.1340.5214.20.1340.8314.80.1341.1

3.3 数引环路测试数据分析

使天线指向船正右侧大地坐标系下某一固定点，此时天线方位甲板角为90°，为避免船摇时，俯仰甲板角运行到限位位置，该固定点对应的俯仰甲板角应具备一定高度[17]，现设为12°，然后生摇，记录俯仰甲板角及角误差变化情况。从中分别筛选出3个周期数据如表2所示。

表2 隔离度统计结果

表2中，计算出相应周期下的船摇隔离度，统计得出指向精度为0.012 21°。船摇隔离度指标均优于40.0 dB设计指标。

4 结束语

本文提出的伺服系统扰动隔离设计方法，在各种扰动作用下，系统输出动态变化小、恢复时间快、震荡次数少，能够有效提高舰载遥测装备在高海况下高动态目标的捕获跟踪能力[18]。对隔离度进行了充分试验验证，试验结果表明，该系统设计方法完全满足设计要求。为舰载遥测装备未来在远海陌生海域执行遥测测量任务提供了有效支撑。

[1] 王承瑶.陀螺稳定系统[M].北京:国防工业出版社,1985:56-57.

[2] 郎庆文,刘年宝,王统安.舰载跟踪雷达两轴稳定伺服系统的前馈补偿法[J].上海航天,1995(6)：3-8.

[3] 瞿元新.航天测量船测控通信设备船摇稳定技术[M].北京：国防工业出版社，2009.

[4] 张玉良，耿天文，刘永凯.动基座光电平台视轴自稳定控制系统设计[J].研究与开发，2015,34(9):38-42.

[5] 贾建辉,赵书阳,马纪军.船摇速度补偿算法在两轴天线伺服系统中的应用研究[J].遥测遥控,2017(2):62-63.

[6] HEEV S D.Airborne Satellite AntennaMou-nt and Tracking Systems[J].IEEE Africon，2004:287-289.

[7] 凡国龙,张录健,解旭东.高精度雷达天线自抗扰控制技术研究[J].无线电通信技术,2017,43(3):63-67.

[8] 李志坚,周朝猛,刘咏.隔离船摇补偿新方法探究[J].科学技术与工程,2009,9(19):5736-5738.

[9] 熊志广,张学飞.WCDMA终端控制干扰技术研究与实现[J].无线电通信技术,2017,43(3):91-94.

[10] 曹正才,金艳艳.舰载雷达伺服系统的复合控制[J].雷达与对抗,2004(1):51-52.

[11] 祁海禄,樊小平,詹盛武.某舰载伺服系统位置控制器设计与仿真研究[J].舰船电子工程,2010,30(2):64-67.

[12] 崔立廷.一种海面定向天线自动跟踪系统[J].无线电通信技术,2016,42(3):55-58.

[13] 鲍珊,姜素萍.舰载遥测设备伺服跟踪视轴稳定方法研究[J].飞行器测控学报,2009,28(3): 27-28.

[14] 杜璞玉,周勃,秦瑾.星载GNSS-R天线波束指向算法研究[J].无线电工程,2016,46(3):45-48.

[15] 武建亮,姜照昶,王文彦,等.航天测控动态数传数据模拟器的实现[J].无线电工程,2017,47(8):18-21.

[16] 李庆华.梯形加减速算法在伺服系统中的应用研究[J].无线电工程,2016,46(7):56-59.

[17] 李俊瑶,邹磊,杨卫平,等.测控系统伺服电机故障诊断方法研究[J].无线电工程,2016,46(1):80-82.

[18] 单福悦,凡嵩,岳建,等.基于多波束阵列天线的目标快速捕获方法[J].无线电工程,2016,46(4):60-62.