基于LCD与奇异值能量差分谱的齿轮故障诊断方法

丁 伟，陈可弟

（1.江苏信息职业技术学院 汽车工程学院，江苏 无锡 214153；2.中国矿业大学 机电工程学院，江苏 徐州 221116）

齿轮作为机械传动形式的基本组成元件，其运行中故障的发生直接影响到机械设备的运行状态以及工作效率[1]。因此，研究齿轮故障诊断在实际工程保障及提高工效方面都显得十分重要。

由于早期故障特征信息十分微弱，容易被干扰信息所淹没，如何有效实现齿轮故障特征信息提取成为非平稳信号处理过程中首要解决的问题。程军圣等在2012年提出的一种新的自适应信号时频分析算法[2]，该方法在分解速度和保真性方面优于经验模态分解，避免了包络误差等[3]。本文在此基础上提出一种基于SVR延拓处理的LCD改进算法，抑制分解过程中产生的端点效应。

SVD技术由于其具备的良好的非线性降噪能力，董文智等研究了基于EEMD和奇异值差分谱理论的轴承故障诊断方法来确定降噪阶次[4]，但是当信号中的特征信息较为微弱的时候，利用奇异值差分谱效果不佳。考虑到信号实际采集过程中受背景噪声干扰，本文研究利用奇异值能量差分谱降噪理论来确定逆SVD的重构阶次问题，进一步区分出信号中的有用成分和噪声成分。

因此，本文综合LCD算法与奇异值能量差分谱降噪理论各自的优点，对齿轮非平稳信号进行降噪预处理，提高信号的信噪比，从而有效地提取出信号的特征信息，进而完成齿轮诊断识别。

1 故障诊断关键技术

1.1 局部特征尺度分解

局部特征尺度分解属于自适应分解算法，以信号自身携带信息为基础，将信号分解为一组ISC分量之和[2]。任意两个ISC分量不直接关联，同时具有以下特点[5]：

(1)信号x(t)的任意两个相邻极值点的正负性不同；

(2)寻找到信号x(t)的所有极值点(τk,Xk)，其中k=1,2,…,M，M为所有极值点个数，其中选取任意相邻两个极大值(或极小值)点 (τk,Xk)和 (τk+2,Xk+2)的连线，在横坐标为τk+1的纵坐标表示为

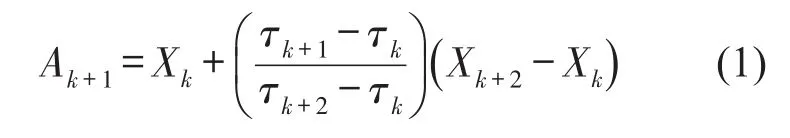
结合上述对ISC分量的基本定义，LCD对信号的分解流程如图1所示。

1.2 端点效应抑制方法

在自适应性分解过程中由于信号左右端点的极性无法判断，对于端点的处理就会产生误差，在分解的迭代过程中逐渐由两端向信号内部发散，造成分解结果出现失真。

基于SVR模型对时间序列向两端延拓处理构成新的时间序列，无需考虑端点极值问题[6]。因此，考虑基于SVR先对齿轮信号进行延拓处理，然后进行LCD分解，将得到的ISC分量去除延拓长度就得到延拓处理后的LCD分解结果，如此就能有效地提高分解可靠性和精确度。基于SVR的数据延拓大致步骤如下。

图1 LMD分解流程图

考虑到信号的复杂性，将齿轮样本非线性信号x投影到高维空间G中，实现线性回归对应处理。首先根据回归函数确定初始参数，选择合适的惩罚参数和精度参数；然后确定损失函数和经验风险值；最后选择适当的核函数，求解优化目标的最优解；构造出非线性回归模型[7]

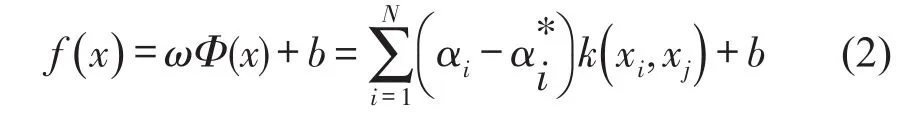
其中：通过b来调节阈值，ω为权重，为核函数，N为数据长度。

利用回归模型对时序信号向右延拓，然后翻转信号，再次向右延拓，翻转信号即得到左右延拓后的信号。

1.3 奇异值能量差分谱降噪理论

奇异值能量差分谱理论利用信号中有用成分与噪声成分在能量上的差异性来确定SVD降噪的重构阶次，然后利用SVD逆变换重构信号频谱，与LCD相结合，对分解得到的每一层ISC进行降噪预处理。降噪后信号中包含了主要特征信息，提高信号的信噪比。

时序信号X=[x(1),x(2),…,x(n)]，将一维信号重组成新的矩阵D，成为与之对应的Hankel矩阵[8]。

奇异谱是信号能量在奇异值上的表示。

其中：σi为信号行列变换得到的奇异值，q为奇异值数目，为了寻找到有用成分与噪声成分的分界，突出两者之间的差异，定义归一化处理后的奇异值能量差分谱为

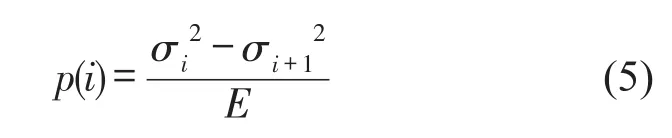
奇异值能量差分谱图表征了任意相邻两个奇异值之间能量差值曲线，谱图上最大值点表明这两个相邻奇异值对应的能量差最大，携带的特征信息差异性也就最大，通过这个能量突变点就能够有效地将信号中的有用成分与噪声成分区分开来，完成SVD降噪预处理。

2 实验装置及数据采集

验证算法有效性的实验数据在实验台上进行模拟采集，实验中齿轮振动信号的采集在载荷恒定的情况下进行，作为输出轴的电机转速设置为45 Hz，数采仪的采样频率设置为13 kHz，实验台如图2所示。

图2 实验台传感器布置图

为了有效测试诊断算法的有效性，模拟采集4种常见齿轮的振动信号进行分析判断，分别为正常、断齿、少齿以及磨损，实验采集到的齿轮振动信号时域图如图3所示。

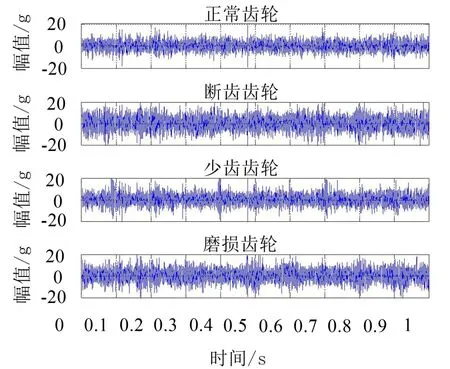
图3 4种状态下齿轮信号时域图

实验中采用加速度传感器，信号幅值单位用重力加速度g表示，取值为9.8ms2，对每种齿轮类型采集400组数据。

3 实验与分析

为了验证提出的基于改进LCD和奇异值能量差分谱的齿轮故障诊断算法的有效性，对实验中采集到的数据进行分析验证。考虑到不同数据验证过程的相似性，下面仅以齿轮磨损故障为例进行陈述。

对随机选择的一组齿轮磨损故障实验数据先进行SVR延拓然后进行LCD分解，分解结果如图4所示。

图4 齿轮磨损故障LCD分解结果

信号被分解后得到5个ISC分量和一个残余量R，为了验证算法改进前后的效果对比，同时将样本信号直接进行LCD分解，在时频域内分析两次实验得到的信号瞬时时频谱图(见图5)。

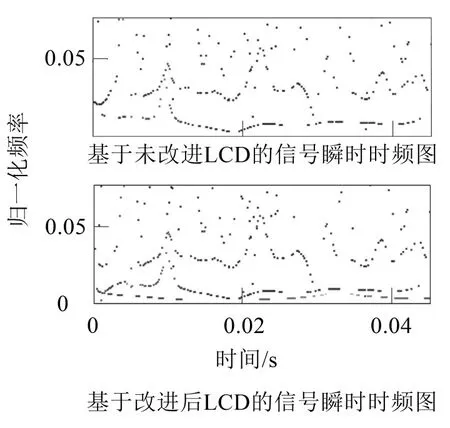
图5 LCD改进前后信号的瞬时时频谱图对比

可以看出，采用改进前LCD算法时，在低频率区端点处向上波动比较严重，而且信号有失真，效果并不理想；改进后，频谱两侧端点波动现象得到抑制，信息保存完整，对端点效应起到比较好的抑制作用，分解结果优于未改进算法分解结果，其分辨率也非常高，增加了信号预处理的精确度和有效性。

为了更进一步直观对比LCD改进前后的信号分解效果，下面通过仿真信号进行分析说明，s(t)=5 sin(200πt)+2 sin(80 πt)+sin(30 πt)，在实验中采样频率定为10 00 Hz，采样点数定为2 000。图6和图7分别为分别采用LCD改进前后算法时模拟信号的瞬时时频谱图，通过局部放大可以看出，在算法改进前，时频谱图中低频15 Hz的两端出现明显波动，分解结果受到干扰，算法改进后此现象明显得到有效抑制，分解结果更加精确，从仿真信号角度印证了LCD改进后带来的分解优越性。

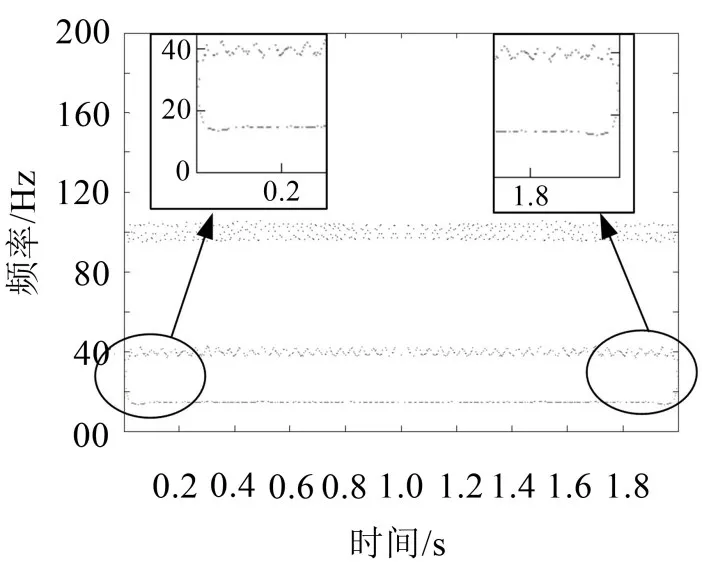
图6 LCD改进前模拟信号的瞬时时频谱图

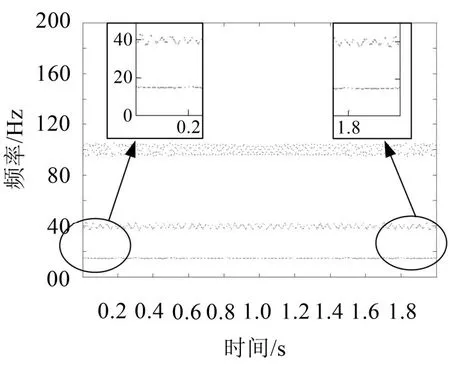
图7 LCD改进后模拟信号的瞬时时频谱图

文献[8]中通过数次实验发现，信号生成对应Hankel矩阵时，当数据长度N为偶数，设定行数m=N/2+1、列数n=N/2；数据长度N为奇数时，取列数m=(N+1)/2、行数n=(N+1)/2，这样构造的Hankel矩阵能取得较好的降噪效果。

下面对分解得到的各个ISC分量分别进行奇异值分解降噪，ISC1前50个点的奇异值能量差分谱如图8所示。

曲线上最大的极值点出现在第4个奇异值点上，按照奇异值能量差分谱降噪理论，选择前4个奇异值，后面奇异值直接赋值为0，进行逆SVD变换，对ISC分量进行降噪重构，降噪前后ISC1分量的时频对比图如图9所示。

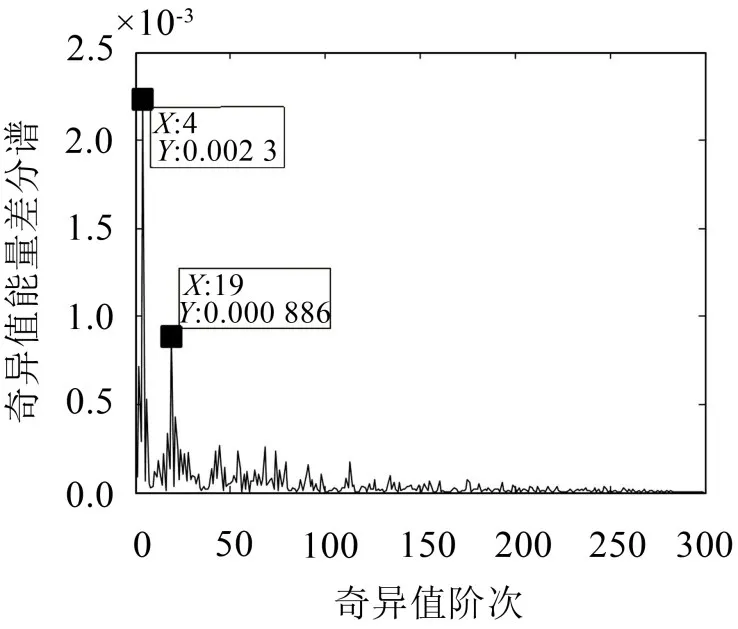
图8 ISC1奇异值能量差分谱图

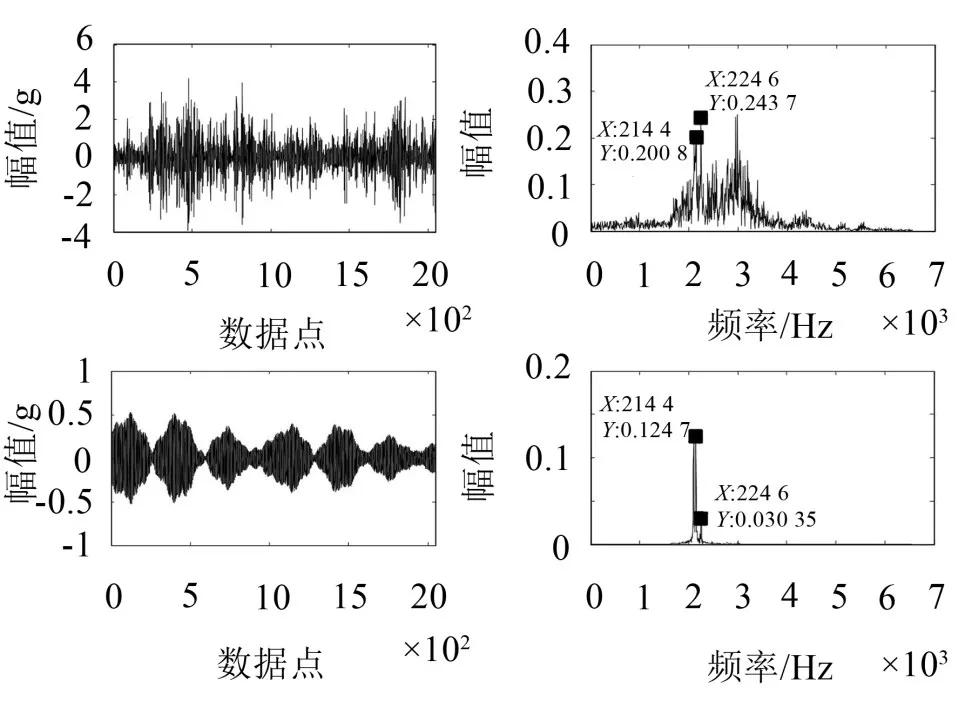
图9 降噪前后ISC1分量时频对比图

可以从频谱图中看到，降噪前ISC1分量频谱被噪声淹没，降噪后ISC1频谱中2 246 Hz对应输入轴转频的300倍频，2 144 Hz为啮合频率的13倍频，降噪后齿轮振动信号中的特征信息被很好提取出来。由上可知，逆SVD变换过程中，基于奇异值能量差分谱的降噪理论在信号降噪和保持信息完整性方面具有可行性和有效性。

对降噪重构后的4种齿轮状态信号提取特征信息，模糊熵具有良好的抗噪性和稳定性[9]，求得4种齿轮状态重构信号的各层ISC模糊熵值如表1所示（每种齿轮类型各取一个样本的模糊熵值）。

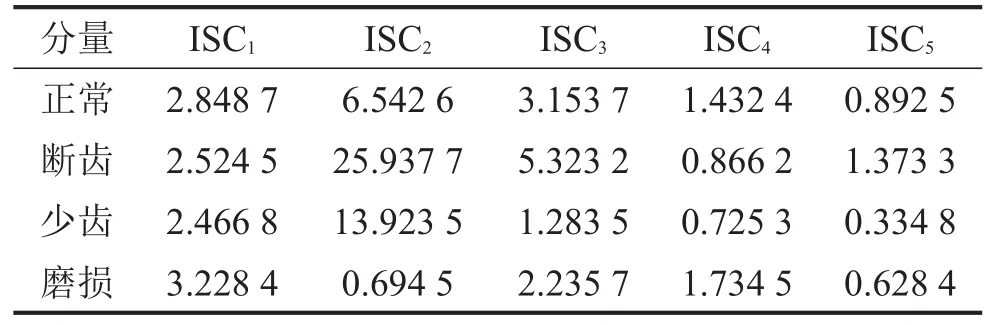
表1 各类状态齿轮振动信号ISC模糊熵

将对每种齿轮类型采集得到的随机300组数据进行以上操作提取出特征信息，用来训练SVM识别模型。剩下的各100组样本随机打散，输入到识别模型中进行诊断[10-11]，未对LCD进行改进的情况下4种齿轮类型的识别结果如表2所示，对LCD进行改进的情况下4种齿轮类型的识别结果如表3所示。在上述实验中，对LCD进行改进后，能有效提高齿轮故障诊断正确率，将4种齿轮类型的综合诊断识别率由88%提高到92%。

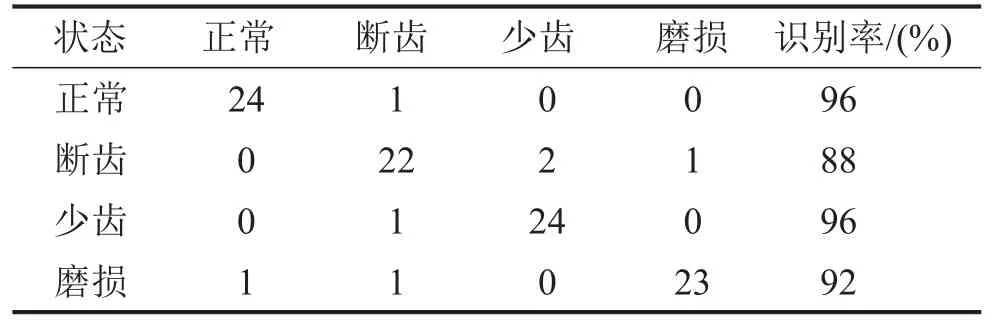
表2 LCD未改进时4种齿轮类型的识别结果

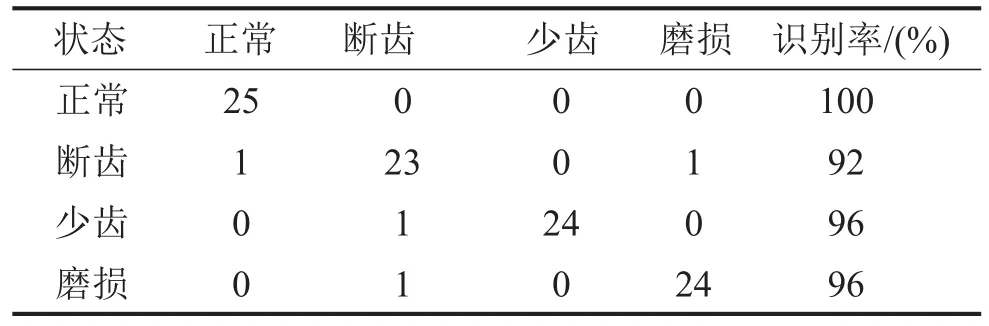
表3 LCD改进后4种齿轮类型的识别结果

4 结 语

实验结果表明，利用SVR延拓算法能有效抑制LCD分解中带来的端点效应，然后通过奇异值能量差分谱降噪理论对信号进行降噪预处理，滤除了信号中噪声成分的干扰，突出了携带的特性信息，提高了信号信噪比，最后利用训练好的识别模型SVM对提取的ISC模糊熵进行识别处理，能有效地诊断出齿轮多种故障类型，识别率达到92%以上，验证了该方法的有效性，同时也为齿轮故障诊断提供了理论支撑和实施途径。

参考文献：

[1]何正嘉，陈进，王太勇，等.机械故障诊断理论及应用[M].北京：高等教育出版社，2010.

[2]程军圣，杨怡，杨宇.局部特征尺度分解方法及其在齿轮故障诊断中的应用[J].机械工程学报，2012，48(9)：64-71.

[3]杨宇，曾鸣，程军圣.局部特征尺度分解方法及其分解能力研究[J].振动工程学报，2012，25(5)：602-609.

[4]董文智，张超.基于EEMD分解和奇异值差分谱理论的轴承故障诊断研究[J].振动工程学报，2011，34(5)：539-545.

[5]边兵兵.基于LCD降噪与LS-SVM的滚动轴承故障诊断方法[J].组合机床与自动化加工技术，2017(2)：119-122.

[6]王新，王乾，赵志科.基于SVR的经验模态分解端点延拓改进方法[J].计算机工程与应用，2014，50(9)：204-208.

[7]胡晓.强噪声背景下行星齿轮故障诊断研究[D].北京：中国矿业大学，2016.

[8]张文斌.奇异值能量差分谱在信号降噪中的应用[J].工矿自动化，2014，40(10)：25-28.

[9]CHEN WT,ZHUANG J,YU WX,et al.Measuring complexity using FuzzyEn,ApEn,and SampEn[J].Medical Engineering and Physics,2009,31(1):61-68.

[10]CORTES C,VAPNIK V.Support-vector networks[J].Machine Learning,1995,20(3):273-297.

[11]柳新民，刘冠军，邱静.基于HMM-SVM的故障诊断模型及应用[J].仪器仪表学报，2006，27(1)：45-48.