少片钢板弹簧片间动摩擦系数计算方法研究

李雪梅，陈综艺，刘夫云，汤长波，陈厚锦

（桂林电子科技大学 机电工程学院，广西 桂林，541004）

钢板弹簧的片间动摩擦特性是钢板弹簧阻尼特性研究的重点和热点之一。目前，少片钢板弹簧设计计算方法中关于板簧摩擦系数的研究很少，而板簧片间摩擦系数对钢板弹簧动态特性有着重要影响，国内外研究人员广泛采用CAE法对此展开研究。国外研究钢板弹簧的性能主要基于有限元数值计算方法[1-2]。樊翠连等研究了接触摩擦对等截面钢板弹簧的力学性能影响[3]；叶南海等研究了不同摩擦系数的变截面钢板弹簧性能[4]；唐应时等考虑接触摩擦计算了多片钢板弹簧悬架预应力[5-6]。这些研究大多是针对等截面钢板弹簧，且仅考虑了板簧片间的干摩擦，一般设定摩擦系数为定值，而针对少片钢板弹簧进行性能研究时很少有人提出板簧片间动摩擦系数的计算方法。

本文以某载货汽车后悬架少片钢板弹簧为对象，考虑实际工况下板簧的大变形，首先根据钢板的变形动力学特性，分析出钢板弹簧片间的动、静摩擦系数关系，接着建立少片钢板弹簧静摩擦系数计算模型，最后推导出少片钢板弹簧片间动摩擦系数计算方法，研究了影响少片钢板弹簧动摩擦系数非线性因素的变化规律。

1 少片钢板弹簧片间动摩擦系数计算模型

汽车行驶过程中，钢板弹簧各簧片之间相互滑动，导致了摩擦现象的存在。车辆上的少片钢板弹簧只有端部和中部相接触，少片板簧的中部被U型螺栓所固定，在实际工况下少片钢板弹簧中部产生的摩擦很小，对少片板簧性能带来的影响可以忽略。少片钢板弹簧端部垫块嵌入在少片簧副片簧的卡槽里，与副片簧一起运动。端部垫块与副片簧之间没有摩擦，摩擦只存在于垫块上表面与主片簧的下表面之间，所以少片钢板弹簧的片间摩擦属于外摩擦。本文通过外摩擦机理研究，建立了少片钢板弹簧片间动摩擦系数的计算模型。

1.1 钢板弹簧的变形运动学分析

假设少片板簧在垂直载荷作用下，簧片各处所受的应力接近相等，当板簧受到压力变形时，每个簧片的变形规律行为一致。因此，板簧的变形规律可转化为主片簧的变形规律，所以主片簧全长的形状近似地看成是一个圆弧，并且它的半径随着载荷而变化。坐标原点取固定端卷耳中心处，分析当板簧弧高y发生变化时，主片簧中点P的水平坐标x的变化规律。图1所示为一副水平布置的对称板簧变形的示意图。

设板簧的卷耳半径为r，板簧长度的一半为l，曲率半径为R，张角为θ。由几何关系有

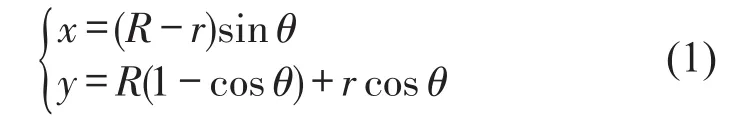
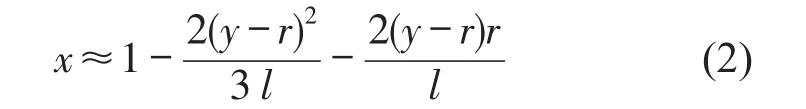
式中r为主片簧卷耳中心线半径；x为P点相对O点的水平位移；y为P点相对O点的垂直位移；l为板簧的半长度；R为曲率半径；θ为张角。

1.2 板簧片间动摩擦系数计算模型

根据文献[8]可知：对于一般干摩擦而言，它的摩擦系数μ随着滑动速度的增加而减少，即摩擦系数与滑动摩擦速度的关系曲线具有负斜率。

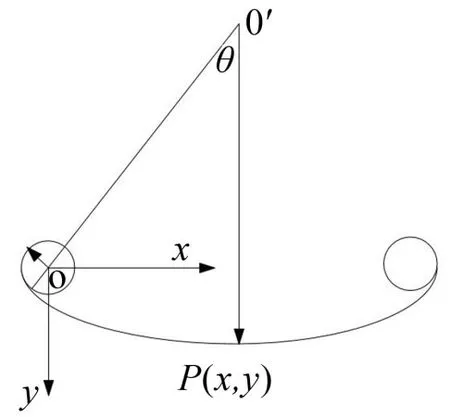
图1 板簧变形运动学分析

式中μ0为静摩擦系数；ẋ为板簧相对变形速度；β为摩擦系数随滑动速度变化曲线的斜率角度。

假设板簧的垂直相对位移为y=Asinωt+A0，则

其中A为振幅，A0为板簧满载弧高。

所以对式（2）求导可以得到

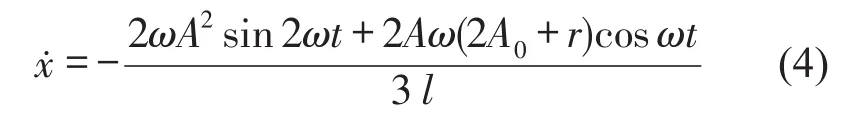
代入式（3）中，板簧的片间动摩擦系数μ可表示为

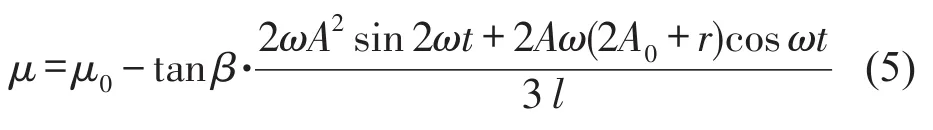
2 基于摩擦功的板簧片间静摩擦系数计算方法

本文通过摩擦功分析方法，建立钢板弹簧的力学计算模型，得到一种在加载振幅和频率较小的工况下板簧片间摩擦力做功的计算公式；根据能量转换关系，推导出板簧在静载压缩下摩擦功的计算公式。根据摩擦功相等原理，得到板簧的静摩擦系数。

2.1 基于力学法的板簧片间摩擦功计算模型

2.1.1 板簧片间相对变形的分析计算

假设预载力为P，钢板弹簧主片长为L1，副片长为L2，中部片厚为s，振幅为±A，图2为主片在振幅为-A和A时的状态示意图。

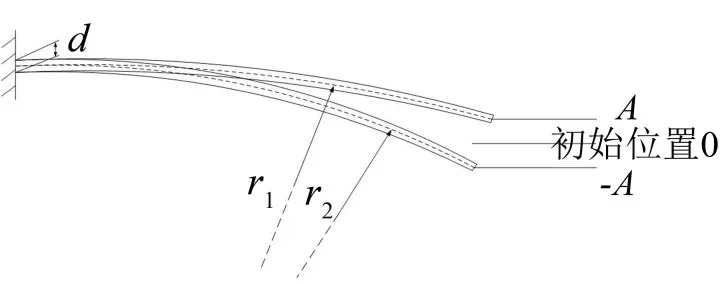
图2 主片在振幅为-A和A时的状态示意图

振幅在-A和A时，主片簧的曲率半径分别为r1、r2，由于板簧端部片间装有垫块，可视主片簧与副片簧的中性面到中部和端部的距离相等，均为板厚s，则副片簧的曲率半径分别为r1+s，r2+s。钢板弹簧在动态力作用下，振幅从-A到A时，钢板弹簧曲率半径变大，各叶片下表面被压缩，上表面被拉伸，其具体滑移量为主片簧下表面的压缩量与副片簧上表面的拉伸量之和，其上下表面长度尺寸随着曲率的变化而变化。根据弯曲梁理论，对于对称截面，对称面就是中性面。r1、r2、r1+s，r2+s即表示中性面的曲率半径，中性面的长度不变，即为钢板弹簧片长，则主片簧在振幅从-A到A的过程中其下表面的压缩量为

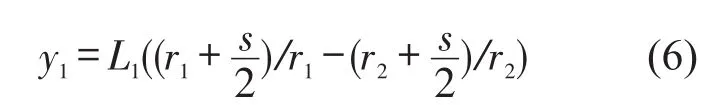
副片簧在振幅从-A到A的过程中其上表面的拉伸量为

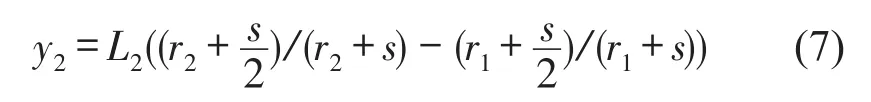
则一端总的滑移量为

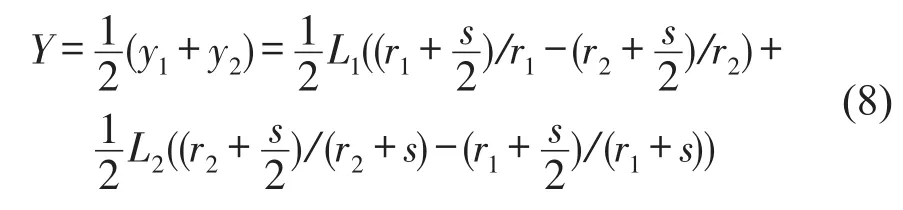
2.1.2 板簧片间正应力的分析计算

板簧片间应力包括正应力和切应力，由于摩擦产生的切应力较小，因此本文忽略切应力对总应力的影响。因为钢板弹簧的片长远大于弧高，正应力方向与预紧力方向夹角较小，所以可将钢板弹簧两端部的片间正应力的代数和近似为预紧力Fy。中心螺栓拧紧产生的预紧力Fy使得副片簧曲率变小的同时，主片簧曲率变大，在预紧力的作用下主片簧和副片簧的中部相接触。由于主片簧和副片簧具有相同的刚度K静/2，其间作用力为一对作用力与反作用力，因此两片簧预紧过程中的挠度相等，方向相反，假设主片簧由于预紧力产生的变形量为-∆x，则副片簧为∆x。螺栓预紧后，对其进行预载力加载，因为两片簧端部和中部紧密贴合，在预载力为P时，主片簧和副片簧的变形量相等，设其为x，则主片簧和副片簧的挠度分别为 -(∆x+x)和(∆x+x)，主片簧和副片簧自由状态下弧高分别为a和b。则有

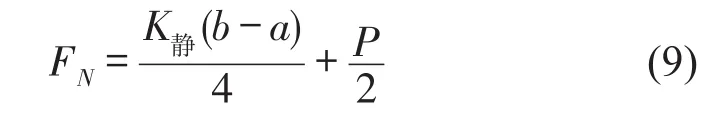
式中：FN是振幅为0时钢板弹簧两端部的片间正应力之和。动态工况下正应力是一个变力，随振幅的改变而改变，但变化较小，且其均值近似等于振幅为0时的正应力[9]，本文将这个变力等效为恒力FN。

2.1.3 计算摩擦力做的功

板簧接触处的摩擦系数为静摩擦系数μ0，一个周期内两端部片间滑移量均为2Y，端部片间正应力均为FN/2，则一个周期内摩擦力所做的功Ws为

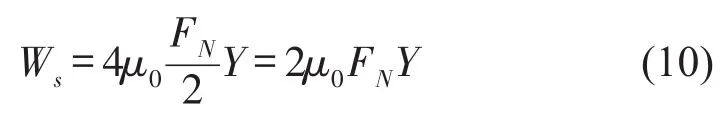
2.2 基于能量法的板簧片间摩擦力做功计算模型

钢板弹簧在静载压缩时会发生一定的变形，静载荷对钢板弹簧做的功一部分用于移动簧载质量，包括簧载质量的动能和势能，还有一部分则用来克服摩擦力做功。根据能量守恒定律，少片板簧静载压缩下的摩擦功计算方法如下

式中：Ef为少片簧摩擦力做功的理论值；E总为静载荷对板簧总成所做的外力功；UL为板簧质量的势能；Ek为板簧质量的动能。

在实际工况中，钢板弹簧静刚度的变化非常小，可视为恒定。外载荷从0增加到P，外力是线性变化的，将外载荷P对板簧所做外力功等效为1/2P的外力对板簧所做恒力功。其中X是板簧在外载荷P作用下产生的变形量。

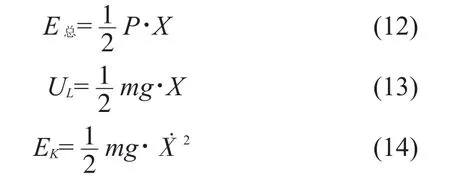
通过弯曲梁理论可知，板簧在较小激励工况下片间摩擦行为和静载压缩下片间摩擦行为基本一致[10]。根据摩擦功的相等关系，得到式(15)、式(16)。

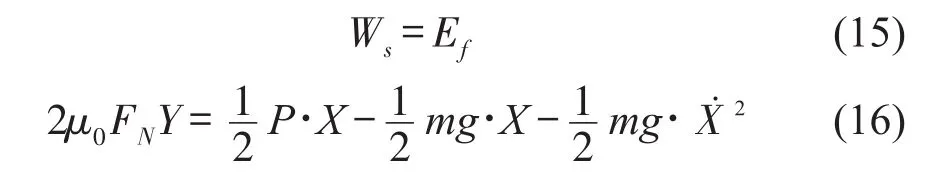
由此可以得到板簧的静摩擦系数如下

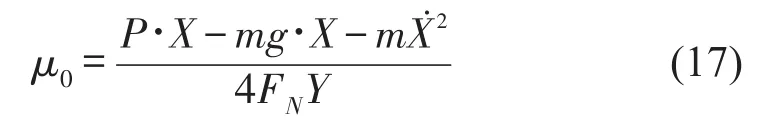
最后，根据式(5)所示板簧间动、静摩擦系数的关系，推导出少片钢板弹簧动摩擦系数为

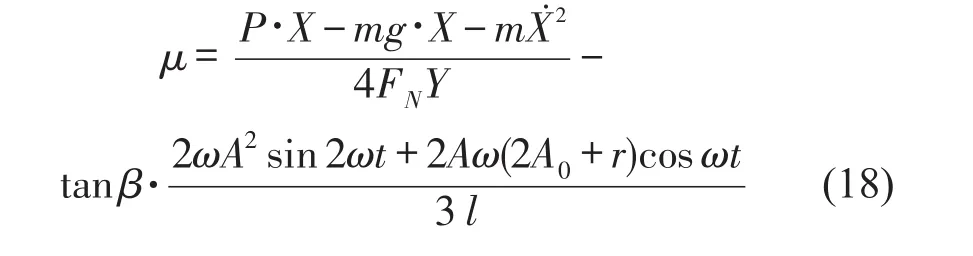
3 台架试验与应用计算

3.1 摩擦功的试验验证

图3所示为钢板弹簧台架试验，采用PWS-20动静态试验机对钢板弹簧进行加载。图4所示是台架试验中分析得到的少片钢板弹簧的载荷-变形特性线，加载曲线和卸载曲线之所以存在差距，是因为簧片间存在摩擦[11]。计算得出载荷差值曲线与坐标轴所围的面积，就是在不同的外载荷下，由台架试验得到的静态摩擦功大小Es。

图3 钢板弹簧台架试验

通过图4中载荷差值曲线与坐标轴所围的面积得到静态摩擦功的试验结果Es，采用式（10）计算板簧在静态工况下不同载荷下摩擦功的理论值Ws，运用能量法公式（11）求得板簧在静载压缩时不同载荷作用下的摩擦功理论值Ef。

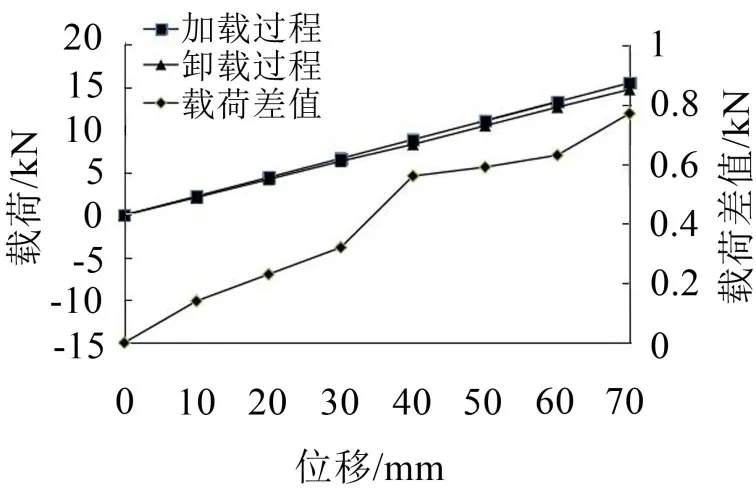
图4 钢板弹簧的载荷-变形特性曲线

表1为静态工况下不同载荷作用时的Wf与Ws及其相对误差。表2为静载压缩时不同载荷作用下的Wf与Es及其相对误差。

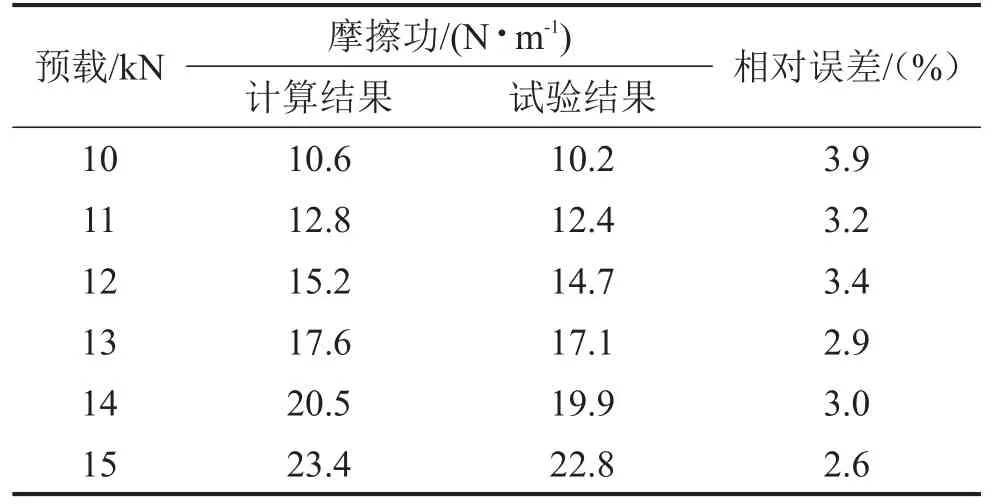
表1 静态工况下不同载荷下的Wf与Ws及其相对误差

表1中Ws与Wf相对误差小于5%，且Ws略大于Wf。误差产生的原因是由于钢板弹簧在加载作用过程中，其片间的摩擦行为部分转换为滑动摩擦，摩擦系数降低，从而摩擦损耗的能量减少；其相对误差随着预载的增大呈现减小的趋势，这是由于在预载力较大时，片间正应力增大，摩擦行为主要表现为静摩擦，摩擦系数增大，因而与理论值偏差较小。由表2可以看出，理论计算与实验测得的摩擦功的相对误差在合理范围内，从解决工程实际问题的角度出发，具有一定的参考价值。上述实验证明，板簧在静态工况下和静载压缩下摩擦力做功的理论值与试验测得的摩擦功的值相对误差在合理范围内。

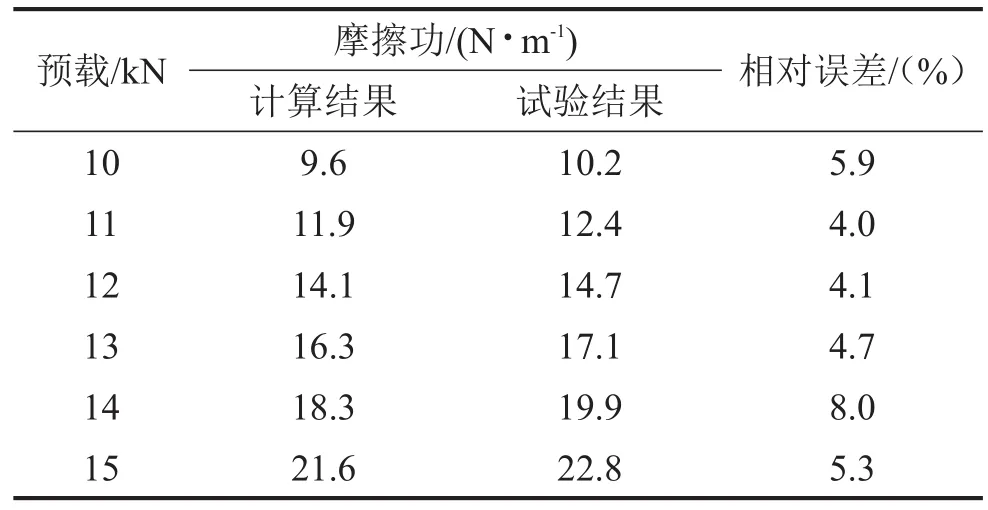
表2 静载压缩下不同载荷下的Wf与Es及其相对误差

3.2 板簧片间摩擦系数计算模型实例分析

本文所用的钢板弹簧为某汽车企业提供的型号为2912030的二片钢板弹簧，表3为该板簧叶片自由状态下的结构参数。

采用PWS-20动静态试验机可以实现钢板弹簧静态压缩试验和动态振动试验。本文提出的摩擦系数计算方法可以看成两部分：静摩擦系数的计算模型和动摩擦系数的计算模型。通过上述模型的计算方法，将少片钢板弹簧的结构参数、试验条件参数代入式（17）可以得到板簧的静摩擦系数，代入式（5）可以分析试验工况下振幅、频率和斜率角度对板簧动摩擦系数的影响的变化规律。以实际板簧型号2912030为例，得到板簧静摩擦系数的计算结果图，见图5。从图5可以看出：静摩擦系数的变化规律与载荷、振幅有关。静摩擦系数的大小随载荷增大而增大，随振幅的增大而减小。

在实际工况下板簧的相对位移变形量符合如下形式：y=Asin(2πft)+A0，上述的数学模型中，对影响板簧动摩擦系数的因素进行分析。通过本文的动摩擦系数计算模型可以看出，影响动摩擦系数的主要因素是预载荷、加载频率、振幅。

而实验中对板簧施加的预载荷是影响板簧静摩擦系数的主要因素。

本文讨论的重点是板簧的施加振幅、加载频率和斜率角度对板簧动摩擦系数的变化规律，见图6。可以得出结论：板簧动摩擦系数随振幅增大而减小，随频率增大而增大，随斜率角度增大而增大。并且可以看出振幅对板簧动摩擦系数的大小影响显著，频率和斜率角度影响不明显。

表3 板簧叶片自由状态下的结构参数

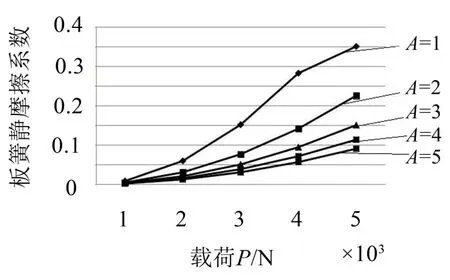
图5 板簧型号2912030静摩擦系数的计算结果图

4 结语

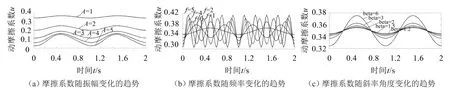
图6 影响板簧摩擦系数因素的计算结果图

（1）进行钢板弹簧的变形运动学分析，得到动、静摩擦系数之间的关系。建立了少片钢板弹簧静摩擦系数计算模型，根据能量转换守恒原理，基于力学法和能量法提出了板簧片间静摩擦系数计算方法。文中以某载货车前悬钢板弹簧为算例通过台架试验验证了该算法的准确性。

（2）推导出一种少片钢板弹簧片间动摩擦系数的计算方法，通过计算得到钢板弹簧片间动摩擦系数的变化规律：少片板簧片间摩擦系数随振幅增大而减小，随频率增大而增大，随斜率角度增大而增大。可以看出，根据本文提出的计算方法得到的计算值与实际工况值在0～0.2之间较为吻合，且动摩擦系数计算值的正弦结果图和板簧实际工况下的值基本一致。利用本文所提出的方法，可以在样品开发设计阶段预测钢板弹簧在动态工况下的摩擦系数，便于对钢板弹簧进行正向设计。

参考文献：

[1]周水庭，黄红武，付建朝，等.基于接触摩擦的变截面钢板弹簧悬架性能分析[J].湖南大学学报(自然科学版)，2013，40(5)：44-48.

[2]KRISHAN K.A finite element approach for analysis of a multi leaf spring using CAE tools[J].Research Journal of Recent Scsenes,2012,1（2）:92-96

[3]樊翠连，李舜酩，张袁元.钢板弹簧刚度特性及接触摩擦的非线性有限元分析[J].噪声与振动控制，2012，32(3)：16-20.

[4]叶南海，王利，闫彩伟，等.不同摩擦系数的少片变截面钢板弹簧性能分析[J].湖南大学学报(自然科学版)，2015(8)：29-33.

[5]唐应时，陈明媚，潘佳炜，等.基于接触摩擦的多片式钢板弹簧悬架预应力的计算[J].湖南大学学报(自然科学版)，2009，36(4)：29-33.

[6]唐应时，柴天，和进军，等.基于接触摩擦的少片变截面钢板弹簧的刚度分析[J].中南大学学报(自然科学版)，2009，40(3)：694-698.

[7]郭孔辉.板簧变形运动学分析及其应用[J].汽车工程，1990(2)：7-15.

[8]孙中辉，王景晟.基于钢板弹簧非线性的整车平顺性分析[C]//2009中国汽车工程学会年会.北京，2009.

[9]MAEGAWA S,ITOIGAWA F,NAKAMURA T.Effects of stress distribution at the contact interface on static friction force:numerical simulation and model experiment[J].Tribology Letters,2016,62(2):15.

[10]孙训方.材料力学[M].北京：高等教育出版社，2009.

[11]张智，卢剑伟，陈渊锋，等.不同摩擦系数的钢板弹簧动态特性分析[J].汽车工程学报，2013，3(2)：94-99.