一种基于压电堆执行器的柔性结构滞后补偿PID控制

赖俊杰，浮 洁，李沛东，白俊峰，余 淼

（重庆大学 光电工程学院光电技术及系统教育部重点实验室，重庆 400044）

实际工程中，房屋、桥梁、航天器连接构件等柔性结构对振动极其敏感[1-2]。振动会造成系统结构损伤甚至破坏，因此振动控制非常重要。传统被动隔振（橡胶或液压隔振器）结构简单，对高频振动衰减效果明显但自适应性差。因此对具有多频激励的柔性结构振动抑制效果不佳。压电陶瓷执行器由于响应速度快、输出力大等优点，在结构振动控制研究中受到极大关注。与压电片相比，压电堆具有更大的输出力，将其作为执行器可以很好地实现柔性结构的振动抑制[3]。

执行器结构、安装位置和控制系统的硬件组成等一旦确定，振动抑制效果与控制算法有直接的关系。根据算法与控制对象模型的相关性分为依赖于模型的算法和不依赖于模型的算法。依赖于模型的算法诸如LQR、H∞等[4-6]可求出精确的控制参数，但要求对象模型精确已知。不依赖于模型的算法包括PID、模糊控制[7-8]等与对象模型无关。其中PID控制器由于结构简单，易于实现，被广泛应用在机械，自动化，电力能源等领域[9]。

柔性结构控制系统中存在较大的相位滞后，主要影响因素有：

(1)为消除控制系统中存在的噪声干扰（硬件系统数模输出端存在高频噪声、信号发生器和功率放大器的输出存在纹波失真、信号调理器中存在非线性失真、试验环境中人员走动、空调压缩机运行与建筑物摆动、信号传输线屏蔽效果不佳等），需引入带通滤波器，从而使控制信号产生相位偏移。

（2）反馈点与控制点位置不同，引起振动信号与控制信号之间的相位滞后，其为控制系统产生滞后的主要因素。

（3）柔性结构与压电堆等机械系统的响应也存在滞后。相位滞后会影响振动控制效果，甚至放大振动。而常规的PID控制器难以解决该问题。现有针对相位滞后的补偿方法如Dahllin算法，Smith预估算法[10-11]，内模控制算法（IMC）[12-13]等均需通过对象数学模型预估来消除相位滞后，对于结构复杂的柔性结构来说很难建立其精确的数学模型。

此外，柔性结构系统在实际应用中的激励常为多频振动，且滞后补偿大小与激励频率有关。因此，单一的滞后补偿PID控制器难以达到满意的控制效果。本文提出采用分频滞后补偿PID控制方法，即通过带通滤波器组对误差信号进行窄带滤波从而实现信号的分频[14]。

基于以上分析，本文针对具有相位滞后的柔性结构多频振动问题，提出相位滞后补偿PID控制方法，通过理论分析和实验辨识出激励频率和相位滞后补偿值间函数关系。并针对多频率振动问题进行分频控制，实现多频振动的抑制。所提方法无需建立柔性结构系统的精确模型且易于实现。

1 柔性梁结构模态仿真与试验

基于压电执行器的柔性结构系统如图1所示，系统由简支梁、压电堆和基础三部分组成。其中简支梁（304不锈钢材质、长600 mm、宽50 mm、厚2 mm）模拟柔性结构，压电执行器采用40VS12型机械封装式压电陶瓷。为了保证压电执行器在垂直方向工作，通过聚氯乙烯螺杆将其安装在梁中央处（图1中位置2处）。

由于压电执行器的放置会使简支梁约束增加从而改变系统振动特性。为获得简支梁振动控制系统精确的振动特性（振型和共振频率），需对安装有压电执行器的柔性结构系统进行模态分析。本节将通过ANSYS仿真和扫频试验进行分析和验证。

1.1 柔性梁结构模态仿真

通过ANYSY/Workbench对简支梁主动控制系统进行建模，得到如图2所示的振型图。

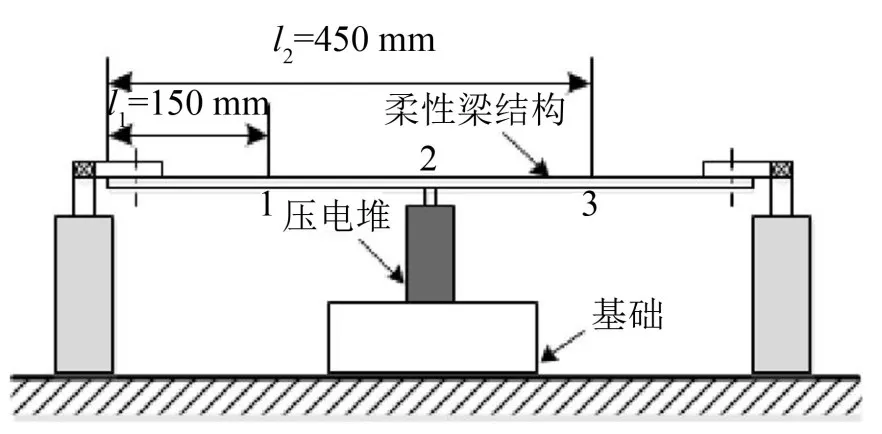
图1 压电堆主动振动控制系统

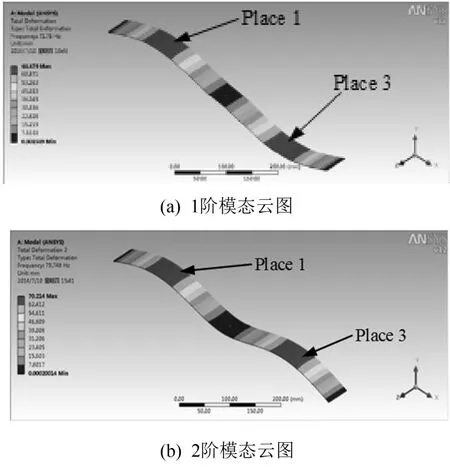
图2 柔性梁控制系统

由图可知梁的位置1、3处均为1、2阶模态共振峰位置点，振动频率分别为71.76 Hz和83.45 Hz，且2阶模态振幅最大，最大值约为70 mm。由于3阶及以上模态振型峰值较小，因此只考虑柔性梁前2阶模态。

1.2 简支梁模态试验

为验证仿真模态分析的正确性，搭建如图3所示的柔性梁结构振动特性测试系统。半实物仿真平台dSPACE AutoBox产生扫频信号通过功率放大器驱动激振器激振柔性梁系统。加速度传感器获取柔性梁振动加速度经信号调理器进入半实物仿真平台中，并通过上位机记录分析数据。根据理论模态分析结果确定扫频范围为20 Hz～200 Hz，扫频结果如图4所示。

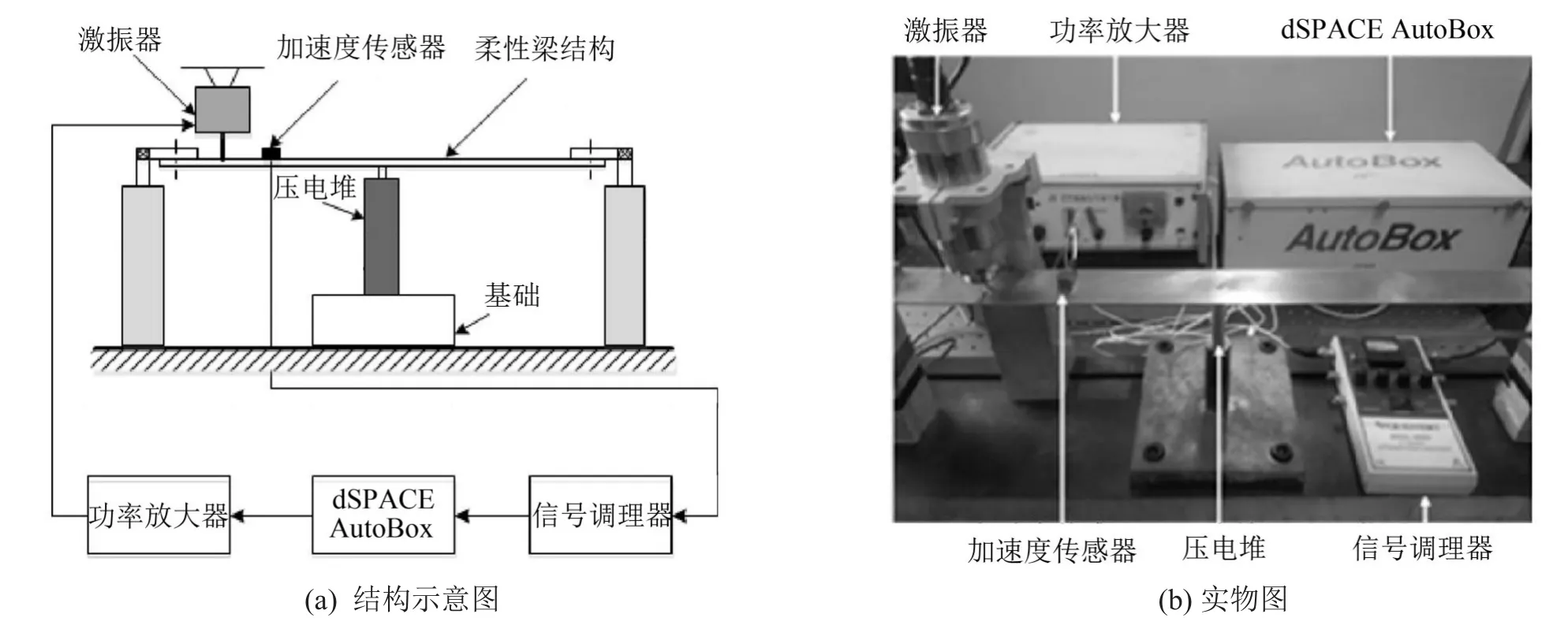
图3 柔性梁模态分析实验系统

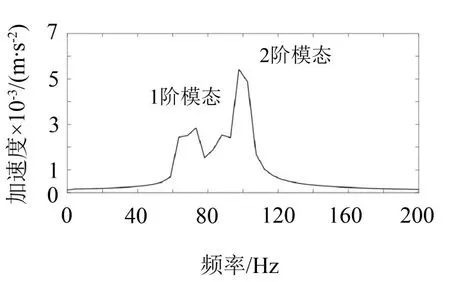
图4 柔性梁扫频结果频谱分析

由图4可知，1阶、2阶共振频率分别为70 Hz和95 Hz，且在2阶共振频率处梁振动幅度最大，为其主导模态。实验结果与理论分析结果相近，验证了理论分析的正确性。

2 具有滞后补偿的分频PID控制器设计

针对柔性结构中存在的延时和多频激励问题，设计如图5所示的分频滞后补偿PID控制器。多频加速度误差信号经过不同带通滤波器后被分离为多路单频加速度信号，然后对单频信号分别进行相位滞后补偿，最后基于线性叠加原理将补偿后的信号混叠经PID控制器中进行控制。

2.1 PID控制器

PID控制器的原理图如图5所示，其输入为简支梁位置3处的加速度误差，输出为压电堆的驱动电压。由误差比例部分kpe(t)、积分部分ki∫e(t)dt和微分部分组成

式中：e(t)=0-a(t)=-a(t)为系统加速度误差信号，a(t)为简支梁位置3处的加速度响应信号，u(t)为控制器的输出电压，kp、ki和kd分别为比例系数、积分系数和微分系数。

PID控制器结构简单，无需对柔性梁结构进行精确建模，但其鲁棒性较差，对系统内存在的噪声和相位差十分敏感，因此，将结合滤波和相位补偿方法进行噪声和延时控制。

2.2 滞后补偿理论

柔性结构控制系统中存在的总延时Φ(f)由带通滤波器产生的相位偏移Φ1(f) 、反馈点（图1（a）中1）与控制点（图1（a）中2）位置不同所引起振动信号与控制信号之间产生的相位滞后Φ2(f)、结构本身响应延时Φ3(f)组成，即Φ(f)=Φ1(f)+Φ2(f)+Φ3(f)，其中f为激振信号频率。

本文采用图3所示的测试系统获得系统相位差。dSPACE中分别产生70 Hz、80 Hz、95 Hz、125 Hz单频正弦信号，信号通过压电驱动器放大以驱动压电堆振动从而激振柔性梁结构。安装在梁1/4处的加速度传感器测得柔性梁振动加速度信号，并通过调理器将其转换为电信号。将加速度信号上传至上位机，在上位机中通过比较单频正弦激振信号与加速度信号可得控制系统对不同激振频率信号产生的滞后相位Φ(f)。测试结果如表1所示。

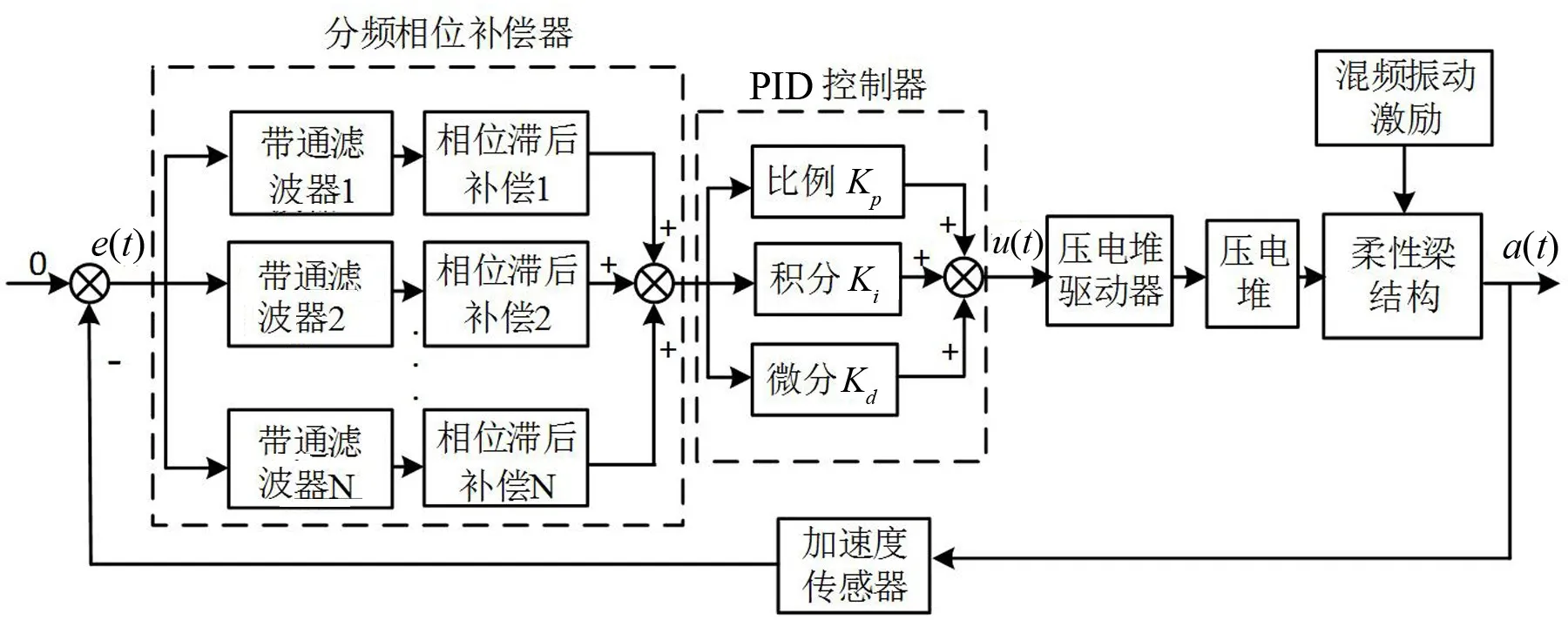
图5 柔性结构分频相位补偿PID控制系统

表1 滞后相位角

根据表1中不同激励信号频率下的相位差值，结合各频率信号周期可拟合出滞后补偿量与信号频率之间的函数关系见式（2）。

其中：n为单频激励加速度信号周期，n∈N。n的大小不影响滞后补偿后系统控制效果。计算出各频率点的滞后补偿值如表2所示。

表2 滞后补偿时间

为便于补偿控制系统中的相位差，可将其随激振频率的变化关系转换为滞后时间和激励频率的关系。根据表2对激励频率与滞后补偿时间进行线性拟合，拟合结果如图6所示。由图6可得拟合公式

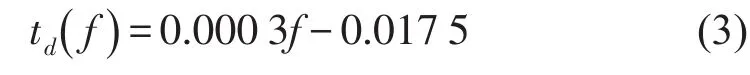
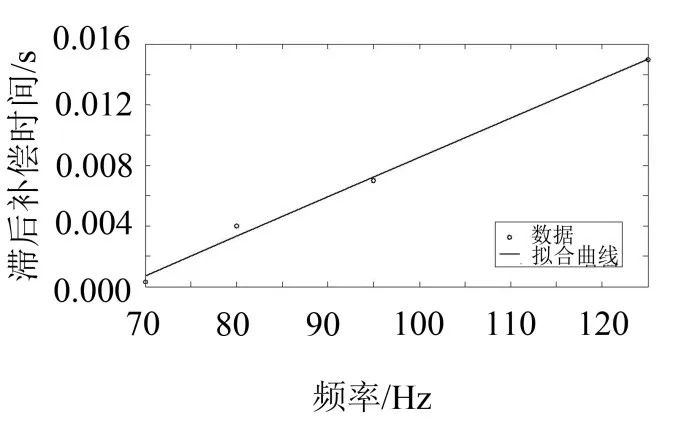
图6 滞后补偿时间与激励频率间函数关系

其中td(f)为滞后补偿时间。根据上式可求出各激励频率下系统需补偿的滞后时间。

不同的激励频率对应着不同的相位补偿器。多频振动激励内存在多种频率成分，若只采用一种相位补偿器，某些频率成分的振动可能会被放大，甚至导致系统振荡。为此本文基于线性系统的叠加原理设计了如图5所示的分频相位补偿PID控制器。

2.3 带通滤波的设计

带通滤波器在系统中有两个作用：其一，滤除信号传输过程中的噪声干扰；其二，由于加速度信号滞后与激励频率相关，因此可通过带通滤波器分离信号进行滞后补偿。带通滤波器会导致加速度信号相位失真，本文选取有限冲击响应（FIR）滤波器保证滞后与信号频率间的线性关系。为减少实时控制系统中振动加速度信号幅值失真对控制效果的影响，带通滤波器通带区内采用波动幅度为0.3 dB的等纹波设计。考虑滞后补偿的准确性和硬件实现条件，所设计的窄带带通滤波器参数如表3所示。

表3 各带通滤波器参数设置

3 实验结果与分析

由于实际应用中柔性结构系统常发生多频振动，因此主要考虑双频和三频激励振动情况。激励为70 Hz(1阶共振频率)、80 Hz、95 Hz(2阶共振频率)、125 Hz等频率成分的组合，控制实验系统如图7所示。

图7 具有分频相位补偿的PID控制实验系统

考虑到硬件条件的限制，试验中滤波器采样频率为1 800 Hz，滞后补偿在MATLAB/Simulink软件中通过“Transport Delay”时域延时模块实现，并将加速度作为试验振动衰减评定参数。

3.1 双频激励振动控制

双频激励条件（70 Hz+80 Hz、70 Hz+95 Hz、80 Hz+95 Hz、80 Hz+125 Hz）下确定PID控制器参数如表4所示，此参数为70 Hz+95 Hz条件下最优参数。具有滞后补偿的PID控制器控制效果及压电堆控制电压见图8－图9，双频混合激励在常规PID控制器与分频滞后补偿PID控制器控制前后加速度均方根值及衰减如表5所示。

由振动控制前后加速度频谱图和表5可知分频滞后补偿后柔性梁结构振动衰减相较常规PID控制效果明显，特别在1、2阶共振频率处最大衰减均可达40%以上。

3.2 三频激励振动控制

本节研究三频激励条件（70 Hz+80 Hz+95 Hz、70 Hz+80 Hz+125 Hz）下控制器的控制效果、控制器参数如表6所示，此参数为70 Hz+80 Hz+95 Hz条件下最优参数。分频滞后补偿PID控制器的控制效果及压电堆控制电压如图10所示，各三频混合激励的PID控制器参数如表6所示，三频混合激励在常规PID控制器与分频滞后补偿PID控制器控制前后加速度均方根值及衰减如表7所示。因此经过相位补偿后的PID分频控制器可有效衰减多频混叠振动，特别是使包含共振频率的振动加速度衰减最高达40%以上。

4 结语

针对具有多频激励和延时的柔性结构振动问题，提出分频相位补偿PID控制方法。通过理论模态分析和试验模态分析确定柔性梁的1阶模态频率（70 Hz）和2阶主导模态频率（95 Hz）。通过实验测试及数据拟合得出各频率点滞后补偿与激励频率的函数关系，设计了分频滞后补偿PID控制器。搭建试验系统并与常规PID控制器控制效果对比，验证了多频振动条件下所设计控制器的有效性，其中加速度均方根最大衰减可达45%，证明所设计控制器能较好抑制柔性梁结构的振动。10-19.

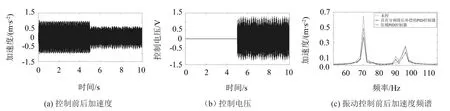
图8 70 Hz+95 Hz双频激励控制效果

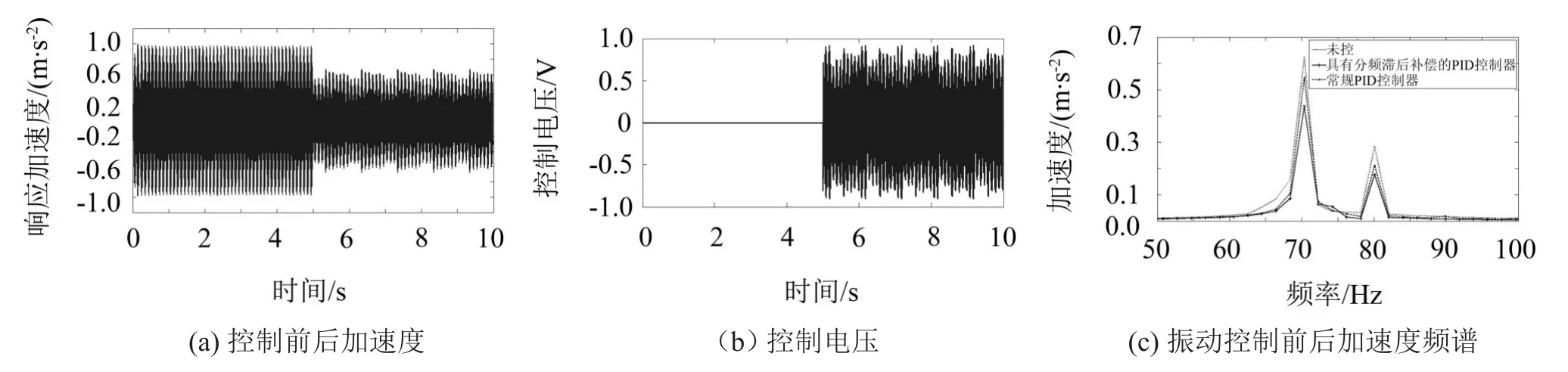
图9 70 Hz+80 Hz双频激励控制效果

表5 双频激励条件下分频相位补偿前后加速度均方值及衰减率对比

表6 三频激励条件下PID控制器参数

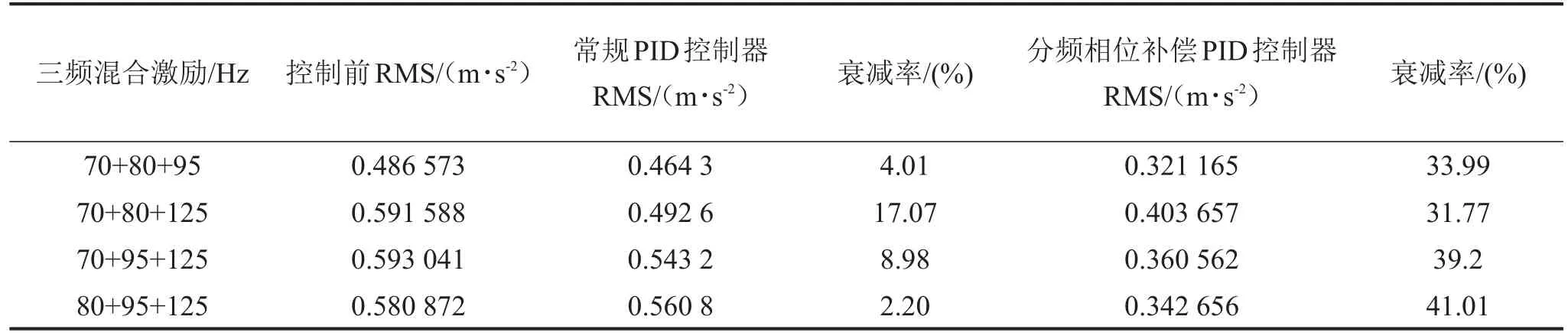
表7 三频激励下分频滞后补偿前后加速度均方值及衰减率对比

图10 70 Hz+80 Hz+95 Hz三频激励控制效果

参考文献：

[1]WU D F,HUANG L,PAN B,et al.Experimental study and numerical simulation of active vibration control of a highly flexible beam using piezoelectric intelligent material[J].Aerospace Science&Technology.2014,37:

[2]SAM PAUL P,VARADARAJAN A S.Effect of impact mass on tool vibration and cutting performance during turning of hardened AISI4340 steel[J].Romanian Journal ofAcoustics and Vibration,2014,11:154-163.

[3]杨智春，王巍，谷迎松，等.一种弯曲型压电堆作动器的设计及在振动控制中的应用[J].振动与冲击，2009，28(9)：30-134.

[4]LIAO W H,WANG D H.Semiactive vibration control of train suspension systems via magnetorheological dampers[J].Journalof IntelligentMaterialSystems &Structures,2003,14(3):161-172.

[5]PHAPALE V B,MANUEL G,ELENA B,et al.Modal active vibration control of a rotor using piezoelectric stack actuators[J].Journal of Vibration&Control.2007,13(1):45-64.

[6]DU H,SZE K,LAM J.Semi-active H-infinity control of vehicle suspension with magneto-rheological dampers[J].Journal of Sound and Vibration,2005,283(3-5):981-996.

[7]MARY P M,MARIMUTHU N S.Design of self-tuning fuzzy logic controller for the control of an unknown industrial process[J].Iet Control Theory &Applications,2009,3(4):428-436.

[8]FU J,YU M,XING Z W.PID controlfor magnetorheological elastomer absorber with impact load[J].Applied Mechanics&Materials,2011,121-126:1734-1738.

[9]ÅSTRÖM,JOHAN K,HÄGGLUND T.Advanced PID Control[M].ISA-The Instrumentation,Systems,And Automation Publishing,2006.

[10]KAYA I.Obtaining controller parameters for a new PI-PD Smith predictor using autotuning[J].Journal of Process Control,2003,13(5):465-472.

[11]LIU T,CAI Y Z,GU D Y,et al.New modified Smith predictor scheme for integrating and unstable processes with time delay[J].IEE Proceedings-Control Theory andApplications,2005,152(2):238-246.

[12]CHEN J,WANG L,DU B.Modified internal model control for chemical unstable processes with time-delay[C].2008 7 th World Congress on Intelligent Control and Automation,2008:6353-6358.

[13]李敏，王琪，靳其兵.不稳定时滞对象的改进内模直接控制[J]. 计算机工程与设计，2016，37(2)：493-498.

[14]YANG F,GUPTA A,KUO S M.Parallel multi-frequency narrowband active noise control systems[C].Acous tics，Speech and SignalProcessing,IEEE International Conference,IEEE,2009:253-256.