现代有轨电车诱发的大地振动特性分析

罗 锟，汪振国，雷晓燕，孙 滨

（华东交通大学 铁路环境振动与噪声教育部工程研究中心，南昌 330013）

近年来，现代有轨电车以其节能环保、安全快捷等优点，在我国呈现出蓬勃发展之态。截至2016年5月，我国现代有轨电车规划线路累计超过6 000 km，2020年前需建设的线路长度已超过2 600 km，现代有轨电车线路的规划速度越来越快，并开始从一线城市向二、三线城市发展[1]。

在此背景下，对现代有轨电车开展研究已成必然。专家学者们在有轨电车的动力学性能、线路、轮轨接触、适用性等方面做了大量的科学研究[2-5]，推动了有轨电车行业在我国的发展。然而，城市轨道交通的发展必然会伴随着振动与噪声问题的出现，振动是七大环境公害之一，又是噪声之源，城市轨道交通所产生的环境振动对人体身心健康、建筑结构的安全以及精密仪器的正常使用都具有很大的影响[6-7]。目前，针对铁道车辆所致环境振动问题，学者们主要将研究集中在地铁、货车、动车等方面[7-9]，而现代有轨电车作为城市轨道交通的一部分，其诱发的环境振动问题却鲜有文献报道。

本文为研究现代有轨电车诱发的大地振动传播规律及衰减特性，总结以往学者们利用Simpack软件实现轮轨耦合的方法，分析其中的优缺点，进而提出一种轮轨耦合仿真的新方法，并利用该方法建立现代有轨电车-无砟轨道-大地的3维耦合振动分析模型，对有轨电车诱发的大地振动特性进行分析，以期为我国有轨电车的发展及其诱发的大地振动减振控制提供参考。

1 轮轨耦合方法概述

在多体动力学软件Simpack中，有两种实现轮轨耦合的方法：引入哑元法和利用Simpack软件中柔性轨道模块实现轮轨耦合[10]。虽然两种方法均具有各自独特的优点，但在轮轨作用力耦合方面还存在一定的缺陷。

引入哑元法的核心思想是把钢轨或轨道结构用质量及其微小的物体（哑元）代替，如图1所示。

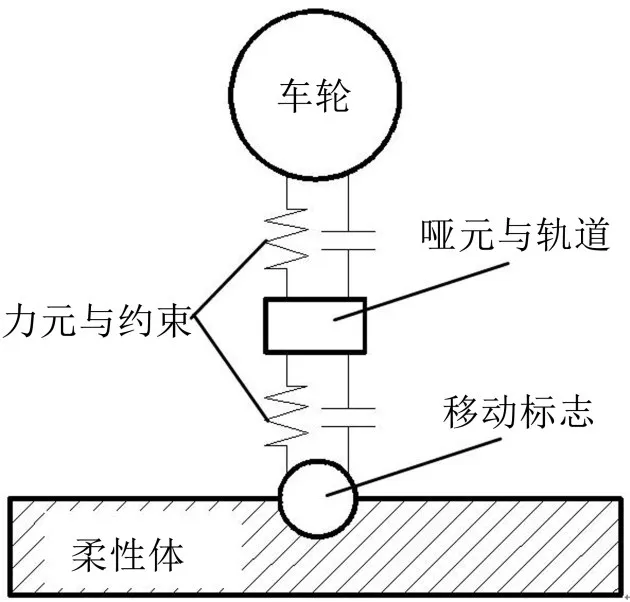
图1 引入哑元法原理图示

在数学中哑元表示不干扰同一表达式中其他变量的局部变量，因而不会影响与之连接的部件，通过哑元的传递作用便可实现车辆与轨下结构间作用力的交换。

多体系统中将变形相对较大的物体视作柔性体，轨下结构属于柔性体。Simpack软件的柔性轨道模块可快速实现车辆与柔性体的作用力耦合，该方法的核心思想是直接将耦合系统视为整体，把轨下结构的柔性体信息读入程序求解器，与车辆模型共同求解。此时，车辆与轨下结构之间只通过接触离散点实现作用力的交换，即该方法是用接触离散点代替钢轨和轨道结构。

可以发现，以上两种方法在实现轮轨耦合的过程中，都采用了简化替代的做法，这种做法的好处是在保证结果精度的前提下能极大提高计算效率，然而，这也给耦合模型造成了一定的局限性。比如钢轨和轨道结构的振动响应就无法考虑。本文利用Simpack软件的柔性轨道模块，并结合自编的钢轨*.ftr文件，提出一种能解决耦合模型局限性的建模方法，在下文中将对该方法进行详细阐述。

2 耦合振动分析模型

车轨耦合振动分析模型以轮轨接触面为界，将耦合系统分成两个子系统，即上部车辆多刚体系统和下部钢轨、轨道板以及其他轨下结构组成的多柔体系统。两个子系统通过轮轨接触模型实现耦合。

2.1 车辆多刚体系统

铁道车辆属典型的多自由度（DOF）、小位移多体系统，车体与转向架、转向架与轮对以及转向架内部各组成部分之间只发生相对微小的运动。Simpack中车辆模型是由主模型与子模型构成的，它们之间通过改变虚体的铰接位置实现车辆整体模型的建立。图2为本文现代有轨电车的主模型与子模型的拓扑图。

图2 单节车辆拓扑图

整个车辆系统包括多个物体，动力学模型中可将这些弹性相对很小的物体看做刚体，忽略其弹性变形，将车辆模型视为多刚体系统。

2.2 多柔体系统

耦合模型中的钢轨、轨道结构以及轨下各结构，这些结构在耦合振动分析中都要考虑它们的变形与振动响应，因而在多体系统中需将这些结构考虑为柔性体。利用Ansys建立各结构的有限元实体模型，再应用有限元动力子结构技术分别对各结构的有限元模型进行处理，输出3个必要的信息文件：*.sub、*.tcms以及*.cdb。其中，*.sub文件包含结构的质量矩阵和刚度矩阵信息；*.tcms文件包含结构的模态信息；*.cdb文件为结构的几何外形信息文件。之后通过Simpack的接口程序，将上述3个信息文件转换成Simpack识别的柔性体文件*.fbi，Simpack软件读取该文件信息，便在多体系统中生成各结构的柔性体模型。再通过力元连接各柔性体，即可构成多柔体系统，如图3所示。

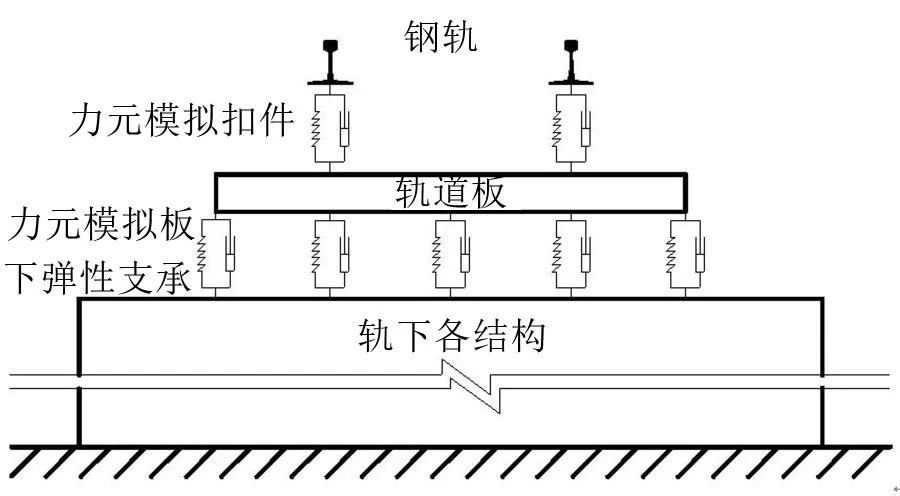
图3 多柔体系统

2.3 轮轨耦合实现方式

2.3.1 钢轨的*.ftr文件

钢轨顶面为轮轨接触面，车轮与钢轨在轮轨接触面上相互作用，因此，若能在钢轨上定义节点，便可通过力元连接钢轨节点和下部结构柔性体上的标志，从而实现车辆多刚体系统与轨下结构多柔体系统的耦合。

利用Simpack柔性轨道模块，结合自编的*.ftr文件即可实现钢轨上节点的定义。*.ftr文件是通过软件识别柔性体位置、节点信息的配置文件，针对柔性钢轨，可用该文件来说明柔性钢轨位置、轮轨接触离散点分布、节点刚度阻尼、节点误差等信息。*.ftr文件的命令形式和编制规则可参考Simpack软件的帮助文档。

将编辑好的钢轨*.ftr文件与钢轨*.fbi柔性体文件一起放在模型数据目录下，Simpack柔性轨道模块读取钢轨数据时便能识别节点信息。由此可见，实现轮轨耦合只需对钢轨进行处理，而对轨下结构没有任何特殊的要求，因而本文的轮轨耦合方法不仅适用于车辆与大地间的耦合，也适用于车辆与桥梁或者其他轨道结构间的耦合。

2.3.2 轮轨接触模型

轮轨接触模型有刚性接触和弹性接触两种方式，如图4所示。采用刚性接触模型能极大提高求解速度，但车辆实际运行过程中，轮轨之间可能出现跳轨现象，刚性接触模型不能模拟此类现象。采用弹性接触模型相当于在轮轨间增加了1个弹簧-阻尼力元，当轮轨间接触时，轮轨间法向力大小等于弹簧-阻尼力，当轮轨间不接触时，轮轨间法向力为0[11]。

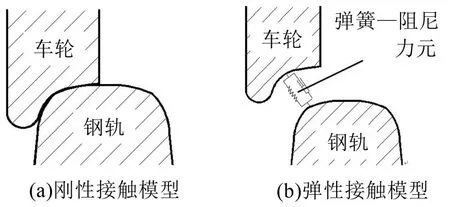
图4 轮轨接触模型

文中轮轨接触模型结合了两种模型的特点：当轮轨接触时，采用刚性接触模型计算轮轨力，当轮轨间不接触时，轮轨力为0。

2.4 轮轨耦合方法验证

采用文献[12]中的车辆及浮置板式轨道结构参数，利用文中轮轨耦合方法建立车辆-浮置板式轨道耦合振动分析模型，如图5所示。

图5 车辆-浮置板式轨道耦合振动分析模型

计算单节地铁车辆以60 km/h的速度运行时系统的竖向振动响应，并与文献[12]和文献[13]的计算结果对比，列于表1。

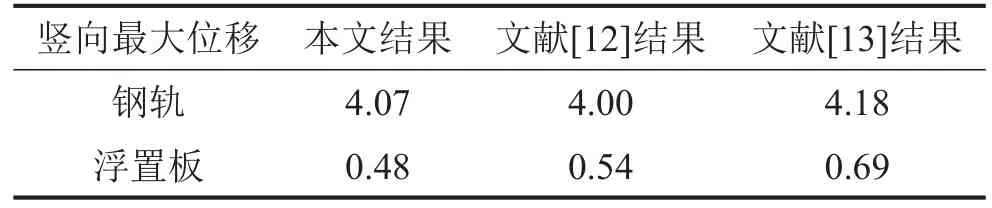
表1 本文计算结果与文献[12-13]计算结果对比/mm

由表1可知，本文计算结果与文献[12-13]计算结果基本吻合，初步验证了本文耦合方法的正确性。

3 车辆-大地耦合模型及计算参数

3.1 现代有轨电车模型

每节车辆中部正下方设有转向架，每个转向架由两个轮对和构架组成，整车模型的建立是通过改变主模型与转向架子模型间虚体的铰接位置实现的，如图2所示。轮对模型参照传统轮对建立，其与钢轨的接触模型结合刚性接触和弹性接触两种方式，故计算模型中各物体均具有6个方向自由度（6DOF），单节车辆共计24个自由度，如表2所示。

表2 单节车辆自由度

本文有轨电车全车由4个模块组成，其中两节车为1组，整列车共两组，车体与车体间通过铰接装置实现四节车辆编组挂接，如图6所示。

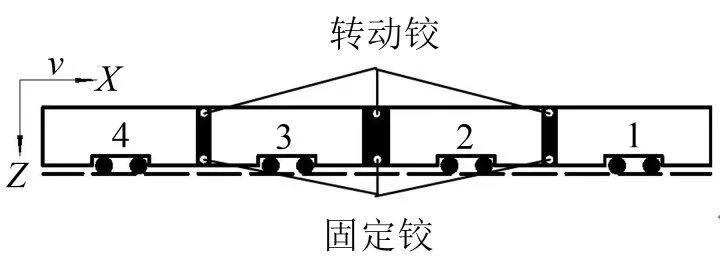
图6 有轨电车编组与铰接图示

图6中1、2车为1组，3、4车为1组。参考有轨电车铰接装置的实际设置情况，在单节车辆模型之间通过6个铰接实现整车模型的建立，每节车辆之间上、下铰接各1个，且全部设置在铰接区域的中间位置，上部铰接为转动铰，下部铰接为固定铰。建模时，采用X、Y、Z3个位移方向的大刚度弹簧阻尼力元模拟固定铰，以限制车体下部在这3个方向的相对位移；采用X、Y方向的大刚度弹簧阻尼力元模拟1、2车与3、4车之间的转动铰，以传递上部车体间的纵向力，并限制其在X、Y向的相对位移；2、3车间的转动铰采用X方向的大刚度弹簧力元模拟，以传递纵向力，且保证两组车能在上部区域3个方向上有相对运动。模型中车辆建模基本参数部分取自文献[14]，部分由部件生产商提供。

3.2 多柔体系统

本文耦合模型中多柔体系统由钢轨、轨道板、路基与大地组成，其中钢轨采用CHN60轨，其与轨道板通过弹簧阻尼力元连接，用以模拟扣件，轨道板截面尺寸为2 400 mm×190 mm（宽×高），长60 m。轨道板与路基间同样采用弹簧阻尼力元连接，用以模拟板下弹性支承。

我国目前尚无有轨电车路基结构的设计规范，且各城市设计修建有轨电车的路基结构均具有差异。文献[15]结合我国现行铁路路基基床结构与国内在建或已建有轨电车基床结构，通过对轨道荷载-路基动应力、变形与强度分析，指出我国有轨电车路基在设置0.2 m厚的混凝土支撑层时，基床厚度应取1.2 m，其中，基床表层厚度为0.4 m，基床底层厚度为0.8 m。支撑层位于轨道板以下，为混凝土填筑。本文以文献[15]建议的无砟轨道有轨电车基床结构形式为参照，建立路基基床模型。在建立路基模型时，把车辆动荷载与路基面上的静载按45º扩散角向大地扩散，因而在模型中将路基基床结构设计为底边内角为45º的等腰梯形。

大地土层模型参照成都某有轨电车试验段大地土层结构建立[16]，长和宽均设计为60 m。为避免大地模型在计算时发生因边界处理不当而造成的计算失真现象，将大地模型的边界设计为黏弹性人工边界，黏弹性人工边界具有良好的高频和低频稳定性，本文在大地的有限元模型中便引入此种边界，具体做法是：在大地3维有限元模型的边界上沿边界面法向延伸1层与土体单元厚度相等的实体单元，并将其外层节点全约束[17]。图7为多柔体系统组成图示。

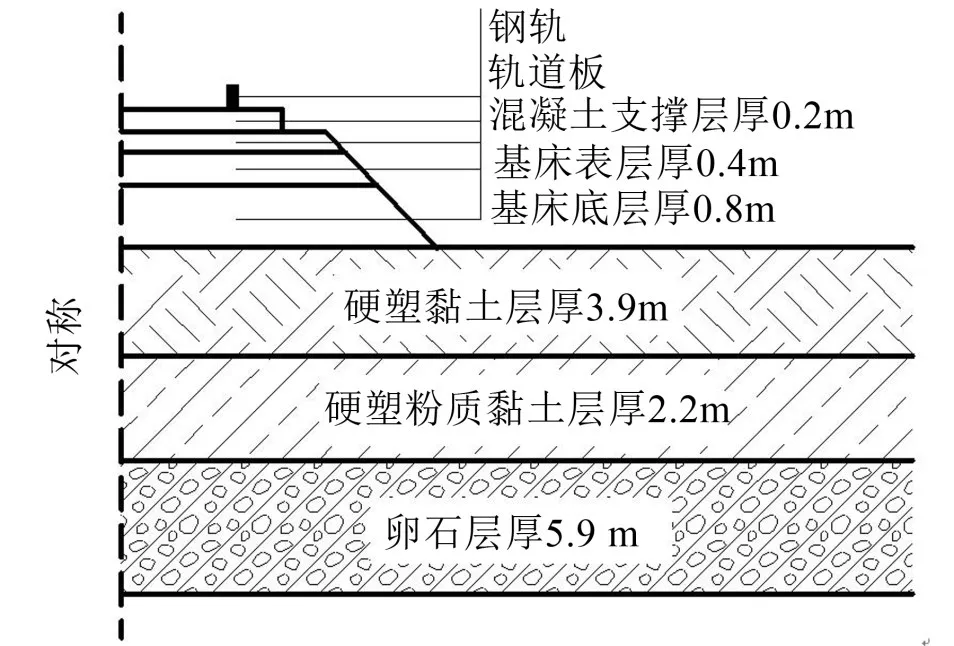
图7 多柔体系统组成

表3给出各结构的计算参数。表4为连接件的计算参数。

表3 多柔体系统各结构计算参数

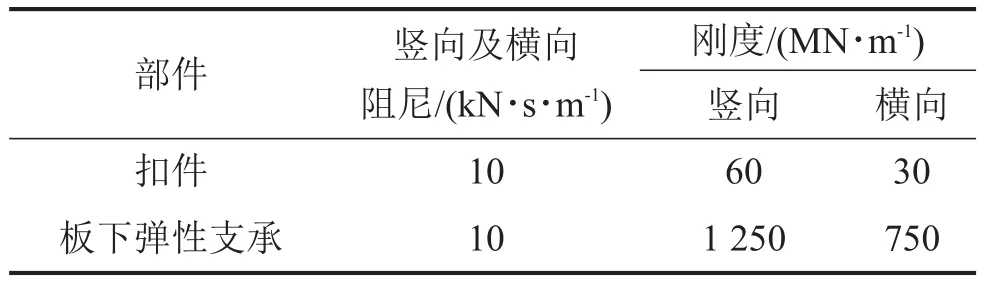
表4 连接部件计算参数

利用上文介绍的轮轨耦合方法，将现代有轨电车多刚体系统与多柔体系统进行耦合，建立现代有轨电车-无砟轨道-大地的3维精细化耦合振动模型，如图8所示。

图8 现代有轨电车-无砟轨道-大地耦合振动模型

线路施加美国5级竖向及横向不平顺作为轨道激励，车辆运行速度为70 km/h，计算时间4.5 s，步长200 Hz。

4 结果分析

4.1 观测点布置

本文选择纵向中心截面为特征截面，在该截面上沿大地横向及竖向选择观测点，研究振动在两个方向上的传播规律，如图9所示，在特征截面上，沿大地表面横向布置8个测点（H1－H8），沿轨道中心线正下方竖向每个结构层上布置1个测点，共6个竖向测点（S1－S6）。

4.2 大地振动响应分析

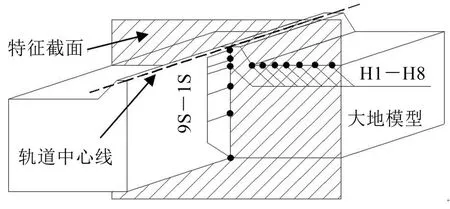
图9 特征截面与观测点布置

对耦合系统进行求解，得到各观测点的位移及加速度振动响应最大值如图10所示。从图10可以看出：各观测点的竖向振动均大于横向振动，故在研究有轨电车诱发的大地振动问题时，应重点关注竖向振动情况；振动的衰减速度与距振源距离的远近有关，距振源越近，振动衰减越快。

图11为大地表面及特征截面深度方向的振动响应云图，从图11可以看出：大地表面振动在距轨道中心线大约10 m的距离内迅速衰减，超过10 m后衰减变缓；沿深度传播的振动大约在深度为6 m的范围内迅速衰减，超过6 m衰减速度变缓。

4.3 大地表面振动衰减规律分析

为研究大地表面振动在传播过程中的能量衰减规律，选择距轨道中心线10 m左右范围内的观测点H1、H2、H3和H4，对各测点的竖向加速度时程数据进行功率谱密度（PSD）分析，图12为各测点的PSD曲线。

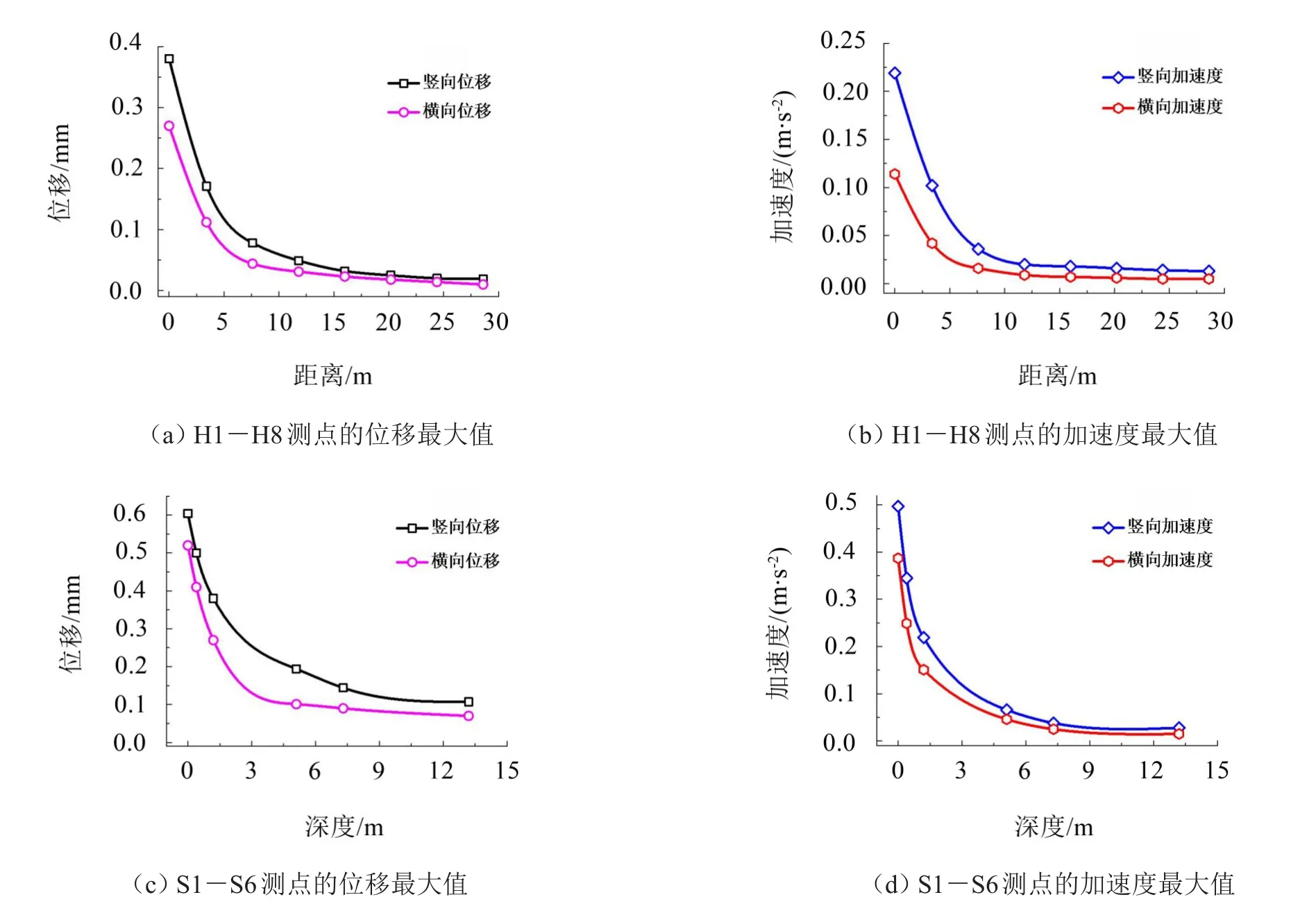
图10 各观测点振动响应最大值

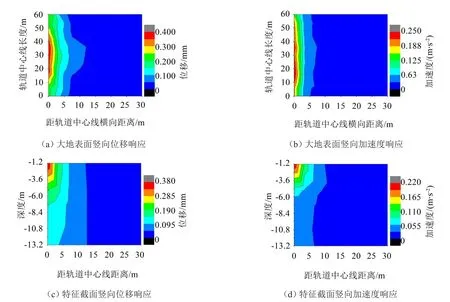
图11 大地表面及特征截面竖向振动响应云图

由图12可知：距离振源最近的H1测点峰值频率较多，主频为30.6 Hz，这是由轨道不平顺激励引起的；随着距离的增加，其他观测点峰值频率减少，主频均为6.3 Hz，且各测点主频峰值相近，这与大地振动的频散特性相关，振动在大地传播时，低频振动衰减慢，高频振动衰减快。

为能更好反应振动在某一频率上的衰减量，将各测点的竖向加速度时程转换为1/3倍频程的振动加速度级频谱，如图13所示。图14为H 1测点至H 4测点的振动衰减量。

由图13可知：各观测点在4 Hz与6.3 Hz时的振动衰减很慢，H1测点至H4测点的振动加速度级衰减量分别为7.5 dB与6 dB，其余频率对应的衰减量均在10 dB以上，如图14所示；H2测点在6.3 Hz的振动加速度级比H1测点在该频率的振动加速度级大，出现“振动放大”现象，这是因为大地主频为6.3 Hz，当激振频率与大地主频相近时便出现“振动放大”现象。

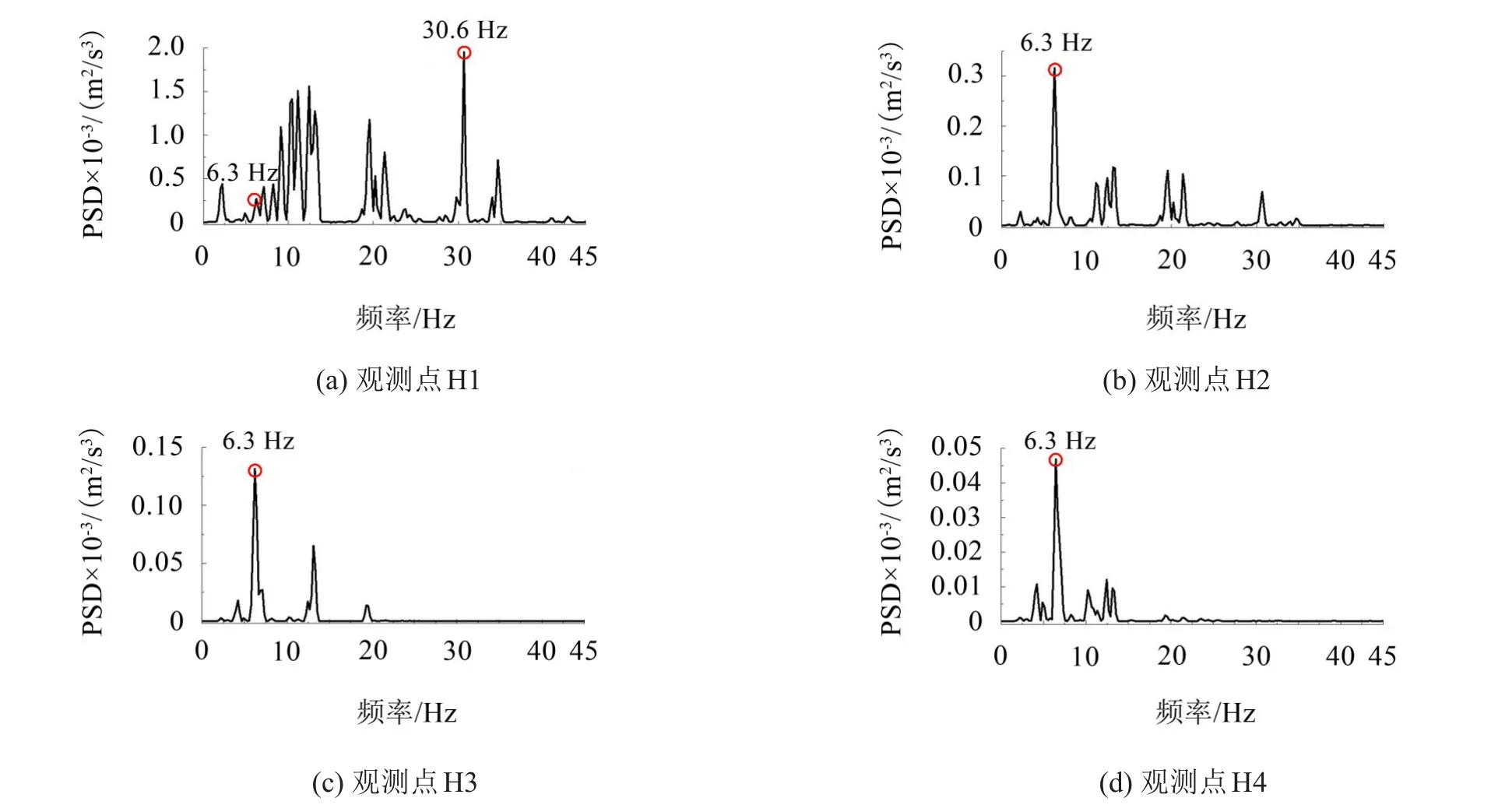
图12 各观测点的PSD曲线

图13 振动加速度级的1/3倍频程频谱图

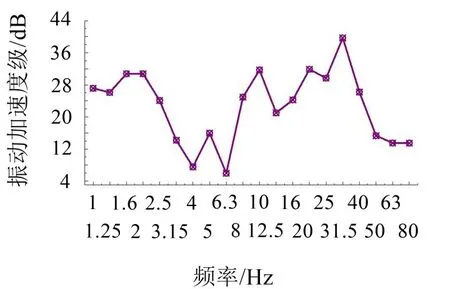
图14 H1测点至H4测点振动衰减量

5 结语

（1）本文采用的轮轨耦合方法可以克服以往Simpack实现轮轨耦合的局限性，应用该方法建立的耦合振动模型能全面分析耦合系统各结构的振动，且该方法不仅适用于车辆与大地间的耦合，也适用于车辆与桥梁或者其他轨道结构间的耦合。

（2）在研究有轨电车诱发的大地振动问题时，应重点关注竖向振动情况；大地表面振动在距轨道中心线大约10 m的距离内迅速衰减，超过10 m后衰减变缓；沿深度传播的振动大约在深度为6 m的范围内迅速衰减，超过6 m衰减速度变缓。

（3）距离振源越近，峰值频率越多，距振源最近的观测点主频为30.6 Hz，这是由轨道不平顺激励引起的；随着距离的增加，较大的峰值频率减少，主频变为6.3 Hz，且各测点主频峰值相近，这与大地振动的频散特性相关，振动在大地传播时，低频振动衰减慢，高频振动衰减快。

（4）大地表面在4 Hz与6.3 Hz时的振动衰减很慢，且在6.3 Hz时会出现“振动放大”现象，这是因为大地振动的主频为6.3 Hz，当激振频率与大地振动主频相近时便出现“振动放大”现象。

参考文献：

[1]周淮.我国现代有轨电车发展现状与需要研究的若干问题[J]. 交通与港航，2017，4(1)：15-20.

[2]李创，孙守光，任尊松，等.独立车轮转向架车辆曲线通过性能分析[J].北方交通大学学报，2003，27(5)：86-89．

[3]赵伟，王春艳，张军，等.有轨电车轮轨型面匹配问题的研究[J]. 铁道学报，2011，33(2)：34-37.

[4]吕凤梅，赵建秋，闰晓明，等.100%低地板现代城市有轨电车限界和小曲线通过能力分析[J].铁道车辆，2013，51(9)：5-7.

[5]王艳彩，黄新.现代有轨电车的地区适用条件[J].交通标准化，2011，(2)：127-129.

[6]曹宇静.城市轨道交通环境影响评价振动预测模型对比分析[J]. 噪声与振动控制，2017，37(2)：192-196.

[7]魏军,雷晓燕.地铁列车引起的大地振动传播规律研究[J].轨道交通，2009(11)：67-71.

[8]张鹏飞，雷晓燕，高亮，等.铁路环境振动对厂房内精密仪器的影响分析[J].振动与冲击，2013，32(16)：187-192.

[9]刘庆杰，雷晓燕，许士强，等.高架轨道系统诱发环境振动的实测与数值分析[J].铁道工程学报，2008，25(5)：23-29.

[10]周昱.基于Simpack和Ansys的铁路车桥耦合振动仿真分析[D].成都：西南交通大学，2013.

[11]崔圣爱，祝兵，黄志堂.基于多体系统动力学和有限元法的联合仿真在车桥耦合振动研究中的应用[J].计算机应用研究，2009，26(12)：4581-4584.

[12]王丹.广州地铁二号线浮置板轨道振动特性分析[D].成都：西南交通大学，2005.

[13]向俊，王阳，赫丹，等.城市轨道交通列车-浮置板式轨道系统竖向振动模型[J].中南大学学报(自然科学版)，2008，39(3)：596-601.

[14]吴师.现代有轨电车轨道结构力学分析方法及设计关键技术研究[D].北京：北京交通大学，2014.

[15]顾成权.无砟轨道有轨电车路基基床结构探讨[J].路基工程，2015(1)：68-71.

[16]何雨.有轨电车路基荷载特征与结构设计[D].成都：西南交通大学，2016.

[17]谷音，刘晶波，杜义欣.三维一致黏弹性人工边界及等效黏弹性边界单元[J]. 工程力学，2007，24(12)：31-37.