库车前陆盆地“三超”气井产能预测方法对比

马 群 王胜军 蒋国军 何 飞 郭宇恒 胡家荣

（1.中国石油塔里木油田公司库车油气开发部，新疆 库尔勒 841000；2.中国石油塔里木油田公司开发事业部 新疆 库尔勒 841000）

0 引言

无阻流量是描述气井产能的重要指标之一，是确定气井合理工作制度的重要依据，一般通过产能试井得到，继产能试井之后，又相继提出了单点试井、等时试井等方法，上述测试方法所获得的产能多数是以二项式分析方法以及指数式分析方法为基础完成的［1］。但对于库车前陆盆地地质构造极为复杂、地层压力超高（122 MPa大于100 MPa）、埋藏超深（7 000 m大于6 000 m）、地层温度超高（168℃）的典型“三超”气井［2］来说，进行产能测试不仅面临较大困难，而且压力超高，超出压力平方二项式产能方程适用范围［3］，进而导致传统方法不能获得理想的预测效果。基于此，寻找一种预测准确且方便的“三超”气井产能预测方法尤为重要。笔者以keS区块为研究工区，利用收集到的气井静态资料结合探井资料，建立多元线性回归、BP神经网络、支持向量机3种预测模型，运用建立好的预测模型对检验样本进行产能预测，根据其预测结果优选一种适合库车前陆盆地“三超”气井产能预测的新方法。

1 气井产能预测方法研究

在气田开发过程中影响气井无阻流量的因素有很多，据前人对气井产能预测的研究［4-5］可知，影响气井产能的因素主要有储层渗透率、测井孔隙度、含水饱和度、气层有效厚度、地层压力、地层系数、裂缝密度、地层温度、天然气相对密度和临界压力。收集到的KeS区块共31口井所组成的数据集见表1。

1.1 基于多元线性回归的单井产能预测

多元线性回归的单井产能预测其原理是用多个影响因素作为自变量线性表示因变量的变化。假定因变量和自变量参数之间存在如下线性关系：

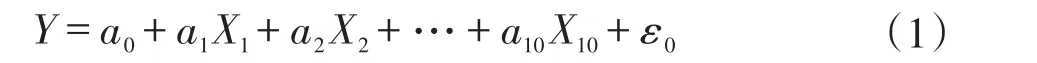
式中，Y为可观测的随机变量；ai为自变量系数（i＝0，1，2，3，…，10），也称回归系数；X1为储层渗透率，mD；X2为孔隙度，%；X3为气层有效厚度，m；X4为地层压力，MPa；X5为含水饱和度，%；X6为地层系数，mD·m；X7为裂缝密度，条／m；X8为地层温度，℃；X9为天然气相对密度；X10为临界压力，MPa；ε0为不可观测的随机误差。

利用本次收集到的31口单井数据构建相应模型。利用建立的模型在SPSS软件中对31口井的数据进行了综合分析，得出主要影响因素的影响程度，即相关系数R和判定系数R2（判定线性回归的拟合程度）。由该模型拟合的相关系数R为0.895可知，相关性较好；R2为0.801（大于0.8），则拟合结果较为理想。运用SPSS软件对基于多元线性回归的单井产能预测模型进行求解，得到相关系数，将相关系数带入公式（1）得回归拟合公式（2），进而可预测气井产能，其预测结果见图1。

表1 样本数据集表

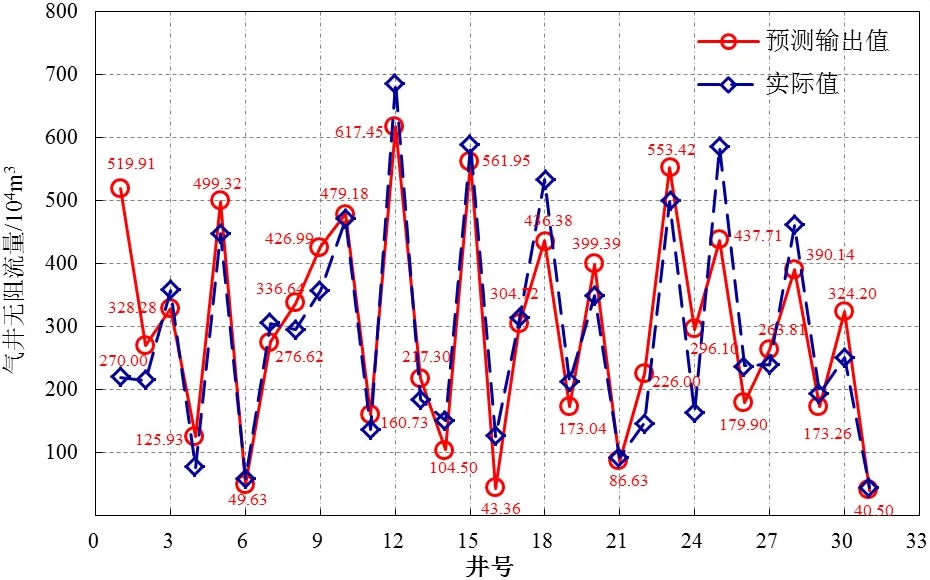
图1 多元线性回归预测结果图

1.2 基于BP神经网络的单井产能预测

BP神经网络是1956年由Rumelhart和Meeelland为首的科学家小组提出［6］，它实际上是一个非线性多元回归方法，包括输入层、隐含层和输出层，上下层之间实现全连接，而每层神经元之间无连接［7］。输入样本从输入层经隐含层逐层传递至输出层，如果输出层的实际输出与期望输出的误差在允许程度内，则结束学习算法；如果输出层的实际输出与期望输出的误差较大，则转至误差反向传播，即输出误差通过隐含层反向直至输入层，在反传过程中将误差分摊给各层的各个单元，获得各层各单元的误差信号，作为其修正各单元权值的依据［8］，这一计算过程使用梯度下降法完成。在不停地调整各层神经元的权值和阈值过程中就是模型学习训练的过程。

基于BP神经网络的非线性函数拟合算法流程可以分为BP神经网络构建、BP神经网络训练以及BP神经网络预测3个步骤，按照上述步骤开展气井产能预测研究。BP神经网络构建根据非线性函数的特点确定BP神经网络结构，由于气井产能预测的非线性函数有10个输入参数，1个输出参数，所以BP神经网络结构为10-8-1，即输入层有10个节点，隐含层有8个节点（可以进行调整，值越大表明训练越精确，但消耗时间越长），输出层有1个节点。网络参数配置：迭代次数80次，学习率0.01以及学习目标为4.0×10-4，用表1中的前26组数据作为训练样本对网络模型进行训练学习，用训练好的模型对表1中的后5组数据进行预测计算，其预测结果见图2。

1.3 基于支持向量机的单井产能预测

支持向量机是Corinna Cortes和Vapnik等人于1995年在统计学习理论中结构风险最小化理论基础之上提出的［9］，与BP神经网络相比，克服了过学习和局部极值等问题，在解决小样本、非线性及高维模式识别中表现出许多特有的优势。支持向量机主要解决分类和回归两类问题，而气井产能预测属于其回归范畴［4］34，利用支持向量机函数逼近的回归算法，其回归函数f可表示为［10］：

图2 BP神经网络预测结果图

式中，x∈Rn为输入变量；w∈Rn为权值矢量；b∈R为偏差。

采用结构风险最小化原则，将式（1）转化为求解下列函数的最优解：

对于上述凸规划问题，可转化为以下对偶形式［11］：

引入核函数，通过非线性映射函数Φ将数据样本映射到一个高维特征空间，再在高维特征空间中完成内积运算。最终，非线性问题的SVM回归方程可表示为：

根据其原理建立产能预测模型［12］，在模型建立过程中，最主要的工作是选择合适的参数对（惩罚参数C与核函数基宽g），它们的合理确定直接影响所建模型的预测精度和推广能力。本次研究运用最为普遍的交叉验证网格搜索方法［13］来确定优化参数，而C、g值越小，其模型的预测精度越高，推广能力越强。在精细网格搜索选择计算下可以得到最佳参数对（C，g）＝（11.313 7，0.062 5）。

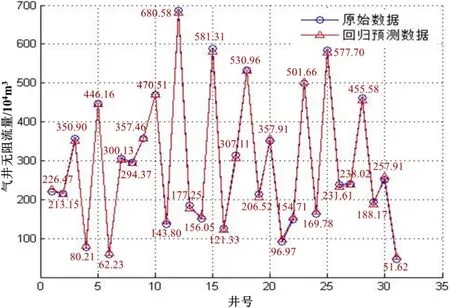
图3 支持向量机模型回归预测结果图

2 预测结果对比分析

1）由上述3种方法的预测结果（表2）可知，多元线性回归、BP神经网络的预测结果不稳定，相对误差较大，平均相对误差分别为14.99%、17.60%，而支持向量机预测精度高，预测结果稳定，平均相对误差仅为4.34%。

2）支持向量机是由BP神经网络发展而来，具有适应性强、理论完备、训练时间短、泛华能力强等优点，在处理小样本学习问题上具有的独到优越性［14］，克服了BP神经网络局部极小值以及对统计样本依赖大的问题；其次支持向量机预测方法操作简便，易实现，而BP神经网络结构选择困难，一般只能依靠经验选定，因此在用BP神经网络预测时需要具备丰富的操作经验和知识储备。

3）气井产能预测属于非线性研究的范畴，用多元线性回归方法预测，预测精度较差，预测结果不稳定，而本次研究是利用支持向量机预测的非线性回归问题，因此预测精度远高于多元线性回归方法。

综上所述，支持向量机方法为库车前陆盆地“三超”气井产能快速准确预测提供了一个新的途径，同时，也为同类气井产能预测提供了可借鉴的方法。

表2 单井产能预测相对误差统计表

3 结论

1）根据气井静态资料结合探井资料，建立了多元线性回归、BP神经网络和支持向量机3种气井产能的预测模型，利用表1中的后5组数据对3种模型进行了检验，由预测结果可知，3种方法预测结果的平均相对误差分别为14.99%、17.60%、4.34%。

2）由气井产能预测结果可知，支持向量机方法比多元线性回归方法和BP神经网络方法的预测结果稳定，预测精度高；通过3种产能预测方法优缺点对比分析可知，支持向量机克服了BP神经网络与多元线性回归的缺点，具有适应性强、泛华能力强、训练时间短和操作简便易实现等优点；综上所述，支持向量机方法为库车前陆盆地“三超”气井产能快速准确预测提供了一个新的途径。

3）研究中所建立的基于支持向量机的产能预测模型仅适用于本区块的气井产能预测。若在其他区块应用时需结合实际情况，合理选择数据样本，重新建立预测模型才能得到有效的结果。

［1］唐洪俊，徐春碧，唐皓.气井产能预测方法的研究与进展［J］. 特种油气藏，2011，18（5）：11-15.

［2］赵益秋.试油完井一体化技术在“三超”气井中的应用［J］. 钻采工艺，2017，40（3）：53-56.

［3］李勇，刘启国，郜国喜，等.塔里木油田气井无阻流量计算公式探讨［J］. 新疆石油地质，2004，25（1）：72-73

［4］李月丽，伊向艺，卢渊，等.基于支持向量机的气井新井产能预测［J］. 油气田地面工程，2010，29（1）：34-36.

［5］许玲，陈德民，赖枫鹏.气井新井产能预测的神经网络方法研究［J］. 油气井测试，2008，17（3）：12-14.

［6］ Dayhoff J E，Deleo J M.Artifieial neural networks［J］.Caneer，200l，91（8）：1 615-1 634.

［7］尹琅，任山，颜晋川，等.神经网络预测法在沙溪庙气藏压前评估中的应用［J］.天然气技术与经济，2012，6（6）：27-29.

［8］沈花玉，王兆霞，高成耀，等.BP神经网络隐含层单元数的确定［J］. 天津理工大学学报，2008，24（5）：13-15.

［9］克里斯蒂亚尼尼.支持向量机导论［M］.李国正，王猛，曾华军，译.北京：电子工业出版社，2004.

［10］虞朝阳，马群，郑鹏宇.基于改进支持向量机的压裂效果预测方法研究［J］.重庆科技学院学报：自然科学版，2016，18（3）：116-118.

［11］ Keerthi S，Shevade S，Bhattcharyya C.A fast iterative nearest point algorithm for support vector machine clas⁃sifierdesign［J］.IEEE Transactions on NeuralNet⁃work，2000，11（1）：124-136.

［12］董雁萍.支持向量机预测模型的构建及其应用［D］.西安：西安理工大学，2010.

［13］童凯军，单钰铭，李海鹏，等.支持向量回归机在气井产能预测中的应用［J］.新疆石油地质，2008，29（3）：382-384.

［14］张亚军，刘志刚，霍柏超，等.基于支持向量机的电力负荷组合预测模型［J］.电力需求侧管理，2007，9（2）：14-17.