一种部分森林覆盖环境电波传播特性预测方法
刘晓娣,朱四华,林洪文
(海军航空大学,山东烟台264001)
森林是电波传播常见的复杂环境,会引起电波的反射、折射、绕射等现象,影响着无线通信系统、雷达系统的性能。目前,关于森林环境的电波传播已有大量实验和理论研究[1-8]。Tamir[3]指出对2~200 MHz的电磁波森林可等效为大气与地面间的均匀有耗介质,并结合大量实验提出了著名的Tamir侧面波模型。李乐伟[5]、Sarabandi[6-7]等采用解析法求解了森林环境的电波传播问题,但在电波远距离传播时,计算量大,耗时多,实用性不强。抛物方程(Parabolic Equation,PE)是一种全波法,能同时处理非均匀媒介和复杂边界条件,采用傅里叶算法可实现快速求解[9-11]。若将森林视为均匀有耗介质层,其等效介电常数非常接近于1,则可用PE预测森林环境的电波传播特性[12-16]。森林植被情况不同,对电波传播的影响不同,其等效介电常数也不同。采用PE求解森林覆盖环境的电波传播问题时,为减小计算误差,对于较大的等效介电常数,应减小水平步长[13]。
在实际应用中,很多无线通信系统的收发终端位于森林的外部。Holm[14-15]、郭建炎[16]等采用PE求解了部分森林覆盖山区的电波传播问题,效果较好,但在整个计算域内步进求解时都采用均匀的水平步长。在部分森林覆盖环境的整个计算域内,若根据森林的等效介电常数选取步长,则会消耗更多的计算时间;若根据光秃地面区域的等效介电常数选取步长,又会增大森林覆盖区域的计算误差。
针对部分森林覆盖环境电波传播特性预测问题,本文提出基于动态网格的PE法。采用宽角PE研究部分森林覆盖环境的电波传播特性,并通过分步傅里叶变换(Split-Step Fourier Transform,SSFT)实现快速求解;为保证计算精度,减少计算时间,引入动态网格技术,根据电波传播路径上森林覆盖情况、不同森林区域的等效介电常数,动态设置PE的水平步长;通过数值仿真验证了该方法的有效性。
1 PE法
假设电波在无源媒介中传播,电磁场的时谐因子为e-iωt。在直角坐标系中,假设标量ψ是与y方向无关的任一电磁场分量,可得到二维标量波动方程:

式(1)中:k=2π/λ为真空中的传播常数,λ为电波波长;x、z分别表示直角坐标系下的传播距离和传播高度;m=n+z/ae为修正折射指数,是传播媒介的折射指数,ae为地球的半径。
假设电磁波的主要能量沿x轴正向传播,定义波函数:

将式(2)代入式(1)可得:
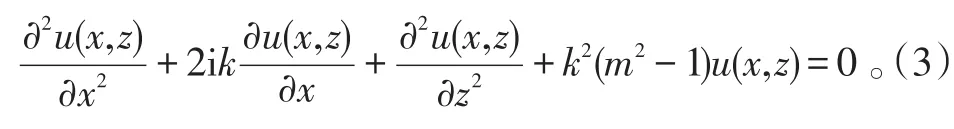
对式(3)进行因式分解并只考虑电波的前向传播,采用Feit-Fleck近似法[17],得到Feit-Fleck型宽角抛物方程:

利用SSFT求解可得:

式(5)中:u(x,z)为当前步进的场分布;Δx为水平步长;p=ksinα表示z的频域变化量;α为每一步进上的入射余角;F、F-1分别表示傅里叶变换与逆变换。
2 部分森林覆盖环境中的动态网格技术
若将森林等效为均匀有耗介质,其等效介电常数为εc,等效折射指数是一个复数,虚部反映电波传播产生的电导损耗。在部分森林覆盖环境中,森林覆盖区域,电波传播的地面以上半空间可视为由森林吸收层和森林以上标准大气层构成;光秃地面区域,地面以上半空间为大气单一媒介。由于森林的密度、植被种类、季节变化等差异,在不同森林覆盖区域的等效介电常数不同,等效折射指数也不同。因此,部分森林覆盖环境中折射指数n在x方向是分段变化的,但在每一大段上n与x无关。由文献[18]可知,在部分森林覆盖的整个传播路径下可用PE法求解。
由式(5)可知,采用SSFT求解PE时,通常情况下在整个计算区域内,水平步长Δx是一个固定值。但在部分森林覆盖环境中,折射指数n在x方向分段变化,各分段区域的等效介电常数存在差异。文献[13]研究发现,森林覆盖环境中,在相同等效介电常数下,PE的计算误差随步长增大呈增大趋势;在相同步长情况下,等效介电常数越大,PE的计算误差越大。因此,在一定误差范围内,PE应随着等效介电常数的增大而减小水平步长。
在部分森林覆盖环境中,为减小n在x方向上分段变化带来的误差,提高电波传播预测的准确性,引入动态网格技术,根据不同森林区域的等效介电常数动态确定水平网格步长。
假设在水平计算域x范围内,根据传播路径上的森林分布情况、不同森林区域的等效介电常数,将水平网格步长分为J类,其中最小步长为Δxmin,最大步长为Δxmax,第 j类对应的步长为Δxj,则

其中,Δxj需根据所在区域的等效介电常数与计算精度而定[13,18]。
根据上述约束条件,动态网格在部分森林覆盖环境中的应用见图1。图1中,在光秃地面区域,采用粗网格划分,取 Δxj-1=Δxmax;在Forest 1、Forest 2区域,分别根据其等效介电常数确定该区域的水平网格步长,由于Forest 1的介电常数相对于Forest 2要小,因而Δxj>Δxj+1。
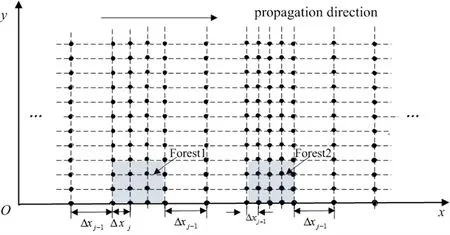
图1 部分森林覆盖环境的动态网格示意图Fig.1 Dynamic grid map in partly forest environments
3 数值仿真
为验证本方法的有效性,采用基于动态网格的PE法分析了部分森林覆盖环境的电波传播特性,并与PE采用均匀细网格、均匀粗网格的计算结果进行比较。
假设在标准大气条件下,电波在平坦地表边界上传播。发射天线高度10 m、频率100 MHz、高斯天线方向图,方向图的3dB宽度为3°,水平极化。地表的相对介电常数为20,电导率为10 ms/m。距离发射天线2~5km处有一稀疏的树林,高15 m,等效介电常数为1.01+i0.02;8~12km处有一浓密的树林覆盖,高18 m,等效介电常数为1.06+i0.10;最大传播距离为15km。分别采用PE的均匀细网格、均匀粗网格和动态网格预测电波在该区域的传播损耗,其中均匀细网格的步长为10 m,均匀粗网格的步长为100 m,动态网格的最大步长100 m、最小步长10 m,并根据森林等效介电常数调整步长,具体的步长设置如图2所示。

图2 动态网格的步长设置示意图Fig.2 Step distribution map of the dynamic grid
图3显示了电波在部分森林覆盖环境中的传播损耗。图3 a)为采用动态网格的计算结果,图3 b)为采用均匀粗网格的计算结果。从图3 a)中可以看出,森林覆盖区域的传播损耗大于光秃地面,且浓密树林的传播损耗高于稀疏树林;森林区域的颜色从左上方至右下方逐渐变深,传播损耗逐渐增大,这表明森林是一种可穿透的媒介,且树林越浓密,可穿透性越差,这与文献[1]的分析一致;而在离开树林后的附近区域,传播损耗依然较大,随着距离的增大,传播损耗逐渐减小,这是因为在离开树林后的近距离处,经森林的透射电磁场起主要作用,在远距离处绕射电磁场起主要作用,透射波的传播损耗远大于绕射波的损耗。由图3 b)可以看出,采用均匀粗网格的计算结果在森林与大气交界处,传播损耗由大到小的渐变过程不明显,电磁场变化跨度较大,尤其是浓密树林,这说明粗网格对森林的可穿透性表征较差,不能有效反映电波在森林区域的传播情况。
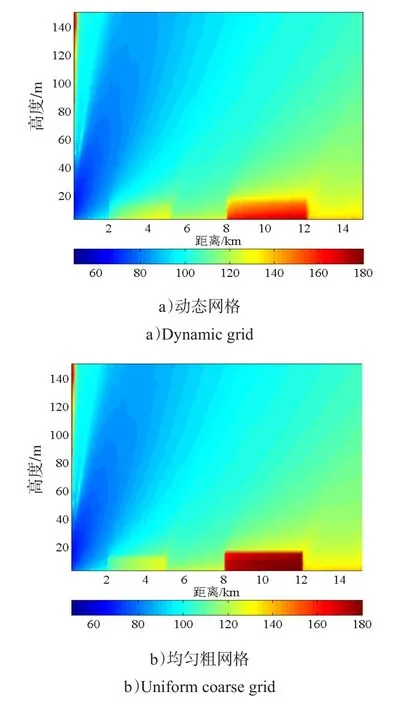
图3 电波在部分森林覆盖环境中的传播损耗Fig.3 Propagation loss in partly forest environments
图4给出了不同接收高度上电波传播损耗随距离的变化情况。在图4 a)中,接收高度为9 m,低于森林高度,森林覆盖区域的传播损耗明显高于光秃地面,且树林越浓密,损耗越大,最大相差约35dB;相比于均匀细网格,均匀粗网格的计算结果偏大,且树林越浓密误差越大,对于同一片树林在电波离开的边缘误差最大,接近25dB;而动态网格的计算结果与均匀细网格的十分吻合,由此证明了动态网格的正确性。在图4 b)中,接收高度为50 m,高于森林高度,森林对电波传播的影响变小,森林覆盖区域的传播损耗与光秃地面相差最大不足5dB,这时3种网格的计算结果基本一致。图5给出了电波在最大距离15km处的传播损耗随高度的变化情况,从图中也可以看出,在该距离处,部分森林覆盖的传播损耗与光秃地面相差不大,森林对电磁场影响很小,此时3种网格的计算结果也基本一致。

图4 电波在不同接收高度处的传播损耗Fig.4 Propagation loss in different heights

图5 电波在最大传播距离处的传播损耗Fig.5 Propagation loss at the maximum distance
表1为PE分别采用均匀细网格和动态网格计算时的水平网格数和计算时间的对比关系。由表1可知,在相同仿真环境下,本算例采用动态网格后,PE计算所需的水平网格数相对于均匀细网格下降了57.3%,所需的计算时间减少了69.1%,这表明采用动态网格能极大地减少PE计算所需的内存和时间,更具高效性。由此可见,在部分森林覆盖环境的电波传播问题中引入动态网格技术能够极大提高仿真效率。

表1 水平网格数和计算时间对比Tab.1 Comparison of horizontal grid number and computational time
4 结论
针对部分森林覆盖环境的电波传播问题,提出基于动态网格的PE法。采用宽角PE预测电波传播特性,并引入动态网格技术平衡PE求解的准确性与时效性问题。通过仿真算例,分析了电波在部分森林覆盖环境中的传播特性,探讨了引入动态网格技术的有效性。结果表明:在计算精度相似的情况下,相对于均匀细网格,动态网格会大大减少PE计算所需的网格空间与计算时间,而相比均匀粗网格具有更高的计算精度。可见,采用基于动态网格的PE法预测部分森林覆盖环境的电波传播问题更具高效性。
[1]M LE PAUL.Propagation modeling of VHF radio channel in forest environments[C]//IEEE Military Communications Conference.IEEE,2004:609-614.
[2]张青洪,廖成,盛楠,等.森林环境电波传播抛物方程模型的改进研究[J].物理学报,2013,62(20):204101.ZHANG QINGHONG,LIAO CHENG,SHENG NAN,et al.Improved study on parabolic equation model for radio wave propagation in forest[J].Acta Physical Sinia,2013,62(20):204101.(in Chinese)
[3]TAMIR T.On radio-wave propagation in forest environments[J].IEEE Transactions on Antennas and Propagation,1967,15(6):806-817.
[4]KOVACS I Z,EGGERS PF,OLESEN K.Radio channel characterization for forest environments in the VHF and UHF frequency bands[C]//IEEE 50thVehicular Technology Conference.Amsterdam:IEEE,1999:1387-1391.
[5]LI L W,KOH J H,YEO T S,et al.Analysis of electromagnetic wave propagation in forest environment along multiple paths[J].Journal of Electromagnetic Wave and Applications,1999,13(8):1057-1059.
[6]SARABANDI K,KOH I S.Effect of canopy-air interface roughness on HF-VHF wave propagation in forest[J].IEEE Transactions on Antennas and Propagation,2002,50(2):111-121.
[7]WANG F N,SARABANDI K.A physics-based statistical model for wave propagation through foliage[J].IEEE Transactions on Antennas and Propagation,2007,55(3):958-968.
[8]刘立国,王海松,史晓新,等.树冠中电波传播路径损耗的研究及模型的建立[J].电波科学学报,2006,21(6):910-914.LIU LIGUO,WANG HAISONG,SHI XIAOXIN,et al.Modeling of propagation path loss in a canopy[J].Chinese Journal of Radio Science,2006,21(6):910-914.(in Chinese)
[9]KUTTLER J R,DOCKERY G D.Theoretical description of the parabolic approximation/Fourier split-step method of representing electromagnetic propagation in the troposphere[J].Radio Science,1991,26(2):381-393.
[10]来嘉哲,方广有,刘帅.战场电磁环境构建中的抛物方程应用研究[J].雷达学报,2012,1(3):63-68.LAI JIAZHE,FANG GUANGYOU,LIU SHUAI.Research on constructing war-field electromagnetic environment using parabolic equation[J].Journal of Radars,2012,1(3):63-68.(in Chinese)
[11]刘晓娣,周新力,侯松高.电波传播抛物方程模型在航空通信中的应用[J].电讯技术,2016,56(6):624-628.LIU XIAODI,ZHOU XINLI,HOU SONGGAO.Application of wave propagation model based on parabolic equation in aeronautical communication[J].Telecommunication Engineering,2016,56(6):624-628.(in Chinese)
[12]SOUZA J F,MAGNO F N B,VALENTE Z A,et al.Mobile radio propagation along mixed paths in forest environment using parabolic equation[J].Mircrowave and Optical Technology Letters,2009,51(4):1133-1136
[13]ARSHAD K,KATSRIKU F,LASEBAE A.Radio wave VHF propagation modeling in forest using finite elements[J].IEEE ICTTA,2006,2:2146-2149.
[14]HOLM P,ERIKSSON G,KRANS P,et al.Wave propagation over a forest edge—parabolic equation modeling vs.measurements[C]//IEEE Symposium on Personal,Indoor,and Mobile Radio Communication,Lisbon,Portugal.IEEE,2002:140-145.
[15]HOLM P,WAERN A.Wave propagation over a forest edge-parabolic equation modeling vs measurements[C]//2003 IEEE Symposium on EMC.Istanbul:IEEE,2003:764-767.
[16]郭建炎,王剑莹,龙云亮,等.基于抛物方程法的部分森林覆盖山区电波传播分析[J].电波科学学报,2008,23(6):1045-1056.GUO JIANYAN,WANG JIANYING,LONG YUNLIANG,et al.Analysis of radio propagation in partly forested terrain environment using parabolic equation approach[J].Chinese Journal of Radio Science,2008,23(6):1045-1050.(in Chinese)
[17]FEIT M D,FLECK J A.Light propagation in graded-index fibers[J].Applied Optics,1978,17(24):3990-3998.
[18]胡绘斌,毛钧杰,柴舜连.电波传播中求解宽角抛物方程的误差分析[J].电波科学学报,2006,21(2):199-203.HU HUIBIN,MAO JUNJIE,CHAI SHUNLIAN.Error analysis of wide-angle parabolic equation for radio propagation[J].Chinese Journal of Radio Science,2006,21(2):199-203.

