浅谈相关分析与回归分析的关系

郝依寒

（河北省石家庄市正定实验中学，石家庄 050800）

随着时代的进步，数学与人类的联系也逐渐加深，如今人类活动更是离不开数学的帮助，统计学是应用数学中与我们实际生活联系较为紧密的一类分支，是帮助我们解决问题的工具。其中相关分析、回归分析等在我们的生活中运用也是十分广泛的，本文通过研究相关分析与回归分析的概念与分类，列举回归分析的具体应用，分析相关分析与回归分析的异同。

1 相关分析

相关分析和生活往往是紧密相连的，小到买卖时钱财上的加加减减，大到应用数学模型解决棘手复杂的问题。例如，我们走出家门踏上地铁时，我们所乘车的路程与你需支付的乘车费用便是一种相关关系即正相关。相关分析是研究随机变量之间的依存关系，从而研究他们的相关程度即研究变量间的相关关系。

1.1 函数关系与相关关系

函数关系是我们经常接触的一种关系。当一个或几个变量取一定的值时，另一个变量有惟一确定的值与之相对应，那么我们就称这种关系为函数关系。函数关系是一种确定性关系，自变量与因变量之间是一一对应的，一个自变量只有一个惟一自变量的值与之对应。例如，对于同一根弹簧来说（即弹性限度k相同），弹力（F）大小与其伸长量（Δx）的关系（F=kΔx）。

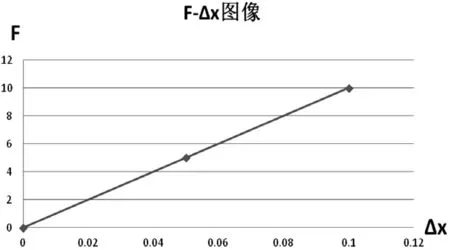
图1 弹簧弹力与其伸长量关系图

相关关系也指变量之间的相互关系，但在相关关系中，一个变量的值往往受多个变量的影响，即当变量X取某个固定值时，变量还会受到其他因素的影响，导致变量取值不确定。所以这种相关关系不同于函数关系，它不能用函数关系精确表达。例如，一个人的工作效率与其是否熬夜的关系。一个人如果熬夜，那么他的工总效率不一定很低，因为工作效率还会受到其他一些因素的影响。

1.2 相关关系分类

相关关系有多种分类方法。按程度分，可分为完全相关、不完全相关和不相关。其中完全相关本质上就是函数关系；不相关是指变量之间无影响，又称零相关；不完全相关是指变量之间存在不严格依存关系。在现实生活中，不完全相关关系出现较多，因为实际生活中偶然因素对研究对象的影响较大，所以几乎不可能出现完全相关关系。在相关分析中，不完全相关也是我们主要的研究对象。按方向可分为正相关和负相关。正相关是指一个变量随另一个变量的增加（减少）而增加（减少），即两者变化同方向，如数学上我们很熟悉的圆的周长L=2πr，L随r的增大而增大；而负相关则反之。按相关的形式可分为线性相关和非线性相关。按变量多少可分为单相关，偏相关和复相关。

1.3 相关系数

相关系数是研究变量间线性相关程度的量。它最早由统计学家卡尔·皮尔逊提出，一般用r表示。卡尔·皮尔逊在阅读高尔顿的《自然遗传》是对“相关”这一概念十分着迷，于是深入研究，才有了我们今天看到的相关系数。相关系数是大于等于-1小于等于1的。相关系数为-1时表示变量间完全负相关；大于-1小于0表示变量之间为负相关关系；等于0时表示变量之间不相关；大于零小于1时，表示变量之间呈正相关关系；等于1时，表示变量之间成完全正相关。相关系数的绝对值接近1表示变量之间相关程度越高。

除了相关系数，相关表和相关图可以更加直观形象地反映两变量间的相关关系及相关方向，但无法确切描述表现出两变量间的相关程度，只能从图中看出大致的趋势，因此在相关分析中，相关系数能够帮助我们更加精确的分析和研究变量之间的关系。

2 回归分析及其应用

在统计学中，回归分析指的是确定两种及以上变量间相互依赖的定量关系的一种统计方法，而“回归”一词是由英国著名生物学家兼统计学家高尔顿（Francis Galton，1822～1911.）在研究人类身高遗传问题时提出来的。高尔顿搜集了1078对父亲及其儿子的身高数据并通过研究发现这些数据的散点图大致呈直线状态，即从整体上来看，父代身高与子代身高呈正相关关系。然后高尔顿对试验数据进行了深入的分析研究，发现子代平均身高普遍具有接近父代平均身高的趋势，于是高尔顿把这种现象成为回归效应。

现在我们所说的回归分析是确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法。研究两个变量间的关系，需要我们确定预测的具体目标即因变量，另一变量则为自变量，再通过调查得到数据，接着对数据进行分析从而确定两变量间的关系；探究人寿命的长短与酗酒程度的关系时，我们可以把人的寿命长度看作因变量y，把酗酒程度当作自变量x，通过走访调查获得足够的数据资料，经过严密的计算与分析得出结论。

2.1 回归分析分类

回归分析可以有多种分类方式：按照涉及变量多少，分为一元回归分析和多元回归分析；按照因变量多少，分为简单回归分析和多重回归分析；按照自变量与因变量之间的关系类型，分为线性回归和非线性回归。但是在实际研究当中，非线性回归往往比较复杂。在研究初速度为0的物体的匀加速直线运动的实验中，通过将实验数据画出x-t图像，得到的是一条曲线从图像中无法精确判断出其回归方程。所以我们可以采用化曲为直的思想，用时间的平方代替时间，我们得到的就是一条直线。这样就可以更直观的展现出位移与时间的关系。但是很多时候无法将变量替换，或需将变量间原本的关系表现出来，所以并不是所有的回归分析都需要表示非线性回归，化曲为直的思想在统计学中是有局限性的，非线性回归在统计学中也是有很重要的作用和意义的。

图2 匀加速直线运动x-t²图像

图3 匀加速直线运动x-t图像

2.2 回归分析的应用

人类回归分析的研究已有很长时间，但是回归分析在当代仍然有其自己的意义与作用。回归分析一般通过分析现象间的具体形式确定其因果关系并用数学模型表现出来。在经济方面，回归分析可以帮助我们了解经济市场的动向，帮助我们作出判断，例如：现代的商人在采购销售上往往会采用回归分析的方式对以往的数据进行分析处理，结合目前市场形式得出经营的方法，从而减少自身损失的风险；如果研究商品品质与其销量间的关系，从实践上看，商品品质会影响商品销量，则我们可以以商品品质为自变量，商品销售量为因变量，运用统计学方法分析变量，当商品质量提升时，商品的销售量也会随之提升。建立数学模型得出商品品质与销量间的回归直线方程。在科学研究方面，回归分析可以帮助我们更加准确的得到两个或者多个事物之间的联系，为科学研究者提供思路与方向，在教育方面，我们可以借助回归分析改进教育方法等等。

3 相关分析与回归分析的异同

3.1 相同点

对于相关分析与回归分析，这二者之间是有一定联系的。它们都是用来研究变量之间关系的统计学方法。可以说，相关分析是回归分析的基础，回归分析是相关分析的深入和继续。现实中，在分析数据时我们往往先通过相关分析来确定变量间的相关程度，再通过回归分析深入研究建立数学模型。若使用回归分析前没有对变量进行相关分析，则很难保证变量间有很强的相关关系，则此时进行回归分析时得出的结论往往不准确，易造成错误，此时我们成这种错误为虚假回归。如，欲研究手机待机时间与使用者年龄之间的关系时，倘若先不对其进行相关分析而直接进行回归分析，则就会将这两种毫无关系的变量强行联系在一起，产生了虚假回归，得到错误结论，对消费者进行误导。故应把这两种分析方法结合使用，以达到准确研究和分析的目的。

3.2 不同点

相关分析中，变量间关系对等，即不存在确定的因果关系，不存在一个变量因为另一个变量的变化而变化，也没有自变量与因变量之分。而回归分析变量间的关系不对等，变量与变量之间存在一定因果关系。相关关系只是用以确定变量之间是否存在一定的联系，并简单的研究这两个变量间的相关关系，并不能确定具体的变量变化趋势，所以我们说相关分析中无固定的自变量与因变量。而回归分析中，自变量是确定的，而因变量是随自变量的变化而变化的，且自变量与因变量的关系往往不能互换，一个自变量往往受到多个因变量的影响，且通过数据分析得到的回归方程往往与实际不相等，存在一定的波动。相关分析的相关系数是惟一确定的，即对于相关分析来说只有一个衡量标准，相关系数只有一个且惟一确定，而且我们在分析数据时只考虑相关系数；而回归分析中的变量关系并不惟一确定，回归分析中往往会具有两个或两个以上的衡量标准。回归分析变量之间具有因果性，因变量会随自变量的变化而变化，且因变量往往受多个自变量的影响，故可能出现多个回归方程。

4 结束语

综上所述，相关分析只是用来研究变量间相关关系的方法，不能定量分析数据而回归分析为我们定量分析数据提供了一种方法比。在相关分析的基础上对数据进行回归分析，比仅仅通过相关分析得出的结论更加准确。所以这种建立回归模型的方法也被应用到我们日常生活的许多地方中。不仅如此，随着时代的发展，人们对回归分析的研究还有望加深，从而改进现在的建立应用回归模型的技术手段，所以，深入探究回归分析也不乏具有一定现实意义。

[1] 张尧庭.多元统计分析引论[J].北京：科学出版社，2003（9）.

[2] 张林泉.相关分析与回归分析应用辩解[J].哈尔滨职业技术学院学报，2010（4）：123-124.

[3] 孙莹，孙明涛.相关和回归分析的关系及其预测价值研究[J].南北桥，2009（5）.

[4] 王娟.对统计中相关分析与回归分析的论述[J].经管视线，2014（8）：115.