浅析基于带通数字滤波器的信号解调及其仿真

张孝磊

（聊城大学，聊城 252000）

1 理想带通滤波器的特性分析

设第l个子载频的带通滤波器的传递函数为Hl（ω），Hl（ω）的表达式为：

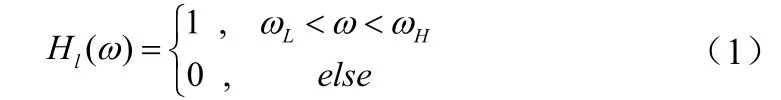
式中，带通滤波器中心频率为（ωL+ωH）/2=fl，带宽为ωH-ωL=Δf。对应的时域响应为 hl（t），则其输出为第 l个子载频的回波信号：

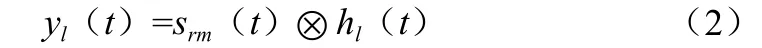
卷积的计算比较复杂，由于时域的卷积等效于频域的乘积，在实际的应用中，通常利用信号的频域形式与滤波器的幅频响应相乘获得滤波结果：

式中，Yl（f）、Srm（f）、Hl（f）分别是 yl（t）、srm（t）、hl（t）的频域形式。

值得说明的是：如果OFDM后续处理需要利用相位信息，则滤波器的相位特性必须要做到严格的线性相位，如FIR滤波器；如果后续处理不需要利用相位信息，则选择幅频响应特性较好的滤波器即可。例如巴特沃斯滤波器。

巴特沃斯滤波器的幅频响应和相频响应曲线如下。

运行结果如图1（a）（b）（c）所示。巴特沃斯滤波器的幅频响应比较理想，具有非线性相位。由滤波器的损耗函数曲线可以看出，在fs=12kHz时，衰减为30dB，即通带指标有富余。

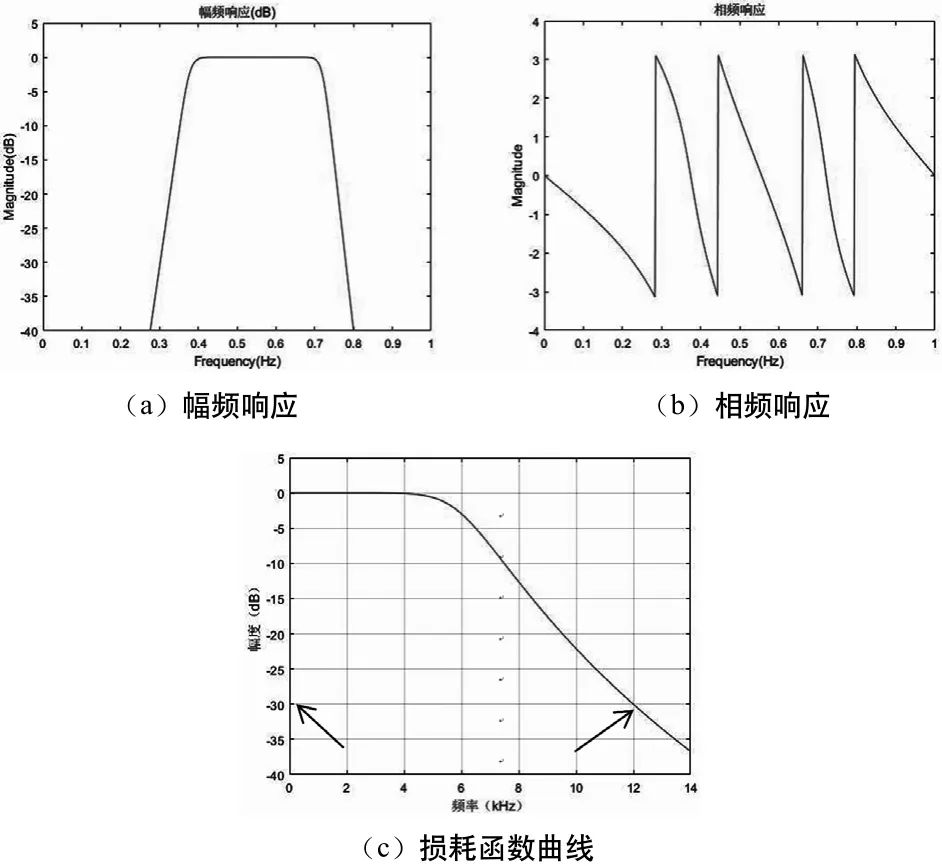
图1 巴特沃思滤波器的幅频响应、相频响应及损耗函数曲线

巴特沃斯滤波器的频率特性曲线，无论是在通带还是阻带都是频率的单调减函数。因此，当通带边界处满足指标要求时，通带内会有大量富余量。

2 OFDM信号的解调

设OFDM信号中心频率f0=1GHz，脉冲宽度Tp=0.1μs，子载频频率间隔Δf=10MHz，子载频个数N=16，合成带宽B=160MHz，wn=1。设采样频率fs=640MHz，信号的时域波形和频谱如图2所示。OFDM时域信号是一个sinc函数的形式，由于频率加权系数wn=1，因此其频谱是一个矩形窗的形状。

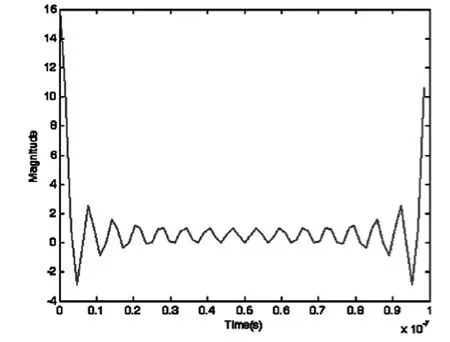
图2 （a）时域信号

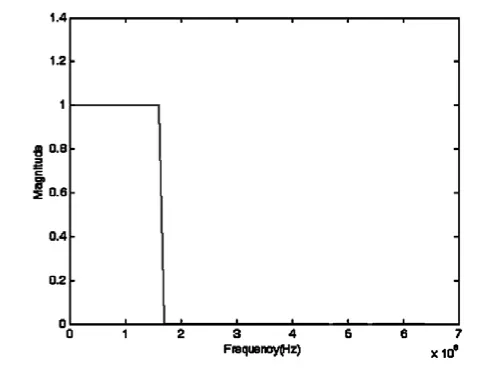
图2 （b）频谱

运行得到的FIR滤波器的幅频响应如图3所示，选用的窗函数为汉宁窗。将OFDM信号通过FIR滤波器，得到滤波后的结果如图4所示，可以看出，滤波可以获得OFDM信号的某一个子载频信号。

图3 FIR带通滤波器幅频响应

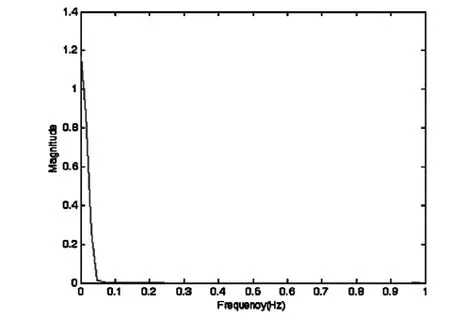
图4 OFDM信号滤波后输出信号

若采用限制最小方差法设计FIR滤波器，将OFDM雷达信号通过FIR滤波器，可以看出，采用限制最小方差法设计FIR滤波器与窗函数设计的滤波器获得解调的结果相差不大。

3 结束语

限于篇幅，无法把程序代码展示出来。作为一名通信类本科生，灵活运用了所学知识，结合Matlab软件进行仿真设计，综合分析了巴特沃斯滤波器的幅频响应特性和OFDM信号的输出信号。通过阅读专业课本以及网上资料查阅，进一步加深了对数字带通滤波器和OFDM信号特性的理解，为以后进一步研究打下了基础。

[1] 丛玉良，王宏志 数字信号处理原理及其MATLAB实现[M].北京：电子工业出版社，2006.