适应于弱电网的永磁直驱风电机组虚拟惯量协调控制策略
贺家发, 宋美艳, 兰 洲, 黄林彬, 辛焕海, 汪 震
(1. 浙江大学电气工程学院, 浙江省杭州市 310027; 2. 西安交通大学电气工程学院, 陕西省西安市 710049; 3. 国网浙江省电力公司经济技术研究院, 浙江省杭州市 310006)
0 引言
随着风力发电的迅速发展,大规模接入电网的风电机组给电力系统稳定运行带来了不容忽视的影响[1-2]。例如:在风电机组替代同步发电机的过程中,电力系统中由同步发电机提供的转动惯量将逐渐减小,进而削弱了电力系统的频率调节能力[3-4]。为此,现代电网逐渐要求风电机组参与到电网的频率调节中,并在电网频率波动时为电网提供有功功率支撑[5]。
目前,已有很多文献对风机的频率调节策略进行了研究[6-8]。这些频率调节策略主要通过建立电网频率与风机有功功率输出之间的关系来实现风机的频率调节[9]。其中,有功—频率下垂控制是将频率偏差信号(Δf)引入风机有功或转矩控制中,而虚拟惯量控制是将频率微分信号(df/dt)引入风机有功或转矩控制中[10]。应用这些频率调节策略时,风电机组仍采用锁相环(PLL)实现与电网的同步,但在弱电网即短路比(SCR)较小的电网下,锁相环动态性能变差,严重时甚至会导致风机系统的失稳[11]。虚拟同步控制是解决这一由锁相环引起的稳定问题的重要手段[12-15]。
虚拟同步控制通过模拟同步发电机的特性从而实现并网自同步及虚拟惯量模拟,因此在变流器的控制中不再需要锁相环作为同步单元。并且,这类虚拟同步控制可以推广应用于双馈风力发电机中,使其在提供频率支撑的同时,也能够适应于弱电网的运行条件[16-17]。
然而,上述虚拟同步控制主要应用在功率控制型变流器中[18],这类变流器的有功及无功功率由控制策略决定,其运行的前提是直流电压恒定。而永磁直驱风电机组的并网变流器一般为直流电压控制型变流器,这类变流器通过控制器中的直流电压控制环将直流电容电压控制在设定值,其输出的有功功率则由直流电容另一端的流入功率决定[19]。因此,这种控制策略不能直接应用在直驱风电机组的并网变流器中。文献[15]提出了一种可应用于直流电压控制型变流器的虚拟同步控制,该控制方法利用直流电容动态实现并网自同步,将这种虚拟同步控制应用到直驱风电机组中可以保障其在弱电网下的稳定性。但是,这种虚拟同步控制利用直流电容的储能为电网提供功率支撑,考虑到直驱风电机组中直流电容储能远小于其桨叶存储的旋转动能,应利用其旋转动能提供功率支撑,并尽量减小其直流电压的波动。
为此,本文提出一种针对永磁直驱风电机组的虚拟惯量协调控制策略。该策略在机侧变流器控制中引入了虚拟惯量控制,利用风机的旋转动能提供惯量支撑所需的能量;在网侧变流器控制中引入了虚拟同步控制,利用直流电容动态实现其并网自同步。该策略使直驱风电机组不仅能利用其存储的旋转动能为电网提供虚拟惯量,而且使风机能适应于弱电网运行。基于MATLAB/Simulink的电磁暂态仿真验证了所提出控制策略的有效性。
1 虚拟惯量协调控制策略
永磁直驱风电机组常经LCL滤波器接入交流电网,如图1所示,其中机侧变流器控制输出有功功率并实现最大功率点跟踪(MPPT),而网侧变流器控制直流电压的稳定。图1同时给出了本文所提出的虚拟惯量协调控制策略的控制结构。其中,PWT为电机的有功功率输出;Pg为网侧变流器输出到电网的有功功率;CDC为直流电容;CF为LCL滤波器的滤波电容;LF为变流器侧的滤波电感;Lg为电网侧的滤波电感;Ll为变压器的漏感与线路电感之和,为了简化分析,忽略了线路电阻。下面对虚拟惯量协调控制策略的控制实现进行具体说明。

图1 永磁直驱风电机组并网系统电路和控制框图Fig.1 Circuit and control block diagram of grid-connected system of PMSG-based wind turbine
1.1 机侧变流器控制
在机侧变流器控制中,采用虚拟惯量控制实现风机的惯量模拟,其主要原理是将电网频率微分信号(df/dt)引入有功功率参考值中,从而建立风机有功功率输出与电网频率的联系。如图1所示,虚拟惯量控制的方程为:
(1)

1.2 网侧变流器控制
在网侧变流器控制中,采用虚拟同步控制实现变流器的并网自同步,其包含直流电压控制器、无功—电压下垂控制器、内环控制器及电流前馈控制器。其中,内环控制器采用了交流电压控制和交流电流控制的级联结构,由于当前已有很多文献对这种级联结构进行研究[21-22],此处不再赘述。
1.2.1直流电压控制器
在虚拟同步控制中,直流电压控制器不仅能够控制直流电压稳定,而且能利用直流电容动态实现网侧变流器的并网自同步[15],如图1所示。其控制方程为:
(2)

值得一提的是,附加的锁相环只是为了获取电网频率的稳态值,不用于实现并网同步。
该虚拟同步控制的并网自同步机理将在第2节进一步讨论。
1.2.2无功—电压下垂控制
无功—电压下垂控制使直驱风电机组具有电压支撑能力,如图1所示,其基本的控制方程为:
Vref-V0=KQ(Q0-QE)
(3)
式中:Vref为无功—电压下垂控制的输出电压幅值参考值;V0为电压幅值给定值;KQ为无功—电压下垂系数;Q0和QE分别为无功功率给定值和输出值。
1.2.3电流前馈控制器
由于直驱风电机组在电网频率波动时需要提供功率支撑,这将导致在暂态过程中直流电容两侧功率不平衡,从而引起直流电压波动。为了抑制直流电压波动,在网侧变流器控制中加入了电流前馈控制器,其原理在于把机侧有功电流分量引入网侧有功电流分量控制中,如图1所示。其控制方程为:
(4)


2 直驱风电机组的并网自同步和惯量支撑分析
2.1 直驱风电机组的并网自同步
在直驱风电机组的网侧变流器控制中,直流电压控制器利用直流电容动态实现并网自同步。考虑到交流电压/电流控制器的响应速度较快[24],在分析并网同步时忽略交流电压电流控制器的动态从而简化分析。
直流电容的动态方程为:
(5)
式(5)可以进一步写成:
(6)
将式(6)代入式(2)中得到:
(7)
由于并网同步主要与风机输出电压的相角θ相关联[24],所以在此忽略直流电压的偏差以简化并网自同步分析。则式(7)可以进一步写成:
(8)
对比同步发电机的转子动态方程可以看出,KJCDC/2对应于同步发电机的惯量时间常数,KDCDC/2对应于同步发电机的电气阻尼系数,PWT对应于同步发电机的原动机输出功率,Pg对应于同步发电机的电磁功率输出,ω对应于同步发电机的转子转速。
因此,式(2)中的直流电压控制器可使网侧变流器模拟同步发电机转子动态方程,如图2所示。可以看出,直驱风电机组输出电压的相角(θ=ω/s)主要由直流电压控制器决定,而输出电压的幅值E则由无功—电压下垂控制器决定。因此,直驱风电机组可以等效成一个可控电压源,并且其输出电压相角和幅值分别来自于直流电压控制器和无功—电压下垂控制器,其等效模型如图2所示。

图2 并网自同步等效模型Fig.2 Equivalent model of grid-connected self-synchronization

2.2 直驱风电机组的惯量支撑
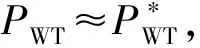
(9)
考虑到fg=2πω,将式(9)代入式(8)中可得:
PMPPT-Pg
(10)
对比式(10)与式(8)可以看出,在加入虚拟惯量控制后,直驱风电机组的等效虚拟惯量增大了2πKin,同时等效同步发电机的原动机输出功率由PWT变成了PMPPT,说明直驱风电机组中用来提供有功支撑的储能包括了在PMPPT与Pg之间的桨叶旋转储能和直流电容储能,并且通过调节Kin与KJ的大小可以灵活地控制这两种储能参与系统虚拟惯量支撑的比重。
在直驱风电机组中,考虑到直流电容储能远小于其存储的桨叶旋转动能,因此选择桨叶中的旋转储能作为主要的虚拟惯量模拟来源,并且在虚拟惯量协调控制中利用了电流前馈控制来减小直流电压的波动,从而进一步减小了直流电容储能在虚拟惯量模拟中的比重。综上,在虚拟惯量协调控制策略中,网侧虚拟同步控制实现了并网自同步,而机侧虚拟惯量控制主要实现直驱风电机组的惯量模拟,从而使得直驱风电机组既能够适应弱电网的运行条件,也能够将桨叶中的旋转储能为电网提供频率支撑。
值得一提的是,从式(9)中可以看出,在电网频率跌落的暂态过程中,风机的有功功率输出的参考值会暂时增加,进而释放风机转子中的动能为电网提供频率支撑,当暂态过程结束时,即dfg/dt=0,风机的转子转速将恢复到正常运行状态,因此虚拟惯量控制主要用于减缓系统暂态过程中频率的快速变化。同时,在虚拟惯量协调控制策略的机侧控制中也可以加入有功—频率下垂控制,此时直驱风电机组将能够在电网频率跌落时为电网持续提供有功功率支撑[25],本文限于篇幅不再讨论。
3 直驱风电机组小信号分析
3.1 直驱风电机组的系统闭环传递函数
本节将通过直驱风电机组的系统闭环传递函数分析其动态特性。考虑到已有很多文献研究了永磁直驱风电机组的小信号模型[11,26],可以根据小信号模型进一步得到直驱风电机组的功率传输闭环传递函数为(详细推导见附录A):
(11)
通过式(11)可以分析直驱风电机组系统在不同控制参数和电网条件下的动态特性。
3.2 直驱风电机组的动态性能及影响因素
为了分析电流前馈控制器对直流电压波动的抑制效果,图3(a)给出了由式(11)得出的在不同前馈系数KF下系统的闭环传递函数波特图。其中电网短路比SCR为5,虚拟惯量常数为Kin=3,且前馈系数KF从0增加到0.9。可以看出,当KF=0时,幅频曲线存在一个较大的谐振峰值,并且随着KF的增大,该谐振峰值逐渐减小,说明了增大KF能够改善有功功率的跟踪特性,进而减小暂态过程中PWT与Pg之间的偏差量,从而达到抑制直流电压波动的效果。
为了分析电流前馈控制器对直驱风电机组系统稳定性的影响,图3(b)给出了系统在不同前馈系数KF下的特征值轨迹。可以看出,在前馈系数KF从0增大到0.9的过程中,特征值3和4的实数部分减小,虚数部分基本保持不变,即这两个共轭特征值的频率基本不变,保持在6 Hz左右,而阻尼比增大。在引入电流前馈控制器后所有特征值均在左半平面,并且特征值3和4的阻尼增大,说明直驱风电机组的系统稳定裕度变大。同时,与图3(a)的有功功率波特图对比可知,由于当前馈系数KF较小时,图3(b)中的特征值3和4的阻尼较小,系统响应会在特征值3和4的频率下存在较大过冲,反映在图3(a)的幅频曲线中即为在该频率(6 Hz左右)下存在较大的谐振峰值,并且随着KF增大,特征值的阻尼增大,因此谐振峰值减小。
为了分析电网强度对风机系统动态特性的影响,图3(c)给出了在不同电网短路比SCR下的系统闭环传递函数波特图,且其中KF=0.9,Kin=3。从图3(c)中可以看出,随着电网短路比从5减小到1,系统的带宽从10.30 Hz减小到3.45 Hz。因此,当直驱风电机组接入弱电网时,风机系统的响应速度会变慢,但是可以看出在弱电网下,甚至SCR为1时,直驱风电机组的动态性能仍在可接受范围内,在该带宽范围内,直驱风电机组能够保持小干扰稳定性并且输出有功功率能在较短时间内跟踪上有功功率参考值。
为了分析不同电网短路比对直驱风电机组系统稳定性的影响,图3(d)给出了根据式(11)得到的系统在不同短路比下的特征值轨迹。可以看出,在电网短路比从5减小到1的过程中,特征值3和4的虚部减小,说明特征值3和4的频率在逐渐减小。由于在SCR为1时,所有特征值均位于左半平面,因此系统能够保持小干扰稳定。值得一提的是,式(8)中ωg由附加锁相环得到,附加锁相环只用于检测电网稳态频率,并不用于实现电网同步,对系统稳定性影响不大,因此在弱电网下即使锁相环动态性能变差,系统也能够保持稳定。(具体锁相环参数的影响分析见附录B)。
最后,进一步分析所提出的控制策略中虚拟惯量常数Kin对系统动态性能的影响。下面选取电网频率的微分量df/dt作为风机系统模型式(11)的输入信号,输出信号仍为网侧变流器的有功功率输出Pg。由此可以得到从df/dt到Pg闭环传递函数的波特图,如图3(e)所示。从图3(e)中可以看出,在SCR为5并且KF=0.9的条件下,随着虚拟惯量常数Kin从1增加到20,风机有功输出的增益逐渐增加,说明增加Kin可以提高直驱风电机组有功功率对电网频率波动的响应程度,从而提高风机对电网的功率支撑能力。

图3 直驱风电机组闭环波特图及特征值轨迹Fig.3 Bode diagram and loci of system eigenvalues for PMSG-based wind turbines
4 仿真与分析
4.1 单台直驱风电机组并网系统仿真分析
为了验证本文提出的虚拟惯量协调控制策略的有效性,本节针对图1所示的永磁直驱风电机组在MATLAB/Simulink中进行了电磁暂态仿真。其中主要系统参数如下:额定线电压Vnom=690 V,额定容量Pnom=1.5 MW,额定频率fnom=50 Hz,永磁直驱电机的dq轴电感Ld=Lq=1.387(标幺值),永磁直驱电机的惯量时间常数Ta=10.459 s,永磁直驱电机极对数P=48,直流电容CDC=0.12(标幺值),其他参数见附录C。
首先,为了验证虚拟惯量控制对直驱风电机组系统动态性能的影响,假设在t=1 s时电网频率由50 Hz跌落至49.8 Hz,此时不同虚拟惯量常数Kin下的直驱风电机组时域响应如图4(a)所示。可以看出,随着Kin的增加,直驱风电机组输出有功功率波动幅度变大,说明直驱风电机组能够响应电网频率波动,为电网提供惯量支撑,并且通过调节Kin可以灵活地控制直驱风电机组虚拟惯量的大小,从而为电网提供不同程度的有功功率支撑。同时,从图4(a)中可以看出,在暂态过程中,直驱风电机组有功功率的波动会使得直流电容两侧功率不平衡,进而导致直流电压波动。
为了验证电流前馈控制对直流电压波动的抑制效果,图4(b)给出了同样电网频率跌落的情况下,应用不同前馈系数KF时的直驱风电机组时域响应。可以看出,随着KF的增大,直流电压波动逐渐减小,并且t=1 s之后有功功率Pg的第一个峰值变化很小,说明电流前馈控制能够有效地抑制直流电压的波动,且同时可以维持直驱风电机组在频率跌落时为电网提供有功功率支撑的能力。
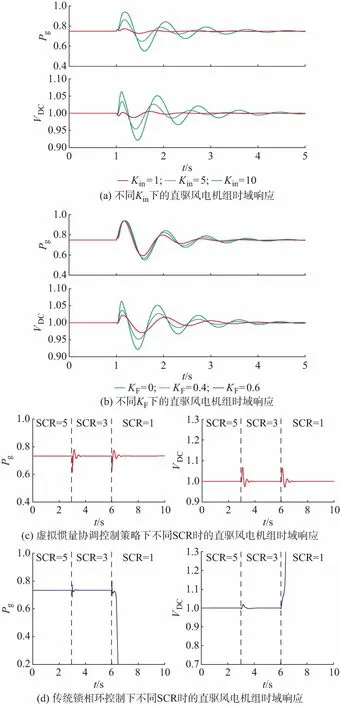
图4 直驱风电机组时域响应Fig.4 Time-domain responses of PMSG-based wind turbines
最后,为了验证直驱风电机组接入弱电网时的动态特性,假设由于电网拓扑变化导致系统短路比SCR在t=3 s时从5减小到3,再在t=6 s时从3减小到1,分别仿真得到在虚拟惯量协调控制策略和传统锁相环控制下的永磁直驱风电机组的时域响应,如图4(c)和(d)所示。对比图4(c)和(d)可以看出,在虚拟惯量协调控制策略下,永磁直驱风电机组在弱电网中具有良好的动态性能,甚至在SCR为1时也能保持稳定,而传统锁相环控制下的永磁直驱风电机组在SCR为1时输出有功和直流电压发散,风机系统失去稳定性。通过对比可以看出,本文所提出的虚拟惯量协调控制策略相较于传统锁相环控制在弱网下具有更好的动态性能和稳定性。
4.2 两区四机系统仿真分析
4.1节通过单机无穷大系统,验证了本文所提出的控制策略对电网频率的响应特性。本节为了更直观地反映该控制策略在实际电网频率波动时的频率支撑效果及电网频率的变化过程,针对永磁直驱风电机组接入两区四机的电网系统做进一步仿真分析。两区四机系统的电路结构如图5(a)所示,其中SG1,SG2,SG3,SG4分别代表4个同步发电机组,每台同步发电机输出有功功率为0.5(标幺值),永磁直驱风电场从母线B1接入电网系统,其输出有功功率为0.75(标幺值)。
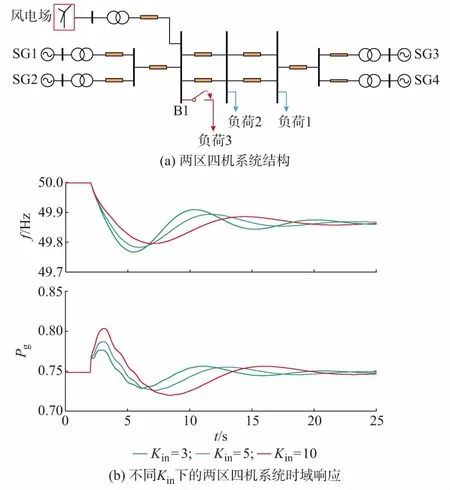
图5 两区四机系统结构及其时域响应Fig.5 Architecture of two-area four-machine power system and its time-domain responses
通过在母线B1上投切负荷3使得系统频率产生波动,从而研究频率波动时风电机组的响应过程和系统频率的变化过程。图5(b)给出了在不同虚拟惯量常数Kin下,系统在t=2 s时投入负荷3的电网频率和永磁直驱风电机组输出有功功率的时域响应曲线。从图5(b)中可以看出,在投入负荷3后系统的频率跌落,永磁直驱风电机组的输出功率迅速增加。同时随着虚拟惯量常数Kin的增加,风电机组输出功率的峰值增大,因此风电机组能够提供更多的功率用于支撑系统频率,使得电网频率跌落的谷值增大且下降斜率减小,说明增大Kin能够使风电机组在频率跌落时输出更多的有功功率,从而减缓电网频率的波动。
5 结语
针对永磁直驱风电机组提出了一种虚拟惯量协调控制策略,该策略在机侧变流器控制中引入虚拟惯量模拟,在网侧变流器控制中引入虚拟同步控制实现风机自同步。研究表明,虚拟惯量控制能使直驱风电机组能够在电网频率波动时利用储存的旋转动能为系统提供有功功率支撑,网侧的虚拟同步控制能够利用直流电容动态实现直驱风电机组与电网的同步。未来将研究该协调控制策略时风电机组在大干扰下的动态特性及其稳定性提升方法。
本文得到浙江省电力公司科技项目“含高比例可再生能源的系统振荡风险分析方法及应用研究”资助,特此致谢!
附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。
[1] 袁小明,程时杰,文劲宇.储能技术在解决大规模风电并网问题中的应用前景分析[J].电力系统自动化,2013,37(1):14-18.
YUAN Xiaoming, CHENG Shijie, WEN Jinyu. Prospects analysis of energy storage application in grid integration of large-scale wind power[J]. Automation of Electric Power Systems, 2013, 37(1): 14-18.
[2] HUANG L, XIN H, ZHANG L, et al. synchronization and frequency regulation of DFIG-based wind turbine generators with synchronized control[J]. IEEE Transactions on Energy Conversion, 2017, 31(3): 1251-1262.
[3] MORREN J, DE HAAN S W H, KLING W L, et al. Wind turbines emulating inertia and supporting primary frequency control[J]. IEEE Transactions on Power Systems, 2006, 21(1): 433-434.
[4] 黄林彬,辛焕海,黄伟,等.含虚拟惯量的电力系统频率响应特性定量分析方法[J].电力系统自动化,2018,42(8):31-38.DOI:10.7500/AEPS20170605010.
HUANG Linbin, XIN Huanhai, HUANG Wei, et al. Quantified analysis method of frequency respone characteristics for power systems with virtual inertia[J]. Automation of Electric Power Systems, 2018, 42(8): 31-38. DOI: 10.7500/AEPS20170605010.
[5] YE Hua, PEI Wei, QI Zhiping. Analytical modeling of inertial and droop responses from a wind farm for short-term frequency regulation in power systems[J]. IEEE Transactions on Power Systems, 2016, 31(5): 3414-3423.
[6] MAURICIO J M, MARANO A, EXPOSITO A G, et al. Frequency regulation contribution through variable-speed wind energy conversion systems[J]. IEEE Transactions on Power Systems, 2009, 24(1): 173-180.
[7] WANG Yi, MENG Jianhui, ZHANG Xiangyu, et al. Control of PMSG-based wind turbines for system inertial response and power oscillation damping[J]. IEEE Transactions on Sustainable Energy, 2015, 6(2): 565-574.
[8] 刘彬彬,杨健维,廖凯,等.基于转子动能控制的双馈风电机组频率控制改进方案[J].电力系统自动化,2016,40(16):17-22.DOI:10.7500/AEPS20150930009.
LIU Binbin, YANG Jianwei, LIAO Kai, et al. Improved frequency control strategy for DFIG-based wind turbines based on rotor kinetic energy control[J]. Automation of Electric Power Systems, 2016, 40(16): 17-22. DOI: 10.7500/AEPS20150930009.
[9] WANG Ye, DELILLE G, BAYEM H, et al. High wind power penetration in isolated power systems—assessment of wind inertial and primary frequency responses[J]. IEEE Transactions on Power Systems, 2013, 28(3): 2412-2420.
[10] 田新首,王伟胜,迟永宁,等.基于双馈风电机组有效储能的变参数虚拟惯量控制[J].电力系统自动化,2015,39(5):20-26.DOI:10.7500/AEPS20140320007.
TIAN Xinshou, WANG Weisheng, CHI Yongning, et al. Variable parameter virtual inertia control based on effective energy storage of DFIG-based wind turbines[J]. Automation of Electric Power Systems, 2015, 39(5): 20-26. DOI: 10.7500/AEPS20140320007.
[11] HU Jiabing, HU Qi, WANG Bo, et al. Small signal instability of PLL-synchronized type-4 wind turbines connected to high-impedance AC grid during LVRT[J]. IEEE Transactions on Energy Conversion, 2016, 31(4): 1676-1687.
[12] DRIESEN J, VISSCHER K. Virtual synchronous generators[C]// IEEE Power Energy Society General Meeting—Conversion and Delivery of Electrical Energy in the 21st Century, July 24-28, 2008, Pittsburgh, PA, USA: 3p.
[13] BECK P H, HESSE R. Virtual synchronous machine[C]// 9th International Conference on Electrical Power Quality and Utilization, October 9-11, 2007, Barcelona, Spain: 6p.
[14] ZHONG Qingchang, WEISS G. Synchronverters: inverters that mimic synchronous generators[J]. IEEE Transactions on Industrial Electronics, 2011, 58(4): 1259-1267.
[15] HUANG Linbin, XIN Huanhai, WANG Zhen, et al. A virtual synchronous control for voltage-source converters utilizing dynamics of DC-link capacitor to realize self-synchronization[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2017, 5(4): 1565-1577.
[16] WANG Shuo, HU Jiabing, YUAN Xiaoming. Virtual synchronous control for grid-connected DFIG-Based wind turbines[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2015, 3(4): 932-944.
[17] WANG Shuo, HU Jiabing, YUAN Xiaoming. On inertia dynamics of virtual-synchronous-controlled DFIG-based wind turbines[J]. IEEE Transactions on Energy Conversion, 2015, 30(4): 1691-1702.
[18] D’ARCO S, SUUL J A. Equivalence of virtual synchronous machines and frequency-droops for converter-based microgrids[J]. IEEE Transactions on Smart Grid, 2014, 5(1): 394-395.
[19] BLAABJERG F, TEODORESCU R, LISERRE M, et al. Overview of control and grid synchronization for distributed power Generation systems[J]. IEEE Transactions on Industrial Electronics, 2006, 53(5): 1398-1409.
[20] 谢小荣,刘华坤,贺静波,等.直驱风机风电场与交流电网相互作用引发次同步振荡的机理与特性分析[J].中国电机工程学报,2016,36(9):2366-2372.
XIE Xiaorong, LIU Huakun, HE Jingbo, et al. Mechanism and characteristics of subsynchronous oscillation caused by the interaction between full-converter wind turbines and AC systems[J]. Proceedings of the CSEE, 2016, 36(9): 2366-2372.
[21] DARCO S, SUUL J A, FOSSO O B. A virtual synchronous machine implementation for distributed control of power converters in smart grids[J]. Electric Power System Research, 2015, 122(6): 180-197.
[22] WANG Jing, CHANG N C, FENG X A, et al. Design of a generalized control algorithm for parallel inverters for smooth microgrid transition operation[J]. IEEE Transactions on Industrial Electronics, 2015, 62(8): 4900-4914.
[23] YAO Jun, LI Hui, LIAO Yong, et al. An improved control strategy of limiting the dc-link voltage fluctuation for a doubly fed induction wind generator[J]. IEEE Transactions on Power Electronics, 2008, 23(3): 1205-1213.
[24] DORFLER F, BULLO F. Synchronization and transient stability in power networks and non-uniform Kuramoto oscillators[C]// 2010 American Control Conference, June 30-July 2, 2010, Baltimore, MD, USA: 930-937.
[25] 李立成,叶林.变风速下永磁直驱风电机组频率-转速协调控制策略[J].电力系统自动化,2011,35(17):26-31.
LI Licheng, YE Lin. Coordinated control of frequency and rotational speed for direct drive permanent magnet synchronous generator wind turbine at variable wind speeds[J]. Automation of Electric Power Systems, 2011, 35(17): 26-31.
[26] LI Yujun, XU Zhao, WONG K P. Advanced control strategies of PMSG-based wind turbines for system inertia support[J]. IEEE Transactions on Power Systems, 2017, 32(4): 3027-3037.
贺家发(1993—),男,硕士研究生,主要研究方向:新能源并网控制技术。
宋美艳(1987—),女,硕士,主要研究方向:机电一体化与风机并网控制技术。
兰 洲(1980—),男,高级工程师,主要研究方向:电力系统控制与规划。
辛焕海(1981—),男,通信作者,博士,教授,主要研究方向:电力系统稳定与新能源并网技术。E-mail: xinhh@zju.edu.cn

