浅谈初中数学解题技巧

陈黎丽

(浙江省宁海县潘天寿中学 315600)

初中数学的学习，从根本上讲就是学会解题.解题的过程不但是一个强化理论知识的过程，更需要掌握一定的解题技巧与规律.为此，笔者根据多年的数学教学经验，对初中数学解题策略提出几点可行性建议，用来提高初中数学学习效率.

一、找准切入点

初中数学定理、定义较多，问题也纷繁复杂，学生在学习和解题的时候容易受到定势思维的影响，这就限制了学生的解题思路.这时教师不但要将数学的基础理论教给学生，还应当在解题思路上给予学生正确的指导，帮助学生调整思路，根据老师的指导与引导，对题目重新进行认真的分析与理解，然后找到合适的切入点，来解决问题.

例如：在学习一元一次方程组时，有这样一道题：“某玩具厂有4条大型玩具生产线和5条小型玩具生产线，为了适应市场的需要，玩具厂决定转产生产火车模型.如果用1条大型玩具生产线和2条小型玩具生产线，每天可以生产105个火车模型，如果2条大型玩具生产线和3条小型玩具生产线同时开工，每天可以生产178个火车模型，那么，大型玩具生产线和小型玩具生产线每天各能生产多少个火车模型？”

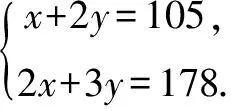
答: 每条大型玩具生产线每天生产火车模型41个， 每条小型玩具生产线每天生产火车模型32个.

这是一道较为经典的应用题，要通过学生对已知条件进行整合与分析，然后根据实际生产线的工作量来完成生产量，因此，审题的时候，可以提醒学生将两个未知的条件充分结合起来分析，提醒学生在设未知数的时候，将大型玩具生产线每天生产个数和小型玩具生产线每天生产个数分别设成x和y.

二、发挥想象力

面积是初中数学中常出现的问题，在面积定义与规律中，里面的数学思想内涵丰富，如果学生能够将题中包含的数学论证思想更明确地理出线索来，就可能会在其他的数学问题中利用面积的原理完成解题.在几何图形中，线段、角、面积、周长等的关系都是不可分割的，所以在面积的解题中不但涉及到面积，还会涉及到线段、角、周长等一系列问题.因此面积的探求等量关系的过程中还会有一些比例式的列出等多种类型的几何题.

例如：ABCD是一个矩形，而E、F是这个矩形AB、CD的中点，其中已知矩形EFDA与矩形ABCD相似，则矩形ABCD的宽与长之比为 .

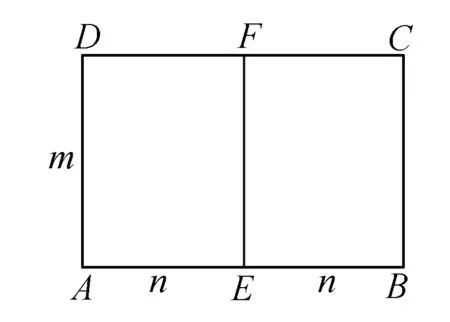
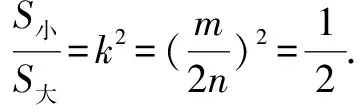
数学的解题并不是一道题只有一个解法.可能一道题多个解法，在解题的时候，教师可以利用不同的题型，开导学生产生更多的解题思路，扩展学生的思维.

三、利用特殊值求解

初中数学的虽然只是基础数学，但是从考核学生的综合素质能力来看，还是有一定的难度的.尤其是当前新课标要求，教师在教学的过程中要注意培养学生的素质，这在一定程度上加深了学生数学思维的培养，也就是说，很多教师在教学的时候会在数学问题上设置更多的问题来引导学生的思路，同时，很多教师基于对学生素质教育的考虑，将数学的难度提高了，使数学问题不再显得那么简单，使学生面对一些问题的时候感到无从下手.但是如果将这一数学问题在一定范围内研究它的特例，那么，问题就会迎刃而解.这就需要学生在思维上另辟蹊径，跳出一定的思维模式，很多问题就会解开了.

如在我们学习分解因式的时候，有这样的问题：将x2+2xy-8y2+2x+14y-3因式分解，这是一道二元多项式，这道题可以从多个角度来分析，如果从常规的思路来解这个问题的时候，可能要多走几道弯路，最后也会得到正确的答案，但是如果想帮助学生开拓思路，就需要从不同的角度来分析问题，这样才会引导学生开拓多方面的解题探索.现在解的思路就是从巧取特值的角度来解题的，将其中的一个未知数假定为0，就可以隐去这个未知数，这样可以将二元化为一元，利用这种简单的一元未知数求解的方式来求这个数，问题就解决了.

解假设y=0，就得到式子x2+2x-3=(x+3)(x-1)；假设x=0，则可以得到-8y2+14y-3=(-2y+3)(4y-1).在两次分解一次项系数时，我们分别得到了四个一次项的系数1、1、-2、4.而得到的1×4+(-2)×1时可以得到原来式子中的系数，这样只要能将前后综合起来就可以得到：

x2+2xy-8y2+2x+14y-3

=(x-2y+3)(x+4y-1).

这种利用特殊值来算这种二元式子的过程，也叫取零法.很多二元多项式都可以用这种方法来解决，有时利用这种方式可以帮助学生在解其他题的时候找到解题思路.但是在解题的时候需要注意，一个因式分两次分解，常数一定要相等，如本题中x+3与-2y+3中的3都相等，如果不相等，两次分解的因式就不会相等，综合后得到的得数也不会正确.

四、利用过渡法求解

在解初中数学的时候，不能只分析题中的明确已知的条件，还要将题全面分析，将其中包含的隐含条件也都分析出来，将数学中隐含的条件挖掘出来，并将这些条件加以综合利用，运用全面而深刻的理解与视角来解决问题.

例如，一个半圆的直径AB=30 cm，C和D分别为这个半圆上的三等分点，求弦AC、AD、CD围成图形的面积.

在这里需要求出的是一个不规则的图形.在这一条件下可以引导学生学会对半径的理解与利用.引导学生将两OC、OD两条线连接起来，将题目要求的不规则图形的面积连成规则的图形，这时就会将思路打开，学生也就会解了.

五、结论

初中数学是一门具有相当的科学性与基础性的学科，但是在解题的过程中一般都会因为思路的不同而有多种解法；有的数学题利用常规方法解决不了的，就要利用灵活性与技巧性来解决.教师的作用就是加强对学生的引导，帮助学生提高解题效率.

参考文献：

[1]刘鹏.浅谈初中数学解题技巧[J].初中生优秀作文,2015(22).

[2]寇海亮.浅谈初中数学解题技巧[J].数学学习与研究(教研版),2009(2).

[3]毛春来. 浅谈初中数学解题策略[J].学周刊：下旬,2014(04).