也谈添加平行线，证明线段比问题——兼与程志南老师商榷

胡育旭

(浙江省杭州市江干区杭州师范大学东城中学 310019)

本刊2016年第7期程志南老师的文章《探讨添线法构造“A”、“X”型相似图形解“燕尾”形问题》(下称文1)，笔者拜读后受益匪浅，被程志南老师严谨、认真、勤于思考的精神所感动.三角形相似的性质主要用于解决证明线段的比例以及求线段的长问题，但有些线段比例问题不能直接求得，往往需要通过添加平行线，构造相似三角形才得以解决.程志南老师在文1中分析了“A”、“X”型相似三角形的位置特征，并给出了过特殊分点添设平行线才能达到解题的目的，否则不能铺设由条件到结论的“路”.笔者认为这种方法并不是解这类“燕尾”形问题的本质，并且文1所提的“无用的平行辅助线”其实也能达到解题的目的，现作一些澄清，并给出此类问题的通法，不当之处，请同仁批评指正.

一、原题呈现，感悟解法

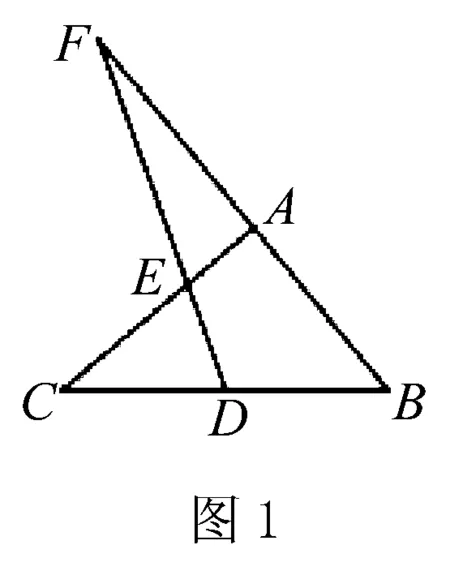
例1 如图1，已知直线FD与△ABC的边BC相交于D，与AC相交于E，与BA的延长线相交于F，且BD=CD，求证：AE·FB=EC·FA.

但程志南老师在文1中同时指出过点D、E、F这三个点所做平行线(图3)是无用的.笔者进一步的探究发现，实际上下面6幅图也是可以证明结论AE·FB=EC·FA的.

二、再添平行，新增六法

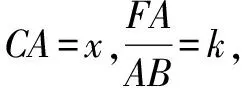
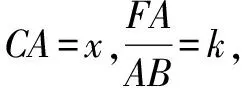
三、删去花絮，探究本质

根据上述方法，笔者发现文1中所提的“先根据比例关系寻找特殊分点，再过特殊分点作平行线”这种方法并不是本质的，实际上只要过图1中的任何一点作线段的平行线，利用这两个含有基本相似三角形的图形，都可以解决所证结论.解题方法的本质是：①直接利用上述两个基本的相似三角形得到线段比例式；②当不能直接利用相似三角形得到线段的比例式时，可以设其中某两条线段的比值为k，再利用相似三角形中的线段比值代换求得另一组线段比值也为k，从而得到结论.下面再举例说明.

例2 如图10，在△ABC中，D、E分别是边BC、AC上的点，且BD=DC，AE∶EC=1∶2，连结AD、BE交于F，求：AF∶FD的值.

仿照上述方法过点A、B、C、D、E、F分别作平行线，由于每个点可以作两条平行线，所以笔者得到16种证明方法，由于方法的类似，读者可以自己尝试解决.

四、学会解题，领会真谛

解题大师罗增儒教授指出“学会解题通常需要经历四个阶段：简单模仿→变式练习→自发领悟→自觉分析”.笔者在拜读文1时深受启发，简单模仿过点A、B、C添加平行线的方法，领悟到解法并深信过点D、E、F添加平行线也可以得到所证结论，本着这样的思考笔者得到了这类问题的通性通法，题目的本质所在，那么这个问题是否可以再进行一般化呢？如何变式练习呢？实际上问题可以进行如下改编：

利用文中笔者所提方法，显然可以求出结论.从特殊到一般是数学重要的思想方法，同时也是解题的重要指导思想，因此在教学的过程中笔者经常给学生创设问题变式的机会，让学生在学会解题，领会变中的不变，解题的方法本质所在.

参考文献：

[1]程志南.探讨添线法构造“A”、“X”型相似图形解“燕尾”形问题[J].数理化解题研究(初中版),2016(7):7-8.

[2]罗增儒,罗新兵.作为数学教育任务的数学解题[J].数学教育学报,2005(1):12-15.