基于搜索大数据的旅游需求自回归分布滞后模型预测研究

梁宗经，旷 芸

（1.广西师范大学计算机科学与信息工程学院，广西桂林541004；2.桂林师范高等专科学校，广西桂林541001）

一、引言与文献综述

旅游产业作为无烟工业，近几十年来，旅游产业持续快速发展。根据世界旅游权威机构预测，未来的旅游产业将成为世界第一大产业[1]。基于旅游产业在国民经济中的重要作用，研究产业的未来发展趋势、正确预测产业发展方向等问题，具有重要的现实意义。旅游需求是所有与旅游管理决策相关的基础，而旅游入境数则是最常用于指代旅游需求的指标，旅游入境数预测长期以来已成为旅游需求预测的热点问题[2]。

目前，国内外旅游入境数预测方法主要是采用定量研究方法，国内研究方法之一是采用传统的统计学模型，比如通过引入新的变量构建旅游目的地理论模型、应用回归方法预测旅游目的地游客数[3]，应用时间序列模型SARIMA、采用年度统计数据进行省级国际旅游需求预测[4]，采用ARFIMA模型进行我国旅游入境数预测[5]等；研究方法之二是应用人工智能理论[6-7]，已有的研究成果包括：结合BP神经网络和ARIMA建立组合模型，预测中国入境旅游数[8]，应用支持向量机理论预测旅游入境数，并与其它预测模型相比较，证明支持向量机模型是一种针对预测样本容量少、不确定因素多的旅游预测有效方法之一[9]。自2000年以来，国外研究在继续应用传统统计模型进行旅游需求预测的同时，许多新的技术及方法也应用到旅游预测中，其中就包括许多非线性理论模型，如神经网络、遗传算法、粗糙集理论、支持向量机等，通过对现有国外研究成果的分析，可以发现当前旅游预测的发展趋势是侧重现有模型的组合，从而适应当前旅游经济的发展多样性、提高预测精度[10]。

当前国内外旅游预测模型所用数据均是应用年度国家或省（州）官方统计数据，而统计年鉴数据均存在滞后性，不能实现实时预测，而信息技术高度发展的今天，互联网的应用已广泛应用于各行业，旅游行业是互联网应用最广泛、最有效的行业之一，现在互联网已被应用到旅游产业的各个环节，随着在线旅游信息的大量增加，搜索引擎已经成为了发现旅游相关信息及旅游规划的主要工具，通过搜索引擎，旅游管理者、从业人员能够发现潜在的旅游者[11]。搜索引擎查询数据包含了丰富的用户信息,并且这些数据是实时数据，为实时预测提供了宝贵的原始数据，搜索引擎指数可用于短期实时预测[12]，应用搜索引擎指数能够实现相关性指标的实时预测，克服传统预测模型采用年度、月度统计数据所具有滞后性的不足，从而实现实时预测。与此同时，应用搜索引擎指数进行相关性研究，可将搜索指数作为新的经济变量纳入预测模型，主要基于以下理由：（1）互联网的广泛应用为本研究提供了可能。当前世界上应用最广泛的搜索引擎为google搜索引擎，其为英文搜索，同时它也可以进行中文或其它语言的搜索，但主要搜索语言是英文，其次则是中文的搜索引擎百度搜索，百度搜索为纯中文搜索，以其特有的中文特征，成为华人地区的主要搜索引擎工具，此外，还有其它的搜索引擎，但因用户量少、市场占有率低，在全球搜索引擎市场中影响较少。google公司免费提供用户的搜索历史数据，这些海量数据为挖掘用户特征提供了第一手的原始数据，同样也为预测旅游入境数创造了实时跟踪的可能。（2）通过搜索引擎数据进行实时预测旅游需求，对于中国旅游业具有重要的现实意义。因为中国作为世界主要旅游目的地之一，以其丰富的自然资源与人文资源，实现实时预测将有助于旅游业的快速、健康发展。最早应用搜索指数进行预测应用的研究成果源于2008年发表于世界著名学术杂志《Nature》的一篇论文“Detecting influenza epidemics using search engine query data”，该论文首次开展google搜索指数与世界流感流行量的相关性研究，研究结果表明，搜索引擎指数能够实现实时监测[13]。自此以后，搜索指数已成功应用于流行疾病预测[14-15]、宏观经济指标预测[16-17]、商业周期预测[18]等。

综合国内外研究现状，目前应用搜索指数进行相关性研究主要集中于流行病预测、房地产研究、商品零售等，少有应用于旅游需求的研究报道，本文拟以美国入境中国香港地区的旅游入境数作为研究对象，通过构建自回归分布滞后模型，引入搜索引擎指数及其滞后变量，建立入境数预测模型进行实证预测分析。下面分三部分研究：理论简介，实证分析及结论。

二、理论简介

（一）搜索指数

搜索指数是由搜索引擎公司提供，该数据是根据特定搜索关键词的全球搜索量计算后得出。当前主要搜索指数为谷歌公司的搜索指数，又名Google trend。google trend是google公司推出的用于监测某关键词或某领域用户搜索的变化趋势指数，也称为google指数，数据源于全球范围的google用户，根据google公司提供的相关信息，google trend使用图表显示，横坐标为时间，纵坐标为google指数，图表上的数字表示在过去的某一时间跨度、某区域（国家、州、市）某个关键词的搜索历史记录，因原始数据已经过归一化处理，显示在纵坐标上的数字不是绝对搜索数，而是相对数字，即某时间跨度内对某个特定术语搜索数除以google的搜索总数，在数值表示上则定义为特定时间内最大搜索指数定义为100，而被查询的初始日期搜索指数定义为0[12]。自2004年以来，google公司还提供了众多的预定义搜索分类，分别为住房价格、旅游、电子产品等，该分类是指不需要用户输入搜索关键词，只需在google trend输入界面选择相关分类，即可得出相关的google指数值。

（二）自回归分布滞后模型

统计学分析方法一般为普通回归分析、单变量滞后模型、向量自回归和误差修正模型等，这些模型的应用都存在着诸多使用前提条件，比如，普通回归的应用前提是要求变量序列必须为平稳序列，单变量滞后模型只能分析单个变量滞后项对被解释变量的影响，而向量自回归与误差修正模型则与变量的排列次序紧密相关，次序不同计量结论也不同，从而影响了解释的不确实性，同时为了更好地了解大众关注与价格变动的关联性，需要同时考察二者的长期均衡关系，即变量间的协整关系，传统的协整关系分析，需要变量间为同阶单整，对于不是同价单整的变量协整关系则必须应用自回归分布滞后模型（即ARDL模型）[19]，ARDL模型可以分析不同价稳定变量的协整关系，但它的应用条件是变量可以是0阶或1阶稳定序列。在本文研究所使用的变量中，因变量数据序列不是同时一阶稳定序列，部分是稳定时间序列，部分变量数据时间序列为一阶稳定序列。因此，符合ARDL模型应用条件。基于此，在考虑数据序列的平稳性检验及增加计算结果的确定性前提上，本研究采用自回归分布滞后模型进行预测研究。

自回归分布滞后模型是一种计算变量间长期协整关系的定量分析方法，它能够避免传统协整关系检验需要同阶单整的前提条件，并能自动判定变量的滞后阶数，充分体现其性能的优越性。ARDL模型具有以下优点：（1）ARDL边界协整检验可有效应用于有限或少样本数据序列；（2）一旦确定滞后阶数，就可以应用ARDL进行边界检验的OLS回归分析；（3）无论数据序列是一价单整还是0价单整均可以采用ARDL进行协整分析；（4）应用ARDL模型能够确定回归结果的明确影响变量；（5）除可以进行长期协整分析外，还可以进行短期相关性分析。

根据ARDL的建模要求，具体步骤是首先进行数据序列的稳定性检验。一般采用ADF检验。其次，进行边界检验，最后分析长期协整关系及短期波动分析。二变量的ARDL的模型一般形式如公式所示[19-21]：

其中，公式（1）为双变量ADRL一般形式，公式（2）为长期协整关系公式。公式中的t表示时间，本文所用数据为月度数据，Yt表示入境数，Xt表示搜索指数，Yt-I、Yt-j和 Xt-I、Xt-j分别表示 Y 和X 的滞后 i期和 j期，a10、a20、a30为常数项，εt为误差项，p和q表示滞后价数，ln和△表示取对数和差分。

ARDL模型参数估计步骤：（1）平稳阶数检测。ARDL（m，n）模型要求建模数据序列必须为 0阶单整或1阶单整，但不要求同时同阶稳定。（2）模型参数估计。模型参数确定关键是二变量的滞后创数确定，滞后阶数根据计算结果的Akaike Information Criteria值决定，取该数值最小的模型滞后阶数。（3）边界检测。计算模型的F统计量，并与相应的误差数值表相对照，从而判断模型是否成立。（4）稳定性检验。进行（CUSUM）and the CUSUM of square（CUSUMSQ）检测[22]，绘制模型的CUSUM CUSUM of Squares图形，并根据图形决断模型的稳定性精度。（5）建立长期协整关系方程。采用已通过所有检验的ARDL模型进行预测分析，并分析预测结果。ARDL模型的协整检验主要是通过模型估计的F统计量作为检验标准，如果F统计量设定误差范围的边界值以内，则说明变量间存在长期协整关系，反之，则不存在长期协整关系。根据ARDL模型的理论要求，不同的变量数、不同单整阶数、不同的误差设定，均对不同的F参考值，实证应用只需要将计算结果的F统计量与相对的边界值相比较就可判断其协整性。

预测精度评测选用三个指标：MAE、MAPE和RMSE，其中MAE（平均绝对误差）：MAE通过计算预测值与真实值的绝对误差，并进行平均所得的误差估计指标，MAE的值越小，误差就越小，表示预测值与真实值的重合度越高。MAPE（平均绝对百分比误差），一般情况认为MAPE值小于10，则说明预测精度高，RMSE则是均方根误差。计算公式如下所示：

三、实证研究

本文选取美国至香港旅游入境人数作为研究对象，结合搜索指数研究入境数与搜索指数之间的关联性。选择香港作为旅游目的地的原因：（1）历史上很长时间里香港是中国与外国联系的主要联系港口，香港经济与内地经济紧密相联；（2）香港具有悠久的历史、文化底蕴以及丰富的旅游资源；（3）旅游业在香港占据重要的经济地位，旅游业贡献了香港GDP的5%、旅游从业人员占总就业的7.2%[23]。因此，研究以香港作为旅游目的地具有重要的现实意义。而以美国入境香港旅游人数作为分析数据，原因主要有：（1）根据香港旅游局的统计数据表明，美国为香港主要境外主要来源国之一；（2）英语为美国主要使用语言，谷歌公司为美国公司，在地区搜索中美国地区的谷歌指数数据是最为详细及完整，这有助于提高数据有效性。基于上述原因，本文以入境香港的美国人数、美国全境范围内针对香港的搜索指数作为研究对象，通过实证分析，研究实际旅游入境数与搜索指数的相关性，经过建模检验并预测，探讨搜索指数对实际旅游入境数的影响程度。

（一）原始数据

研究数据包括入境数据和搜索数据，其中入境数据取自香港旅游发展局公布的旅游统计数据（ 网 址 ：https：//www.discoverhongkong.com/cn-index.jsp），入境数据为月度数据，取值范围为2004年1月至2015年12月。搜索数据来源于谷歌趋势网站（网址：www.google.ca/google trends），因为谷歌指数界面除了设置用户搜索地外，还设置有搜索领域，其中就包括与旅游有关的子目录，本文选择其中的航空、景点和天气三个子目录的搜索数据，在本文中相应搜索指数分别以“flight”、“spot”和“weather”表示，搜索指数取值范围：2004年1月至2015年12月，数据类型为月度数据（自2017年1月1日起谷歌公司提供的搜索指数数据类型为月度数据，而之前提供的是星期数据）。下面的图1和图2分别为入境数据与搜索指数；表1和表2分别为原始数据统计描述及ADF平稳性检验表。

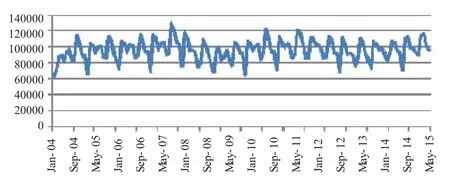
图1 2004年1月至2015年12月美国入境中国香港游客数折线图

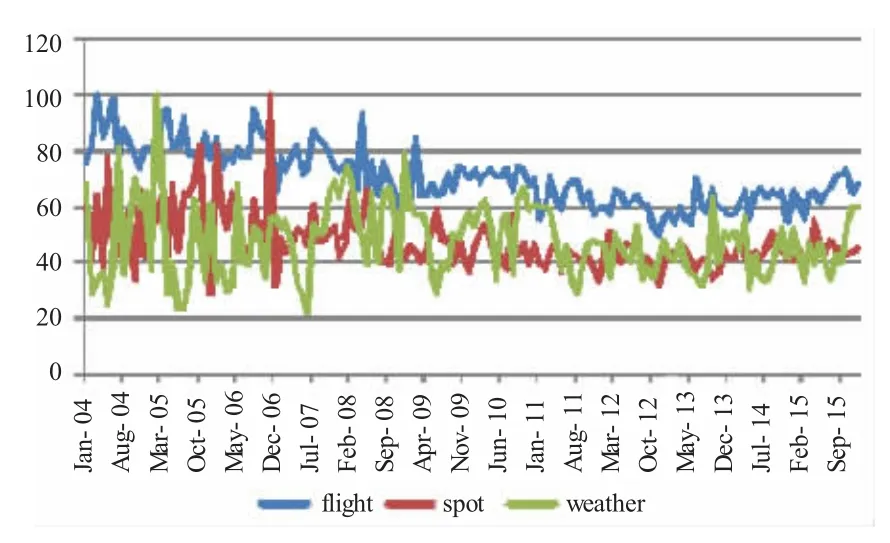
图2 2004年1月4日至2015年12月21日搜索指数（搜索地区为美国）折线图

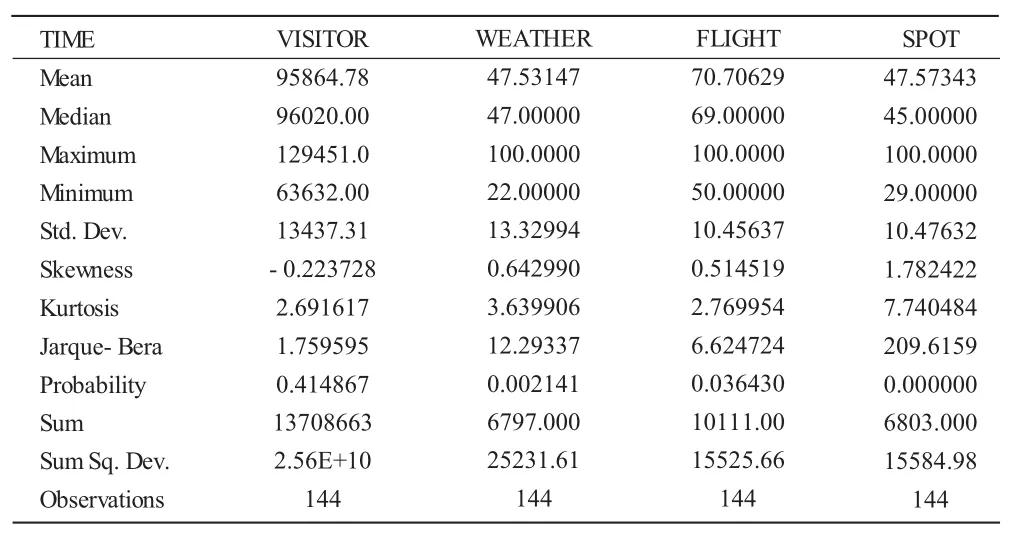
表1 原始数据统计描述（2004年1月至2015年12月）

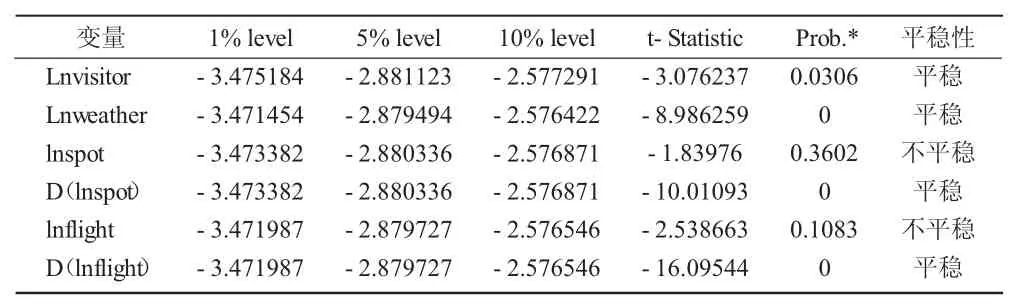
表2 ADF单位根检验表

从表2可以看出，入境人数（visitor）、天气搜索指数（weather）为平稳序列，即 0阶单整（即 I（0）），景点搜索指数（spot） 和航班搜索指数（flight）原始数列为不平稳时间序列，但它们的一阶差分序列为平稳序列，即1阶单整（即I（1）），因此时间序列数据符合ARDL的建模要求。

（二）模型估计

为了便于对比纳入搜索指数与否对预测精度的影响，本文分析采用ARMA与ARDL模型分别建模进行预测比较。其中建模数据的取值范围为时间：2004年1月至2014年12月，预测数据的取值范围为时间：2015年1月至2015年12月。

1.ARMA（p，q）模型。ARMA为自回归移动平均模型，ARMA模型的估计原理主要是使用时间序列数据的随机特性来描述其变化规律，即利用数据的过去值、当前值和随机滞后扰动项来建模估计，从而预测数据的未来值。经实际估算，ARMA（p，q）模型首先进行数列的稳定性检测，从表2中看出入境数列为平稳数列，符合ARMA（p，q）建模要求，第二步为模型识别，通过尝试不同的p，q值，通过比较不同的自相关系数（AC）和偏自相关系数（PAC）图，最后确定 ARMA（p，q）模型为ARMA（5，3），本文将此模型定义为模型 1。估计结果如表3所示。

表3 ARMA（5，3）模型估计结果

从估计结果可见，经过确定模型形式后，经过回归分析得出，模型的拟合度为R2=0.540105，调整R2=0.506178，F 统计量 =15.91977，Prob（F-statistic）=0.000000，这说明所建模型在统计意义上显著，且具有较好的拟合精度。接着进行预测分析，预测时间范围为2015年1月至2015年12月。预测数值及误差指标值如表7、表8所示，预测的三个误差指标值分别为MAE=0.094920、MAPE=0.825103、RMSE=0.111445。

2.ARDL模型。为了比较不同搜索关键词的预测精度，本文分别采集了关键词分别为“weather（即天气）”、“flight（航班）”和“spot（景点）”的搜索指数。下面分三组搜索指数进行ARDL模型估计，分别定义为模型2、模型3和模型4。根据ARDL模型的建模要求，分别进行系数估计、边界检测。

（1）系数估计。表4中，LNVI、LNWE、LNFL和LNSP分别表示入境数、天气搜索指数、航班搜索指数和景点搜索指数，表中括号内的数值表示滞后除数。从表4可以得出如下结论：①确定ARDL（p，q）模型的具体形式。ARDL模型p，q参数的确定采用SBC准则进行选择，计算结果分别为：模型 2 为 ARDL（12，0），模型 3 为 ARDL（12，0），模型4为ARDL（12，3）；②模型似合度比较。三个模型的拟合参数（即R2）分别为0.789、0.788和0.54，其中模型2的拟合程度最高，模型3次之，模型4最低；③系数符号解释。三个模型的因变量（即lnvi）均受其前期数值影响，但影响程度存在差异，模型2中的自变量（即LNWE）天气搜索量系数为-0.07，并且1%误差范围内在统计意义上显著，表示天气搜索量每变化一个单位，入境数即减少7%，即天气搜索量与入境数存在反向相关关系，表示游客对天气尤其关注，天气状况左右了游客的出境旅游；模型3的自变量（即LNFL）航空信息搜索量系数为0.12，并且1%误差范围内在统计意义上显著，表示航班信息搜索量每变化一个单位，入境数增加12%，即航班信息搜索量与入境数存在正向相关关系，表示游客对航班信息关注，充足的航班信息有助于游客出境旅游；模型4的自变量（即LNSP）旅游目的地景点搜索量系数为0.02，虽然该系数在5%误差的统计意义上不显著，但其滞后二阶变量 LNSP（-2）系数为0.11，在5%误差统计意义上显著，该结果说明，对于旅游目的地景点搜索量与入境数存在正向相关关系，表示游客对景点信息的关注有助于提高游客出境旅游的意愿。

表4 ARDL模型计量结果表

（2）边界检验。根据ARDL模型理论，表4中的模型估计必须是在因果变量存在协整关系的前提下得到，因此必须检验自变量之量是否存在协整关系。ARDL模型理论的协整关系是通过F统计量进行判断，经计数模型2至4的F边界检验结果如表5所示。

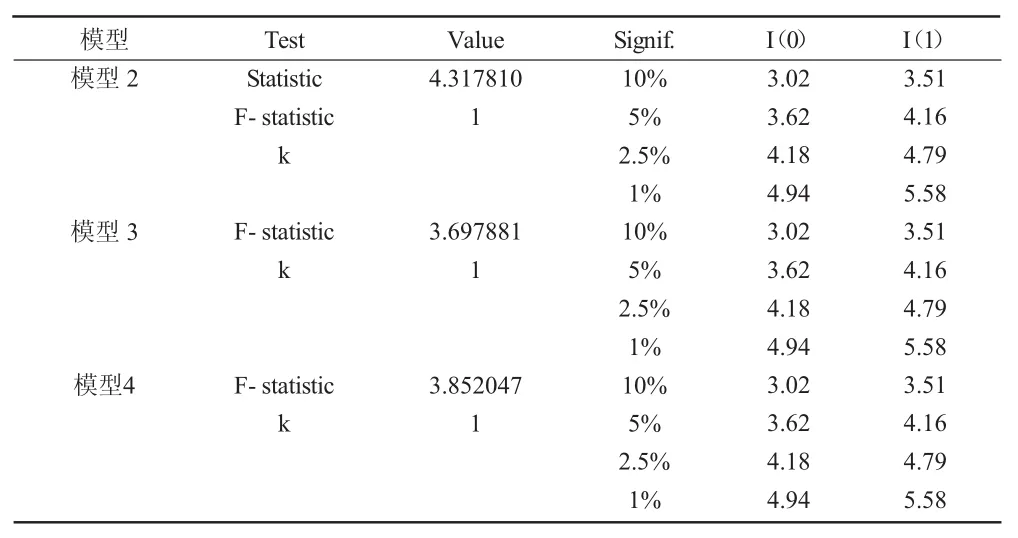
表5 F边界检验表

表5为模型F统计量计算结果，从表中可以看出三个模型的共同特点是K值为1，即表示三个模型均为1阶单整（即I（1））。模型2的F统计量为 4.317 810，比较 I（1）各概率误差值可以发现，模型5在5%显著性水平下存在协整关系，以此类推，模型3在10%显著性水平存在协整关系，模型4在10%显著性水平存在协整关系。因此，可以认为变量之间存在协整关系，同时也说明表4模型系数估计在统计意义上成立。

（3）协整检验。为了检验变量间的长期协整关系，在已证明变量间存在协整关系的基础上，需要进行模型的长期变量系数求解，根据计算长期系数为表6所示。

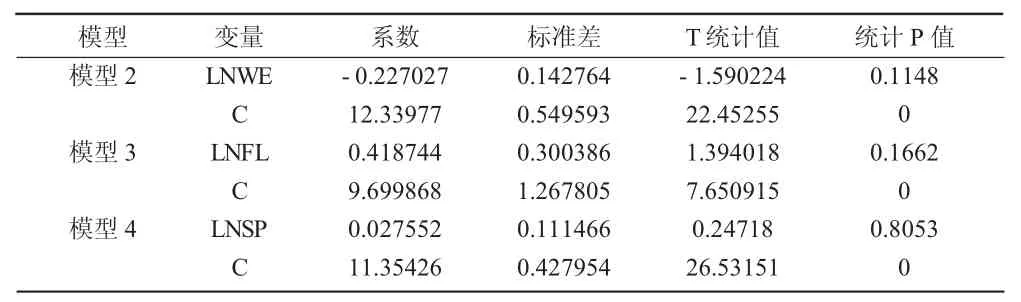
表6 长期协整关系系数估计表

从表6的长期系数表可以看出，模型2至模型4，各自变量系数与同期短期系数（见表4）具有相同的反馈作用，即对于模型2，游客对于天气的关注度与入境数成反比关系，即系数为负，而对于航班及景点的关注度则与入境数成正比关系，即相关系数为正。

（4）稳定检验。为了检验上述模型的稳定性，需要进行CUSUM、CSUMSQ检验[24]，即递归残差和递归残差和平方检验，检验结果如图3所示，其中红色虚线为5%误差范围，蓝色线为残差值。从图3可以看出，除入境数（lnvisitor）与天气搜索量（lnweather）的CUSM检验在2007年2月的残差值超过5%误差外，其它模型系数均通过了CUSUM、CSUMSQ检验。因此，可以认为所建ARDL模型成立，可以用于实际数据的预测分析。

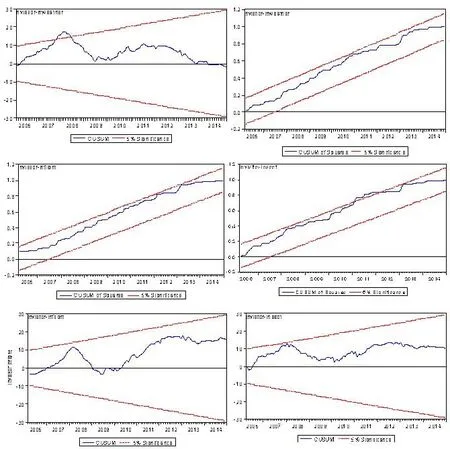
图3 CUSUM、CSUMSQ（即递归残差和递归残差和平方）检验图

（三）模型预测

经过上述对四个模型（ARMA和三个不同搜索指数的ARDL模型）、以用2015年1月至2015年12月的数据进行样本外预测，得到的预测值与实际值的对比表如表7所示，相应的误差指标值如表8所示。

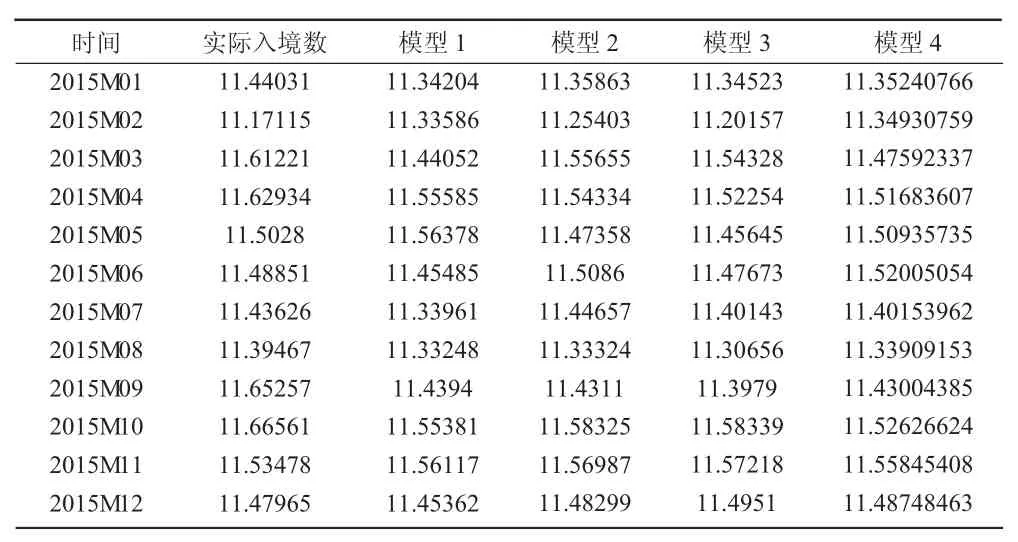
表7 模型预测表

误差指标分别采用平均绝对误差（MAE）、平均绝对百分比误差（MAPE）、均方根误差（RMSE），从表8可以看出，ARDL模型的误差指标值均小于ARMA模型，说明搜索指数是影响美国游客入境香港的原因之一，与此同时，发现预测误差最小的是基于天气搜索指数的ARDL模型（即模型2），该模型的三个误差值分别为0.064 128、0.556 066、0.084 777，均为四个模型中最小的，预测模型效果从好到差依次为模型2、模型3、模型4和模型1。

表8 模型预测精度指标值

四、结论

本文构建基于搜索指数的计量经济模型预测旅游需求。研究对象为美国入境香港旅游入境数，研究时间范围为2004年1月至2015年12月，数据类型为月度时间序列数据，采用的计量模型为自回归分布滞后模型（ARDL模型），为便于比较不同模型的预测精度，分别采用不包含搜索指数的ARMA模型（自回归移动平均模型）和包含搜索指数的ARDL模型（自回归分布滞后模型），而为了进一步了解不同搜索关键词对应的搜索指数对入境预测的差异，本文还选取了与旅游目的地紧密相关的三个不同关键词，并提取相应搜索指数数据。

实证结果表明：（1）搜索指数与入境人数存在长期协整关系。从经典时间序列理论可知，变量间的回归分析必须建立在同阶单整的基础上，如果不是同阶单整，则不可进行回归分析，但协整理论则可以解释不同阶单整变量间的数量关系。本文应用自回归分布滞后模型（即ARDL模型）分析旅游搜索指数与入境人数之间的数量关系，通过边界检验可知，在误差5%或10%范围内它们之间存在长期稳定的协整关系。（2）搜索指数与旅游需求存在相关性。实证结果显示，无论是短期还是长期范围内，搜索指数与入境数均存在相关性，通过构建四个预测模型验证了其定量关系，其中，包含搜索指数的ARDL模型预测精度均优于不包含搜索指数的自回归移动平均模型（即ARMA模型），而三个ARDL模型中，基于搜索关键词“天气”（即weather）的ARDL模型预测精度最高，其次为基于搜索关键词“航班”（即 flight）的ARDL模型，最后基于搜索关键词“景点”（即spot）为ARDL模型中预测精度最低。在旅游管理及决策的实际应用中，可以根据上述研究成果提出针对性的营销策略或管理办法。

旅游需求影响因素很多，除了与天气状况、旅游信息、旅游目的地景点吸引力、个人爱好等微观因素相关外，还与旅游来源国与目的地的汇率、来源国国民生产总值、来源国个人可支配收入等宏观经济状况有关，本文只是考虑了微观因素，没有纳入宏观经济变量，下一步的工作将结合宏观经济变量进行综合分析，以期更全面地了解影响旅游需求的影响因素。

【参考文献】

[1]第十届世界旅游旅行大会大盘点[EB/OL].[2017-07-01].http：//www.bjta.gov.cn/tsfwzt/wttc/wttctbgz/wttcymlm/342201.htm.

[2]Song H，Witt SF.Forecasting international tourist flows to Macau[J].Tourism Management，2006，27（2）：214-224.

[3]杨春宇，黄震方，毛卫东，2008.基于旅游学角度的游客量预测模型构建及其实证研究[J].生态经济（4）：124-127，132.

[4]张娜，佟连军，2012.基于SARIMA模型的黑龙江省冰雪旅游国际需求预测[J].资源开发与市场（7）：660-663.

[5]翁钢民，郑竹叶，刘洋，2009.我国入境旅游预测：基于ARFIMA模型的研究[J].商业研究（6）：1-4.

[6]纪成君，何建军，2010.国内旅游收入预测模型的比较[J].辽宁工程技术大学学报（自然科学版）（5）：990-993.

[7]杨立勋，殷书炉，2008.人工智能方法在旅游预测中的应用及评析[J].旅游学刊（9）：17-22.

[8]雷可为，陈瑛，2007.基于BP神经网络和ARIMA组合模型的中国入境游客量预测[J].旅游学刊（4）：20-25.

[9]李志龙，陈志钢，覃智勇，2010.基于支持向量机旅游需求预测[J].经济地理（12）：2122-2126.

[10]Song H，Li G.Tourism demand modelling and forecasting-A review of recent research[J].Tourism Management.2008，29（2）：203-220.

[11]Pan B，Litvin S，Goldman H.Real users，real trips，and real queries：an analysis of destination search on a search engine.In：Annual Conference ofTravel and TourismResearch Association（TTRA2006），Dublin，Ireland；2006；2006.

[12]Choi H，Varian H.Predicting the present with google trends[J].Economic Record.2012，88（s1）：2-9.

[13]Ginsberg J，Mohebbi MH，Patel RS et al.Detecting influenza epidemics using search engine query data[J].Nature，2008，457（7232）：1012-1014.

[14]Cook S，Conrad C，Fowlkes AL et al.Assessing Google Flu Trends Performance in the United States during the 2009 Influenza Virus A（H1N1）Pandemic[J].PLoS ONE，2011，6（8）：e23610.

[15]Ortiz JR，Zhou H，Shay DK et al.Monitoring Influenza Activity in the United States：A Comparison of Traditional Surveillance Systems with Google Flu Trends[J].PLoS ONE.2011，6（4）：e18687.

[16]Zhou RX，Wang XL，Tong GQ.Forecasting macroeconomy based on the term structure of credit spreads：evidence from China[J].Applied Economics Letters，2013，20（15）：1363-1367.

[17]Wu L，Brynjolfsson E.The future of prediction：How Google searches foreshadow housing prices and sales[D].Economics of Digitization.University of Chicago Press.2009.

[18]Iselin D，Siliverstovs B.Using Newspapers for Tracking the Business Cycle：A Comparative Study for Germany and Switzerland[J].KOF Swiss Economic Institute Working Paper，2013，（337）.

[19]Pesaran MH，Shin Y，Smith RJ.Bounds testing approaches to the analysis of level relationships[J].Journal of applied econometrics，2001，16（3）：289-326.

[20]Jalil A，Mahmood T，Idrees M.Tourism-growth nexus in Pakistan：Evidence from ARDL bounds tests[J].Economic Modelling，2013，35：185-191.

[21]Ozturk I，Acaravci A.Electricity consumption and real GDP causality nexus：Evidence from ARDL bounds testing approach for 11 MENA countries[J].Applied Energy，2011，88（8）：2885-2892.

[22]Trivedi P，Behera SR.The Macroeconomic Determinants Gold Prices in India：An ARDL Approach[J].Journal of International Economics（0976-0792），2012，3（2）.

[23]GovHK.AboutHK.Retrieved from GovHK：http：//www.gov.hk/en/about/abouthk/factsheets/docs/tourism.pdf[J].2017.

[24]Pahlavani M，Rahimi M.Sources of Inflation in Iran：An application of the ARDL Approach[J].International Journal of Applied Econometrics&Quantitative Studies，2009，9（5）：325-326.