局部锈蚀钢筋混凝土连续梁变形计算方法
夏成建
(中铁二院建筑工程设计研究院, 四川成都 610031)
钢筋锈蚀是导致钢筋混凝土连续梁承载能力及刚度损失的重要原因。钢筋锈蚀会从以下三个方面导致钢筋混凝土连续梁的承载能力及刚度损失:(1)钢筋的截面积减小;(2)钢筋的材料特性变化;(3)钢筋和混凝土间粘结性能变化。对于钢筋的截面积减小、钢筋的材料特性变化这两个方面,国内外已有较多的研究成果,并且得出了较为一致的结论[2-4],因此现在最需要研究的是钢筋和混凝土间粘结性能退化对钢筋混凝土梁变形的影响。对此问题,惠云玲等[5]提出根据GB 50010-2010(2015年版)《混凝土结构设计规范》(以下简称《设计规范》)计算钢筋混凝土梁的变形,并考虑锈蚀率引起的挠度增大系数;孙彬、牛狄涛、王庆霖[6]提出根据《设计规范》提供的钢筋混凝土梁刚度计算公式,利用梁“整体刚度退化系数”反映粘结退化对梁变形的影响;Ballim Y、Reid JC、Kemp AR[7]考虑了荷载大小对已发生锈蚀的钢筋混凝土梁刚度的影响,结论为荷载越大,锈蚀钢筋混凝土梁相对未锈蚀梁的变形越大;E.H.Khor等[8]利用概率分析方法,对锈蚀钢筋混凝土梁在可变荷载作用下的长期挠度变化进行了讨论。以荷载作用下节点曲率变化为基础,并在分步荷载作用后对截面尺寸、材料特性加以调整。以上研究大多未考虑局部锈蚀情况,且主要是通过实验数据拟合修正系数以计算锈蚀后钢筋混凝土梁的变形,由于实验条件的差别及控制参数的不同,不同文献的研究成果不尽相同,甚至有些差别较大。而且仅仅通过实验数据拟合无法真正揭示完好梁与局部锈蚀梁最主要的区别——在局部锈蚀范围内钢筋与混凝土间传递粘结应力的能力不同。因此,根据受拉区纵筋局部粘结退化简支梁的变形计算模型[1],本文提出了受拉区纵筋局部锈蚀连续梁的变形计算模型,力求从本质上揭示局部锈蚀对钢筋混凝土连续梁变形的影响机制。
1 研究范围和基本假定
1.1 研究范围
实际工程中钢筋混凝土梁跨高比一般处于8~14之间,为贴合实际工程,本文不考虑深受弯情况,将研究对象界定为跨高比大于5的连续梁。
1.2 基本假定
1.2.1 截面分析时材料的应力-应变模型
钢筋的应力-应变模型采用理想弹塑性模型[9],如下式:
当εs<εsy时,σs=Es×εs
当εs≥εsy时,σs=fy
(1)
混凝土的单轴受压应力-应变曲线采用曲线方程拟合[10],如下式:
x≤1:y=αax+(3-2αa)x2+(αa-2)x3
x>1:y=x/[αd(x-1)2+x]
(2)
式中:
x=ε/εc,y=σ/fc。
Es为钢筋的弹性模量;εs为钢筋应变;fy为钢筋的屈服应力;σs为钢筋的应力;εsy为钢筋的屈服应变。fc为混凝土的单轴抗压强度;αa、αd为混凝土的单轴受压应力-应变曲线上升及下降段参数,εc为混凝土的峰值压应变。以上参数取值均按文献[11]执行。
1.2.2 变形计算时材料的应力-应变模型
线弹性应力-应变模型属于材料力学及结构力学的基本假定,本文计算钢筋混凝土连续梁的变形时采用结构力学方法,材料应力-应变模型均按文献[11]取值。
1.2.3 其它基本假定
本文研究的钢筋混凝土连续梁应满足如下假定:
(1) 梁受拉纵筋锚固完好;
(2) 梁配筋满足《设计规范》要求;
(3) 混凝土抗拉强度为0;
(4) 荷载效应小于0.85Pu,其中Pu指构件极限承载能力(符合正常使用极限状态要求);
(5) 不考虑混凝土裂缝处骨料的咬合作用以及受拉区纵筋的销栓作用。
2 完好钢筋混凝土连续梁的变形计算模型
2.1 完好连续梁的定义
本文完好连续梁指满足本文全部假定且未发生局部锈蚀的钢筋混凝土连续梁,与本文局部锈蚀钢筋混凝土连续梁对应。
2.2 完好连续梁的变形计算模型
任意外荷载下,完好连续梁的受拉区裂缝分布及变形示意如图1。
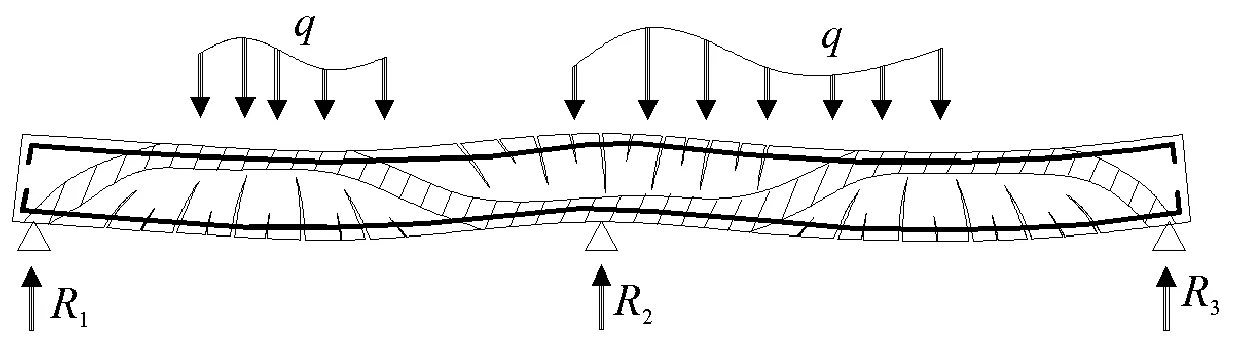
图1 完好连续梁裂缝分布及变形示意
上图的阴影路径示意了外荷载的主要传导路径。
根据文献[12],忽略纵筋的销栓作用后,完好连续梁受拉区纵筋仅承受轴向拉力作用。根据文献[13],通过钢筋与混凝土间的粘结作用,任两条相邻裂缝间的混凝土齿在受拉区纵筋位置受两侧纵筋的拉力差△F作用;相应混凝土齿根部承受△F引起的剪力及弯矩。根据文献[14],外荷载的作用下,梁阴影部分混凝土受压力及剪力作用。
根据以上分析,忽略受拉区纵筋的销栓作用后,梁受拉区纵筋仅受拉力作用,可用索单元(拉杆)模拟。阴影部分混凝土及任两条相邻裂缝间的混凝土齿均同时受轴力、剪力或弯矩的作用,均可用梁单元(分别令其为压杆和腹杆)模拟。为便于计算,假定腹杆轴线均与梁轴线垂直。鉴于水平拉杆与腹杆的连接节点仅传递混凝土齿两侧纵筋的拉力差△F,故该节点可定义为铰接;鉴于压杆与腹杆连接节点传递了△F及其引起的弯矩,故该节点可定义为刚接。按上述分析简化后,可用图2的完好连续梁的刚架模型模拟实际工程中的钢筋混凝土完好连续梁,且在任意外荷载的作用下,该模型各杆件的受力情况与实际完好连续梁相应部位的受力情况高度一致。

图2 完好连续梁的刚架模型
完好连续梁的刚架模型各参数的解释及确定方法如下:
d1、d2、d3指跨中或支座处相邻腹杆间的距离,按该跨平均相邻裂缝间宽度ls取值,ls按《设计规范》进行计算,各刚架相邻跨的分界点以反弯点界定。
h指刚架的高度,由相应梁截面受拉区纵筋及受压区混凝土间内力臂z决定。当外荷载接近构件承载能力时,z≈h0-x/2;当外荷载接近零时,z≈5h0/6;其它外荷载情况下,5h0/6 a1、a2、a3、a4指斜向压杆两端点之间的距离,参考文献[12],λ<2时,a=av;λ>=2时,a=2h;其中λ指各剪跨段的剪跨比,av指剪跨段长度。 根据《设计规范》,计算钢筋混凝土梁变形时可采用最小刚度法,故压杆的截面高度可按最不利截面上受压区混凝土的截面高度确定:当构件接近承载能力极限状态时,最不利截面受压区混凝土截面高度同截面中和轴高度xa,按《设计规范》进行计算;当外荷载为零时,取最不利截面受压区混凝土的截面高度为h0/2;其它外荷载情况压杆的截面高度均按线性插值计算;压杆的截面宽度同混凝土梁宽度b。 拉杆的截面同受拉区纵筋的截面。 腹杆的截面宽度同混凝土梁宽度b;腹杆的截面高度同相邻裂缝间混凝土的平均宽度ls。 将钢筋和混凝土的弹性模量输入按以上方法建立的完好连续梁刚架模型后,任意外荷载下完好连续梁的变形均可通过结构力学方法求得。 由于缺乏适当的模型基础,直接建立局部粘结退化钢筋混凝土连续梁的变形计算模型非常困难,为寻找突破口,本文先建立局部无粘结钢筋混凝土连续梁的变形计算模型。 对比完好钢筋混凝土连续梁和局部无粘结钢筋混凝土连续梁,局部无粘结范围内能否传递粘结应力是它们最重要的区别,此区别会影响图1中混凝土齿在与受拉区纵筋连接处能否受其两侧纵筋的拉力差△F作用,从而影响图2所示完好梁刚架模型中局部无粘结范围内腹杆的剪力是否被释放。鉴于以上因素,局部无粘结状态可通过向相应范围内腹杆下部添加链杆模拟。图3即是添加了链杆后的局部无粘结连续梁刚架模型。该模型其余各参数的确定方法均按本文2.2节执行。 将钢筋和混凝土的弹性模量输入按以上方法建立局部无粘结连续梁刚架模型后,任意外荷载下局部无粘结连续梁的变形均可通过结构力学方法求得。 图3 局部无粘结连续梁的刚架模型 3.2.1 局部粘结退化钢筋混凝土连续梁的变形计算模型 对于受拉纵筋局部锈蚀程度不严重的情况,钢筋锈蚀量的增加会引起锈蚀后钢筋与混凝土间的粘结强度的增加[15]。分别定义未锈蚀情况和局部锈蚀情况下钢筋与混凝土间的粘结强度为τu0(x)、τu(x),则当τu(x)≥τu0(x)时,根据《设计规范》即可求得此类局部粘结退化钢筋混凝土连续梁的变形。 当τu(x)<τu0(x)时,由于剪跨段弯矩的变化速度会随着剪跨段剪力的增大而增大,相应的受拉区纵筋拉力及钢筋与混凝土之间需传递的粘结应力亦按此原则变化,故粘结破坏最易发生在剪力最大段,故取剪力最大段分析。任意外荷载下,定义剪力最大段两端截面受拉纵筋的内力分别为Fs1和Fs2,Fs1和Fs2均可按本文3.2.2节方法求得。 如果R≥S,表明局部粘结退化后,相应范围内钢筋与混凝土间的残余粘结强度依然能满足钢筋与混凝土间粘结应力的传递,则根据《设计规范》即可求得此类局部粘结退化钢筋混凝土连续梁的变形。 当受拉区纵筋锈蚀量较大导致R (3) 上式中:τucr(x)指临界粘结强度,定义R=S后,通过下式(4)即可求得。如果分析区域不只一段,则τucr(x)取各段计算值的最大值: τucr(x)=2×(Fsb2-Fsb1)/d1/π/d/n (4) 3.2.2 计算受拉纵筋内力Fs 假设该截面应变满足平截面假定且钢筋与混凝土间粘结完好,则该截面钢筋与混凝土的应变如图4所示。 图4 钢筋与混凝土截面应变分析 (5) 从而: (6) (7) 利用数值计算,设xa和εc为两个递增的变量,通过多重循环语句计算并以式(7)为判别条件,即可计算出上式中的εc和xa,进而计算出Fs。 (1)钢筋混凝土连续梁发生局部锈蚀后,当钢筋与混凝土间的残余粘结强度大于其临界粘结强度τucr(x)时,局部粘结退化不会对梁的变形产生影响。此时,根据《设计规范》,输入锈蚀后钢筋的实际截面面积以及锈蚀后钢筋的实际材料特性,即可计算出任意外荷载作用下局部锈蚀钢筋混凝土连续梁的变形。 (2)钢筋混凝土连续梁发生局部锈蚀后,当钢筋与混凝土间的残余粘结强度小于其临界粘结强度τucr(x)时,梁的变形会因为局部粘结退化而增大。此时,根据本文3.2节所建立的局部粘结退化钢筋混凝土连续梁的变形计算模型,输入锈蚀后钢筋的实际截面面积以及锈蚀后钢筋的实际材料特性,即可计算出任意外荷载作用下局部锈蚀钢筋混凝土连续梁的变形。 [1] 夏成建,宋晓冰. 局部粘结退化钢筋砼梁变形计算模型[J]. 四川建筑科学研究, 2012, 38(2): 108-112. [2] Lee H S, Noguchi T, Tomosawa F. FEM analysis for structural performance of deteriorated RC structures due to rebar corrosion[A]. Proceedings of the Second International Conference on Conrete Under Severe Conditions, Troms, Norway. 1998: 327-336. [3] Wang Xiaohui, Liu Xila. Modelling effects of corrosion on cover cracking and bond in reinforced concrete[J]. Magazine of Concrete Research, 2004, 56 (4): 191-199. [4] Rodriguez J, Ortega L M, Casal J. Load carrying capacity of concrete structures with corroded reinforcement[J]. Construction and Building Mater, 1997, 11(4): 239-248. [5] 惠云玲, 李荣, 林志伸, 等. 混凝土构件钢筋锈蚀前后性能试验研究[J]. 工业建筑, 1997, 27(6): 14-18. [6] 孙彬, 牛狄涛, 王庆霖. 锈蚀钢筋砼梁抗弯刚度分析与计算[J]. 建筑结构, 2004, 34(10) : 42-45. [7] Ballim Y, Reid JC, Kemp AR. Deflection of RC beams under simultaneous load and steel corrosion[J]. Magazine of Concrete Research, 2001, 53 (3): 171-181. [8] E.H.Khor, D.V.Rosowsky, M.G.Stewart. Probabilistic analysis of time-dependent deflections of RC flexural members. Computers & Structures, 2001, 79(16): 1461-1472. [9] Li Zhujing. Elementary Reinforced Concrete Design[M]. Peiking: Tsinghua university press, 2005: 22-23. [10] 过镇海, 时旭东. 钢筋砼原理和分析[M]. 北京: 清华大学出版社, 2003: 287-289. [11] GB 50010-2010(2015年版) 混凝土结构设计规范[S]. [12] Kotsovos M D, Pavlovic M N. Ultimate Limit-state Design of Concrete Structures: a new approach[M]. London: Thomas Telford Ltd., 1999: 56-68. [13] 王传志, 滕智明. 钢筋砼结构理论[M]. 北京: 中国建筑工业出版社, 1985: 180-182. [14] 蓝宗建, 梁书亭, 孟少平. 混凝土结构设计原理[M]. 南京: 东南大学出版社, 2002: 136-139. [15] Wang Xiaohui, Liu Xila. Modeling bond strength of corroded reinforcement without stirrups[J]. Cement and Concrete Research, 2004, 34(8): 1331-1339. [16] Kim W, White R N. Initiation of shear cracking in reinforced concrete beams with no web reinforcement [J]. ACI Structural Journal, 1991, 88 (3): 301-308. [17] 孙彬. 在役钢筋砼结构的性能退化与抗震性能评估[D]. 西安:西安建筑科技大学土木工程学院, 2006.3 局部粘结退化钢筋混凝土连续梁的变形计算模型
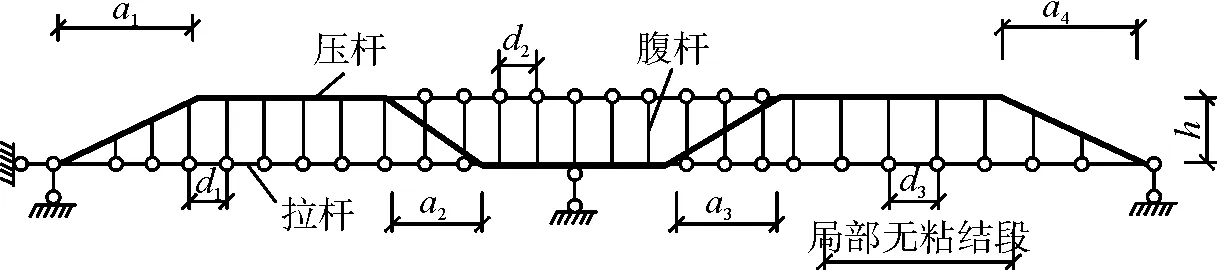
3.1 局部无粘结钢筋混凝土连续梁的变形计算模型
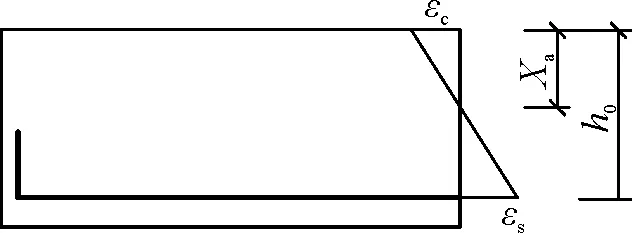
3.2 局部粘结退化钢筋混凝土连续梁的变形计算模型


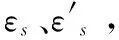
4 局部锈蚀钢筋混凝土连续梁变形计算方法

