路桥过渡段沥青路面平整度的评价方法

苏曼曼, 张洪亮

(1. 石家庄铁道大学 交通运输学院, 河北 石家庄 050043; 2. 长安大学 特殊地区公路工程教育部重点实验室, 陕西 西安 710064)

桥台与引道之间的差异沉降是引起路桥过渡段不平整的主要原因,不平整的桥头会影响行车的舒适性与安全性,加剧桥头损坏,增大维修费用.在路桥过渡段设计与施工中虽然采取诸多方法对该段路基进行加固与支撑[1-3],但差异沉降仍然不可避免.对桥头容许差异沉降的研究是预防跳车的关键,为确定容许差异沉降值,国内外对桥头乘坐舒适性进行了很多现场试验研究.对于不设搭板的路桥过渡段,文献[4]认为错台高度达到1.2 cm时会产生跳车;文献[5]认为当车辆以高于100 km·h-1的车速通过错台高度为2 cm的桥头时,会产生明显的跳车感觉;文献[6-7]认为错台高度低于1.5 cm时对行车舒适性无影响.当桥头设有搭板时,文献[4]认为搭板纵坡值低于0.5%时不影响乘车舒适性;文献[8]认为0.8%可作为简支跨桥梁搭板纵坡容许变化值;文献[9]通过现场试验提出高速公路桥头搭板容许纵坡变化值不宜大于0.5%.

综上可知,不同学者提出的容许差异沉降值并不一致,主要原因[10-12]如下: ① 桥头振动评价指标不合理、不一致,如果采用加速度加权均方根值作为评价指标,车辆经过桥头时振动波形系数较大,属于典型的瞬态振动,因此采用该值会低估振动的影响; ② 不同试验人员舒适性感受不同,容许差异沉降受试验人员主观影响较大;③ 现场试验时,试验车辆的车速难以准确控制.

鉴于此,有学者采用理论法进行了相关研究.文献[13]通过五自由度车辆模型研究了路桥过渡段的差异沉降.文献[14]通过三自由度车辆模型,研究车辆通过桥头的振动,并提出采用最大瞬态振动值(MTVV)作为桥头跳车的振动评价指标较为合理.但文献[14]未对MTVV进行分级,故如何对MTVV进行分级有待进一步研究.而且理论法建立车辆模型通常将车辆轮胎简化成一个阻尼为0的弹簧,忽略了实际轮胎阻尼对振动的影响;现有的三、五自由度车辆模型均无法考虑车辆的侧倾与转动,这与实际不符[15],有必要构建整车模型进行相关研究.笔者前期已构建整车模型,并对普通沥青路面平整度进行了研究,结果表明采用整车模型进行平整度的评价更合理[16].

为此,针对利用理论法与现场试验法研究路桥过渡段的缺陷,本研究提出采用整车模型仿真法对路桥过渡段平整度的振动舒适性进行研究.

1 人-车-路相互作用仿真

采用ISO 2631-1:1997《机械振动与冲击:人体暴露于全身振动的评价》提出的辅助评价方法中的最大瞬态振动值(MTVV)作为振动舒适性评价指标,进行路桥过渡段人体舒适性的评价.MTVV计算公式为

(1)

式中:aw(t)为瞬时频率加权加速度幅值,m·s-2;τ为持续平均积分时间,s;t为积分变量时间,s;t0为瞬时时间,s.

利用Carsim建立整车模型和路桥过渡段模型,进行人-车-路相互作用仿真.

1.1 整车车辆模型

采用桑塔纳3000作为仿真试验车,以Carsim软件中E-class车辆作为基础模型,通过设定轮胎、转向系和悬架等参数建立整车模型.车辆部分参数见表1.

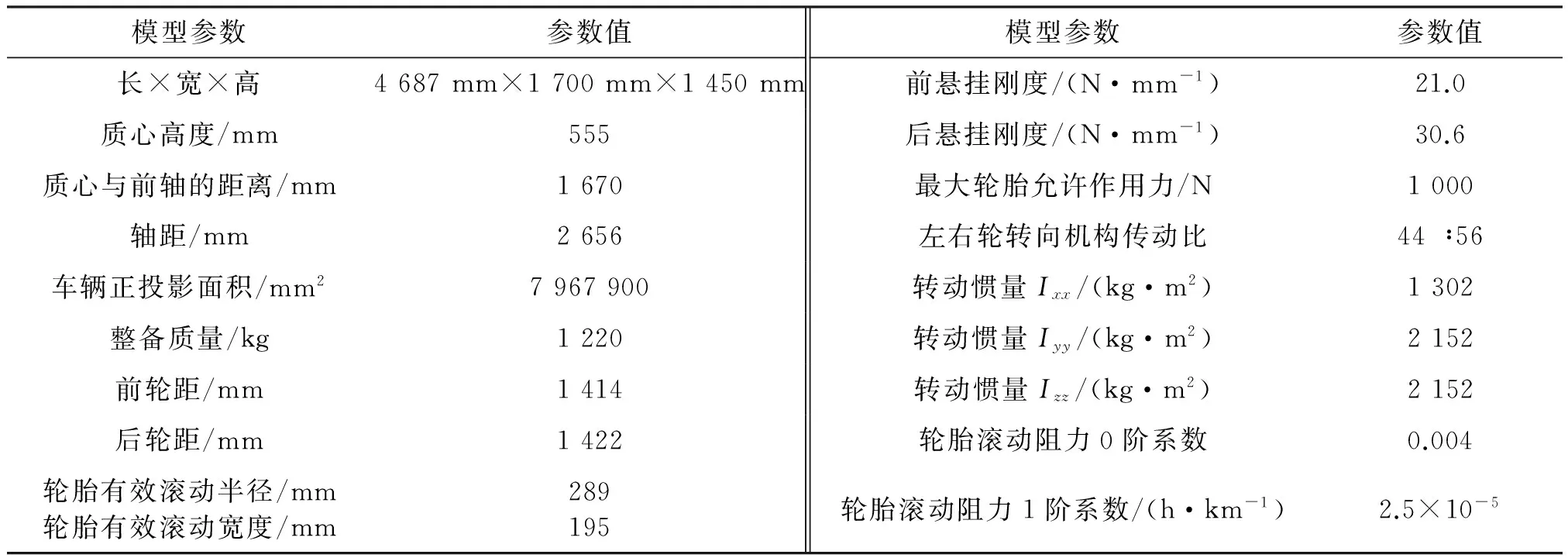
表1 车辆模型参数

1.2 路桥过渡段模型

① 设有搭板的路桥过渡段，选择6,8,10和12 m作为搭板长度进行模拟工况设计,每种搭板长度对应6个纵坡变化值,即0.001,0.002,0.004,0.006,0.008和0.010.② 不设搭板的路桥过渡段，选择错台台阶高度分别为1,2,3,4,5和6 cm.根据设定的路桥过渡段模拟工况,利用Carsim软件中道路模块建立道路模型.将加速度传感器设置于主驾座椅,调用不同工况建立的路桥过渡段道路文件,分别以60,80,100和120 km·h-1的车速对每个路桥过渡段工况进行人-车-路相互作用模拟仿真,如图1所示,并采集实时座椅加速度数据.

图1 人-车-路相互作用模拟仿真

图2为仿真车辆80 km·h-1车速通过搭板长度8 m、纵坡变化值0.6%的路桥过渡段的座椅垂向加速度数据.图3为台阶高度1 cm的路桥过渡段的座椅垂向加速度数据.

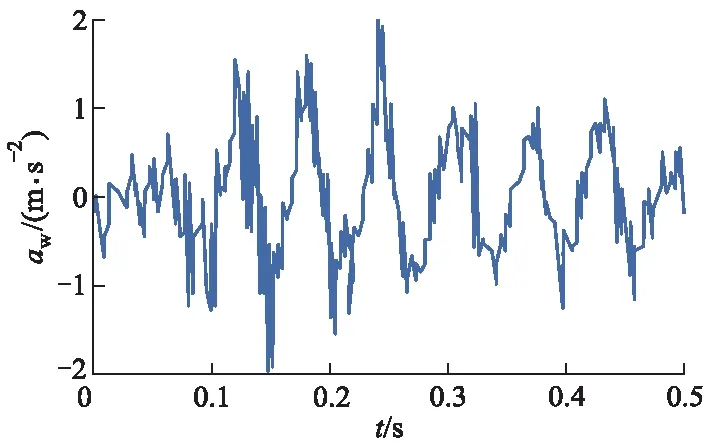
图2 搭板长度8 m、纵坡变化值0.6%工况模拟结果

图3 台阶高度为1 cm工况模拟结果

2 仿真结果分析

2.1 设有搭板的路桥过渡段

车辆驶过设有搭板的桥头时,瞬间振动时间t0为

(2)

式中:L为搭板长度,m;l为车辆轴距,m;v为车辆通过过渡段的车速,km·h-1.

根据不同工况下仿真得到的加速度数据,参照式(1)计算最大瞬态振动值MTVV,绘制MTVV变化曲线图，如图4-7所示,进而分析搭板长度、纵坡变化值和车速对MTVV的影响.

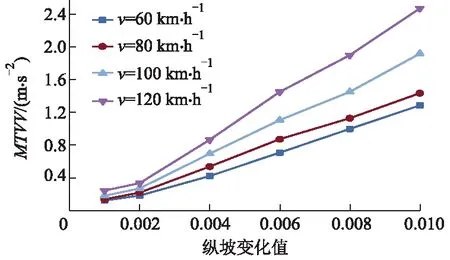
图4 L=6 m时MTVV变化规律

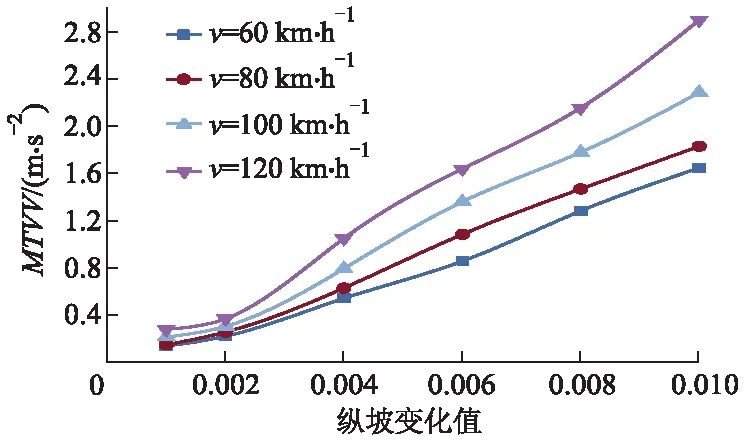
图5 L=8 m时MTVV变化规律

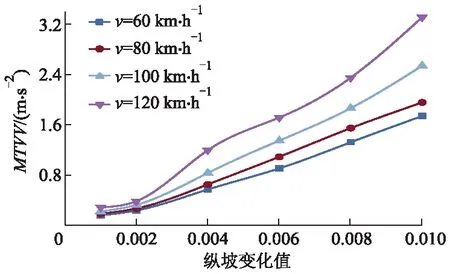
图6 L=10 m时MTVV变化规律

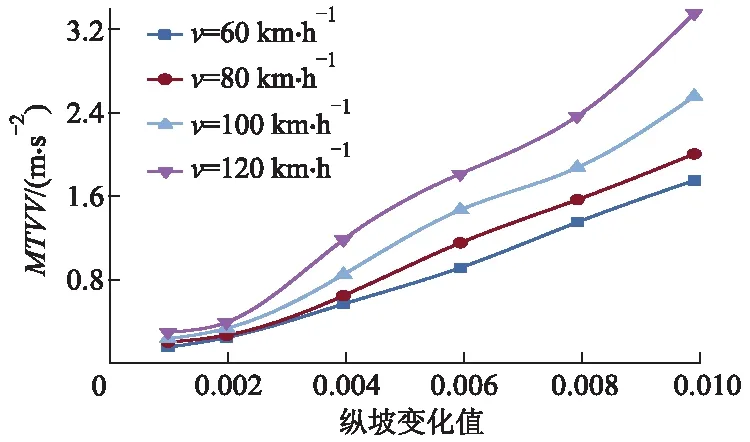
图7 L=12 m时MTVV变化规律

1) 搭板纵坡变化值的影响.仿真车辆以不同车速驶过不同长度搭板的路桥过渡段时,由搭板纵坡变化值引起的MTVV变化规律基本一致;当搭板纵坡变化值小于0.4%时,以同一车速通过不同搭板长度引起的MTVV值相差较小,当纵坡变化值高于0.4%时,MTVV值相差逐渐变大.

2) 车速v的影响.对于同一搭板长度的路桥过渡段,当v<80 km·h-1时,MTVV随搭板纵坡变化值的增长幅度缓慢;当v>80 km·h-1时,MTVV增长幅度提高.可见,MTVV值对大于80 km·h-1的车速更为敏感.

3) 搭板长度L的影响.图8为搭板纵坡变化值为0.4%时不同搭板长度下MTVV变化曲线.显然,随着L的增加,不同车速下的MTVV值都会增长,最大增长幅度约为12%;同一速度下,车辆驶过L=10,12 m的桥头引起的MTVV值较为接近.

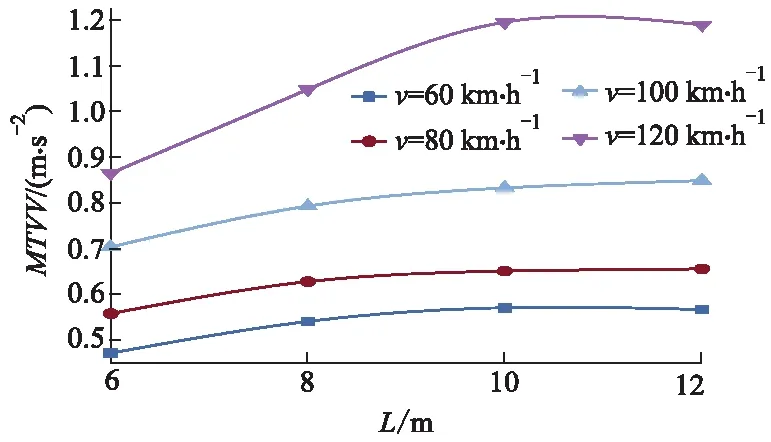
图8 纵坡变化值为0.4%时MTVV变化规律

2.2 不设搭板的路桥过渡段

车辆通过设有台阶的路桥过渡段时,先确定车辆前轮接触台阶时的时间点,然后取该时间点向后0.2 s之内的加速度数据进行处理.台阶高度与车速对最大瞬态振动值MTVV的影响如图9所示.

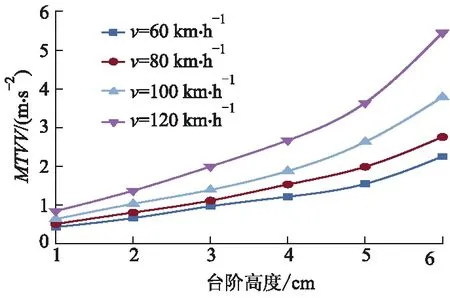
图9 不同台阶高度下MTVV变化规律

1) 车速的影响.相同台阶高度下,当车速由60 km·h-1增大到120 km·h-1,台阶高度为1～6 cm的MTVV分别增加了0.91～1.41倍;以v=80 km·h-1作为分界点,当v<80 km·h-1时,MTVV随台阶高度升高的增长率相对较小,当v>80 km·h-1时则增长率变大.

2) 台阶高度的影响.同一行车速度下,当台阶高度小于3 cm时,MTVV随着台阶高度的增高增长缓慢;当台阶高度高于3 cm后,每增加1 cm,则MTVV增加 33.6%～49.5%.可见,台阶高于3 cm时,对舒适性影响更强烈.

3 最大瞬态振动值分级标准

以京港澳、郑焦晋高速公路各路桥过渡段为试验地,对乘客通过不同桥头的行驶舒适性进行问卷调查,为降低因个体主观差异对舒适性调查的影响,随机抽取不同年龄、职业的健康公众人员参与小汽车以不同车速(60,80,100和120 km·h-1)驶过桥头时的人体舒适性进行问卷调查.调查中将乘客舒适性分为A,B,C和D等4个等级,每个等级对应的分值如下:A表示舒适(行车平稳无振动)为1分;B表示稍不舒适(有轻微振动)为3分;C表示不舒适(有振动)为5分;D表示很不舒适(有大幅振动)为7分.根据调查问卷,统计不同车速下每个等级的人数,并依据各舒适性等级所对应的分数,计算评分加权值μ.然后,根据每个桥头的实际状况结合模拟仿真结果,建立不同车速下人体舒适性评分与最大瞬态振动值MTVV的相关性对应数据.限于篇幅,仅提供车速分别为80,100 km·h-1的纵坡变化值、人体舒适性评分加权值与MTVV的对比表(见表2,3).

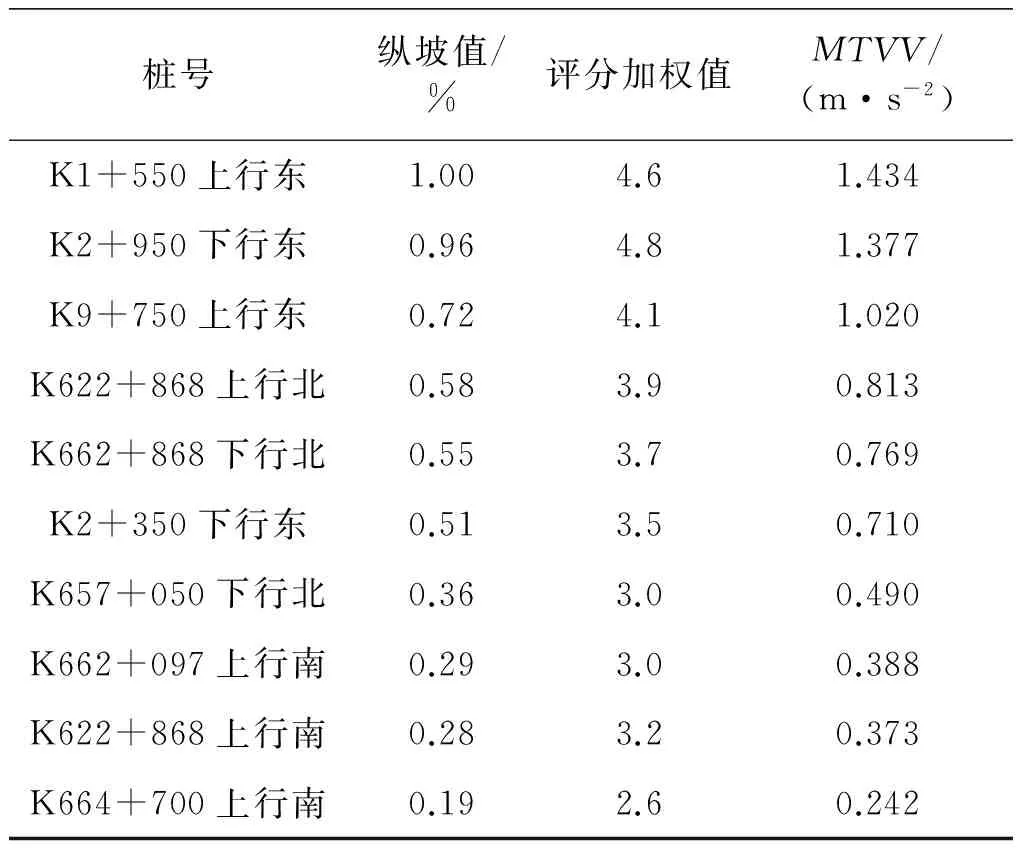
表2 车速为80 km·h-1时数据对比表

根据不同车速、不同桥头的人体舒适性评分加权值和MTVV数值,对二者的关系进行数值拟合,如图10所示.

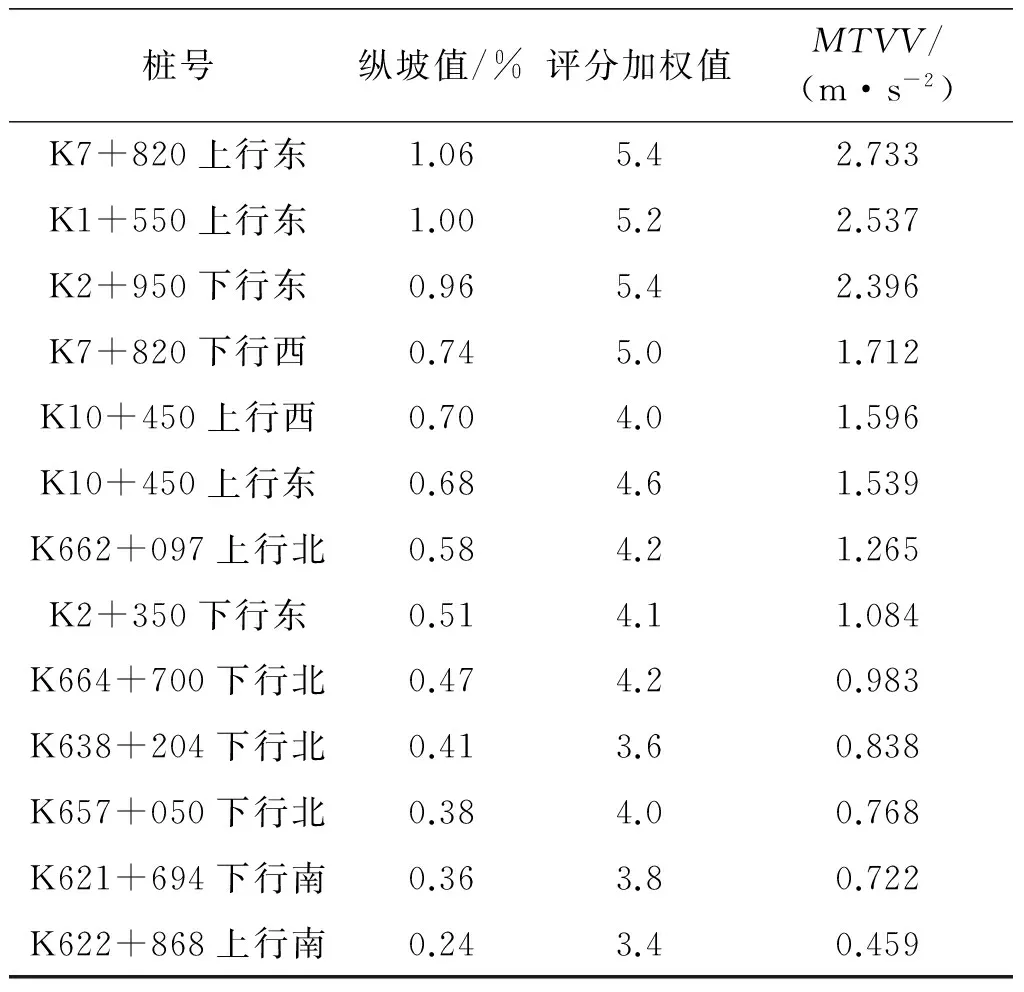
表3 车速为100 km·h-1时对比表

图10 舒适性评分加权值与MTVV值关系

结合图10中的人体舒适性评分值与MTVV的相关关系式、不同舒适程度对应的加权分值及ISO 2631-1:1997中对舒适性的划分,制定了最大瞬态振动值与人体舒适性感受对应表(见表4).

表4 最大瞬态振动值与人体舒适性感受对应表

4 容许差异沉降

以人体出现不舒适感受的MTVV低限,作为路桥过渡段容许差异沉降量化值的界限值,结合路桥过渡段各工况仿真结果拟合式,反算路桥过渡段的容许纵坡变化值、不设搭板的路桥过渡段容许台阶高度,计算结果见表5,6.

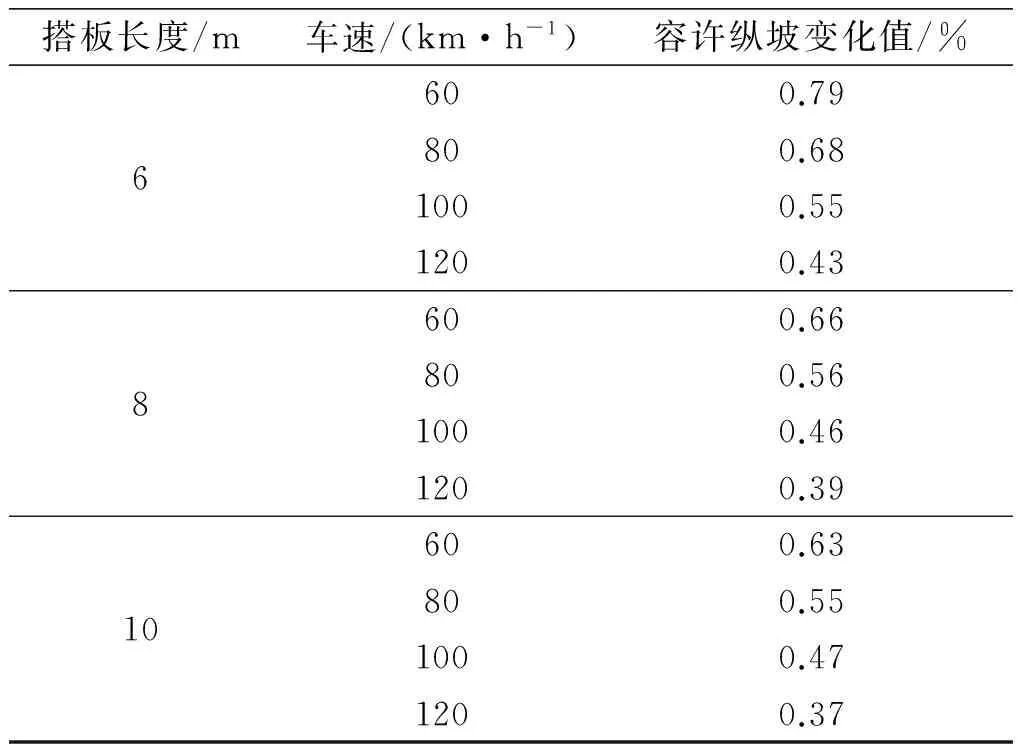
表5 容许纵坡变化值

表6 容许台阶高度

5 平整度评价方法

1) 简单评估法.简单评估法的评价指标为本研究提出的容许差异沉降值(见表5,6),评价路桥过渡段平整度时,量取路桥过渡段差异沉降值,并与表5,6中的数值进行比较即可,以舒适性程度来评判桥头路面平整度是否需要维修.

2)仿真评价法.仿真评价方法以最大瞬态振动值为平整度评价指标.步骤如下:以桑塔纳3000为模拟试验车,利用Carsim软件建立整车模型;实测路桥过渡段纵断面高程,根据实测数据进行路面建模;以设计车速进行人-车-路相互作用模拟仿真;仿真结束,输出座椅加速度数据,计算MTVV;结合表4对测试的路桥过渡段平整度进行评价.

6 结 论

1) 车速、纵坡变化值和台阶高度为MTVV的主要影响因素,3个影响因素均存在分界点,车速、纵坡变化值和台阶高度分界点分别为80 km·h-1,0.4%和3 cm.当低于分界点时,MTVV随各因素的增大而缓慢增长;当高于分界点时,则增长迅速.

2) 提出MTVV分级标准,分别针对设有搭板和不设搭板的路桥过渡段提出容许纵坡变化值、容许台阶高度.

3) 本研究以座椅作为振动舒适性评价点,进行桥头平整度的舒适性评价,提出了简单评估法和仿真评价法两种路桥过渡段平整度评价方法.

参考文献(References)

[ 1 ] 柏鲁甬, 雷电, 孙董, 等. DGR 技术在桥头跳车处治中的应用研究[J]. 公路交通科技 (应用技术版), 2017(5):266-268.

BO L Y, LEI D, SUN D, et al. Research on the application of DGR technology in treatment of bump on bridge approach area[J]. Journal of Highway and Transportation Research and Development (Application Edition), 2017(5):266-268.(in Chinese)

[ 2 ] 沈忱.桥头跳车病害分析及防治方法优化研究[D]. 武汉:华中科技大学, 2014.

[ 3 ] ROY S, THIAGARAJAN G. Nonlinear finite-element analysis of reinforced concrete bridge approach slab[J]. Bridge Engineering, 2007,12(6): 801-808.

[ 4 ] STARK T D, OLSON S M, LONG J H. Differential movement at the embankment/structure interface-mitigation and rehabilitation[C]∥Transport, Safety & Security. Illinois DOT, USA: The National Academies of Sciences, Engineering, and Medicine, Paper Number: 1995-297.

[ 5 ] 潘晓东, 杜志刚, 杨晓光. 桥头跳车对行车安全影响评价指标的研究[J]. 同济大学学报 (自然科学版), 2006, 34(5): 634-637.

PAN X D, DU Z G, YANG X G. Evaluation indexes of the impact of vehicle bumping at bridge-head on driving safety[J]. Journal of Tongji University(Natural Science Edition), 2006, 34(5): 634-637. (in Chinese)

[ 6 ] 何启魁, 田贵川. 沈大高速公路的桥头跳车及防治[J]. 东北公路, 1994(2): 47-48.

HE Q K, TIAN G C. Bump on Shen-da expressway and prevention[J]. Northeastern Highway, 1994(2): 47-48. (in Chinese)

[ 7 ] 冯忠居, 方贻立,龚坚城,等. 高等级公路桥头跳车的危害及其机理的分析[J]. 西安公路交通大学学报, 1999, 19(4): 33-35.

FENG Z J, FANG Y L,GONG J C,et al. Analysis of the harmful effect of vehicle bump at bridge-head of the highway and its mechanism[J]. Journal of Xi′an Highway University, 1999, 19(4): 33-35. (in Chinese)

[ 8 ] 沈宇鹏, 张尧禹, 柴树山, 等. 公路路桥过渡段搭板设计参数优化[J]. 北京交通大学学报, 2017, 41(3): 55-60.

SHEN Y P, ZHANG R Y, CHAI S S, et al. Optimization for design parameters of highway bridge approach slab[J]. Journal of Beijing Jiaotong University, 2017, 41(3): 55-60. (in Chinese)

[ 9 ] 郑木莲,孟建党,张世铎,等.路桥过渡段上车内人体舒适性评价方法[J].长安大学学报(自然科学版), 2012, 32(2): 1-6.

ZHENG M L, MENG J D, ZHANG S D, et al. Evaluation of method of human comfort in vehicle at transition section between bridge abutment and embankment[J]. Journal of Chang′an University(Natural Science Edition), 2012, 32(2): 1-6. (in Chinese)

[10] 韩浩. 公路路桥过渡段刚性楔形搭板应用研究及参数优化[D]. 北京:北京交通大学, 2017.

[11] WONG H K W, SMALL J C. Effect of orientation of approach slabs on pavement deformation[J]. Journal of Transportation Engineering, 1994, 120(4): 590-602.

[12] CAI C S, SHI X, VOYIADJIS G Z, et al. Structural performance of bridge approach slabs under given embankment settlement[J]. Journal of Bridge Enginee-ring, 2005, 10(4):482-489.

[13] 陶向华. 路桥过渡段差异沉降控制标准与人车路相互作用[D]. 南京: 东南大学, 2006.

[14] ZHANG H L. Determination of allowable differential settlement between bridge abutment and approach embankment with five-degree-of-freedom vehicle model[J]. International Journal of Pavement Research and Technology, 2010, 3(6): 311-319.

[15] CAPURUÇO R, HEGAZY T, TIGHE S, et al. Full-car roughness index as summary roughness statistic[J]. Journal of the Transportation Research Board, 2005, 1905(1): 148-156.

[16] 苏曼曼, 张洪亮. 基于整车车辆模型的沥青路面平整度评价方法[J].江苏大学学报(自然科学版), 2017, 38(3):361-366.

SU M M, ZHANG H L. Evaluation method of asphalt pavement roughness based on full car model[J]. Journal of Jiangsu University (Natural Science Edition), 2017, 38(3):361-366. (in Chinese)