基于流体力学方法的液化后砂土流滑推桩效应

陆建飞, 朱晓冬, 周恩全, 左 熹, 王炳辉

(1. 江苏大学 土木工程与力学学院, 江苏 镇江 212013; 2. 金陵科技学院 建筑工程学院, 江苏 南京 211169; 3. 江苏科技大学 土木工程与建筑学院, 江苏 镇江 212005)

桩基础是一种具有稳定性高、刚度大等优点的基础形式,普遍应用于建筑、桥梁等工程中.但是,近年来的震害资料表明,越来越多的桩基在地震液化场地中遭到了严重破坏.20世纪60年代以来,美国阿拉斯加地震、智利地震等都造成了大范围的地基土液化,出现严重的桩基破坏现象.1964年日本新瀉地震后调查发现一栋楼的桩基础毁坏严重,桩顶端钢筋混凝土碎裂,桩端附近产生很多的裂缝,日本著名的Showa大桥由于桩基附近土体液化严重，发生侧向变形,导致大桥发生垮塌破坏[1].1976年河北唐山大地震造成场地砂土严重液化,土体发生侧向移动,致使大量桩基桥梁和建筑桩基受到破坏[2-3].2008年汶川大地震的大范围土体液化导致一系列桩基发生了严重的破坏,其中小鱼洞大桥由于地基土液化造成桩基础发生剪切破坏错位,大桥桥面断裂倒塌[4].基于上述地基土液化导致的桩基础破坏案例资料,研究桩与液化土相互作用机理十分有必要.

以往,学者们均认为液化场地上部结构的惯性力导致了桩基的破坏,而液化后土体与桩的相互作用是以系数折减的方式来考虑液化场地桩的侧向承载力.因此,各国学者都进行各种各样的室内试验，研究液化场地桩的p-y曲线.文献[5]为了研究桩周液化土的孔压反应对p-y曲线的影响,进行了室内大型振动台模型试验.文献[6]通过振动台试验研究发现,土体初始相对密度和土体的深度决定了折减系数的取值.自此,人们认为场地桩基础毁坏就是由于液化土体的侧向大变形造成的.文献[7]通过桥梁桩基的大型振动台试验进一步得出,液化土层的侧向大位移对桩土相互作用影响很大.文献[8]认为对桩的内力反应起主导作用的是液化前上部结构传来的惯性力,液化土体的侧向变形是引起桩基础破坏的主要原因.文献[9]进行了离心机试验研究,试验结果表明：具有坡角的液化场地桩基的侧向位移比水平液化场地更为明显,而且发现地震液化引起的砂土侧向变形加大了桩身所承受的荷载.

上述研究都是从固体力学的角度来探讨液化后土体侧向变形对桩基的影响,目前有一种新颖的研究思路，即认为液化后砂土具有流体特性.本研究拟将液化后砂土视为牛顿流体和剪切稀化非牛顿流体,基于流固耦合思想,模拟研究在自重作用下，液化后砂土的流滑推桩效应.

1 流体和固体控制方程

把液化后砂土简化成流体,而把桩基础作为线弹性固体,因此,液化后的砂土和桩分别满足流体和线弹性固体的控制方程.

1.1 流体控制方程

将液化后砂土视为不可压缩的牛顿和非牛顿流体.因此,液化后砂土满足如下方程[10]：

1) 质量守恒方程,即

(1)

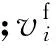
2)动量守恒方程(N-S方程).对黏性流体,其应力分量可表示为

(2)

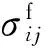
流体的动量守恒方程可表示为

(3)

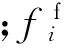
3) 本构方程.对牛顿流体[10],其黏性应力分量可表示为

(4)

(5)

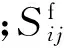
对幂律型非牛顿流体,其黏性应力分量[10-11]可表示为

(6)

式中:K为稠度系数;n为流动指数.当n<1时,流体为剪切稀化流体;当n>1时,流体为剪切变稠流体;当n=1时,表观黏度为常数,流体为牛顿流体.

1.2 固体控制方程

桩基础满足如下线弹性固体的基本方程[12]:

1) 几何方程,即

(7)

(8)

2) 应力-应变关系为

(9)

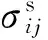
3) 运动方程，即

(10)

式中ρs为桩基础的密度.

1.3 耦合界面方程

流固耦合问题中,流体和固体除了应分别满足以上方程外,流固耦合界面还应满足相应的条件[13],从而将两者耦合起来求解.

运动学连续条件为

(11)

动力学连续条件为

(12)

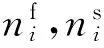
2 数值模型

将液化砂土看作不可压缩流体,空气为附加流体,基于流固耦合方法,并结合VOF方法对液化砂流滑推桩效应进行研究.VOF方法是利用单元中流体与单元体积比函数来描述自由液面的动态变化, 实际上是一种用于多相流体流动时捕捉流动界面的方法.因此,能够直观地看到液化砂土在流滑推桩过程中自由液面的变化过程.求解VOF模型过程中,首先定义体积比函数F,该函数满足以下VOF方程(以二维为例)[14]:

(13)

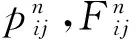
Ω=(xi-1/2,xi+1/2)(yj-1/2,yj+1/2)(tn,tn+1).

(14)

将方程(11)在控制体上积分得到

(Fn+1-Fn)δxδy+Δ(Fvx)δtδy+Δ(Fvy)δtδx=0.

(15)

定义如下:

Δ(Fvx)δt=min{FAD|Vx|+Ff,FDδxD},

(16)

式中:Ff=max{(1.0-FAD)|Vx|-(1.0-FD)δxD,0};|Vx|=|vxδt|.

A和D分别表示受主、施主单元.A或D的确定取决于网格内自由液面的方向及边界上的速度方向,FA,FD分别表示相应单元网格流体体积比函数.同理,可以构造Δ(Fvy)δt.

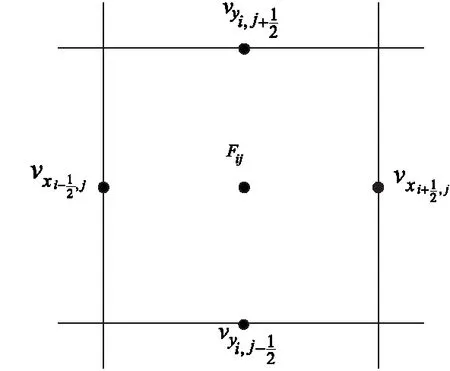
图1 非一致变量配置的Staggered格子

基于上述方法求解出体积比函数F,就可以构造出流体在相应单元网格上的自由液面,对控制方程进行离散.首先将质量守恒和动量守恒方程写成一个统一的微分表达式[16]:

(17)

式中:φ代表某一变量;Γ是扩散系数;S是源项.

将方程(17)进行高斯散度变换为

(18)

式中n为控制体积表面外法线方向向量.

将求解区域划分成有限个控制体积,利用有限体积法离散控制方程求解流体速度场.同时,将结构离散,建立结构的有限元网格模型,假设单元网格的位移模式,并导出单元的特性矩阵,综合每个单元的特性矩阵,得到结构系统的总体特性矩阵,最后得到结构的运动方程.通过求解N-S方程与结构运动方程的耦合方程,经过耦合界面的传递,从而求解流体与结构的耦合问题.

采用直接耦合方法,对液化砂土-单桩流固耦合系统进行计算.单桩模型和液化砂土模型分别在ADINA-Structures和ADINA-CFD模块建立.图2为流固耦合模型侧视图和俯视图.

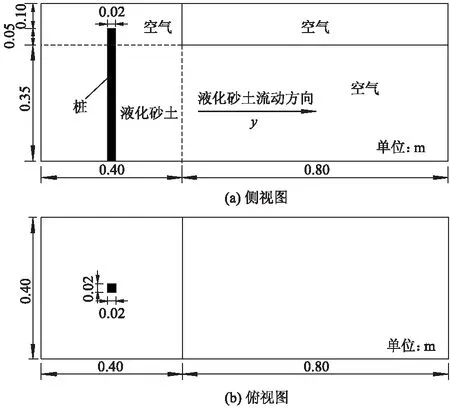
图2 计算模型示意图

3 计算与讨论

结构模型为底端固定、顶端自由的弹性方桩.采

用八节点单元,单桩顶端伸出液化砂土层0.05 m,其余部分为空气.流场底部、四周侧面为固壁,流场模型同样采用八节点单元.单桩埋在沙土中的部分和液化砂土接触面、单桩暴露在空气中的部分与空气接触面均为流固耦合界面.计算时间取6 s,单位时间步长0.005 s.具体结构模型参数如下： 液化砂土密度为1 600 kg·m-3，单桩的尺寸为长×宽×高=0.02 m×0.02 m×0.40 m，单桩的弹性模量为 3×1010Pa，单桩的泊松比为0.2，单桩的密度为2 500 kg·m-3.

3.1 考虑液化砂土为牛顿流体

将液化砂土视为牛顿流体,对液化砂土流滑推桩效应进行分析,认为在与桩的相互作用过程中液化砂土的流体性质保持不变,即黏度不变.本节计算分析了黏度分别为50,500,2 000 Pa·s时液化砂土流滑推桩效应.以黏度η=500 Pa·s为例,图3给出了液化砂土在t=0,0.5,1.0 s时的自由流动变形图,其结果与前期的研究相符合.

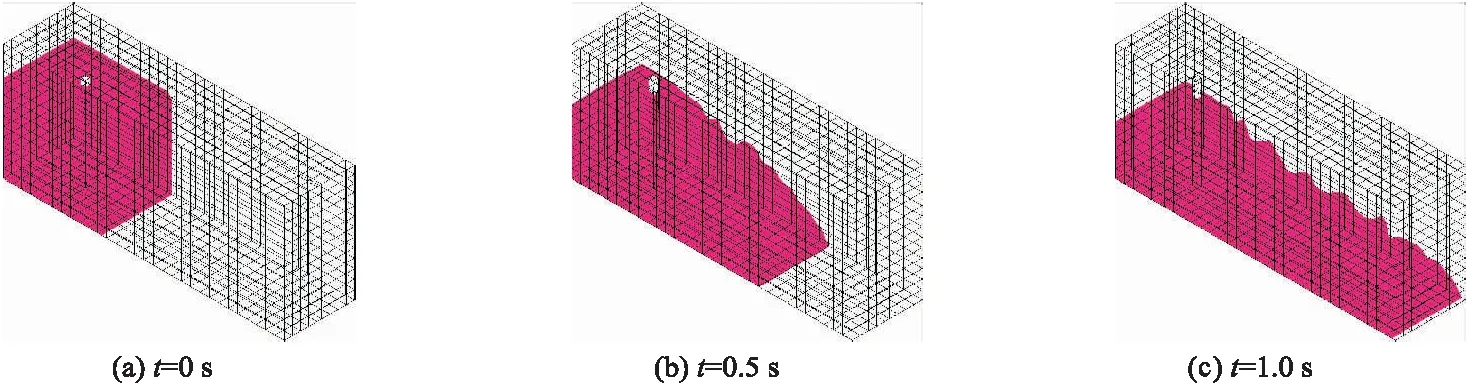
图3 液化砂土自由流动变形图

图4为桩身位移在距离桩底0.40,0.25,0.10 m这3个高度处的响应时程曲线和桩身应力在距离桩底0.40,0.20,0 m 这3个高度处的响应时程曲线,图中最终时间为模拟终止时间,即流体流动到模型最右端的时间.由图4可知:单桩位移在距离桩底越远处响应越大,距离桩底越近处变化越缓慢;应力响应则是距离桩底越近处响应越大,距离桩顶端越近处变化越缓慢.

图5为3种液化砂土黏度下液化砂土-单桩流固耦合系统的桩身y方向位移和桩身应力峰值响应曲线(即在模拟终止过程中的最大值).由图5可知:在给定黏度下,桩顶端位移响应最大,越靠近桩底,位移响应就越小,桩身应力在桩底最大,越靠近桩顶,桩身应力越小,与图4相呼应，即在同一桩身位置处,液化砂土的黏度越大,桩身位移和桩身应力峰值反应越大,这是因为液化砂土的黏度越大,其抵抗变形的能力越强,在流动过程中对桩的推力越大,导致流固耦合作用中桩的响应越大.从曲线的变化发展来看,随着液化砂土的黏度增大,曲线之间的差距有越来越小的趋势.

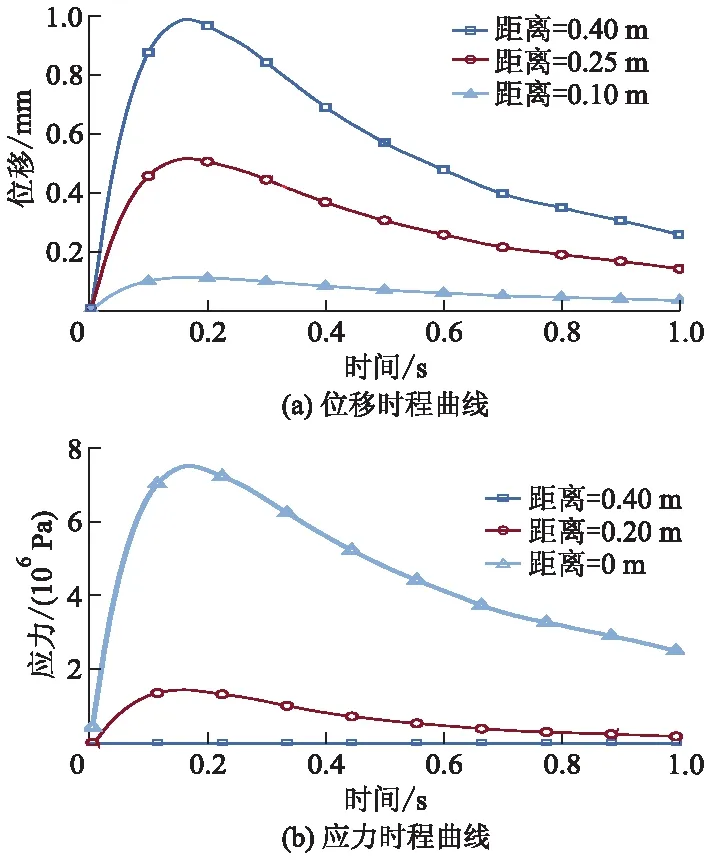
图4 单桩响应时程曲线

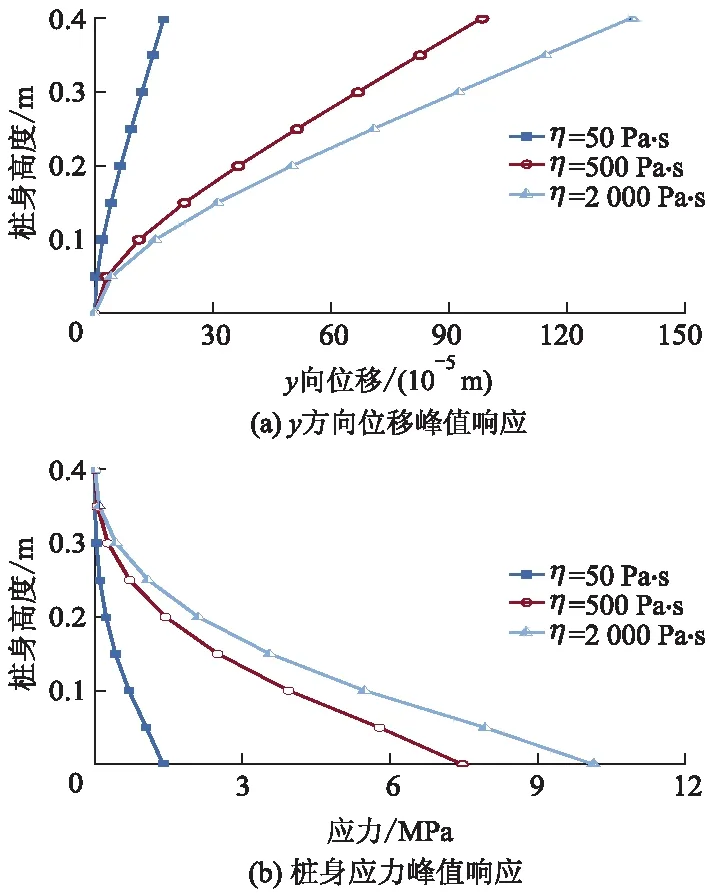
图5 不同黏度下桩身峰值响应

3.2 考虑液化砂土为非牛顿流体

本节将液化砂土视为幂律型剪切稀化流体,并考查了稠度系数K和流动指数n对流滑推桩效应的影响.非牛顿流体情况下的桩身位移和应力响应时程曲线规律与牛顿流体情况下的规律基本一致.非牛顿流体情况下流体参数见表1.

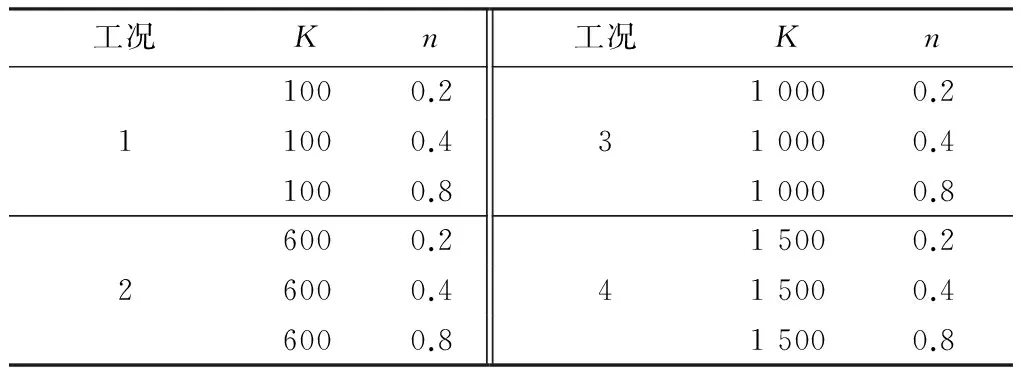
表1 流体参数

1) 稠度系数的影响.稠度系数K显著影响黏性流体的特征,K越大,表明流体的表观黏度越大,流体抵抗变形的能力也就越强.图6为流动指数n=0.8时不同稠度系数下液化砂土-单桩流固耦合作用下的桩身位移和应力峰值曲线.由图6可知,位移和应力峰值反应规律相当显著,桩身位移和应力发展规律与时程曲线规律保持一致.图6a中桩顶端位移响应最大,随着距离桩底越近,反应逐渐变小.在同一桩身高度处,稠度系数增大,位移跟着变大.从曲线之间的变化趋势可以得出,随着稠度系数的增大,曲线之间的差距越来越小.而图6b中桩身应力反应规律与图6a的情况相反,桩底应力最大,越靠近桩顶端应力越小.但是,同一桩身高度的应力也是随着稠度系数的增大而增大.曲线之间的差距同样随着稠度系数的增大而减小.由此可见,随着稠度系数的增大,稠度系数对位移和应力的影响逐渐变小.

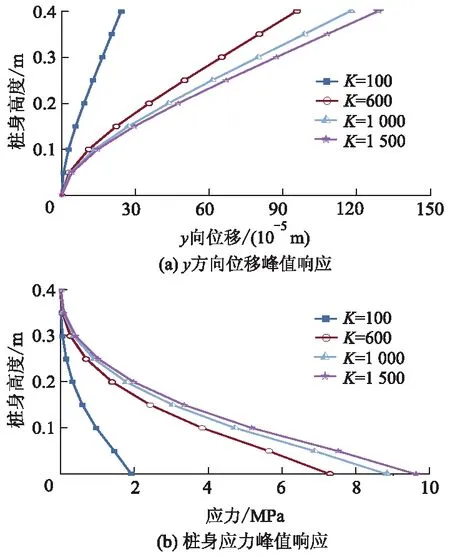
图6 不同稠度系数下桩身峰值响应

2) 流动指数的影响.对于剪切稀化非牛顿流体来说,流动指数n的范围为0～1.0.n越大表示该流体的非线性就越强,抵抗变形的能力也就越弱.图7为稠度系数K=600,液化砂土-单桩流固耦合作用时,不同流动指数下的桩身位移和桩身应力峰值的曲线.

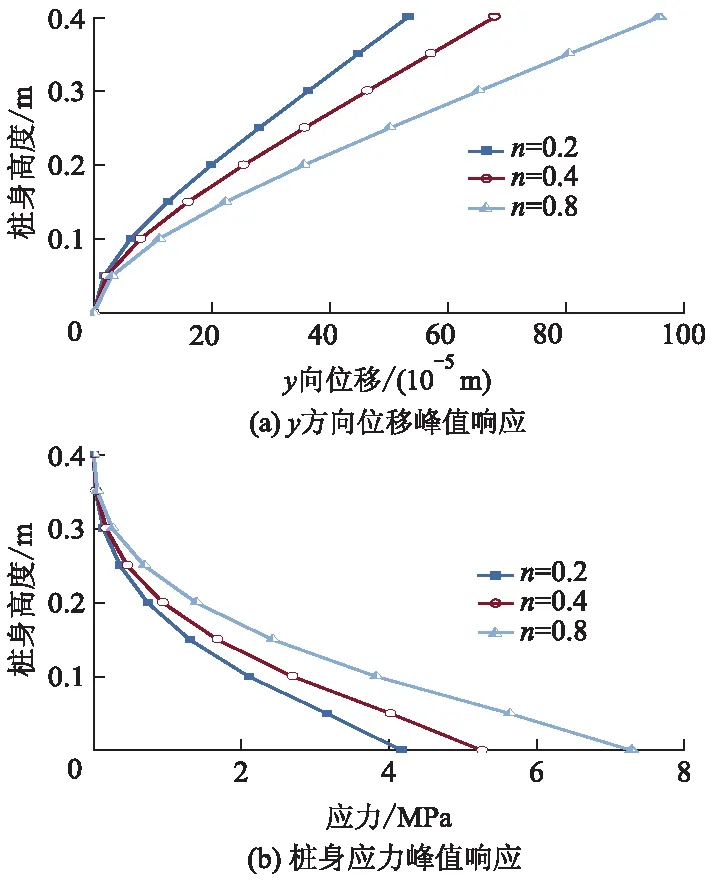
图7 不同流动指数下桩身峰值响应

图7a中,位移响应是桩顶端最大,越靠近桩底反应越小,同一桩身高度处,桩身位移随着稠度系数的增大而增大.图7b中,桩身应力响应规律与位移相反,桩底应力最大,越靠近桩顶端应力越小,沿桩身位移和应力大小与时程曲线规律保持一致.另外,桩身应力的变化规律和桩身位移基本一致,在同一桩身高度的应力随着流动指数增大而增大,这与稠度系数的影响情况下规律基本一致.

通过分析稠度系数和流动指数对桩身位移和应力的影响,可以知道二者的变化只对桩身位移和应力的大小产生变化,不会对变形方式产生影响.

4 结 论

1) 液化砂土流滑推桩效应沿桩身有显著规律性,桩顶处位移峰值响应最大,越靠近桩底响应越小,而桩身应力则在桩底最大,越靠近桩顶,应力越小,此规律适应于牛顿流体和非牛顿流体两种情况.

2) 将液化砂土视为牛顿流体,随着黏度增大,桩身的位移和应力就越大,且随着黏度增大,桩身响应曲线之间的差距有越来越小的趋势.

3) 将液化砂土视为剪切稀化非牛顿流体,液化砂土的流滑推桩效应同时受到稠度系数和流动指数的影响,且二者对桩身位移和应力的影响规律基本一致,即随着稠度系数和流动指数的增大,桩身位移和应力也不断增大.因此,稠度系数和流动指数的变化只会影响桩身位移和应力数值大小的变化,并不会对变形方式产生影响.

参考文献(References)

[ 1 ] HAMADA M. Large ground deformations and their effects on lifelines: 1964 Niigata earthquake[C]∥Case Studies of Liquefaction and Lifeline Performance During Past Earthquakes, Japanese Case Studies. New York, USA: National Centre for Earthquake Engineering Research, 1992.

[ 2 ] 刘恢先. 唐山大地震震害(一)[M]. 北京: 地震出版社, 1985.

[ 3 ] 刘恢先. 唐山大地震震害(三)[M]. 北京: 地震出版社, 1986.

[ 4 ] 吴珍汉, 张作辰. 汶川8级地震地质灾害的类型及实例[J]. 地质学报, 2008, 82(12): 1747-1757.

WU Z H, ZHANG Z C. Types and examples of geolo-gical hazards in Wenchuan Ms 8.0 earthquake[J]. ACTA Geologica Sinica, 2008, 82(12):1747-1757. (in Chinese)

[ 5 ] TOKIMATSU K, SUZUKI H. Power pressure response around pile and its effects onp-ybehavior during soil liquefaction [J]. Soils and Foundations, 2004, 44(6): 101-110.

[ 6 ] 王建华, 戚春香, 余正春, 等. 弱化饱和砂土中桩的p-y曲线与极限抗力研究[J]. 岩土工程学报, 2008, 30(3): 309-315.

WANG J H, QI C X, YU Z C, et al.p-ycurves and lateral resistances of piles in saturated degradation sand[J]. Chinese Journal of Geotechnical Engineering, 2008, 30(3):309-315. (in Chinese)

[ 7 ] 凌贤长, 唐亮. 液化侧扩流场地桥梁桩基抗震研究进展[J]. 地震工程与工程振动, 2015, 35(1): 1-10.

LING X C, TANG L. Recent advance in seismic analysis for bridge foundations in liquefaction-induced lateral spreading soils[J]. Earthquake Engineering and Engineering Dynamics, 2015, 35(1): 1-10. (in Chinese)

[ 8 ] TOKIMATSU K, ASAKA Y. Effects of liquefaction-induced ground displacements on pile performance in the 1995 Hyogeken-Nambu earthquake[J]. Soils and Foundations, 1998(2): 163-177.

[ 9 ] 汪明武, TOBITA T, IAI S. 倾斜液化场地桩基地震响应离心机试验研究[J]. 岩石力学与工程学报, 2009, 28(10): 2012-2017.

WANG M W, TOBITA T, IAI S. Dynamic centrifuge tests of seismic responses of pile foundations in inclined liquefiable soils[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(10): 2012-2017. (in Chinese)

[10] 王献孚,熊鳌魁.高等流体力学[M].武汉:华中科技大学出版社,2003.

[11] 陈育民,刘汉龙,周云东.液化及液化后砂土的流动特性分析[J].岩土工程学报,2006, 28(9):1139-1143.

CHEN Y M, LIU H L, ZHOU Y D. Analysis on flow characteristics of liquefied and post-liquefied sand [J]. Chinese Journal of Geotechnical Engineering, 2006, 28(9):1139-1143. (in Chinese)

[12] CHEN H F, SARIP A F. Elasticity and Plasticity[M]. Beijing: China Architecture and Buildng Press, 2005.

[13] 陈国兴,席仁强,王志华. 考虑流固耦合的桥墩地震反应方法[J]. 防灾减灾工程学报,2010,30(1):1-9.

CHEN G X, XI R Q, WANG Z H. Seismic response method of piers considering fluid-solid coupling[J]. Journal of Disaster Prevention and Mitigation Enginee-ring, 2010,30(1):1-9. (in Chinese)

[14] HIRT C W, HICHOLS B D. Volume of fluid (VOF) method for dynamics of free boundaries[J]. Journal of Computational Physics, 1981, 39: 201-225.

[15] 刘儒勋,舒其望. 计算流体力学的若干新方法[M]. 北京:科学出版社,2003.

[16] 张凯,王瑞金,王刚.Fluent技术基础与应用实例 [M].2版.北京:清华大学出版社,2010.