PLS通径模型的通信对抗装备系统效能评估分析

罗 乐，葛启东，杨 昱，祁世民

（中国洛阳电子装备试验中心，河南 洛阳 471003）

0 引言

武器系统效能评估是研制和使用该系统使用所追求的总目标，是武器系统发展论证和作战使用的总依据，对装备体系建设及其使用意义十分重要［1］。在复杂电磁环境下，电子信息装备系统效能的发挥受多种因素的影响，如何客观反映各因素之间的相互关系，准确分析各因素对效能的影响程度，发现制约效能提升的潜在因素，从而对其效能作出客观准确的评价是电子装备效能评估的热点问题。

由于装备体系日趋复杂，效能评估中涉及因素众多，各种因素之间相互关联，导致评估指标具有多重相关性［2］。并且由于电子信息装备试验任务条件和环境复杂性等原因，获取的数据样本数量较少、并不一定满足某种特定分布。这些特点都给电子信息装备系统效能评估带来一定难度。当前针对武器系统效能评估的方法主要有专家评定法、试验统计法、作战模拟法、指数法、解析法和多指标综合评估法［3］等。这些方法各有优缺点和适用范围。针对上述问题，本文尝试引入偏最小二乘通径模型（Partial Least-Squares Regression&Structural Equation Modeling，PLS-SEM），建立通信对抗装备系统效能评估框架，应用到通信对抗装备系统效能评估中。偏最小二乘通径模型［3］结合了偏最小二乘回归方法（Partial Least-Squares Regression，PLS）的算法优点和结构方程模型（Structural Equation Modeling，SEM）直接建模的优势，能够较好地描述复杂系统变量之间的结构关系，同时能够有效处理评估中相关数据多重共线性的问题，即使在样本较少的情况下也同样适用。该模型的应用可以为电子信息装备系统效能评估提供新的解决思路。

1 PLS-SEM模型原理

偏最小二乘通径模型［4-5］由Herman Wold等人于1983年提出，用以分析多组变量集合之间的统计关系。该模型的核心概念与结构方程模型一致，但采用偏最小二乘回归的求解思路，无需对观测变量作正态分布假设，对样本的个数要求比较宽松，能够有效处理变量的多重共线性问题，也为通信对抗装备系统效能评估提供了一种有力的工具。目前该模型在经济计量分析中得到了普遍的应用，但在军事领域研究较少。其中文献［3］对偏最小二乘通径模型在武器系统效能评估进行了适用性分析和应用性研究，对本文有一定的参考价值。

类似于结构模型［6］，偏最小二乘通径模型也由测量模型和结构模型组成。模型的计算则采用了偏最小二乘回归的算法。

1.1 测量模型

潜变量和观测变量是模型中的基本概念，其中潜变量无法直接测量，必须由观测变量推测得知。测量模型反映的是观测变量与潜变量之间的关系，目的是描述观测变量是否适合作为潜变量的测量手段。不同于结构方程模型，偏最小二乘通径模型中的测量模型中观测变量和潜变量的关系可以有2种方式表现，即反映方式和构成方式。

1.1.1 反映方式

反映方式是用潜变量表示观测变量的方式。设有J个潜变量，记为ξj（j=1，2，…，J），ξj对应的观测变量Xjl（l=1，2，…，pj）（j=1，2，…，J），反映方式可用一元线性方程表达，即

1.1.2 构成方式

构成方式是把潜变量表示成对应所有观测变量的线性组合，即

式中，ωjl为外部权重，εjl为残差项。

1.2 结构模型

结构模型用于描述潜变量之间的因果关系，可用一组线性方程组表达，即

式中，βjh为通径系数，ζj为残差项。

1.3 参数估计

由以上计算可知潜变量可以通过测量模型的构成方式来进行外部估计，也可以通过结构模型进行内部估计。偏最小二乘通径模型不考虑残差项，用观测变量来估计潜变量，有

式中，Wj为外部权重向量。

同时，潜变量还可以由相关的其他潜变量来估计，有

式中，αjh称为内部权数，按照如下方式计算：

Wj的估计可以表示为Yj对Xj作偏最小二乘回归的第一个轴向量，如下所示：

偏最小二乘通径模型对参数的计算采用迭代算法，分为以下4个步骤进行：

1）对数据进行标准化处理；

2）取向量ξˆj的初始值为 xj1，通过式（4）、式（5）计算Yj的值；

3）通过式（7）计算 Wj的值。

4）利用第 3）步计算的 Wj计算新的ξˆj，然后返回到第2）步，直到计算收敛为止。

利用最终得到的ξˆj和结构模型通过偏最小二乘回归得到通径系数，利用ξˆj和测量模型的构成方式通过偏最小二乘回归得到外部权重向量。

计算完成后要对模型的参数进行有效度检验，通过潜变量的组成信度（门槛值为0.7）、科隆巴奇系数（门槛值为0.7）和平均萃取变异量（门槛值为0.5）评价模型内在结构适配度。

2 模型建立和实例分析

2.1 模型构建

电子信息装备系统效能的发挥往往受到多种能力因素的影响，以某通信对抗装备系统为例，其效能的发挥通常体现在以下4个方面：1）对侦察和干扰分系统送来的信息进行综合分析处理，管理、组织、协调所属分系统的作战行动；2）实施通信对抗侦察，搜索、截获对方通信设备辐射的电磁信号，并对识别出的通信目标进行有效干扰，以达到削弱或破坏对方通信设备效能的目的；3）在需要战场转移时进行快速有效的机动；4）保障系统的通信畅通，维持装备良好的工作状态。结合上述分析，将以下4个能力指标作为系统效能评估的基本能力：指挥控制能力、通信对抗能力、机动能力和保障能力。各种能力通过可操作性的评估分指标来进行衡量［7］，如图1所示。

由图1可以看出各种能力的发挥是相互影响和制约的。例如指挥控制能力作为影响整个系统的重要因素，与其他各种能力互相关联；各种能力的评估指标之间也具有不同程度的关联性，存在多重相关性，例如：截获率、正确识别率和干扰有效率有较强的正相关性，展开、撤收时间能够影响到机动速度等等，以上这种多重相关性不满足传统树状指标体系对指标相对独立性的要求。同时，由于获取的有效数据较少，并不一定满足某种分布。上述原因给电子信息装备系统效能的评估带来一定的难度。

PLS-SEM模型能够有效处理存在多重共线性的数据，且在样本点数量要求上较为宽松，这2个方面的优点正好针对了系统效能评估相关数据处理时可能会出现的问题。另外，模型中对于观测变量和潜变量分别对应评估指标中的底层指标和能力指标是十分合适的。本例中模型将4种分能力指标视作潜变量，对应的评估分指标视作观测变量；作战能力视作综合潜变量，由其他4个潜变量来解释，同时作战能力的观测指标由所有的评估分指标组成。采用这种方法［8］能够较好地描述作战效能评估模型中各种变量以及相互之间的关系，如图2所示。

2.2 实例分析

由2.1节建立评估模型的测量模型和结构模型，模型的表达参照式（1）～ 式（3），模型参数 Wj，βjh的估计参照1.3节进行迭代和偏最小二乘回归计算。假设某次试验任务中，针对观测变量，共采集18组数据样本，并对数据进行标准化处理。将描述系统效能评估指标关系的模型和标准化处理后的数据输入到Smartpls软件中，经过迭代数据收敛到稳定解，如图2所示即为某通信对抗装备系统效能评估模型以及解算结果。图中椭圆形框为潜变量（ξ1，ξ2，ξ3，ξ4，ξ5）；矩形框内为观测变量（X1，X2，…，X12）。

对模型计算结果进行整理和归纳，绘制了相关图表。下页表1显示为各种潜变量和观测变量的因素负荷量；图4显示为4种能力对作战能力的贡献度比例。

2.3 评估结论

Smartpls软件提供了信效度衡量，实例模型中各潜变量对应的科隆巴奇系数均大于0.7，通过了偏最小二乘通径算法要求的唯一维度假设；潜变量的组成信度皆大于0.7，说明模型具有良好的内部一致性；平均萃取变异量皆大于0.5，表明测量模型具有较好的效度。

潜变量的路径系数分别为0.373、0.272、0.258、0.207，即对某通信对抗装备系统效能影响最大的为指挥控制能力，其次为通信对抗能力、保障能力和机动能力，4种能力的贡献度比例如图4所示。表1显示了各个观察变量与外生潜变量的的负荷系数，反映了变量之间的关系和相互作用的强弱程度，如在通信对抗能力方面，干扰有效率是影响的关键指标，以上结果与多数专家的定性判断基本一致。通过外部模型，由观测变量的外部权值还可计算各潜变量的值，从而对各种能力进行整体评价，更深层次的意义在于，这个方法能够给出武器系统效能定量的贡献度评价，找出影响武器系统效能发挥的关键因素和薄弱环节，为相关部门的装备研制和作战使用提供科学直接的依据。

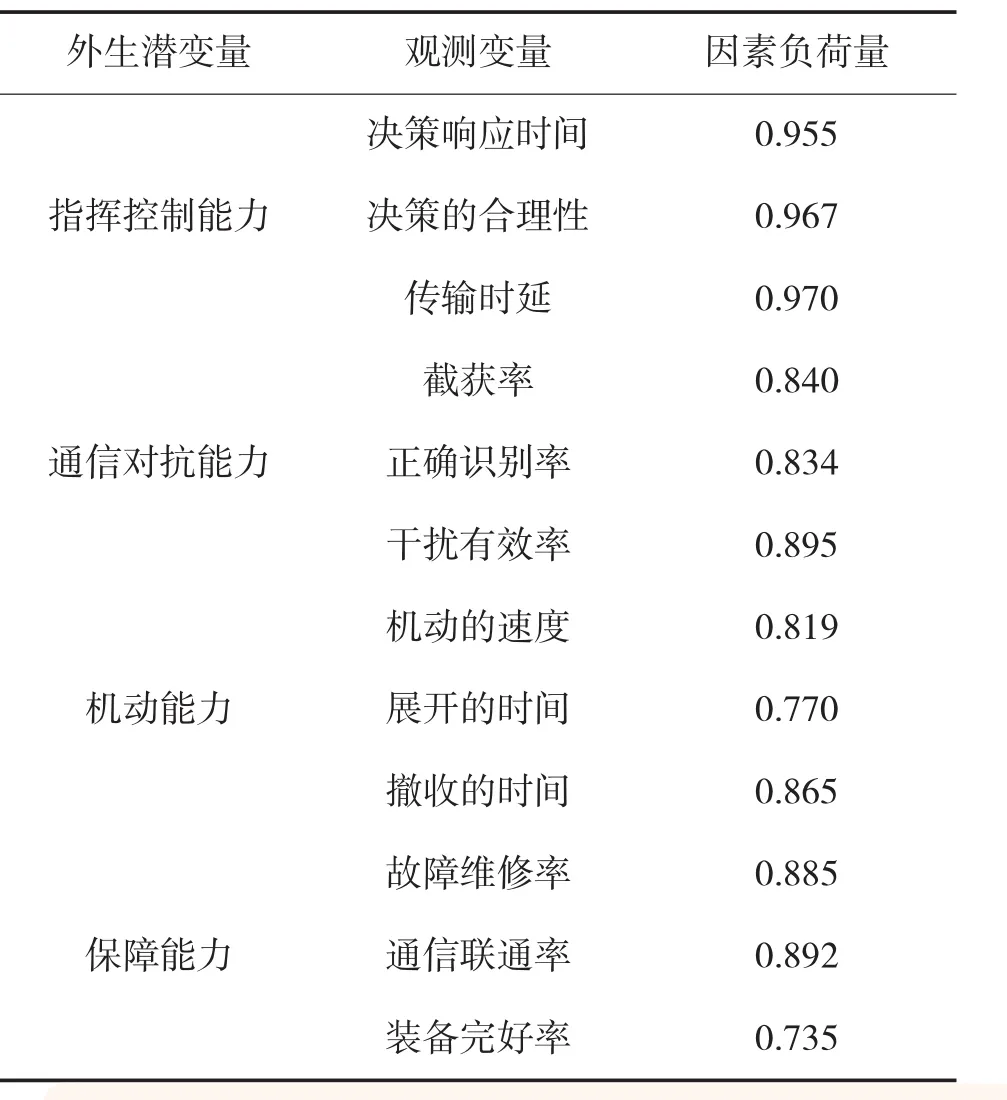
表1 外生潜变量与观测变量的负荷量

3 结论

本文研究了基于PLS通径模型的通信对抗装备系统效能评估分析方法，该方法能够有效地描述多种变量之间的相互关系，并克服评估指标多重相关性和数据样本少的问题，为电子信息装备系统效能评估中的多因素复杂影响问题提供了一种科学的定量分析方法。通过对某通信对抗装备系统效能的实例仿真和评估分析，其结果能够为装备研制和作战使用提供更为合理的依据，具有一定的现实意义。

需要指出的是，PLS通径模型具有较大的灵活性，在装备系统效能评估中，可以根据具体的问题来设置变量，采取更为复杂的路径关系建立多种因素的相互关系模型，并根据评估结果进行模型的修改和优化，解决武器系统效能评估中的实际问题。

参考文献：

［1］郭齐胜，郅志刚，杨瑞平，等.装备效能评估概论［M］.北京：国防工业出版社，2005.

［2］罗鹏程，周经伦，金光，等.武器装备体系作战效能与作战能力评估分析方法［M］.北京：国防工业出版社，2014.

［3］李志猛，徐培德.武器系统效能评估理论及应用［M］.北京：国防工业出版社，2013.

［4］WOLD S，ALBANO C.Pattern refression finding and using regularities in multirariate date［M］.London：London Analysis Applies Scinence Publication，1983.

［5］WOLD S.Modeling data tables by principal component and PLS：class pattern s and quantitative predictive telations［J］.Analysis，1984，12：477-485.

［6］王济川，王小倩.结构方程模型：方法与应用［M］.北京：高等教育出版社，2011.

［7］程岚.解析法在电子装备效能评估中的应用［J］.桂林电子工业学院学报，2003，23（6）：89-91.

［8］王庆丰.基于偏最小二乘回归通径模型的我国区域科技绩效综合评价［J］.统计与决策，2013，29（6）：111-113.