一种基于雷达资源管理优化的跟踪系统*

武 龙，许蕴山，龙文彪

（空军工程大学航空航天工程学院，西安 710038）

0 引言

一些国家为使雷达能够适应日益复杂的战场环境，在增强雷达探测性能方面做了大量研究，常用的方法有CV模型、Singer模型、EKF算法等。CV模型目标的运动形式单一，适应性不强，Singer模型是一种零均值时间相关模型，假设目标加速度的密度函数服从均匀分布，但该模型对具体运动的跟踪精度较低［1］。EKF算法通过对非线性方程进行一阶泰勒级数展开来估计目标运动状态，精度也不高，同时误差较大［2］。本文提出一种基于Kalman-SVMR算法及多传感器协同探测的雷达资源管理优化系统，通过对雷达量测缺失数据的补充替换提高了跟踪精度，改善了对目标的跟踪效果，有一定的针对性和研究意义。

1 Kalman滤波预测

假设某系统k时刻的状态方程及量测方程如下式：

其中，xk为状态变量，ωk-1为输入信号，vk为观测噪声，yk为观测数据。令，则可将非线性方程线性化处理后使用卡尔曼滤波。卡尔曼递推公式：

其中，Ak为状态方程增益矩阵，Ck为状态变量与输出信号之间的增益矩阵，Hk为加权矩阵，Rk为输入信号矩阵，Qk为观测噪声矩阵，xˆk为k时刻的状态估计值，其估计协方差矩阵的迹可反映出跟踪误差，即：

根据卡尔曼递推公式的推导过程，可以获得Kalman滤波的状态预测值及量测预测值分别为：

Kalman状态预测值的预测误差，可采用Kalman递推公式中的预测协方差矩阵的迹表示：

2 支持向量机回归

2.1 支持向量机回归算法原理

支持向量机是基于统计学发展起来的一种新的机器学习算法，其提高了模型算法的泛化能力，具有较好的推广能力及良好的分类性能［3］。支持向量机回归问题的标准形式，为一带约束的最优化问题。

其中，ξi表示松弛因子，C为常数（也叫惩罚因子）。采用LS-SVM算法，将条件限制中的不等式变为等式。其目标函数为：

该式可以通过Lagrange多项式求解，对应的Lagrange函数为：

其中，αk为Lagrange因子，根据KKT最优条件计算得到如下线性系统：

为利用Hestenes-Stiefel共轭迭代算法［4-5］，因此，得将上式中的系数矩阵转化为正定矩阵，由此上式可等效为如下方程：

对上式求解得最终解为：

最终的方程为：

2.2 单平台多传感器系统中的SVMR应用

假设给定传感器网络结构t时刻观测结点m的测量数据缺失，按照SVMR算法基本原理，将传感器网络中未缺失数据当作SVMR算法的输入项，缺失数据作为输出项，估计缺失数据［6］。具体过程如图1所示。

1）传感器获得目标的观测数据，经过预处理（如坐标转换、数据对准、模糊处理等），送入所对应的传感器网络观测结点。

2）假设t时刻观测结点m的数据丢失，将该结点t时刻以前的观测数据作为SVMR的输出，其他观测结点t时刻以前的数据作为输入，并将输入与输出集映射到高维空间H中，进行回归函数的训练［7-8］，获得回归函数。

3）在t时刻将未缺失数据的结点观测值当作训练得出的回归函数的输入对缺失数据估计。在此基础上获得完整数据集导入传感器网络的训练样本中，准备完成下一步参数学习工作。

3 跟踪系统建模与求解

3.1 系统建模

假设对某个目标设置的期望协方差矩阵为P0，控制矢量中，v（t）表示雷达 t时刻的工作方式［9］，v（t）=0 表示雷达不执行目标跟踪动作，v（t）=1表示雷达执行对目标跟踪动作，v（t）=2表示雷达受到干扰，无法对目标执行跟踪动作，v（t）=3表示采用支持向量机回归算法对目标距离进行预测［10］，则雷达资源管理的最优化模型为：，其

对于计量函数F［*］的选择形式，本文采用协方差差值最小准则，协方差的表达形式采用矩阵的迹表示，则雷达资源管理优化模型的具体形式为：

其中，tr（*）表示矩阵*的迹。

综合上述分析，给出传感器协同下的雷达跟踪框图如图2所示。

图2描述了多传感器协同卡尔曼-支持向量机无源跟踪算法流程。在tk时刻以前，传感器正常工作，能够有效测量目标运动参数，并将测量数据输入到支持向量机模型内，构造目标距离估计方程。tk时刻目标打开干扰设备，雷达无法正常发射脉冲测量目标距离向数据，扩展卡尔曼滤波判断预测值提供的目标跟踪精度是否满足跟踪精度，若满足则输出预测估计值对目标轨迹拟合［13-15］，不执行支持向量机步骤，否则以传感器测量角度数据通过支持向量机估计tk时刻的目标距离数据，将支持向量机估计距离值代替雷达观测值执行滤波，对目标航迹进行更新，同时将目标距离估计值送入支持向量机的训练样本中进行支持向量机的决策函数更新［16］。

3.2 模型求解

目标的离散化状态方程及量测方程为：

假设目标在某采样时刻tk的扩展卡尔曼滤波更新状态为：

其中，Pk为滤波协方差矩阵，P0为期望协方差矩阵，k为tk时刻的状态估计值，yk为观测值或者回归估计值。

由第2节可知，扩展卡尔曼滤波的滤波协方差矩阵及预测协方差矩阵为：

其中，Hk为扩展卡尔曼滤波增益矩阵，为量测方程的线性化因子。假定tk采样时刻的雷达控制矢量为：，若tk+1时刻的控制量为，则在tk+1时刻的目标跟踪误差协方差如下：

由式（15）可以计算出目标在tk+1时刻的误差协方差矩阵，将该跟踪误差协方差矩阵的迹代入式（12），就可以获得雷达资源的管理结果。

4 仿真验证

为说明该系统能够改善雷达对目标的跟踪效果，建立仿真模型进行验证。假设一个目标在三维立体空间中朝着我方雷达飞行，飞行轨迹为：

雷达的采样周期T为10 s，在x轴方向观测误差为11.40 m，在y轴方向观测误差为12.25 m。观测噪声及输入噪声为高斯白噪声，同时在目标飞行到（350，100，5.5）位置时，携带的干扰设备开机，雷达无法观测到目标，基于多传感器协同Kalman-SVMR无源跟踪算法对目标进行跟踪。目标的初始位置为（500，100，8），单位为 km。

本文根据留一法［17］（LOO，Leave_One_Out）对支持向量机的参数设定为：惩罚因子C=10 000，核参数σ=1。传感器协同中包含的传感器有ESM、IRST及雷达，其中各传感器的量测向量分别为：。量测噪声为，输入噪声为高斯白噪声。目标的初始位置为（500，100，8），采用二点起始法，确定协方差初值。传感器i与传感器j节点之间的转移概率为。

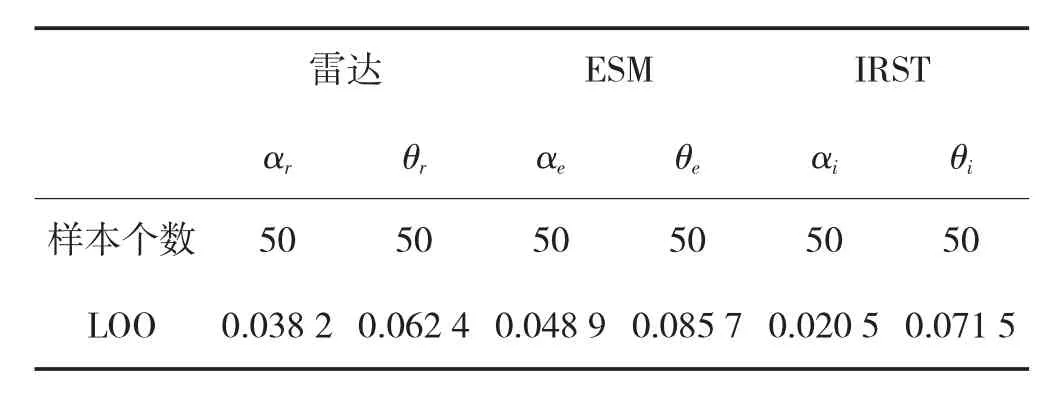
表1 LOO的错误率

由表1可知，LOO得到的错误率较小，说明SVMR回归函数具有良好的推广性。

从图3可知，在采样点50之后，敌方干扰设备对我机载雷达实施干扰，机载雷达将工作模式切换到无源工作模式，并在无源工作模式中调用本文设计的SVMR-Kalman无源滤波算法。从图4～图6明显看出传感器协同能够提高雷达对目标航迹的跟踪质量。雷达受到干扰后对目标的部分量测数据缺失，雷达采用卡尔曼滤波预测，当卡尔曼滤波预测值的跟踪精度低于期望跟踪精度值时，将支持向量机回归算法估计的雷达量测数据缺失值作为雷达的量测，继续进行卡尔曼滤波估计而不是卡尔曼滤波预测，相当于通过支持向量机回归算法将其他无源传感器的量测数据对雷达的缺失值进行了补充替换，实现了对目标的持续跟踪，精度较高。

5 结论

电磁干扰对雷达性能的发挥产生较大的压制，甚至对雷达造成毁灭性的破坏，导致目标航迹丢失。本文为改善雷达对目标的跟踪性能，将Kalman滤波跟踪算法和SVMR状态估计算法结合起来，设计了雷达无源工作模式中的跟踪滤波器算法，通过优化雷达资源管理及多传感器协同，解决了有源压制干扰条件下的目标航迹丢失问题。

参考文献：

［1］李海贵，孙俊平.通用雷达数据处理系统仿真测试平台设计［J］.雷达科学与技术，2010，8（4）：339-342.

［2］胡卫东，郁文贤，卢建斌.相控阵雷达资源管理的理论与方法［M］.北京：国防工业出版社，2010.

［3］VAPNIK V N.The nature of statistical learning theory［M］.New York：Springer Verlag，2000.

［4］龙文彪，夏海宝，刘庆林.多传感器目标指示交接动态联盟建模与分析［J］.传感器与微系统，2015，34（9）：30-34.

［5］刘向东，骆斌，陈兆乾.支持向量机最优模型选择的研究［J］.计算机研究与发展，2005，42（4）：576-581.

［6］王维佳，许蕴山，杨涛.无源传感器对雷达目标指示中触发准则研究［J］.传感器与微系统，2015，34（7）：21-25.

［7］WHITE K，WILLIAMS J，HOFFENSETZ P.Radar sensor management for detection and tracking［J］.Information Fusion，2008 11th international Conference on ，2008（7）：660-668.

［8］BLAIR W D，WATSON G A，HOFFMAN S A.Benchmark problem for beam pointing control of phased array radar against maneuvering targets［C］//Proc.Of 1994 American Control Conference，Baltimore，MD，1994，2071-2075.

［9］高娜.雷达抗干扰技术研究［D］.南京：南京理工大学，2008.

［10］宋晓峰，陈德钊，胡上序.支持向量机泛化能力估计若干方法［J］.计算机科学，2004，31（8）：125-126.

［11］赵一兵，王荣本.基于多传感器信息的前方障碍物检测［J］.计算机工程与应用，2007，43（26）：174-179.

［12］王立琦，侯彦鹏.一种新的异类传感器信息融合算法［J］.计算机工程与应用，2016，52（6）：107-110.

［13］吴文浩，李悦丽.基于WNNs的ADS与多雷达航迹融合算法［J］.计算机工程与应用，2011，47（27）：225-230.

［14］许婉君，侯志强.背景加权的多特征融合目标跟踪算法［J］. 空军工程大学学报（自然科学版），2015，16（2）：71-76.

［15］贵彦乔，吴彦鸿，俞道滨.跟踪雷达干扰技术综述［J］.兵器装备工程学报，2017（4）：141-147.

［16］郇宇，赵伟光，张红梅.基于距离加权的雷达内插去噪算法［J］.计算机工程与应用，2012，48（33）：157-160.

［17］王坤赤，郑月节，徐晨.一种改进的无线传感器网络最小跳数路由协议 ［J］.传感器与微系统，2012，31（8）：52-57.