线性规划问题的实际应用
王震
线性规划是现代数学中研究最优化理论的重要模型.它的实际运用范围十分广泛,从解决技术问题的最优化到工业、农业、商业、交通运输、经济、军事等众多领域都发挥作用.简单线性规划这部分内容体现了新教材重视数学应用,重视知识的发生发展过程,贴近生活的特点.为了让学生学好简单线性规划知识,提高学生运用线性规划知识解决实际问题的能力,本文对高中数学中线性规划问题的应用进行了剖析,对此类问题的求解思想和一般步骤作了较详细地阐述.
1整数最优解的确定
求最优解的问题,特别是当实际问题要求最优解是整数时,这是线性规划问题图解法中最重要而且是最难完成的一个环节,怎样来确定符合条件的整数最优解呢?主要方法有四:
(1)直接求解法,适用于多边形的角点坐标恰好是整数最优解;
(2)观察法,此法适用于由可行域直接可看出的;
(3)边界找点法;
(4)进一法或去尾法.后两种方法是不能直接求得又不能由图看出的情况下来运用的.
它既需要由图形的直观性又需要适当的计算,应用数形结合的数学思想.
例1某运输公司有7辆载重6t的A型卡车,4辆载重10t的B型卡车,有9名驾驶员.在建造某段高速公路中,公司承包了每天至少运输沥青360t的任务.已知每辆卡车每天往返次数为A型8次,B型6次,每天运输成本为A型160元,B型252元.每天应派出A型、B型车各多少辆,能使公司总成本最低.
解分析列表如下: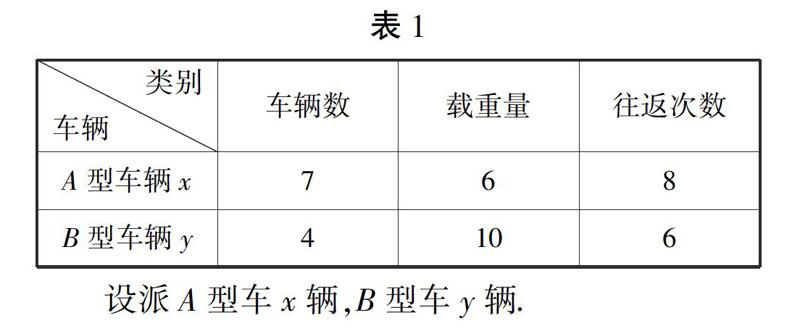
目标函数:z=160x+252y.
由图1可知,当l:160x+252y=0向右上方平移至l′的位置时,直线经过可行域上的点A,y轴截距b=1252z最小,即z最小.
由方程组4x+5y=30,
x=7.
解得點A(7,25).25不是整数.调整,整数解为最优点E(5,2).
当x=5,y=2时,总成本z=160×5+252×2=1304(元).此时运输沥青吨数为8×6×5+6×10×2=360(t).
即每天应派A型车5辆,B型车2辆,总成本1304元最低,并能运沥青360吨.
在上述解答中,虽然可行域给出目标函数z的最小值,但不符合实际问题的最优解是非负整数的条件,这时应该进行调解.“就近原则”.本题中与点A最近的整点是F(7,1),此时总成本z=160×7+252×1=1352(元),比 z=1304(元)高,所以调整的关键是寻求与可行域边界接近的整点(不妨简称边界找点法).也就是缩小可行域来寻找它的整数解,如果整点数不止一个,则逐个比较目标函数的取值,确定最优整点,得到最优解.
例2要将两种大小不同的钢板截成A、B、C三种规格,每张钢板可同时截得三种不规格的小钢板的块数如下表所示:
钢板类型A规格B规格C规格第一种钢板211第二种钢板123解今需要A、B、C三种规格的成品分别为15、18、27块,问各截这两种钢板多少张可得所需的三种规格的成品,且使所用钢板张数最少解:
设两种钢板分别要x,y张,则其线性约束条件为:
2x+y≥15,
x+2y≥18,
x+3y≥27,
x≥0,y≥0.作出可行域如图2所示,
图2其目标函数为z=x+y.
(那么,怎样寻找其最优整数点呢?分解小步骤如下:)(步骤1)作出一组平行直线x+y=t中经过可行域内的点且和原点距离最近的直线;
(步骤2)此直线经过直线x+3y=27和直线2x+y=15的交点A(185,395);
(步骤3) 过交点A(185,395)的目标函数线的方程为x+y=575;
(步骤4) 由于185,395都不是整数,所以可行域内的点A(185,395)不是最优解;
(步骤5) 找出与575=11.4(x+y=575)接近的,且适合题意的整数解(此法简称为进一法或去尾法).经过可行域内的整点且与原点距离最近的直线是x+y=12;
(步骤6) 所以适合题意的整点为B(3,9),C(4,8),即为所求最优解.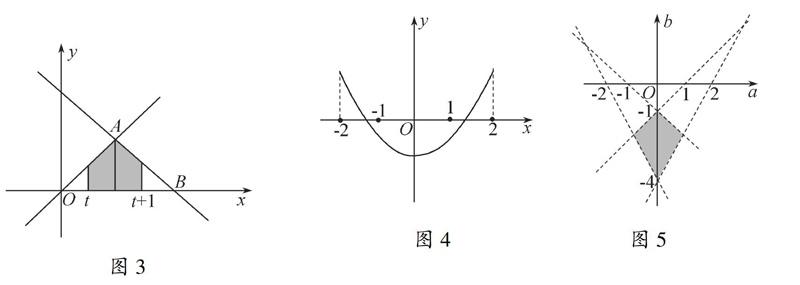
2阴影部分面积的确定
例3在直角坐标平面内,有两个区域M和N,M是由y≥0和y≤x,y≤2-x这三个不等式确定;N是随t而变化的区域,它由不等式t≤x≤t+1决定,t的取值范围0≤t≤1,求M和N的公共部分的面积S(t).
解设定区域M为不等式组y≥0,
y≤x,
y≤2-x,
所围成的区域,即△AOB所围成的区域(含边界)(图3).图3 动区域N是两条动直线x=t,x=t+1(0≤t≤1)所构成的带状域.
因此,M和N的公共部分为图3的阴影部分(含边界)的面积,此面积为两个梯形面积之并.
即S(t)=12(1+t)(1-t)+12[1+(1-t)]t =-t2+t+12(0≤t≤1).
3参数取值范围的确定
例4如图4所示,当方程x2+ax+b=0的一根在-2和-1之间,另一根在1和2之间时,用图形表示以a,b为坐标的点(a,b)的存在范围.
解如图4,设fx=x2+ax+b,依题意,得
f(-2)=4-2a+b>0,
f(-1)=1-a+b<0,
f(1)=1+a+b<0,
f(2)=4+2a+b>0.即b>2a-4,
b b<-a-1, b>-2a-4.图4图5在a,b坐标平面内作出该不等式组的平面区域如图5的阴影部分(不包括边界)为(a,b)的取值范围. 二元一次不等式组的平面区域,实际上就是二元一次不等式组的几何表示.解题时,依题意,作出约束条件的公共部分,就能直观地解决所求问题. 中学数学中的线性规划内容既给传统的教材注入了新鲜的“血液”,又给学生提供了学数学、用数学的实践机会,同时促进了与不等式、方程、函数等知识的整合.通过本知识的学习,学生将初步掌握线性规划的一些基本理论、一般方法,将为线性规划知识的后续学习打下基础,为线性规划知识的广泛应用拿到一枚入门的钥匙.

