采用最优化拟合法计算水驱气藏动储量及水体大小

廖恒杰 鹿克峰 杨志兴 李元生

(中海石油(中国)有限公司上海分公司研究院， 上海 200335)

水驱砂岩气藏水侵预测及动储量计算是气藏生产动态研究的基础性工作，对水驱气藏后期调整挖潜具有重要的指导意义。目前，国内外学者针对水驱气藏水侵预测与动储量计算方法作了大量研究[1-6]。常用的水侵量计算模型有Schilthuis稳态模型，VanEverdingen和Hurst非稳态模型，Fetkovich拟稳态模型[7-10]。但是这些模型的假设条件较多，计算过程繁琐复杂，且不易获取常用的水域静态、动态参数，计算结果偏差大，不利于实践操作，难以推广应用。张伦友等人提出了水驱气藏水侵研究的经典关系式lnω=BlnR[11]，通过水侵体积系数与采出程度关系曲线拟合得到水侵常数B，并据此判断水侵强度。该方法必须依赖地质储量，只有正确计算水驱气藏的动储量，才能客观评价水驱气藏水侵强度。基于此理论，本次研究中尝试将水驱气藏物质平衡与Fetkovich拟稳态水域模型相结合，采用试算法调整水侵常数B，以实现水驱气藏动储量与水体大小的同步预测。

1 基本原理及方法

根据地下体积平衡的原理，在相同的压力、温度条件下，开采过程中地层压力下降所产生的地下天然气体积膨胀量、束缚水膨胀量、气藏孔隙体积减少量及天然水侵量之和与油气水地下累计采出量相等，则水驱气藏物质平衡方程式可表示为：

(1)

式中：G—— 储层原始天然气储量，108m3；

Bg—— 当前地层压力下天然气的体积系数；

Bgi—— 原始地层压力下天然气的体积系数；

Cw—— 水的压缩系数，MPa-1；

Cp—— 岩石的压缩系数，MPa-1；

Swi—— 束缚水饱和度；

Δp—— 气藏地层压力降，MPa；

We—— 天然累计水侵量，m3；

Gp—— 累计产气量，m3；

Wp—— 累计产水量，m3；

Bw—— 当前地层压力下地层水的体积系数。

当忽略气藏压力下降后导致的岩石孔隙体积减少及束缚水膨胀时，水驱气藏物质平衡方程可表示为[12-14]：

G(Bg-Bgi)=GpBg+WpBW-We

(2)

令：

F=GpBg+WpBw

(3)

Eg=Bg-Bgi

(4)

则式(2)可变换为：

(5)

式中:F—— 油、气、水的地下累计采出量，m3；

Eg—— 天然气弹性膨胀系数。

在生产动态资料详实的情况下，产量数据、压力史及PVT性质均为已知，可以据此计算出每个地层压力下的天然气、地层水的体积系数，进而求解Eg及F。方程中的未知数G与We无法直接通过物质平衡方程求解，因此可将水驱气藏物质平衡与Fetkovich拟稳态水域模型相结合，用于计算水侵量，从而解决动储量计算问题。

Fetkovich拟稳态模型水侵量与水域总压降的计算公式可表示为：

(6)

式中：pi—— 原始地层压力，MPa；

Va—— 水域体积，104m3；

Ce—— 水域压缩系数，MPa-1；

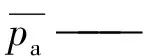
Fetkovich拟稳态模型将预测时间划分为等时步长，则计算总压降的实用关系式表示为：

(7)

(8)

(9)

(10)

(11)

pf,1—— 1时间步末气水界面处压力，MPa；

B—— 水侵常数。

将物质平衡方程与Fetkovich水域模型相结合，可得到新的方程式：

(12)

令：

(13)

(14)

则式(12)可变换为：

Y=G+VaCeX

(15)

式中存在动储量、水侵常数、单位压降水侵量这3个未知数，无法直接求解。需要通过调整水侵常数B，使Y—X的线性相关系数最高，其截距即为动储量，斜率即为单位压降水侵量VaCe。另外，只要获知水域综合压缩系数Ce，即可得到水体体积，进而计算出水体倍数，并据此判断水体能量的大小[15-19]。

2 实例分析

以东海某典型水驱气藏为例进行分析，该气藏于2011年投入生产，其基本参数如下：静态地质储量为27×108m3；原始地层压力为27.96 MPa；原始地层温度为124.3 ℃；储层孔隙度为16%；渗透率为35×10-3μm2。对开发井进行了地层流体PVT取样及实验室PVT分析，获得水域有效压缩系数Ce(0.001 015 MPa-1)。天然气偏差因子Z与压力p的关系为：

Z=-0.000 002 1p3+0.000 359 0p2-

0.008 359 5p+0.993 378 5

实测地层压力表现出先下降后回升的趋势，开发稳产阶段为线性下降特征，开发中后期压力数据有明显的上升，显示出中强水驱的气藏特征。表1所示为气藏生产动态数据。

表1 气藏生产动态数据

根据生产数据计算出地下流体总采出量F及气藏不同压力下的体积系数Bg，进而求取天然气弹性膨胀系数Eg，代入式(13)，即可计算出各时间步的Y值。表2所示为气藏生产动态数据及计算得到的参数值。

根据式(14)计算出不同的水侵常数B，再分别计算不同时间步长的水域总压降，进而计算出不同时间步长的X值，绘制出不同水侵常数的Y与X回归曲线，然后将每组数据回归得到的相关系数进行拟合分析，可以得到二次方的R2与B的关系式。不断重复这一过程，直到相关系数达到最大值为止，相关系数最大值对应所需求取的水侵常数B。绘制的回归曲线G值即为水侵校正后的动储量，斜率为单位压降的水侵量。表3、表4、表5为水侵常数B取不同值时的Fetkovich解析水域模型法计算数据。图1所示为不同水侵常数下的生产数据拟合曲线。

表2 气藏生产动态数据及计算得到的参数值

表3 Fetkovich解析水域模型法计算数据(B取0.10)

表4 Fetkovich解析水域模型法计算数据(B取0.27)

表5 Fetkovich解析水域模型法计算数据(B取0.40)

图1 不同水侵常数B值下的生产数据拟合曲线

根据水侵常数B与方程相关系数关系曲线(见图2)可知，相关系数与水侵常数呈二次方抛物线关系。回归数据求导分析结果显示，水侵常数为0.27 时，相关系数最好。因此，认为该气藏水侵常数B为0.27，对应截距即动储量值为31.05×108m3，斜率即单位压降水侵量为70.76×104m3MPa，计算地下水体积为69 716×104m3，水体倍数为46倍。显然该气藏的水体能量较强，建议控制好采速，防止生产井过早水淹。

图2 水侵常数B值与方程相关系数关系曲线

3 结 语

本次研究将物质平衡原理与解析水域模型相结合，采用最优化拟合法，进行水侵量、动储量计算，分析水体大小。该方法计算过程简单，容易实现，具有较强的矿场使用价值。采用最优化拟合法计算出的气藏动储量为31.05×108m3，大于静态法评估的地质储量。这主要是由于气藏内部发育多个边水气藏，生产井未钻遇气水界面，说明该气藏的储量存在升级的空间。计算结果表明，该气藏的水体倍数为46倍，显示水体能量较强，建议密切跟踪生产动态，适当控制生产制度，防止生产井过早水淹。

[1] 刘世常，李闽，巫扬，等.计算水驱气藏地质储量和水侵量的简便方法[J].新疆石油地质，2008，29(1)：88-90.

[2] 胡俊坤，李晓平，张健涛，等.计算水驱气藏动态储量和水侵量的简易新方法[J].天然气地球科学，2012，23(6)：1175-1178.

[3] 唐川，赵家辉，张俊松，等.考虑水封气的水驱气藏动态储量计算新方法[J].天然气与石油，2013，31(1)：63-66.

[4] 王怒涛，黄炳光，张崇军，等.水驱气藏动态储量及水侵量计算新方法[J].西南石油学院学报，2000，22(4)：26-28.

[5] 袁淋，李晓平，苏广乐.水驱气藏动态储量及水侵量确定新方法[J].石油天然气学报(江汉石油学院学报)，2014，36(11)：178-181.

[6] 胡俊坤，李晓平，宋代诗雨.水驱气藏动态储量计算新方法[J].天然气地球科学，2013，24(3)：628-632.

[7] 邹宇,戴磊，李士伦，等.水驱气藏水侵量的计算方法[J].西南石油学院学报，1997，19(1)：102-108.

[8] 李传亮.气藏水侵量的计算方法研究[J].新疆石油地质，2000，24(5)：430-431.

[9] 吴克柳，李相方，许寒冰，等.考虑反凝析的凝析气藏水侵量计算新方法[J].特种油气藏，2013，20(5)：86-88.

[10] 吴克柳，李相方，范杰，等.异常高压凝析气藏水侵量及水体大小计算方法[J].中国矿业大学学报，2013，42(1)：105-111.

[11] 张伦友，孙家征.变容物质平衡方法及其在气田开发中的应用[J].天然气工业，1991，11(5)：58-64.

[12] 冯景林.基于Havlena_Odeh法求取水驱气藏单井控制动态储量的简便算法[J].中国海上油气，2006，18(2)：255-257.

[13] 刘建仪，韩杰鹏，张广东，等.单井生产动态拟合法求取强水驱凝析气藏动态储量[J].中国海上油气，2016，28(2)：83-87.

[14] 唐毅，杨国，罗阳俊，等.计算产水气藏地质储量和水侵量的简便方法[J].钻采工艺，2010，33(5)：69-71.

[15] 杨琨，王怒涛，张建民.水驱气藏水侵量及水体参数计算方法研究[J].大庆石油地质与开发，2005，24(5)：48-50.

[16] 王怒涛，张建民，章彤，等.遗传算法在水驱气藏地质储量及水侵量计算的应用[J].石油工业计算机应用，2004，12 (3)：13-16.

[17] 匡建超，史乃光，杨正文.综合总目标函数最优化方法计算水驱气藏储量与水侵量[J].天然气工业，1993，13(6)：41-46.

[18] 唐圣来，罗东红，闫正和，等.中国南海东部强边底水驱气藏储量计算新方法[J].天然气工业，2013，33(6)：44-47.

[19] 刘一江，康晓东，李相方，等.气藏水体规模的不确定性分析[J].新疆石油地质，2005，26(2)：183-185.