用于求解路径交通流量的改进Frank-Wolfe算法

柴 获，何瑞春，马昌喜，代存杰

CHAI Huo1，2,HE Ruichun2,MAChangxi2,DAI Cunjie1，3

1.兰州交通大学 机电技术研究所，兰州 730070

2.兰州交通大学 交通运输学院，兰州 730070

3.甘肃省物流及运输装备信息化工程技术研究中心，兰州 730070

1.Mechatronics Technology and Research Institute,Lanzhou Jiaotong University,Lanzhou 730070,China

2.School of Traffic and Transportation,Lanzhou Jiaotong University,Lanzhou 730070,China

3.Engineering Technology Center for Informatization of Logistics&Transport Equipment,Lanzhou 730070,China

1 引言

交通流量分配是城市交通需求预测与交通网络规划的关键技术，Wardrop平衡分配原则[1]在交通流量分配中被广泛应用，根据该原则的两个平衡原理可以将交通分配问题分为用户均衡（User Equilibrium，UE）和系统最优（System Optiminzation，SO）交通分配问题。Beckmann建立了平衡配流理论的凸数学规划模型[2]，Leblanc首先提出了Frank-Wolfe算法[3]，LeBlanc等通过实例验证了该算法用于交通流量分配的可行性[4]，该算法被认为交通流量分配最经典的算法。Leblanc、Lee和高自友等分别通过搜索步长和搜索方向给出了各种不同的改进Frank-Wolfe算法[5-7]，弥补了原算法存在收敛速度慢的缺陷，使得算法在效率上有了一定的提升。然而，由于Frank-Wolfe算法是一种基于路段（link-based）的方法，无法用于求解OD对间路径的流量。

Leventhal首次提出了基于路径（path-based）的列生成算法（CGA）[8]，认为在每个起终点对之间存在不止一条的最短路径，提出用多条最短路径加载代替全有全无加载，但该算法需要存储大量的路径信息，而且将随着算法迭代次数的增加而变得越来越大，对于大规模交通网络求解变得非常困难。Bar-Gera提出的基于起点的算法（OBA）[9]及Dial提出基于起点的B算法[10]等都是基于路径的交通分配方法，可以求解路径交通量但是不要求储存使用路径，从而不需要占用太多的存储资源，但该算法的有效性还待检验。根据比例一致性条件[11]也可确定路径交通流量，虽然在理论上得到了充分的探讨和验证[12]，Gentile将比例一致性嵌入到基于终点的算法并在VISUM中进行实验可获得唯一路径流量[13]，但目前尚未在实际交通系统中得到验证，也无法证明求解得到的唯一路径流量解是否与实际相符。

Frank-Wolfe算法在每个起终点对之间，反复在最短路径上使用“全有全无”（All Or Nothing，AON）加载方法，不要求太大的存储容量，能将求解非线性规划问题转化为求解一系列的线性规划问题，而且各线性规划具有相同的约束条件，所以该方法具独特的优势。基于Frank-Wolfe算法进行改进用于求解路径交通量也不失为一种有效的尝试。Chen等[14]在2002年提出一种基于OD对的改进Frank-Wolfe算法（OD-Based Frank-Wolfe，ODBFW），在原算法的基础上，针对每个OD对求解相应的下降方向和步长，获取路段流量的同时根据不同OD对的步长时行路段流量的更新，该方法能够有效地求解路径流量值，但由于算法中针对所有OD对求不同的下降方向和步长，对所有的OD间的路径流量要根据新的步长进行更新，会导致计算量大大增加，同时也破坏了Frank-Wolfe原算法的结构；李峰等[15-16]通过将Beckmann的模型进行修改先采用Frank-Wolfe算法计算基于终点的路段交通量，再通过Dijkstra算法得到所有OD对的最短路径集合，然后再根据所提算法确定一组路径交通量，该方法能够有效求解路径交通量，并且经过实例验证，但需要包括Frank-Wolfe算法在内的三个步骤才能求解。

本文提出一种基于Frank-Wolfe算法的改进算法，在不改变Frank-Wolfe原算法结构的前提下，根据每代“全有全无”配流获得的步长更新OD对间所有已配流的路径的交通量，获得路段交通量的同时获得唯一的路径交通量。本文所提算法在不改变Frank-Wolfe原算法结构的前提下，仅通过增加路径流量更新步骤，最终获得路径流量。

2 Frank-Wolfe算法

Beckmann提出的具有固定需求的UE模型[2]如下：

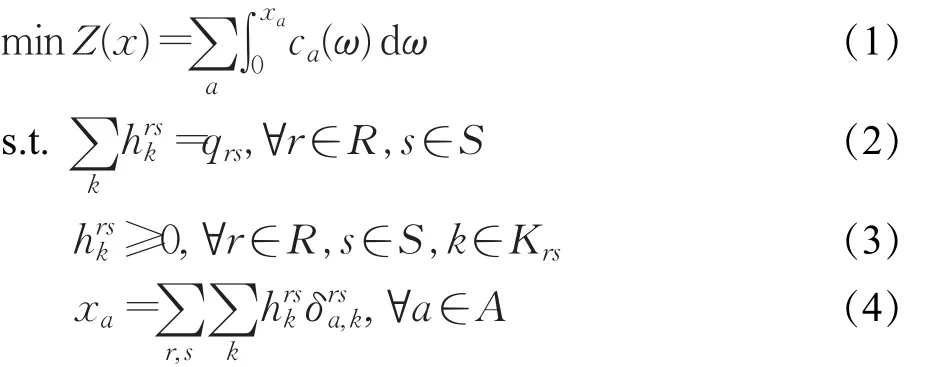
其中A为交通网络中路段的集合，R为产生交通量的起始节点的集合，S为吸引交通量的终讫节点集合，r表示一个起始节点，r∈R，s表示一个终讫节点，s∈S，Krs为连接OD对r-s的所有路径的集合，qrs为所研究时间段内从r到s的交通需求量，为OD对r-s之间第k条路径上的流量，k∈Krs，xa为路段a上的交通流量，a∈A，ca为路段a上的阻抗，表示如果路段a在连接OD对r-s的第k条路径上，其值为1，否则为0。式（1）为目标函数，是所有网络中的路段阻抗函数积分和，式（2）代表路径流量与OD间的交通需求量之间的守衡关系，式（3）保证所有的路径流量一定是正值，式（4）是路段流量与路径流量之间的关联关系。

以下为Frank-Wolfe算法求解步骤：

3 改进Frank-Wolfe算法

在Frank-Wolfe原算法路段流量更新的基础上，对路径流量采用以下方式更新。对于当前代最短路径根据下降步长 αn对路径流量进行修正，在原流量的基础上增加流量，而对于中除路径外的其他已配流路径，在原流量的基础上减少流量，使 r-s间总流量仍保持 qrs。对于中任意路径k，以表示其经过n次迭代后的流量，则路径流量更新方式可采用式（5）表示：

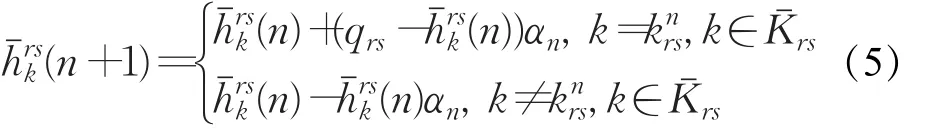
改进后的Frank-Wolfe算法主要在步骤5中增加路径交通量更新步骤，算法步骤如下：

步骤5移动并更新路径流量。

步骤5.2依次检查每一个OD对r，s，更新路径流量。如果，路径上的流量对于其他任意，且，路径 k上的流量，否则，将加入已配流集合，路径上的流量

4 算法复杂度分析

在计算时间复杂度方面，假设交通网络节点个数为n，OD对的个数为g，Frank-Wolfe原算法在求解交通流量分配时的迭代数为l，步骤3中要针对每个OD求最短路径，目前求最短路径比较稳定的算法，如Dijkstra算法，时间复杂度为O(n2)，其他步骤时间复杂度均不超过步骤3，所以对于给定的问题，原算法的时间复杂度为O(gln2)。修改后的步骤5由于要对所有OD已分配流量的路径遍历进行比较，而r-s间所有路径的个数最大为n(n-1)，所以新增部分时间复杂度仍为O(gln2)，因此，增加求解路径交通量步骤后，Frank-Wolfe算法时间复杂度仍为O(gln2)。

5 算例分析

为了验证改进算法的有效性，首先通过一个简单的交通网络流量分配案例中路径交通量的求解来分析一下。对于图1的交通网络（箭头上标示函数为阻抗函数），其中OD间交通需求量为1-4：20，1-3：15，2-4：10，算法采用MATLAB编程实现，设置终止条件ε=0.005，运行过程迭代9次，运行结果如表1所示，流量数据取小数点后四位，交通流量分配结果正确。

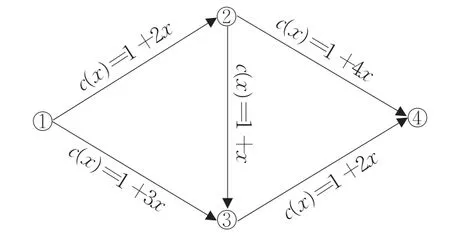
图1 测试网络及阻抗函数

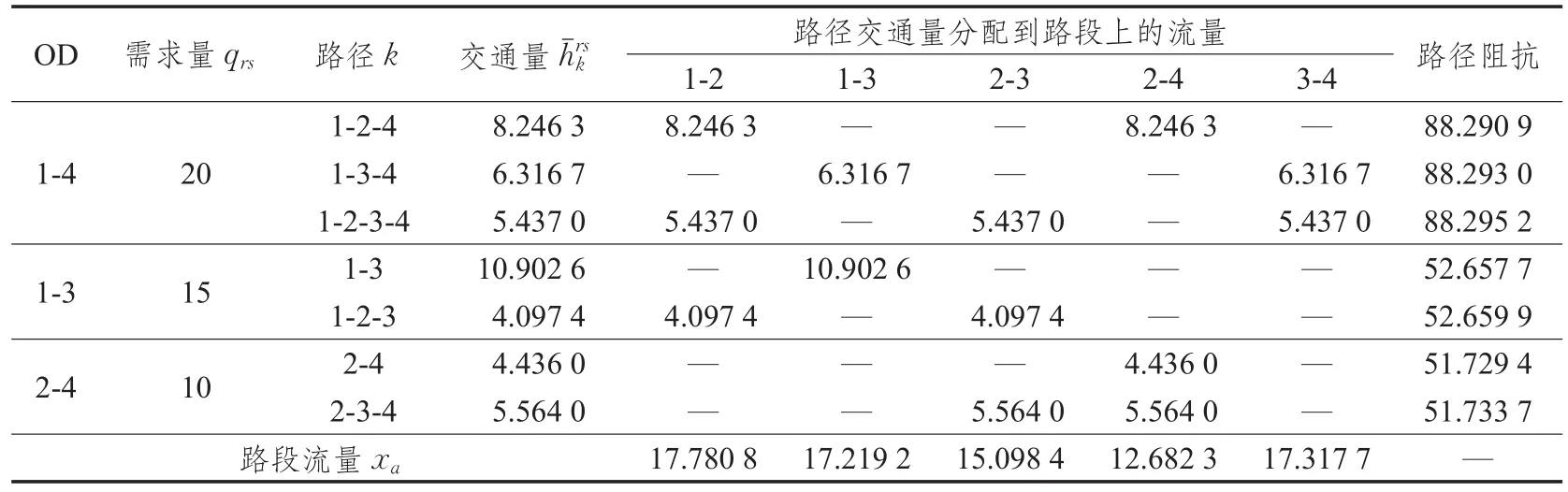
表1 通过改进算法计算所得的路径流量

然后通过MATLAB编程生成较复杂的交通网络（图2）进行实验，采用美国联邦公路局阻抗函数c(x)=t0(1+α(x/c0)β)，其中 t0为自由流时的阻抗，c0为路段通行能力，α、β为回归系数。在编程时以上参数均采用随机方法生成，t0取值范围[0.01，0.1]，c0取值范围[700，800]，α 取值范围为[0.16，0.18]，β 取4，设置终止条件为ε=0.005。

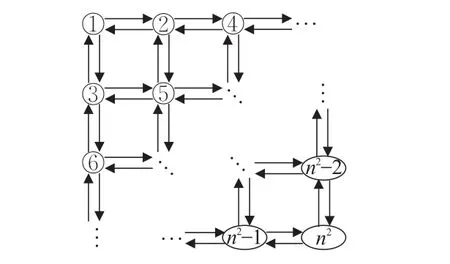
图2 n×n个节点构成的交通网络

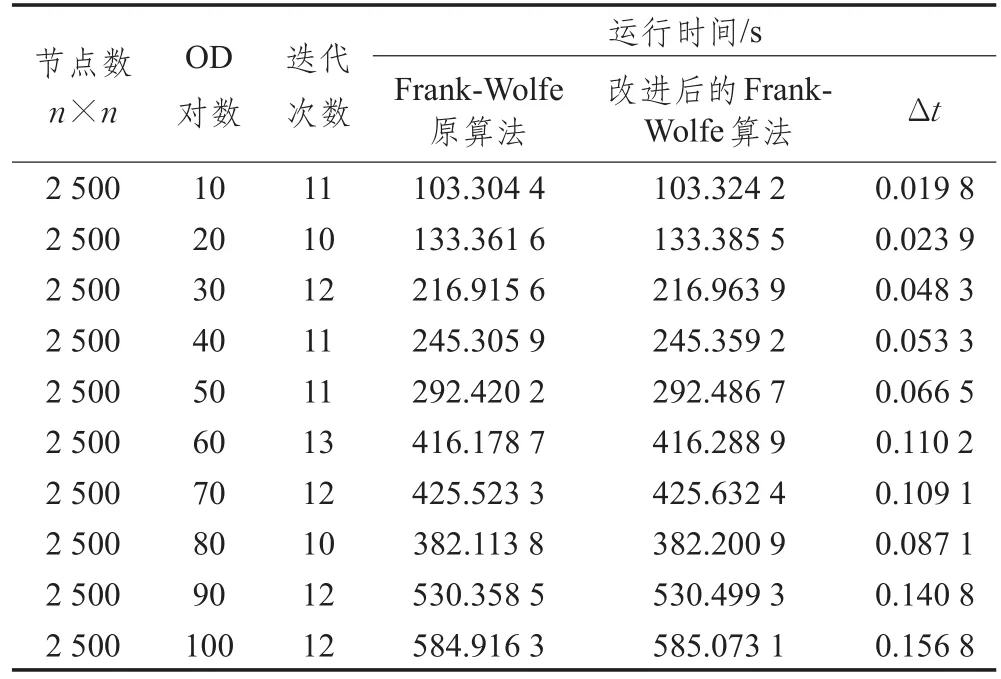
表2 改进行后的算法与原算法运行时间比较（n=50，OD数量从10到100）

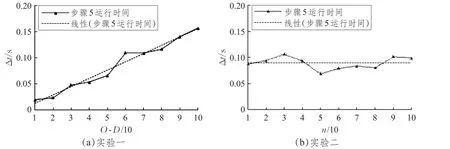
图3 两组实验中步骤5的运行时间

采用改进后的算法，通过MATLAB编程进行以下两组实验来求解路径交通量，Δt表示同等网络结构和O-D对数目下“改进后的Frank-Wolfe算法”与“Frank-Wolfe原算法”运行时间差。（1）n=50时，网络共有2 500个节点和9 800条边，实验中分别随机选取10到100（以10为单位递增）个OD对进行10次计算，获取每个OD各自的路径流量，通过程序运行观察Δt值的变化；（2）n分别取10到100（以10为单位递增），随机选取50个OD对进行10次计算，获取每个OD对各自路径的流量，通过程序运行观察Δt值的变化。运行平台为Intel®Core™ i5-3470 3.20 GHz CPU，4.0 GB内存的个人计算机，程序运行时间如表2和表3所示。设置终止条件为ε=0.005，通过两组实验均能在有限时间内获取所有OD对间的路径流量，通过统计程序中各个步骤的运行时间，改进后的算法较原算法Δt变化趋势如图3所示。

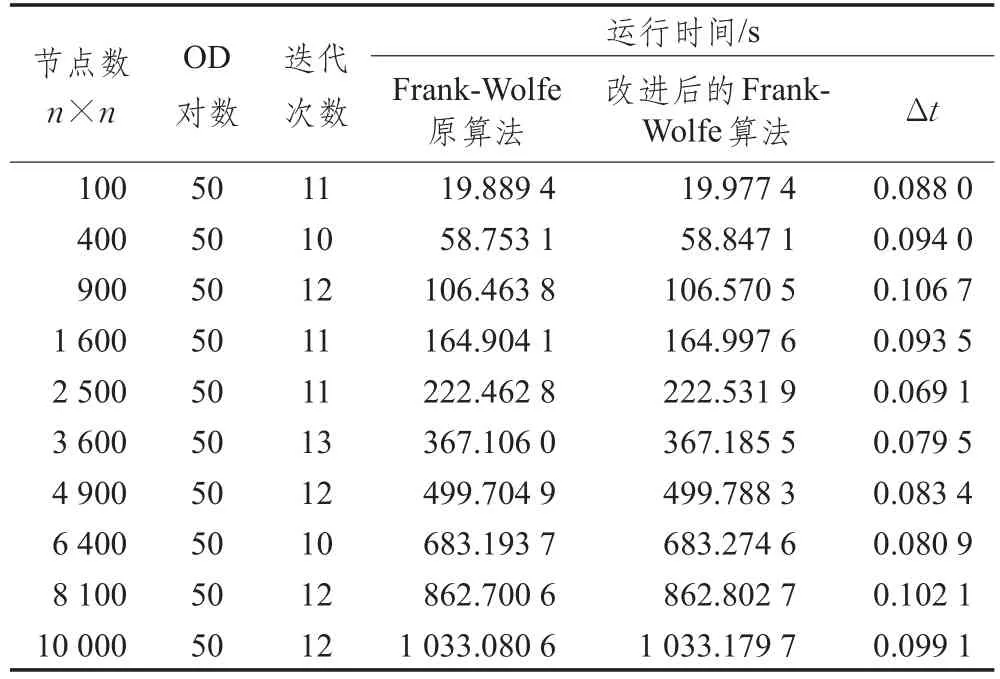
表3 改进行后的算法与原算法运行时间比较（n从10到100，OD数量50）

实验结果表明，在交通网络结构不变的情况下，改进后的算法运行时间与原Frank-Wolfe算法运行时间相比，随着输入OD对数量的增加，Δt随之增大，折线图显示变化趋势接近线性（图3（a））；在OD对的数量不变，交通网络的节点和边的数量增加的情况下，Δt变化不明显，而且接近某个恒定值（图3（b））。同时，由于已配流路径的数量总是小于或等于迭代次数，通过对两组实验中运行时迭代次数分析，已配流路径的数量与节点个数及OD对数的变化关系不明显，改进过程中增加的新变量所需内存的数量并不会随着节点个数及OD对数的增加而大幅增加。

为进一步说明该方法的可行性及有效性，将采用实际的城市交通网络Sioux Falls[4]网络和兰州市主城区交通网络，仍然采用上述实验计算机，分别使用本文所给出的方法和文献[13]所提算法（目前在VISUM中验证过的基于路径交通流量分配算法）对这些网络进行求解，在相同的计算精度(ε=0.005)要求下均能获得路径交通流量，程序运行时间见表4。

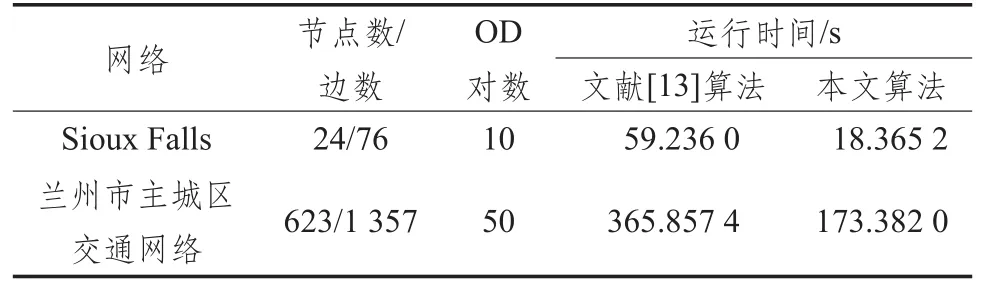
表4 采用实例的计算结果

6 结束语

本文在改进Frank-Wolfe算法的基础上，给出一种路径交通量求解算法，与其他基于路径的交通流量分配求解算法不同，是对基于路段算法的扩展，通过算法分析和算例验证，得出以下结论：

（1）该方法能够避免穷举交通网络中所有路径，利用Frank-Wolfe算法在求解交通流量分配问题上独特的优势，在增加有限的时间与空间成本情况下，计算路段交通流量的同时能够获取路径交通流量。

（2）与Frank-Wolfe原算法相比，在节点及边的数不变，OD对的数量增加的情况时，改进部分的运行时间随OD对数量成线性增加；在OD对的数量不变，交通网络的节点的数量增加的情况时，改进部分的运行时间接近于某一固定值，不会随交通网络节点的增加而增加。

（3）文中算法步骤及算例均针对用户均衡的流量分配，由于算法改进部分不涉及目标函数，所以改进算法仅需修改目标函数后直接用于求解系统最优的流量分配问题。

参考文献：

[1]Wardrop J G.Some theoretical aspects of road traffic research[C]//Proceeding of the Institution of the Institution of Civil Eng，1952：72-73.

[2]Beckmann M J，Mcguire C B，Winston C B.Studies in the economics of transportation[J].Economic Journal，1955，26（12）：820-821.

[3]Frank M，Wolfe P.An algorithm for quadratic programming[J].Naval Research Logistics Quarterly，1956，3（1/2）：95-110.

[4]Leblanc L J，Morlok E K，Pierskalla W P.An efficient approach to solving the road network equilibrium traffic assignment problem[J].Transportation Research，1975，9（5）：309-318.

[5]Leblanc L J，Helgason R V，Boyce D E.Improved efficiency of the Frank-Wolfe algorithm forconvex network programs[J].Transportation Science，1985，19（4）：445-462.

[6]Lee D H，Yu N.Accelerating strategies and computational studies of the Frank-Wolfe algorithm for the traffic assignment problem[J].Transportation Research Record Journal of the Transportation Research Board，2001，1771（1）：97-105.

[7]Gao Z Y，Lam W H K，Wong S C，et al.The convergenceofequilibrium algorithmswith non-monotone line search technique[J].Applied Mathematics&computation，2004，148（1）：1-13.

[8]Leventhal T L，Nemhauser G L，Trotter L E.A column generation algorithm for optimal traffic assignment[J].Transportation Science，1973，7（2）：168-176.

[9]Bar-Gera H.Origin-based algorithm for the traffic assignment problem[J].Transportation Science，2002，36（4）：398-417.

[10]Dial R B.A path-based user-equilibrium traffic assignment algorithm that obviates path storage and enumeration[J].Transportation Research Part B：Methodological，2006，40（10）：917-936.

[11]Bar-Gera H，Boyce D.Route flow entropy maximization in origin-based traffic assignment[C]//14th International Symposium on Transportation and Traffic Theory，1999.

[12]Boyce D，Xie J.Assigning user class link flows uniquely[J].Transportation Research：Part A Policy& Practice，2013，53（3）：22-35.

[13]Gentile G.Local user cost equilibrium：A bush-based algorithm for traffic assignment[J].Transportmetrica，2014，10（1）：1-40.

[14]Chen A，Jayakrishnan R，Wei K T.Faster Frank-Wolfe traffic assignment with new flow update scheme[J].Journal of Transportation Engineering，2002，128（1）：31-39.

[15]李峰，王书宁.基于Frank-Wolfe算法的路径交通量求解方法[J].吉林大学学报：工学版，2005，35（6）：632-636.

[16]李峰，王书宁.基于终点的路径交通量求解方法[J].清华大学学报：自然科学版，2006，46（1）：149-152.