联图K1,1,3∨Cn的交叉数

苏振华

SU Zhenhua

怀化学院 数学系，湖南 怀化 418008

Department of Mathematics,Huaihua University,Huaihua,Hunan 418008,China

1 引言

图G=(V(G),E(G))是简单连通图。将一个图G画在平面上时，若满足如下条件：

（1）任何两条相交叉的边最多交叉一次；

（2）边不能自身交叉；

（3）有相同端点的两条边不交叉；

（4）没有三条边交叉于同一点。

则称此画法为G的一个（好）画法。若图G的一个好画法用D表示，G中所有边与边的交叉数称为在画法D下G的交叉数，用crD(G)表示。图G的交叉数，定义为cr(G)=minD{crD(G)}，其中最小值min取遍G的所有好画法D。若存在G的一个好画法φ满足crφ(G)=cr(G)，则称φ为G的一个最优画法。本文未说明的概念和术语均可参考文献[1]。

图的交叉数是图的一个重要参数，研究图的交叉数有重要的理论意义和现实意义。然而确定图的交叉数是NP-完全问题[2]。目前，只有少数图类的交叉数已经确定[3-7]。1970年Kleitman得到了完全二部图Km,n的交叉数的一个重要结果[4]：

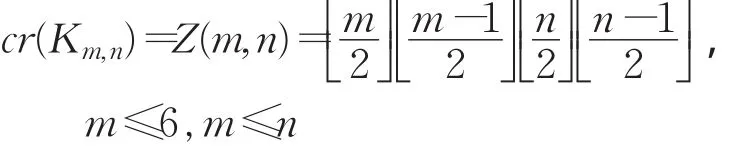
两个点不相交的图G与H的联图，用G∨H表示，是在G与H的并图中，把G的每个顶点与H的每个顶点连接起来所得到的图。目前，关于联图的交叉数的研究。Oporowski等人在文献[8]中得到了联图C3∨C6的交叉数。2007年Klesc[9]和唐玲[10]分别独立地确定了联图 Pm∨Pn，Cm∨Pn，Cm∨Cn的交叉数。2010年Klesc[11]证明了一个特殊六阶图与路、圈的联图交叉数。2011年Klesc[12]得到了所有4阶图G 与路Pn，圈Cn的联图的交叉数，特别地得到了cr(K1,1,2∨Cn)=Z(4,n)+。袁秀华[13]研究了联图K2,3∨Cn的交叉数。文献[14]得到了完全图K1,1,3与路Pn的联图交叉数，并给出了目前已知的五阶图与路的联图交叉数结果。2014年岳为君等[15]得到了联图W4∨Cn的交叉数。

为与相关文献保持一致，用Pn表示n个顶点的路，Cn表示长为n的圈。本文在Klesc给出的联图K1,1,2∨Cn的交叉数为的基础上，根据唐玲[10]和Klesc[11]得到的关于Cn联图交叉数的相关性质，运用反证法和排除法，得到了联图 K1,1,3∨Cn与{K1,1,3+e}∨Cn的交叉数均为

2 性质与引理

性质2.1[5]设D为图G的一个好画法。若A、B、C是图G的三个互不相交的边子集，则有：

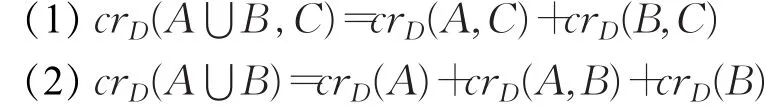
性质2.2[14]（1）若H 与G同构，则cr(H)=cr(G)；

（2）若H 是G的子图，则cr(H)≤cr(G)；

（3）设D是G的一个好画法，则cr(G)≤crD(G)。

引理2.4[10]设G为任意图，若D为图G∨Cn的一个最优画法，则圈Cn自身不发生交叉，即crD(Cn)=0。

引理2.5[11]设D为图mK1∨Cn的一个好画法，若Cn自身不交叉，且不与其他边交叉，若m个顶点位于圈Cn所形成的区域内，则对所有的Ti与Tj(i≠j)，有

3 K1,1,3∨Cn的交叉数

为了方便，首先对K1,1,3∨Cn作如下标记：V(K1,1,3∨Cn)={t1,t2,…,t5}⋃{v1,v2,…,vn}，Ti(1≤i≤5)为 K1,1,3的顶点ti与vj(1≤j≤n)相连边的导出子图。则有：

证明 当n=3时，K1,1,3∨C3同构于联图K5∨3K1，由引理2.1及性质2.2可得：cr(K1,1,3∨C3)=cr(K5∨，结论成立。下面的证明仅需考虑n≥4的情形。

由图1，K1,1,3∨Cn的一个好画法，通过计数与性质2.2可得。下面只需证明对任意的好画法φ，均有成立即可。现假设存在K1,1,3∨Cn的一个最优画法D，使得：

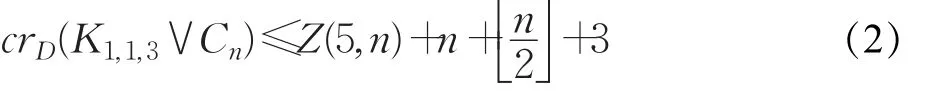
图1 K1,1,3∨Cn的一个好画法

断言1圈Cn的每条边最多有1个交叉。

否则若有2个交叉发生在Cn的同一边上，则删除Cn的这条边，得到一个同构于K1,1,3∨Pn的子图，由性质 2.1，2.2 及 引 理 2.3，有。与假设式（2）矛盾。

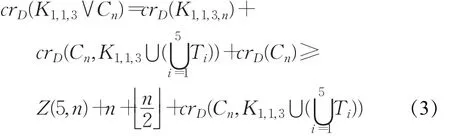
其次若。因为K1,1,3为2-边连通图(crD(Cn,K1,1,3)≥2)，所以只可能是删除Cn中与相交的那条边，得到的图同构于K1,1,3∨Pn，因此有，与引理2.3矛盾。

下面根据断言2分4种情形讨论。

子情形1.1 K1,1,3的5个顶点均位于Cn的同一（内部或外部）区域，且

子情形1.2 K1,1,3的1个2-度点，不妨设为t1，位于Cn的内部区域，则K1,1,3的其余4个顶点均位于Cn的外部区域（如图2（a）所示）。根据K1,1,3的结构，存在连接t2、t3的边，t1、t2、t3构成3-圈，且 t1、t2、t3的两交叉边之间至少存在一个顶点v。因此

（1）若crD(K1,1,3)=0。则K1,1,3画法唯一。因此在图2（a）中，不论 t4、t5，位于 t1t2t3内部或外部区域，均有crD(T4⋃T5,K1,1,3)≥4。因此有，与式（2）矛盾。

图2 不同情况下Cn与发生的交叉图

（2）若 crD(K1,1,3)≥1 。在图2（a）中，不论 t4、t5，位于t1t2t3内部或外部区域，均有crD(T4,K1,1,3)≥1,crD(T5,K1,1,3)≥1。因此有，与式（2）矛盾。

子情形2.1 K1,1,3的5个顶点均位于Cn的同一（内部或外部）区域，且不妨设crD(Cn,T1)=1。对2≤i＜j≤5，根据引理2.5可得因此有。矛盾。

子情形2.2 K1,1,3的1个2-度点，不妨设为t1，位于Cn的内部区域，其余4个顶点均位于Cn的外部区域（如图2所示）。根据 K1,1,3的结构，存在t2、t3与t1构成3-圈。

（1）若 crD(Cn,T1)=1。则Cn与 K1,1,3及T1发生3个交叉如图2（b）所示。不论t4、t5，位于t1t2t3内部或外部区域，均有crD(T4⋃T5,K1,1,3)≥2，crD(T4⋃T5,T1)≥2。因此有，矛盾。

（2）若 crD(Cn,T2)=1或 crD(Cn,T3)=1。不妨设crD(Cn,T2)=1。根据画法的定义及断言1，Cn与K1,1,3及T2发生的3个交叉如图2（c）所示。则有1。因此有，矛盾。

（3）若crD(Cn,T4)=1或crD(Cn,T5)=1。不妨设crD(Cn,T4)=1 。若 t4位于 t1、t2、t3内部区域，则 crD(T3,K1,1,3)≥1,crD(T4,K1,1,3)≥2，crD(T5,K1,1,3)≥2，crD(T1,T4)≥1。因此有，矛盾。

若 t4位于 t1、t2、t3外部区域，则交叉情况如图2（d）所示。且根据图K1,1,3的结构，t2与t4之间有边相连。则有crD(T1,T4)≥1,crD(T4,K1,1,3)≥1，crD(T3,K1,1,3⋃t4vi)≥1，若crD(K1,1,3)=0，则有crD(T5,K1,1,3⋃t4vi)≥3；若crD(K1,1,3)≥1，则crD(T5,K1,1,3⋃t4vi)≥2。因此总有：，矛盾。

子情形3.1存在一点，不妨设为t1，满足crD(Cn,T1)=2。根据引理2.4，cr(Cn)=0。G的5个顶点全部位于Cn所分的一个（内部或外部）区域内，不妨设为外部区域。

（1）当n=4时。根据画法的的定义及断言2.1，只能是T1的两条边与C4的两条边产生2个交叉（T1的一条边与C4的两条边各产生1个交叉时，与画法的定义矛盾），相关图形如图3（a）所示。显然不论K1,1,3的另外4个顶点位于Cn外部的哪个区域，对2≤i≤5，有crD(Ti,T1)≥2。由引理2.5，对2≤i＜j≤5，有cr(Ti,Tj)≥因此，矛盾。

图3 不同情况下Cn与发生的交叉图

（2）当 n≥5时。由引理 2.5，对 2≤i＜j≤5，有。因此有。矛盾。

子情形3.2存在两点，不妨设为t1、t2，满足crD(Cn,T1)=crD(Cn,T2)=1。

Cn将平面分成内外两个区域，不妨设K1,1,3的5个顶点全部位于Cn的外部区域。根据画法的定义及断言1，只能是T1、T2分别与Cn的两边分别交叉，不妨设两交叉点为 x1、x2，如图3（b）所示。根据 K1,1,3的构造，任意两个顶点t1、t2之间均有路连接，因此路t1t2把Cn的外部区域分成t1t2x2x1内部和外部两个区域，不论K1,1,3的另外3个顶点位于哪个区域，对3≤i≤5，均有。对T1、T2，有。因此，矛盾。

子情形4.1存在一点，不妨设为t1，满足crD(Cn,T1)=3。

根据画法的定义及断言1，T1与Cn产生3个交叉时，Cn至少有5个以上顶点（否则不满足题设条件）。由引理5，对2≤i＜j≤5，有。因此，矛盾。

子情形4.2存在两点，不妨设为t1、t2，满足

根据画法的定义及断言1，T1、T2与Cn的交叉只可能如图3（c）所示，且Cn至少有5个以上顶点。因为两个交叉之间至少有一个顶点，所以T1与Cn的两个交叉之间至少存在一个点，则对3≤i＜j≤5，有cr(Ti,T1)≥。因此，矛盾。

子情形4.3存在3点，不妨设为t1、t2、t3，满足

根据画法的定义及断言1，T1、T2、T3与 Cn的交叉只可能如图3（d）所示，且Cn至少有5个以上顶点。因为任意两个顶点之间均有路相连，则t1、t2、t3之间均有路相连。对4≤i＜j≤5，不论ti位于哪个区域，均有cr(Ti,T1⋃且有因此4(n≥5)，矛盾。

综合上述4种情形，假设式（2）不成立。因此对任意的好画法 φ ，均有成立。定理得证。

4 {K1,1,3+e}∨Cn的交叉数

在图K1,1,3，3个2-度点之间任意连接一边e，可得到图K1,1,3+e。有下面的定理。

证明 首先构造{K1,1,3+e}+Cn的一个好画法如图4所示，显然有其次根据K1,1,3+Cn⊆{K1,1,3+e}+Cn，则由定理3.1及性质2.2可得。定理证毕。

图4 {K1,1,3+e}+Cn的一个好画法

5 结束语

本文在Klesc给出联图K1,1,2∨Cn的交叉数为Z(4,n)+的基础上，根据联图的相关性质，运用反证法和排除法得到了联图K1,1,3∨Cn的交叉数为Z(5,n)+n+，并假设在Zarankiewicz猜想成立的前提下，根据本文的证明，给出了对K1,1,m∨Cn(m≥4)的交叉数的一个猜想：

长期以来，计算图的交叉数问题研究主要采用纯数学方法。但是，随着所研究图的阶数增大，可能的画法急剧增长，研究也越来越困难，如对完全图的研究，从n=10进展到n=12，花了整整30年的时间。因此，随着计算机技术突飞猛进的发展，利用计算机辅助计算图的交叉数是一种必然的趋势。这也是各研究者今后一段时间内面临的极具挑战性的工作。

参考文献：

[1]Bondy J A，Murty U S R.Graph theory with applications[M].North-Holland：Elsevier Science Ltd，1976.

[2]Garey M R，Johnson D S.Crossing number is NP-complete[J].Slam J Algebric Discrete Methods，1993，4：312-316.

[3]黄元秋，王晶.图的交叉数综述[J].华东师范大学学报：自然科学版，2010（3）：68-80.

[4]Kleitman D J.The crosing number ofK5,n[J].J Graph Series B，1970，9：315-323.

[5]Pak T H.The crossing number of K1,1,3,n[J].ARS Combinatoria，2011，99：461-471.

[6]Klesc M.The crossing number of Cartesian products of paths with 5-vertex graphs[J].Discrete Mathematics，2001，233：353-359.

[7]Lv S X，Huang Y Q.On the crossing numbers of K5×Sn[J].Journal of Mathematical Research Exposition，2008，28（3）：445-459.

[8]Oporowski B，Zhao D.Coloring graphs with crossing[J].Discrete Mathematics，2009，309：2948-2951.

[9]Klesc M.The join of graphs and crossing numbers[J].Electronic Notes in Discrete Math，2007，28：349-355.

[10]Tang Ling，Wang Jing，Huang Yuanqiu.The crossing numberofthejoin ofCmandPn[J].International Journal of Mathematical Combinatorics，2007，1：110-116.

[11]Klesc M.The crossing numbers of join of the special graph on six vertices with path and cycle[J].Discrete Mathematics，2010，310：1475-1481.

[12]Klesc M.The crossing numbers of join products of path with graphs of order four[J].Discussiones Mathematicae Gragh Theory，2011，31：321-331.

[13]袁秀华.K2,3∨Cn的交叉数[J].华东师范大学学报：自然科学版，2011（5）：21-24.

[14]苏振华，黄元秋.五阶图与路Pn的联图交叉数[J].高校应用数学学报，2014，29（2）：245-252.

[15]岳为君，黄元秋，欧阳章东.联图W4∨Cn的交叉数[J].计算机工程与应用，2014，50（18）：79-84.