一种全面响应时间的频率稳定度测量
许龙飞, 罗 丹, 周 渭, 白丽娜, 李智奇, 苗 苗
(西安电子科技大学 机电工程学院,陕西 西安 710071)
一种全面响应时间的频率稳定度测量
许龙飞, 罗 丹, 周 渭, 白丽娜, 李智奇, 苗 苗
(西安电子科技大学 机电工程学院,陕西 西安 710071)
为从本质上反映不同频率源的频率稳定度随响应时间的变化规律,提出了一种可以测量全面响应时间的频率稳定度的方法.该方法在数字环境下,应用数字边沿效应抑制量化误差,并结合数字双混频时差法测量信号间的相位差,通过相位差得到全面的频率稳定度指标.实验证明,该方法在自校的条件下,100ns的频率稳定度能够达到10-5,秒级稳定度能够达到10-12,一天的频率稳定度能够达到10-16.
数字化;量化误差;双混频时差;频率稳定度
频率稳定度按照响应时间的大小分为瞬态频率稳定度[1]、短期频率稳定度和长期频率稳定度.传统的频率稳定度测量方法有很多,例如有通过相位差测量的相位重合法、时间间隔测量和双混频时差法,有通过频率测量的差拍法、频差倍增法以及模拟内插法等[2-5].这些测量方法大都基于闸门计数,只能测量毫秒及以上的频率稳定度,并且大都在模拟的环境通过计数闸门进行测量,虽然能达到一定的测量精度,但是存在单点过零检测对噪声较为敏感、对线路性能要求严格以及线路分辨率有限等问题,并且由于计数闸门无法太短,导致无法得到其更短时间的频率稳定度指标,而这些更短时间的频率稳定度的测量对于频率源的抖动、实时短期不稳定度以及远端相位噪声的描述具有重要的作用.针对这些情况,笔者提出了在数字平台下进行相位差测量的方法,将模拟信号通过模/数转换器转变成数字信号,对模/数转换器的采样时钟频率进行控制,使得到的数字信号具有数字模糊区,应用数字边沿效应抑制量化误差,并结合双混频时差算法得到信号间的相位差,进而得到频率稳定度.将模拟信号转换成数字信号之后,用的是鉴相算法,能得到信号间的相位差,弥补了模拟平台下计数闸门无法太短的不足,因此能够得到更加全面的频率稳定度.对频率源全面的频率稳定度随响应时间的变化规律掌握,可以从本质上区分频率源的相位或者频率控制,这也是对频率源进行改进所必须要掌握的技术.

图1 c=1时两信号的相位变化关系
1 信号间的特殊相位关系
设两信号的频率分别为fA和fB,其中fB=cfA+ Δf(Δf≪fA),随着时间的延伸,两信号间的相位关系有特殊的变化规律.c=1 时两信号的相位差的变化规律如图1所示.
图1中Δt表示两信号之间的相位差,Δt=TA-TB;Tmin为两信号的最小公倍数周期[6].假设图中初始时刻两信号的上升沿完全重合,以后每经过一个TA,两者的上升沿之间的距离会相对变化Δt,即两者之间的相位差会增加或减少Δt,经过1个Tmin后,两者之间的相位差累积成一个周期TB,这时两比对信号的上升沿又会重新完全重合,并重复之前的变化规律.
若c≠1,则可将cfA看成一个整体,其变化规律可以归结到c=1的情况.
2 数字边沿效应和量化误差的抑制
将信号间的特殊相位关系运用到模/数转换器的采样过程中,经过简单的处理,能抑制很大一部分量化误差.模/数转换器的采样分为过采样和欠采样,这里只详述欠采样.过采样的原理和欠采样的类似.
设模/数转换器的位数为N位,测量量程为Ucc,则模/数转换器的分辨率为Ucc/ (2N-1).设模/数转换器的输入信号y(t)=Ucsin(2πfAt+β(t)),采样频率为fB(fB=fA+ Δf,Δf≪fA).模/数转换器的采样过程如下:
y(nTB)=Ucsin(2πfAnTB+β(nTB)) ,
(1)
其中,TB为采样周期,TB=1/fB,n=1,2,3….将fB=fA+Δf代入式(1)中,得到
(2)

(3)
从式(3)中可以看出,模/数转换器输入的是频率为fA的信号,经过模/数转换器量化后,输出的是频率为Δf(Δf=fB-fA)的信号,这样模/数转换器相当于输入为fA和fB的数字化的混频器和低通滤波器.
结合信号间的特殊相位关系和模/数转换器的采样过程,每经过一个模/数转换器的输入信号周期TA,采样时钟信号和模/数转换器的输入信号的上升沿会相对拉开Δt,所对应的两个采样点之间的幅度增加Δu,Δu的大小为
Δu=y((m+1)TB)-y(mTB) ,
(4)
其中,m为大于零的正整数.式(4)化简得到
Δu=y(mTB+TA-Δt)-y(mTB)=y(mTB-Δt)-y(mTB) .
(5)
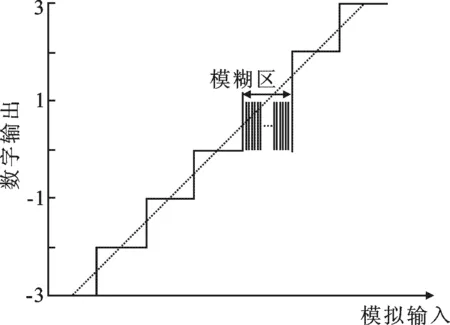
图2 数字模糊区
如果Δu 图2中的横轴表示模/数转换器的模拟输入,纵轴表示模/数转换器的数字输出.由图2可知,每个数字模糊区由许多个等间隔的量化值相同的点组成,每个模糊区中间都存在一个与真值相差最小的点.同一个数字模糊区中每两个相邻点之间的实际幅度大小相差Δu,因此,可以对模糊区中的点依次标号,模糊区的边沿标号为1,其他依次增加,以这样的方式补偿来提高模/数转换器的分辨率.或者直接取边沿(跳变的点),加上一个固定的补偿,这就是数字边沿效应.利用数字边沿可以取到真实值或者接近真实值的点,从而抑制量化误差.这样得到的数字信号虽然频率与原信号不同,但是幅度与原信号一样,仅仅是在横坐标上相差一个倍数.如果将所有的点按照量化值依次重新进行排列,则可恢复出原信号. 在短期和长期频率稳定度的测量中,并不需要取所有的采样点进行量化误差的处理,而是根据信号间最小公倍数周期的大小只取信号过零点附近的采样点进行处理,原因是计算频率稳定度并不需要每个采样点的相位差,并且过零点区域的点不仅仅可以消除线性误差,而且在过零点区域的点的变化斜率最大, 模/数转换器所对应的相位分辨率最高.而在瞬态稳定度的测量过程中,可以使Δf尽量小,这样就能保证在信号过零点附近有更多的采样点. 传统的数字双混频时差方法中存在数字混频[7-8]、抽取滤波、直接数字合成器(Directed Digital Synthesizer,DDS)和鉴相等算法,处理流程十分复杂,而且会有精度损失.文中对双混频时差进行了改进,直接在模/数转换器采样过程中应用特殊频率信号间的特殊相位规律进行量化和量化误差处理,然后直接鉴相,得到信号间的相位差,系统如图3所示.图3中主要分为模拟部分和数字部分,模拟部分主要是模/数转换器输入通道的设计,主要实现对信号进行滤波和采样以及消除噪声干扰.在印制板走线上设计成差分对,布局上各通道之间相互对称,可以降低噪声干扰.数字部分的算法在现场可编程门阵列(Field Programmable Gate Array,FPGA)和单片机中实现.模/数转换器输出的数字信号先经过一个拟高斯滤波器[9],主要是消除一部分模/数转换器的随机噪声,然后利用数字边沿效应进行量化误差的抑制.象限判断用一个一定长度的先进先出的队列实现,判断队列两头和中间数据的大小来判断数据的象限.反正弦鉴相算法用查找表实现,因为实验只取过零点区域的采样点,因此可节约FPGA很大一部分逻辑资源.鉴相之后得到的是信号的角度,然后利用双混频时差原理得到两信号之间的相位差,发送给单片机进行频率稳定度的计算.根据前面所述,模/数转换器可以作为一个数字化的混频器和低通滤波器,因此,图中的数字部分实际上是一个中介源为采样时钟的数字化的双混频时差系统. 图3 频率稳定度测量系统 假设被测信号yx(t)=Axsin(2πf0t+βx(t)),参考信号y0(t)=A0sin(2πf0t+β0(t)),时钟采样频率fs=f0+ Δf(Δf≪f0),根据上面所述,模/数转换器相当于数字化的混频器和低通滤波器,经过模/数转换器采样之后,模/数转换器输出频率为Δf的数字信号,其瞬时相位分别为 (6) 根据双混频时差原理,得到被测信号和参考信号的相位差为 (7) 其中,Xx0为被测信号和参考信号之间的相位差,Xx0b为两模/数转换器输出数字信号间的相位差,φx和φ0分别为被测信号和参考信号的瞬时相位,φxb和φ0b分别两模/数转换器输出的数字信号的瞬时相位. 实验采取图3中的方案,模/数转换器的分辨率为16 bit,以8607-BE 10 MHz OCXO晶振作为罗德史瓦茨SMB100A信号发生器的外部参考输入,罗德史瓦茨SMB100A信号发生器产生 (10 MHz+ 10 Hz) 频率的信号,作为 模/数转换器的时钟信号fs,1 s 以下的频率稳定度用铷钟输出 10 MHz 信号作为被测信号,用8607-BE OCXO晶振输出的 10 MHz 信号作为参考信号;1 s 以上的频率稳定度用铯钟输出 10 MHz 信号作为参考信号,用铷钟输出 10 MHz 作为被测信号,模/数转换器的采样时钟不变.实验开始时,先分别利用特殊频率信号间的特殊相位规律测出被测信号和参考信号的幅度,并储存;然后利用数字模糊区的边沿抑制量化误差,用双混频时差法测出信号间的相位差,得到的频率稳定度曲线如图4所示. 图4中纵坐标表示频率稳定度,用阿伦方差表示.数据处理用计算频率稳定度的专用软件stable32进行.从图4可以看出,100 ns 的稳定度能够达到 2.92× 10-5,1 s 的稳定度能到达 1.82× 10-11.图4中铷原子钟的频率稳定度曲线在 100 ns 和数十毫秒之间随取样时间呈 1/τ规律变化,数十毫秒以上的频率稳定度变化规律随着取样时间就靠向了 1/τ1/2的变化规律.这是因为实验中所用铷原子钟中的晶体振荡器本身的频率稳定度是按照 1/τ的规律变化的,但是铷原子钟存在一个调制信号,由于物理部分的锁频作用,在数十毫秒以上的频率稳定度变化规律随着取样时间就靠向了 1/τ1/2的规律变化. 图4 铷钟的频率稳定度图图5 高稳晶振自校频率稳定度图 以8607-BE 10 MHz OCXO晶振作为泰克信号发生器的外部参考输入,泰克信号发生器产生 (10 MHz+ 10 Hz) 频率的信号,作为模数转换器(Analog to Digital Converter,ADC)的时钟信号fs,参考信号和被测信号都采用8607-BE 10 MHz OCXO晶振输出的 10 MHz 频率信号,得到的结果如图5所示. 图5的数据处理用计算频率稳定度的专用软件stable32进行.在长期比对中,一天的频率稳定度能到达 4.38× 10-16,并且随取样时间呈 1/τ规律变化. 文中描述了一种数字的全面的频率稳定度测量方法,该方法结合了数字双混频时差和数字边沿效应的特点,使用低速、低分辨率的模/数转换器实现高精度的测量,并且随着所用模/数转换器分辨率的提高,测量精度也会有一定的提高.经过实验证明,这种方法测得的瞬态稳定度能够达到 10-5/100 ns ,短期稳定度能够达到 10-12/s,长期稳定度能够达到10-16/d. 参考文献: [1] 白丽娜, 周渭, 惠新明, 等. 频率标准瞬态稳定度的精密测量[J]. 西安电子科技大学学报, 2014, 41(2): 102-106. BAI Lina, ZHOU Wei, HUI Xinming, et al. Precise Measurement of the Transient Stability of Frequency Standards[J]. Journal of Xidian University, 2014, 41(2): 102-106. [2] ZANETTE D H. Frequency Stabilization by Synchronization of Duffing Oscillators[J]. Europhysics Letters, 2016, 2(115): 20009. [3] 偶晓娟, 周渭, 易韦韦, 等. 精密频率测量边沿效应的特性分析[J]. 西安电子科技大学学报, 2016, 43(3): 144-148. OU Xiaojuan, ZHOU Wei, YI Weiwei1, et al. Characteristic Analysis of the Border Effect in Precision Frequency Measurement[J]. Journal of Xidian University, 2016, 43(3): 144-148. [4] PROCHAZKA I, PANEK P, KODETJ. Precise Phase and Frequency Comparator Based on Direct Phase-time Measurements[J]. Review of Scientific Instruments, 2014, 85(12): 126110. [5] BRIDA G. High Resolution Frequency Stability Measurement System[J]. Review of Scientific Instruments, 2002, 73(5): 2171. [6] BAI L N, SU X, ZHOU W, et al. On Precise Phase Difference Measurement Approach Using Border Stability of Detection Resolution[J]. Review of Scientific Instruments, 2015, 86(1): 015106. [7] 王正明, 董绍武, 刘春侠, 等. NTSC的双混频时差测量系统试运转结果分析[J]. 时间频率学报, 2006, 29(2): 134-141. WANG Zhengming, DONG Shaowu, LIU Chunxia, et al. Test Running and Data Analysis on the Dual Mixer Time Difference System at NTSC[J]. Journal of Time and Frequeney, 2006, 29(2):134-141. [8] 赵科佳, 张爱敏, 徐清华, 等. 数字式双混频时差测量系统的试验研究[J]. 仪器仪表学报, 2014, 35(12): 2858-2865. ZHAO Kejia, ZHANG Aimin, XU Qinghua, et al. Experimental Research on Digital DMTD Measurement System[J]. Chinese Journal of Scientific Instrument, 2014, 35(12): 2858-2865. [9] 周翠. 基于FPGA的高斯滤波器的快速实现[J]. 空军雷达学院学报, 2011, 2(3): 186-188. ZHOU Cui. Fast Implementation of Gaussian Filter with FPGAs[J]. Journal of Air Force Radar Academy, 2011, 2(3): 186-188. Methodofacomprehensiveresponsetimeoffrequencystability XULongfei,LUODan,ZHOUWei,BAILina,LIZhiqi,MIAOMiao (School of Mechano-electronic Engineering, Xidian Univ., Xi’an 710071, China) To reveal the change of the frequency stability of a different frequency source with the response time in essence, a method of measuring the comprehensive response time of frequency stability is proposed. In the digital environment, the digital edge effect is used to inhibit the quantization error, combined with the digital double mixing time difference method to measure the phase difference between the signals, by which the comprehensive frequency stability index is obtained. In experiments, the frequency source realizes the frequency stability of a more comprehensive change rule over time. Experiment proves that the method under the condition of self-calibration, transient frequency stability can be 10-5/100 ns, that short-term frequency stability can be 1012/s, and that frequency stability for a long time can be 1016a day. digital;quantization error;double mixing time difference;frequency stability 2017-03-04 时间:2017-06-29 国家自然科学基金资助项目(11773022);陕西省重大科技成果转化引导专项资助项目(2015KTCG-01) 许龙飞(1990-),男,西安电子科技大学硕士研究生,E-mail: 18710849321@163.com. http://kns.cnki.net/kcms/detail/61.1076.TN.20170629.1734.026.html 10.3969/j.issn.1001-2400.2018.01.013 TM935.12 A 1001-2400(2018)01-0072-04 (编辑: 齐淑娟)3 频率稳定度测量系统

4 实验论证和误差分析

5 结 束 语

