WSN中基于双群体差分进化的资源分配优化算法

郝晓辰，王立元，刘金硕，解力霞，张文焕

（燕山大学电气工程学院，河北 秦皇岛 066004）

1 引言

无线传感器网络（WSN,wireless sensor network）是由部署在监测区域内大量相互通信的传感器节点形成的多跳自组织网络[1]。随着 WSN节点数目的不断增加，节点受到的干扰以及链路之间的通信冲突也会随之增强，这不仅会造成网络容量下降，还会导致网络中的节点由于数据重传浪费能量。因此，如何进行合理地资源分配使网络在降低干扰和避免通信冲突的同时，增加网络容量、降低节点能耗成为亟待解决的问题。

传统的资源分配都是单独进行的，例如，文献[2]研究了单独的信道分配技术，其算法能够明显降低网络的干扰。时隙分配问题也是当前研究的热点问题[3～6]，时隙分配是避免通信链路冲突的最有效方法。但是单独的信道分配或时隙分配都只能对网络的某一方面性能进行优化，并且这种优化可能是在牺牲另一方面性能的基础上的。基于这种考虑，许多研究者开始致力于资源分配联合优化的研究，张治学等[7]考虑了信道分配与时隙分配对网络性能的影响，提出了信道分配与时隙分配的联合优化算法，但是该算法只是对以上2种算法的简单叠加，并没有真正考虑到它们之间的交互关系，这造成资源的严重浪费。文献[8]在此基础上考虑了信道分配与时隙分配之间的相互影响关系，采用优化的多信道分配机制，实现了时隙重用与信道数优化。文献[9～12]都是对信道分配和功率控制进行了联合优化，并在一定程度上对已有的工作做出了一些改进。文献[13]提出了基于标准差分进化的信道分配与功率控制算法，然而该算法并没有考虑节点能量的局限性，也没有考虑可能存在的链路冲突对网络造成的干扰。文献[14]针对多信道多接口多跳的无线传感器网络提出了联合拥塞控制、信道分配以及链路调度的算法。以上研究中并没有一种算法是联合研究信道分配、功率控制和时隙分配问题的，此外，以上研究都是把所求问题通过加权的方法转化为单目标优化问题，使用这种方法得到的结果对权重的依赖性较大，权重因子的选择往往就能决定结果的偏向。

基于上述分析，为提高多射频多信道无线传感器网络的性能，提出了基于多目标优化模型的联合资源分配算法，主要贡献如下。

1) 综合考虑了信道分配、功率控制以及时隙分配之间相互影响的关系，构建了系统的干扰模型和链路容量模型。

2) 以链路的干扰和冲突为约束条件，以减小能耗、增大网络容量以及提高资源分配的均衡性为目标函数，构建了系统的资源分配多目标优化模型。多目标优化模型的建立突出了不同目标之间的权衡。

3) 采用双群体差分进化算法对本文所构建的模型进行求解，并与使用标准差分进化算法的结果进行对比，实验结果表明本文算法对提升网络各方面的性能都有很大的改进。

2 干扰模型和链路容量

一般而言，节点的接口数目小于信道的个数，且节点的接口可以在各信道间进行切换。针对无线传感器网络的特点，本文有以下假设。

1) 节点的接口可以在各个信道及功率等级上进行切换，但在一个时隙内只能使用一个信道及一个功率等级。

2) 时隙的长度都是相同的，连续的时隙集合组成一个周期，成为帧结构，本文在研究过程中不考虑时隙的长短而只考虑时隙的个数对网络性能的影响。

无线传感器网络用有向图 G=(V,E)表示，其中，V表示节点集，E为边集，设网络中有N个节点，L条链路，则 V ={1,2,…,N},E={1 ,2,…,L},用Mi表示节点i的接口个数，任意一条链路eij∈E表示节点i到节点j的单向链路。网络中信道集合用 C={1,2,… ,K }表示，K为可用信道的个数，所需的时隙集合用 R={1,2,… ,S }表示，S为最终为网络分配的时隙个数，每条链路的可选功率范围为是能够使链路 eij正常通信的最小发射功率,根据信噪比定义[13]，可以得到满足信噪比条件的链路 eij的最小发射功率为其中， hij是链路增益，α表示路径损耗系数。 pmax(eij)是各节点的最大发射功率。只有当各链路的接收节点信噪比大于给定阈值时才能成功接收到消息，因此，本文用信噪比来描述链路受到的干扰强度大小，链路eij在信道 cij、时隙 rij中正常传输时，链路 eij的接收节点信噪比可表示为

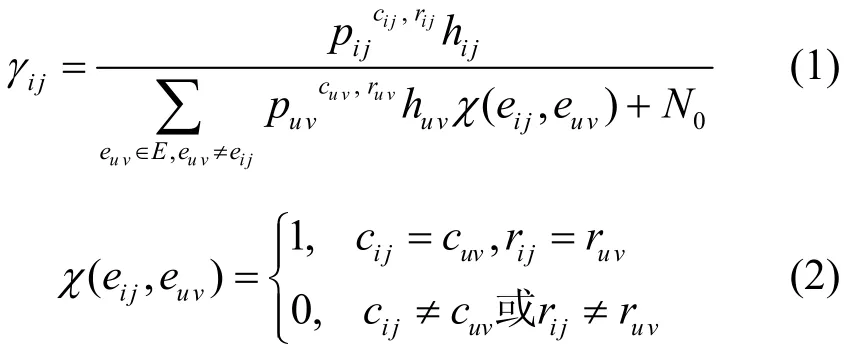
根据香农容量公式，本文给出的链路容量计算式如式(3)所示，若链路eij在信道cij、时隙rij中的发射功率为pij，则链路eij的容量为

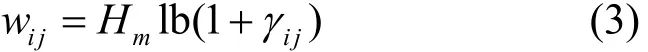
由式(3)可知，链路容量与信噪比的大小有关，信噪比越小，链路容量越小，进而网络容量越小。

3 资源分配多目标优化模型

无线传感器网络在实际应用中一般都会涉及多个目标的同时优化，这些性能指标之间往往是相互联系、相互制约的关系[15～17]。多目标优化问题一般可以转化为单目标优化问题，但是转化之后的单目标函数对权重的依赖性较大，权重设置稍有不当，就会对结果产生很大的影响。因此，为了避免设置权重，本文以链路的干扰和冲突为约束条件，以减小网络能耗、最大化网络容量、提高资源分配的均衡性为3个目标函数，构建了系统的资源分配多目标优化模型，如式(4)～式(8)所示。

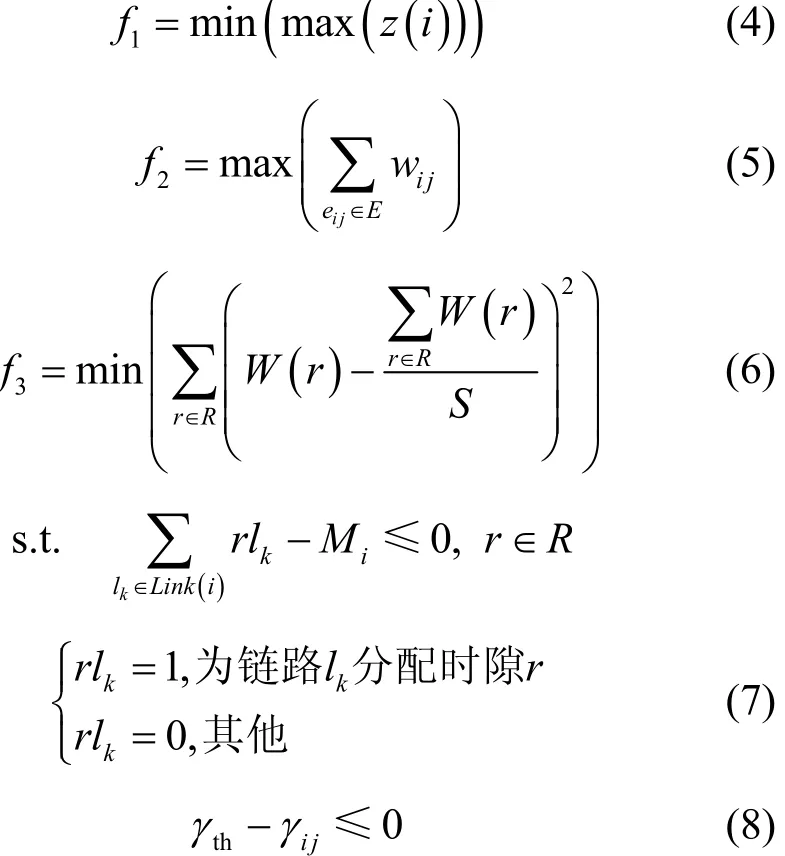
在上述模型中，式(4)表示最小化网络所有节点中最大的节点能耗，z(i)表示节点i在一个周期内的能耗，假设每个时隙的时间长度为t，时隙的个数为S，则节点在一个周期内的能耗可以表示为

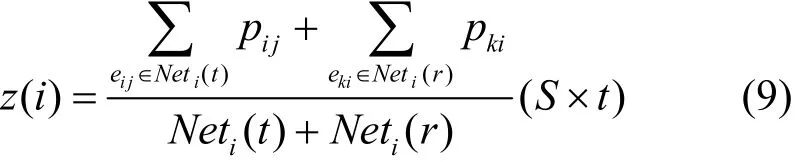
其中，Neti(t)表示以节点i为发射节点的链路集合，Neti(r)表示以节点i为接收节点的链路集合。

式(5)表示最大化网络容量。网络容量在一定程度上反映了通信质量的好坏，为保证目标函数的一致性，将式(5)转化为式(10)所示的最小化问题。

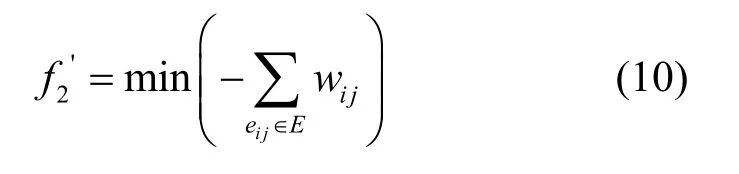
式(6)表示在各时隙内工作的所有链路的总容量的均衡性。若资源分配不均衡就会导致资源的浪费，甚至会出现网络拥塞的情况，造成网络通信时延。本文用各时隙内总容量的方差表示资源分配的均衡性。其中，W(r)表示处于第r个时隙的所有链路容量之和。

式(7)表示各节点的接口约束。由于各节点拥有的接口数量有限，且均小于正交信道的数量。有限的接口数量会使与节点关联的链路共享同一接口，而一个接口上的2条链路是不能在同一时间段内进行传输的。其中，Link(i)表示节点i的所有通信链路集合，Mi表示节点i的接口个数。

式(8)表示干扰约束。为了不影响正常通信，网络中的所有链路都应满足信噪比条件，即γij≥γth。

4 基于双群体差分进化的资源分配优化算法(RADEA)

双群体差分进化算法是一种用于解决多目标优化问题的简单高效的方法[18]。由于算法采用实数编码，因此，应用到无线传感器网络中可以有效地提高复杂网络系统的编码效率和运算速度。双群体差分进化算法迭代过程中分为2个种群的进化，一个是同时满足网络中所有节点的接口约束和干扰约束的占优可行解种群popf，反之，另一个是占优不可行解种群popc。popf还具有一定的记忆功能，lbest用于记忆popf中每一个个体搜索到的最优可行解，gbest用于记忆popf到目前为止搜索到的最优可行解，是外部存档集。算法的主要步骤包括个体编码及种群初始化、种群的变异和交叉、个体的选择与种群的更新。

4.1 个体编码及种群初始化

由于本文的资源分配是基于链路的，假设网络中的链路数量为L，则个体矩阵的维数为 3×L。任意一个个体的编码可以表示为

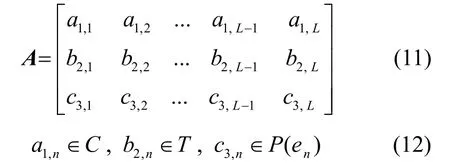
在进行种群初始化时，在信道、功率、时隙的可选范围内随机生成初始个体，每生成一个个体都要根据节点接口约束和链路干扰约束判断该个体的可行性，将可行解插入种群popf中，将不可行解插入种群popc中，一直循环，直到popf和popc都满足给定的种群规模N1、N2。

4.2 种群的变异和交叉

本文算法给出了2种变异策略，其中，策略1的目的在于通过向较优个体学习，改善算法的收敛速度。策略2的目的在于和不可行解进行信息交流，共享不可行个体的一些优良特性，增加资源分配方案群体的多样性。2种变异策略分别如式(13)和式(14)所示。

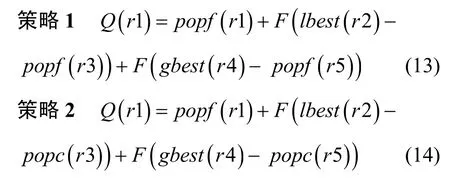
其中，Q(r1)是对应于popf中第r1个资源分配方案个体经过变异操作产生的实验个体，而其他为r2、r3、r4、r5的个体都是从对应集合中随机选择的有差异的个体。

算法中的交叉操作采用均匀的交叉方式，将资源分配方案个体矩阵的每列都作为一个交叉点，即每一条链路都是一个交叉点。如式(15)所示，Pj是针对实验个体Q(r1)中的第j列产生的位于区间[0,1]中的随机数，Cr是给定的参数。

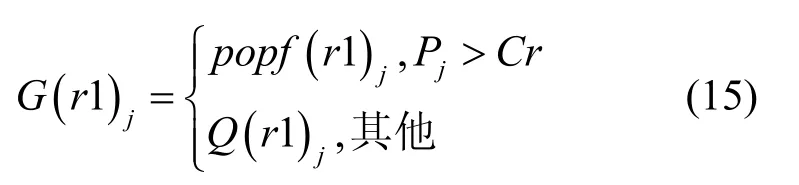
实验个体G(r1)的变量范围可能会超出本文规定的信道、功率及时隙的可选范围，这时需要对G(r1)中违反约束的元素进行边界条件处理[19]，并将处理后的个体记作son(r1)。

独立后的实验教学，利用实验室等实验条件并按照实验教学大纲的质量要求和学时要求全部实施完成，其开出率便可得以保证。

4.3 个体的选择与种群的更新

定义1 任意2个个体r1和r2，若r1和r2同时满足式(16)和式(17)，则称r1支配r2，记作r1 ≺r2。

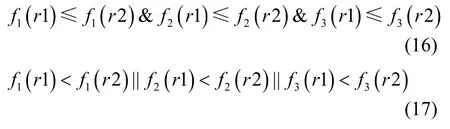
首先，判断子代种群son中个体的可行性，并将可行解和不可行解分别插入popf和popc中。然后，判断popf和popc中任意2个个体之间的支配关系，删除被支配个体，当种群规模达到N1、N2时停止判断。若删除所有被支配个体后种群规模依旧大于N1、N2，则计算个体的拥挤度[20]并将拥挤度小的个体删除以保证种群规模不会发生变化。

4.4 最佳均衡解

为了从pareto解集中选出一个最佳均衡解，本文为每个目标函数（fi）定义线性隶属度函数，如式(18)所示，其中，i= 1 ,2,3，将集合gbest中的每一个支配解（g）代入目标函数（fi）中，即可得到目标函数（fi）对应的最大值（）和最小值（）。

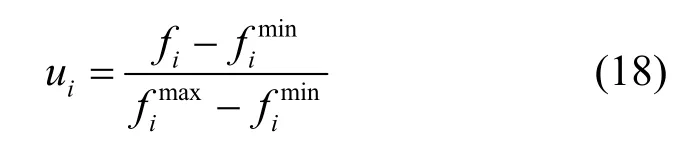
由式(18)可知，支配解个体对应的隶属度函数值越小表明目标函数实现的程度越强。对于gbest中的每一个支配解（g），定义聚合度函数如式(19)所示，聚合度函数表示支配解（g）对应的所有目标函数的隶属度之和，其中，m表示目标函数的个数，本文取m=3。

式(19)表明，聚合度函数值最小的个体就是本文要求的最佳均衡解。

4.5 算法步骤

综上所述，算法步骤概括如下。

Step1 为变异因子F、交叉概率Cr、迭代次数mmax、可行解种群规模N1和不可行解种群规模N2设初值。按4.1节所述产生初始种群popf、popc，并初始化lbest、gbest。

Step2popf中的个体经策略1或策略2的变异操作和式(15)所示的交叉操作后产生实验种群G。

Step3 对实验种群G中超出范围的元素进行边界条件处理产生子代种群son。

Step5 如4.3节所述更新popf和popc。

Step6 根据可行性与支配关系更新lbest。若son(r1)是可行解，则判断son(r1)是否支配于lbest(r1)，若son(r1)支配对应的个体lbest(r1)，则用son(r1)替换lbest(r1)，否则，不予替换；若son(r1)是不可行解，则lbest(r1)不更新。gbest属于外部存档集，按照 SPEA[21]中的方法更新gbest。m=m+1。

Step7 判断m≤mmax是否成立，若成立转Step2，否则，转Step8。

Step8 输出最优解集gbest。

Step9 根据线性隶属度函数和聚合度函数选出一个最佳均衡解。

5 仿真分析

本节在 Matlab环境下首先对算法中的参数进行仿真，然后通过对比实验对本文算法进行分析。

实验 1 为了选出合适的变异因子和交叉概率，首先对变异因子F和交叉概率Cr进行仿真实验。已知网络拓扑如图1所示，图1标号表示节点号，给定的网络节点数为25，链路数为24，其中箭头表示节点间通信的单向链路。在给定的拓扑图上，采用不同的变异因子和交叉概率组合运行本文算法，每组参数运行30次并取平均值，仿真结果如图 2所示。图 2(a)表示不同变异因子F和交叉概率Cr对各时隙负载均衡性的影响。图 2(b)和图 2(c)分别表示不同参数对节点能耗和网络容量的影响。实验1中其他参数设置如表1所示。

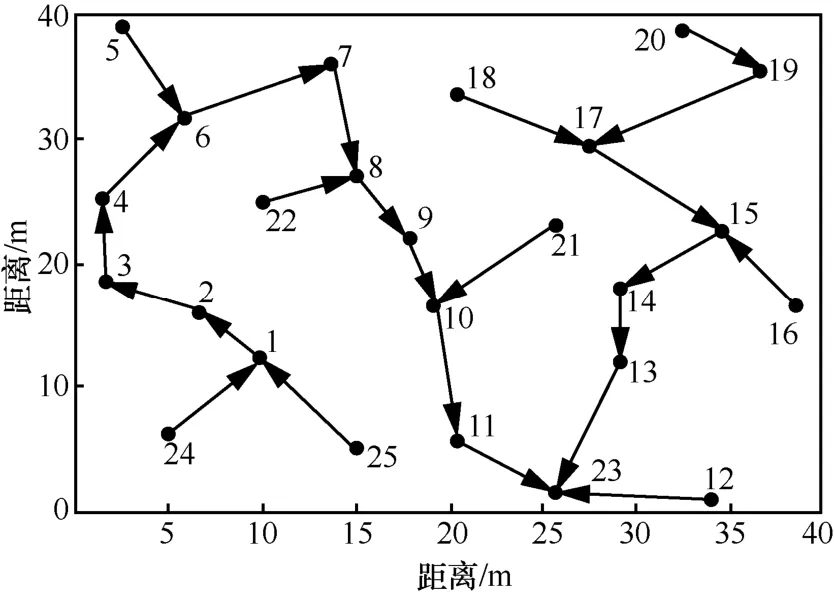
图1 网络拓扑

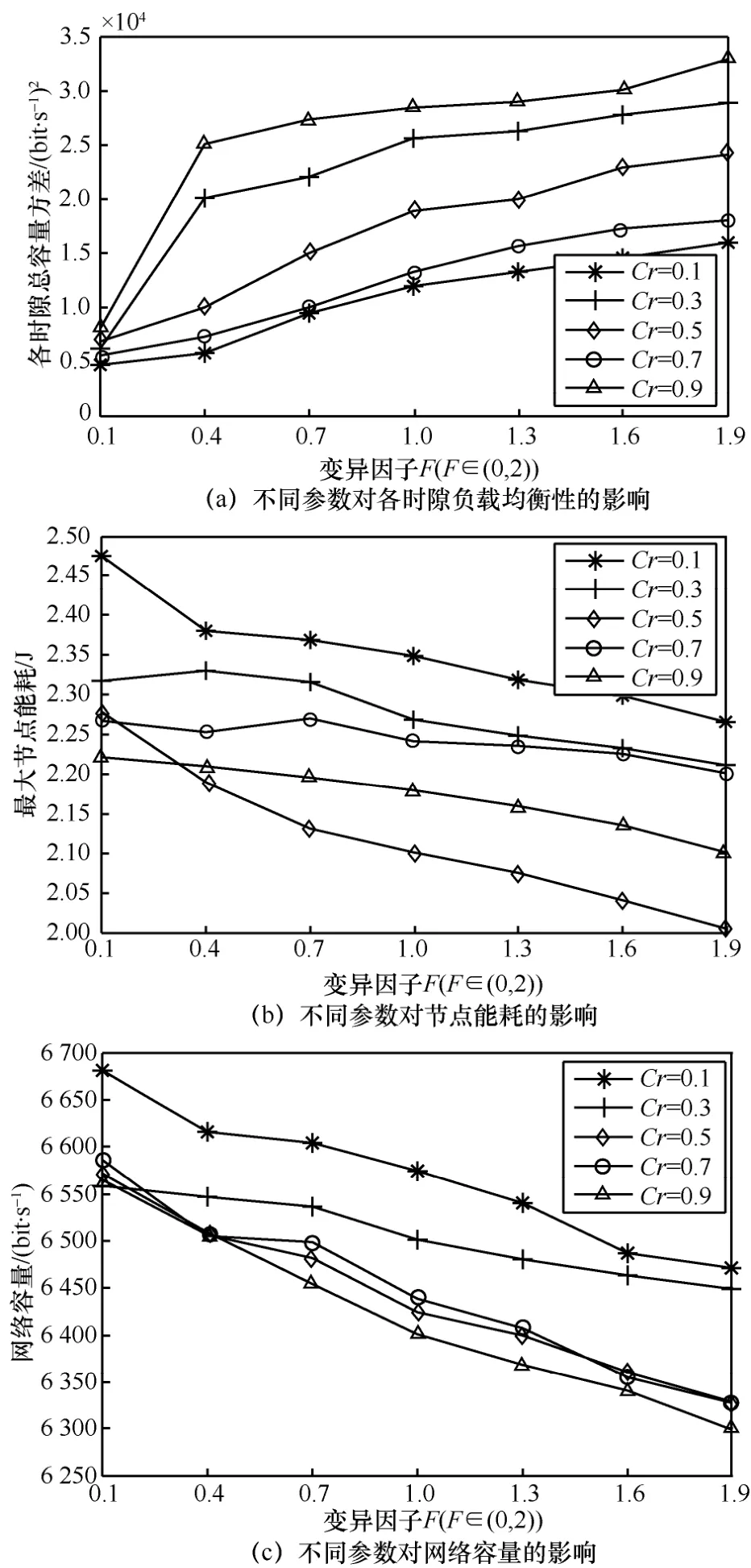
图2 不同参数对网络性能的影响

表1 仿真参数

通过对图2(a)的分析发现，当Cr=0.1、Cr=0.5和Cr=0.7时负载均衡性较好，但是由图2(b)可知，Cr=0.1时节点的能耗过大。此外，网络容量和负载均衡性都随F的增大而变差。综合考虑网络性能随F和Cr的变化，得到4组参数：F=0.1,Cr=0.5；F=0.1,Cr=0.7；F=0.4,Cr=0.5；F=0.4,Cr=0.7，如图 3 所示。由图3可知，F=0.1时算法收敛速度较快，并通过对F=0.1,Cr=0.5和F=0.1,Cr=0.7这2组参数对网络性能的分析可知，F=0.1,Cr=0.5时得到的各时隙负载均衡性和网络容量与F=0.1,Cr=0.7时得到的结果相差不大，但是由图 3(b)可知,F=0.1,Cr=0.7时的节点能耗远远大于F=0.1,Cr=0.5时的能耗。所以确定最终的参数为F=0.1,Cr=0.5。

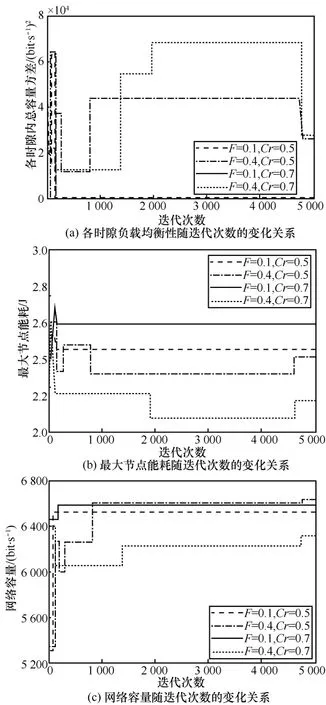
图3 不同参数对收敛速度的影响

实验 2 基于标准差分进化的资源分配优化算法[14]研究了功率控制与信道分配的联合分配问题，将文献[14]的算法和基于潜在博弈的功率控制和信道分配优化算法进行对比分析，仿真结果表明该算法在一定程度上降低了网络干扰，增大了网络容量。为了验证本文算法的性能，将本文算法与基于标准差分进化的资源分配算法进行对比，并将迭代次数设置为1 000次，其他实验参数与实验1相同，得到的信道分配和时隙分配结果如图4所示，各时隙内的负载均衡性如图 5所示。各链路干扰、各信道平均干扰和网络容量对比分别如图6～图8所示。

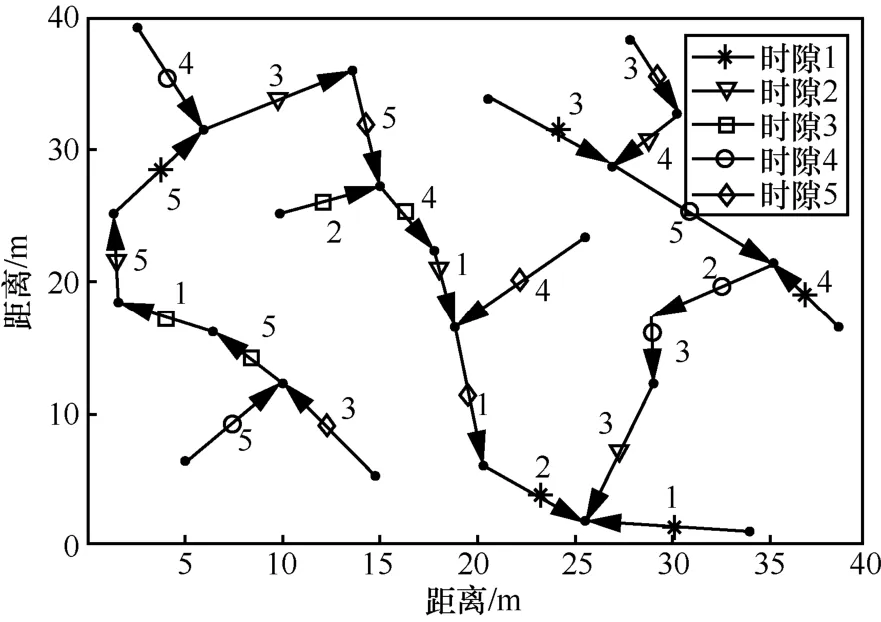
图4 信道分配和时隙分配结果

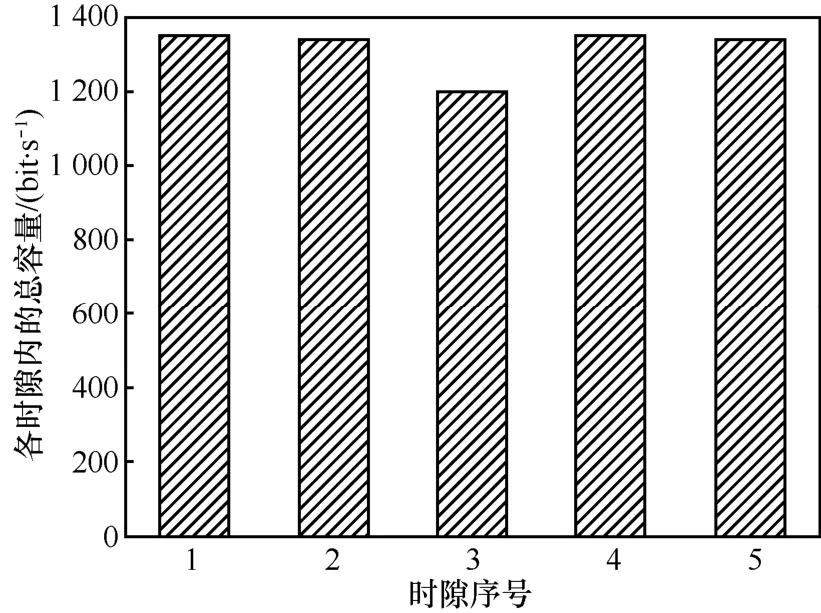
图5 各时隙负载均衡性

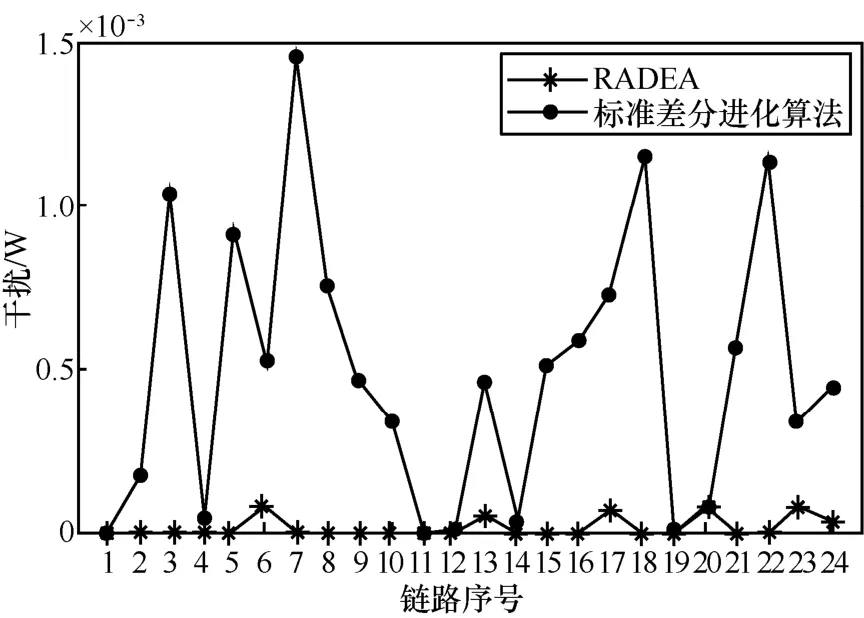
图6 各链路干扰

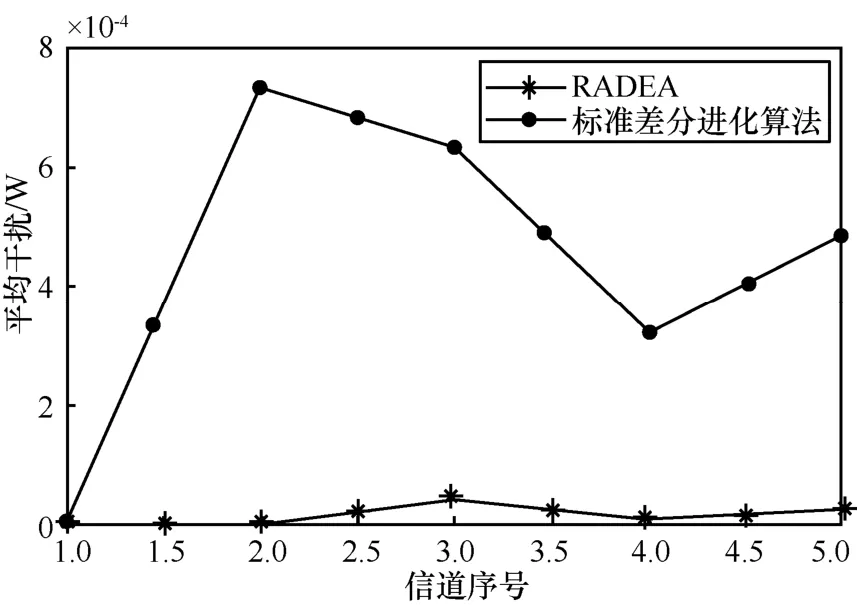
图7 各信道平均干扰

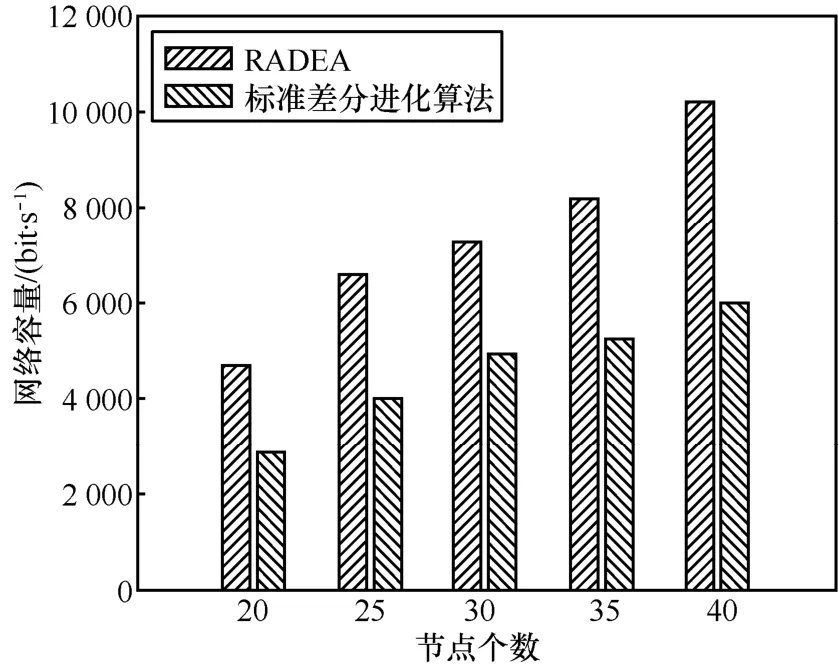
图8 网络容量对比

图 4和图 5分别表示本文算法运行的最终结果，图4中，处于不同时隙的链路用不同的符号标记，而链路上的数字表示该条链路通信所用的信道，由图4可以看出，得到的结果有效地避免了链路的通信冲突，最终整个网络所用时隙个数为 5个，且处于各时隙内的链路条数分别为5条、5条、4条、5条、5条，处于各信道内的链路条数分别为4条、3条、6条、5条、6条，结合图5，更能体现出资源分配的均衡性。

由图6可知，RADEA使各链路受到的干扰更加均衡，且接近于 0，由于标准差分进化算法并没有考虑时隙对干扰的影响，因此，使用标准差分进化算法得到的干扰大于 RADEA，且使用标准差分进化算法得到的干扰具有较强的波动性，同理，由图6中各信道内的平均干扰也可以看出，RADEA的抗干扰性更强。

由图7可知，由于RADEA得到的链路干扰要小于使用标准差分进化算法得到的链路干扰，所以，本文算法得到的网络容量远远大于使用标准差分进化算法的网络容量。

6 结束语

本文通过考虑时隙、信道和功率的交叉影响，首先建立了系统的资源分配多目标优化模型，然后在所建立的模型的基础上，提出了基于双群体差分进化的资源分配优化算法 RADEA，仿真结果表明RADEA能够有效地解决由于链路冲突和干扰过大而导致的能耗过大、容量受限和资源分配不均衡的问题。

参考文献：

[1]任丰源,黄海宁,林闯. 无线传感器网络[J]. 软件学报,2003,14(7):1282-1291.REN F Y,HUANG H N,LIN C. Wireless sensor network[J]. Journal of Software,2003,14(7):1282-1291.

[2]HAO X C,RU X Y,LI X D,et al. Energy efficient based channel assignment game algorithm for wireless sensor network[J]. Wireless Personal Communications,2014,85(4):2749-2771.

[3]SINEM C E,PRAVIN V. TDMA scheduling algorithms for wireless sensor networks[J]. Wireless Network,2010,16(4):985-997.

[4]XU X H,LI X Y,SONG M. Efficient aggregation scheduling in multi-hop wireless sensor networks with SINR constraints[J]. IEEE Transactions on Mobile Computing,2013,12(12):2518-2527.

[5]SHASHIDHAR G,MILIND D,RAVI P. Link scheduling in wireless sensor networks: distributed edge coloring revisited[J]. Journal of Parallel and Distributed Computing,2013,68(8):1122-1134.

[6]AL-ZAHRANI A Y,YU F R. An energy-efficient resource allocation and interference management scheme in green heterogeneous networks using game theory[J]. IEEE Transactions on Vehicular Technology,2016,65(7):5384-5396.

[7]张治学,曾波,张各各.基于多信道的能量高效传感器节点调度算法[J]. 计算机工程,2015,41(9): 135-139.ZHANG Z X,ZENG B,ZHANG G G. Energy efficient sensor node scheduling algorithm based on multiple channels[J]. Computer Engineering,2015,41(9):135-139.

[8]ABUSAYEED S,XU Y,LU C Y,et al. Distributed channel allocation protocols for wireless sensor networks[J]. IEEE Transactions on Parallel and Distributed Systems,2014,25(9):2264-2274.

[9]SONG Y,ZHANG C,FANG Y G. Joint channel and power allocation in wireless mesh networks: a game theoretical perspective[J]. IEEE Journal on Selected Areas in Communications,2015,26(7):1149-1159.

[10]HAO X C,GONG Q Q,HOU S,et al. Joint channel allocation and power control optimal algorithm based on non-cooperative game in wireless sensor networks[J]. Wireless Personal Communications,2014,78(2):1047-1061.

[11]HAO X C,RU,X Y,LI X D,et al. Joint game algorithm of power control and channel allocation considering channel interval and relay transmission obstacle for WSN[J]. Wireless Personal Communications,2015,86(2):521-548.

[12]郝晓辰,巩倩倩,侯爽,等.无线传感器网络中支持并行传输的信道与功率联合优化博弈算法[J]. 电子与信息学报,2014,36(7):1720-1727.HAO X C,GONG Q Q,HOU S,et al. Joint channel and power optimal game-theoretic algorithm for concurrent transmission in wireless sensor network. Journal of electronics & information technology[J].Journal of Electronics and Information Technology,2014,36(7):1720-1727.

[13]贾杰,李燕燕,陈剑. 认知无线网状网中基于差分演化的功率控制与信道分配[J].电子学报,2013,41(1): 62-67.JIA J,LI Y Y,CHEN J. Channel allocation and power control based on differential evolution algorithm in cognitive radio mesh network[J].Acta Electronica Sinica,2013,41(1):62-67.

[14]MERLIN S,VAIDYA N,ZORZI M. Resource allocation in multi-radio multi-channel multi-hop wireless networks[C]//27th IEEE Conference on Computer Communications (INFOCOM 2008). 2008:1283-1292.

[15]BAGHAEE H R.,MIRSALIM M,GHAREHPETIAN G B,et al.Security /cost-based optimal allocation of multi-type FACTS devices using multi-objective particle swarm optimization[J]. Simulation-Transactions of the Society for Modeling and Simulation International,2012,88(8):999-1010.

[16]WANG L F,SINGH C. Environmental / economic power dispatch using a fuzzified multi-objective particle swarm optimization algorithm[J]. The Electric Power Systems Research,2007,77(12):1654-1664.

[17]BAGHAEE H R,MIRSALIM M,GHAREHPETIAN G B. Reliability/cost-based multi-objective pareto optimal design of stand-alone wind/PV/FC generation microgrid system[J]. Energy,2016,115(15):1022-1041.

[18]孟红云,张小华,刘三阳. 用于约束多目标优化问题的双群体差分进化算法[J].计算机学报,2008,31(2):228-235.MENG H Y,ZHANG X H,LIU S Y. A differential evolution based on double populations for constrained multi-objective optimization problem[J]. Chinese Journal of Computers,2008,31(2):228-235.

[19] 周辉仁,唐万生,王海龙. 基于差分进化算法的多旅行商问题优化[J]. 系统工程理论与实践,2010,30(8):1471-1476.ZHOU H R,TANG W S,WANG H L. Optimization of multiple traveling salesman problem based on differential evolution algorithm[J].System Engineering Theory & Practice,2010,30(8):1471-1476.

[20]DEB K,PARTAP A,AGARWAL S,et al. A fast and elitist multiobjective genetic algorithm: NSGA-II[J]. IEEE Transactions on Evolutionary Computation,2002,6(2):182-197.

[21]ZITZLER E,THIELE L. Multiobjective evolutionary algorithms: a comparative case study and the strength pareto approach[J]. IEEE Transaction on Evolutionary Computation,1999,3(4):257-271.