循环载荷作用下加筋板格极限强度的理论解

，， ， ，

(1.浙江工业大学 建筑工程学院，浙江 杭州 310023；2.中国船舶与海洋工程设计研究院，上海 200011)

船舶结构的极限强度一直以来都是人们所关注的重要课题[1-3]，不少学者指出船舶结构的破坏不仅仅一次性过载破坏这一种，更多的还是由于循环载荷作用所导致的破坏[4-5].而加筋板格作为船舶结构的基本受力单元，其极限强度直接影响船舶结构的总体极限强度，所以，对循环载荷作用下加筋板格极限强度的研究具有十分重要的意义.

1985年，Fukumoto等[6]基于大挠度小应变理论对矩形板在循环面内载荷以及横向载荷作用下的变形性能进行了研究，并且绘制出了矩形板的循环加载曲线.1998年，Usami等[7]运用非线性有限元方法研究了加筋板格及钢制板等结构在循环载荷作用下的循环特性，得到了计算相应结构强度和刚度的理论公式.在国内，黄震球等[8-9]基于刚塑性理论与弹性大变形理论，推出了循环面内载荷作用下方形板和矩形板的非弹性大挠度变形特性.同时通过对方柱进行循环加载试验，获得了循环载荷作用下方板的载荷—变形曲线.通过对比发现，试验结果与理论解相差很小.刘恪畅等[10-11]采用基于两端简支梁-柱模型的Rahman法，推出了加筋板格在循环载荷作用下的应力应变关系式.但由HCSR规范可知，对于连续加强筋的加筋板格，理论计算模型的边界条件取为两端固支更符合实际边界[12]，故基于两端固支的梁-柱模型，推导了循环载荷作用下加筋板格极限强度和应力应力关系的理论计算公式.并运用非线性有限元进行了实例计算.结果表明：相比于采用两端简支边界的Rahman法，采用两端固支边界的理论方法其计算结果与有限元的结果更为接近.

1 理论方法

1.1 理论计算模型

理论计算模型范围为：横向在纵骨两边各取半个带板宽度，纵向取两相邻横梁间的一跨距离，跨度设为a.将作用在加筋板格翼缘上的均布载荷简化为线载荷q作用于弯曲平面内，并在模型两端沿轴线作用轴力N，如图1所示.此外，以下所有计算均不考虑剪力的影响，因其影响小，可忽略不计.

图1 两端固支计算模型Fig.1 Two end fixed calculation model

1.2 受压加筋板格的极限强度

对于只有轴向载荷作用，以及轴向载荷和较小或中等侧向载荷组合作用下加筋板格的受压失效，加筋板板格主要发生加强筋面板受压失效和带板受压失效2种失效模式.

1983年，Hughes给出了计算以上2种失效模式对应的加筋板格极限强度σult的理论方法.但Hughes的方法是基于两端简支假设的.

对于两端固支计算模型，将梁柱在反弯点处分成3段，原来两端固支的梁柱就被分为3段两端相当于简支的梁柱，然后对各段按照Hughes的方法求极限强度.假设加筋板格跨中截面达到极限强度时为极限状态，故只需对中间段求其极限强度.下面结合图1的计算模型，分别对2种失效模式求其极限强度.

如果发生的是加强筋面板受压失效，则加筋板格的受压极限强度计算式为

(1)

式中：I，A分别为横截面的惯性矩和面积；yf为面板的厚度中心至截面中和轴的距离；M0，δ0分别为仅有侧压作用时的最大弯矩和最大挠度；Δ为梁柱的初始偏心；Φ为轴向应力引起的放大因子；σF为加强筋面板厚度中心的应力；σuf为加强筋面板受压失效时轴力引起的截面平均应力.

如果发生的是带板受压失效，则加筋板格的受压极限强度计算式为

(2)

式中：Ie，Ae分别为有效截面的惯性矩和面积；yp为带板的厚度中心至截面中和轴的距离；Δp为因带板的刚度损失而导致的截面偏心距；σF为带板厚度中心的应力；σue为带板受压失效时轴力引起的截面平均应力；其他变量同式(1).

式(1，2)中的系数γ和ν的取值方法：当侧向载荷为0时，γ=0，ν=0.5；当侧向载荷不为0时，通过计算仅有侧向载荷作用时反弯点的位置和各点挠度的比例关系可得γ=0.556，ν=0.577；若侧向载荷为0，极限强度σult取式(1，2)中σuf和σue两者的较小值.

1.3 受压加筋板格的应力应变关系

参照Rahman等[3]的方法将加筋板格受压时的应力应变关系分为3个区段：依次为稳定区、非卸载区和卸载区，如图2所示.各区段的应力应变关系表达式参照Rahman法.

图2 受压加筋板格平均应力应变曲线Fig.2 Average stress-strain curve of compressed stiffened panel

1.4 受压加筋板格的卸载

参照刘恪畅等[10-11]的方法，假设在任何阶段的卸载都为弹性卸载，故卸载的平均应力应变关系容易求得，且对于卸载后的残余挠度'和残余应变ε′，其计算方法如下：

假设加筋板格经历了一次轴向压缩载荷的循环作用，载荷的历程为

σx∶0→σ→0，εx∶0→ε→0

卸载完成后，恢复的挠度δw和应变δε计算式分别为

(3)

设卸载后加筋板格的残余挠度和残余应变分别为Δ′和ε′，则有

w-δw=Δ′+δ0，ε′=ε-δε

(4)

式中：w，ε分别为卸载点对应的挠度和应变，由式(4)便可求得在各区段卸载时对应的残余挠度Δ′和残余应变ε′.下面分别给出在各个区段卸载时，残余挠度Δ′和残余应变ε′的计算公式.以下公式中考虑了加筋板格的初始挠度，并假设其初始应变为0.

1.4.1 稳定区卸载

对于面板受压失效的加筋板格，即

Δ′=Δ，ε′=0

(5)

对于带板受压失效的加筋板格，即

Δ′=Δ

(6)

式中：εult为极限应变；T为割线模量；b，tp分别为带板的宽度和厚度.

1.4.2 非卸载区卸载

对于面板受压失效的加筋板格，即

(7)

对于带板受压失效的加筋板格，即

(8)

1.4.3 卸载区卸载

对于面板受压失效的加筋板格，即

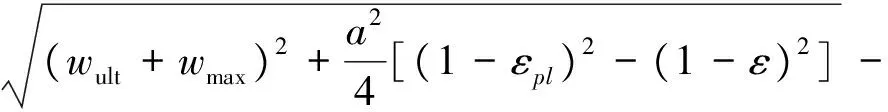
(9)

对于带板受压失效的加筋板格，即

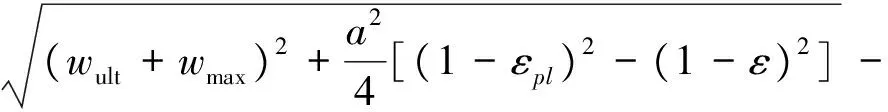
(10)

式中：wult为两种失效模式下应力刚达到极限值时加筋板格跨中处的挠度；wmax为加筋板格在非卸载区内跨中处最大挠度的增量值.

1.5 循环加载的计算流程

循环载荷作用下加筋板格极限强度的计算流程如下：

1)计算加筋板格的受压极限强度σult.

2)给定加筋板格的卸载应变εu，同时判断卸载发生在哪个区段.

3)根据相应区段的公式算得卸载完成后加筋板格的残余挠度Δ′和残余应变ε′.

4)将上一次循环卸载后得到的残余挠度Δ′和残余应变ε′作为初始条件，计算下一次循环加载时加筋板格的极限强度.

5)重复步骤1)～4)，便可得到加筋板格在轴向循环载荷作用下的极限强度以及平均应力应变关系曲线.

需要注意的是，随着载荷不断增大及塑性铰的形成，加筋板格的边界条件也在改变，为了更合理地反应实际情况，可以做如下假设：如果在某次循环时，应变超过了塑性铰应变εpl，即跨中已经形成塑性铰，此时两端也已形成塑性铰，则下一次加载时加筋板格的极限强度取跨度为a的两端简支模型计算.但跨中的弯矩和挠度仍取M0=qa2/24，δ0=qa4/384EI.

2 数值分析

2.1 有限元模型

参照ISSC[13]的方法，有限元模型范围取：纵骨两边各取半个带板宽度，横梁两边各取半跨长度.单元类型为4结点板壳单元，网格尺寸带板为50 mm×50 mm，加强筋腹板为50 mm×50 mm，加强筋面板为50 mm×45 mm，如图3所示.采用考虑应变硬化影响的双线性本构模型和Von-Mises屈服准则，非线性迭代方法采用弧长法[14-16].

B1，B2，B3，B4—周边约束；C1，C2，C3，C4—角点约束；FR1—横梁约束图3 有限元模型Fig.3 Finite element model

2.2 边界条件

若以X，Y，Z代表平动约束，RX，RY，RZ代表转动约束，则图3中各边界条件如表1所示.

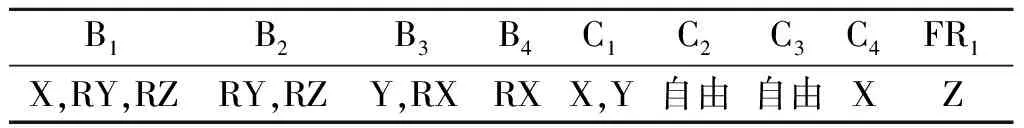
表1 边界条件Table1 Boundary condition

2.3 几何初始缺陷

模型所加的几何初始缺陷包括整体缺陷和局部缺陷，参照ISSC考虑.

2.4 残余应力

由于理论方法中考虑了10%(即σr/σy=0.1)的残余应力，所以有限元模型也考虑10%的残余应力，为简化分析，仅考虑带板的残余应力，其分布如图4所示(正为拉应力，负为压应力).

图4 残余应力的分布Fig.4 The distribution of residual stress

由残余拉、压应力自相平衡可得

(11)

2.5 实例计算与结果对比

2.5.1 算例尺寸

采用的算例尺寸跨度a=2 400 mm，带板宽bp=800 mm，带板厚tp=19 mm，腹板高hw=250 mm；腹板厚tw=12 mm，翼缘宽bf=90 mm，翼缘厚tf=16 mm.采用的材料为钢材，屈服强度为235 MPa，泊松比ν=0.3.

2.5.2 计算结果对比

考虑加筋板格的单向循环加载，其加载路径为0—1.4εy—0—2.1εy—0—3.2εy—0—3.5εy，εy为材料的屈服应变.现将采用理论方法计算得到的结果与有限元分析得到的结果进行对比，汇总如下：

1) 无侧向载荷作用的单向循环加载

对于无侧向载荷作用的情况，每次循环的极限强度汇总见表2和图5，平均应力应变曲线如图6所示.

表2无侧向载荷作用每次循环极限强度汇总

Table2Summaryoftheultimatestrengthofeachcyclewithoutlateralload

极限强度循环数n/次1234有限元法极限强度0．8690．8130．6230．510两端简支极限强度0．8150．6670．5490．481误差/%-6．2-18．0-11．9-5．7两端固支极限强度0．8230．7440．5690．490误差/%-5．3-8．5-8．7-3．9

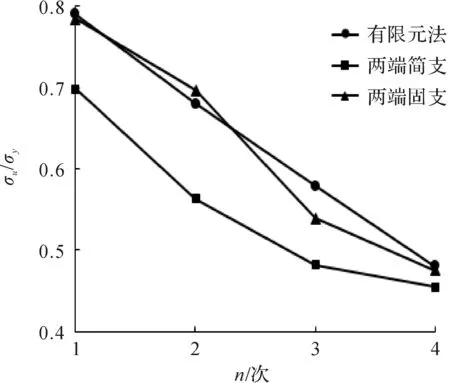
图5 无侧向载荷作用每次循环的极限强度Fig.5 The ultimate strength of each cycle

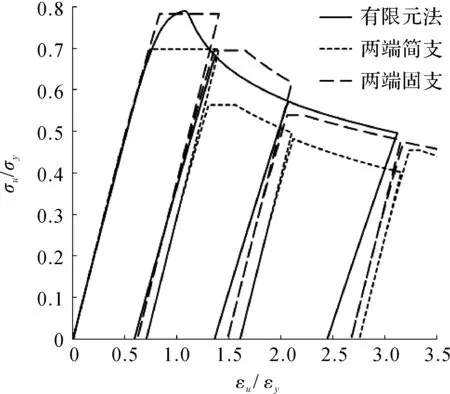
图6 无侧向载荷作用平均应力应变曲线Fig.6 The average stress-strain curve

由表2，图5，6可以看出：当无侧向载荷作用时，相比于两端简支模型，两端固支模型算得的加筋板格每次循环的极限强度与有限元方法的结果更为接近，最大误差为-8.7%，而两端简支模型算得的误差最大达到-18%.

2) 有侧向载荷作用的单向循环加载

对于有侧向载荷(0.16 MPa)作用的情况，每次循环的极限强度汇总见表3和图7，平均应力应变曲线如图8所示.

表3有侧向载荷作用每次循环极限强度汇总

Table3Summaryoftheultimatestrengthofeachcyclewithlateralload

极限强度循环数n/次1234有限元法极限强度0．7900．6800．5790．480两端简支极限强度0．6980．5630．4820．455误差/%-11．6-17．2-16．8-5．2两端固支极限强度0．7840．6960．5390．475误差/%-0．82．4-6．9-1．0

图7 有侧向载荷作用每次循环的极限强度Fig.7 The ultimate strength of each cycle

图8 有侧向载荷作用平均应力应变曲线Fig.8 The average stress-strain curve

由表3，图7，8可以看出：当有侧向载荷作用时，相比于两端简支模型，两端固支模型算得的加筋板格每次循环的极限强度与有限元方法的结果更为接近，最大误差为-6.9%，而两端简支模型算得的误差最大达到-17.2%.

3 结 论

通过比较理论方法和数值分析的结果，基于两端固支的梁-柱理论模型来计算加筋板格在轴向循环载荷作用下的极限强度是比较合理的，无论是有限元方法，还是理论方法，计算结果都表明：加筋板格的塑性变形随着循环次数的增加而在逐渐累积，其极限强度也因此而不断下降；相比基于两端简支假定的Rahman法的计算结果，基于两端固支假定的理论方法与有限元方法的计算结果更加接近，说明对两端采用固支边界更符合实际情况.

参考文献：

[1] CALDWELLJ B. Ultimate longitudinal strength[J]. Transportation RINA，1965，107:417-430.

[2] SMITHC S. Influence of local compressive failure on ultimatelongitudinal strength of a ship’s hull[J]. PRADS symposium，1977，15：73-79.

[3] RAHMAN M K, CHOWDHURY M.Estimation of ultimate longitudinal bending moment ofships and box girders[J]. Journal of ship research，1995，40(3):244-257.

[4] 黄震球.关于海船船体总强度准则的一个新见解[J].武汉造船，1993(6)：8-12.

[5] 黄震球，陈齐树，骆子夜.循环弯曲载荷下船体梁的极限纵强度[J].中国造船，1996(3)：87-95.

[6] FUKUMTO Y, KUSAMA H. Cyclic behavior of plates under in-plane loading[J]. Engineering structures，1985，7:56-63.

[7] USAMI T, GE H B. Cyclic behavior of thin-walled steel structures-numerical analysis[J]. Thin-walled structures，1998.

[8] 黄震球.循环压缩-拉伸荷载下矩形板的极限强度[J].华中理工大学学报，1994(4)：36-41.

[9] 黄震球，陈齐树，骆子夜，等.循环面内压缩载荷下方板的非弹性变形性能[J].华中理工大学学报，1996(3)：39-42.

[10] 刘恪畅.循环弯曲下船体梁极限强度研究[D].武汉：武汉理工大学，2012.

[11] 喻霁.循环弯矩作用下的船体梁逐步崩溃行为的研究[D].武汉：武汉理工大学，2013.

[12] IACS. Common structural rules for bulk carriers and oil tankers: BS 0101—2014[S]. London: International Association of Classification Societies，2014.

[13] KIM B, JERZY C, JOSE M G, et al. Committee III.1-ultimate strength[C]//PAIK J K. Proceedings of the 17th international ship and offshore structures congress (ISSC). Seoul， Korea: ISSC Committee，2009:375-474.

[14] 蒲军平，姚宇龙.平面有限元网格实用划分方法研究[J].浙江工业大学学报，2012，40(1)：88-91.

[15] 袁伟斌，徐洁，叶呈敏.纯弯下简支角钢梁静态和动态不稳定性分析[J].浙江工业大学学报，2013，41(6):677-681.

[16] 崔钦淑，蒋金杰.基于ABAQUS的RCZ形柱框架顶层节点抗震性能分析[J].浙江工业大学学报，2016，44(3):310-315.