修正Durrmeyer型Bernstein-Stancu算子的逼近

徐华，钱程

(1. 杭州师范大学钱江学院， 浙江 杭州 310036； 2. 杭州师范大学 理学院， 浙江 杭州 311121)

0 引 言

以C[0,1]表示定义在闭区间[0,1]上连续函数的全体，对于任意f∈C[0,1]的函数，其对应的Bernstein算子和Bernstein-Durrmeyer算子分别定义如下：

其中，

这2类算子在逼近论和计算数学等领域有许多重要的应用，对其逼近性质的研究也已经相当广泛. 2010年，GADJIEV等[1]定义了以下推广形式的Bernstein-Durrmeyer型算子：

其中，αk,βk,k=1,2为满足以下条件的正常数： 0≤α1≤β1,0≤α2≤β2,而

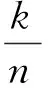
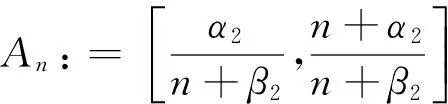
最近，DONG等[4]引入了下列基于Sn,α,β(f,x)的Durrmeyer型算子：

其中，

由于(lemma 1[3])

(1)

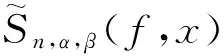
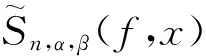
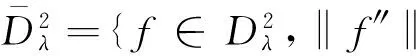
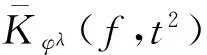
t4/(2-λ)‖g″‖},

(2)

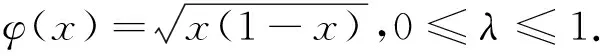
(3)

其中x～y意为存在正常数c使得c-1y≤x≤cy.

本文的主要结论为：

定理1设f为[0,1]区间上的连续函数，0≤λ≤1. 则存在一个仅依赖于λ,α1,α2,β1,β2的正常数C，使得

其中，

而ω(f,t)为f在[0,1]上的通常连续模.

文中，C总表示一个绝对正常数或仅依赖于某些参数(除f,n和x以外)的正常数，其值在不同地方可以不同.

定理2设f为[0,1]区间上的连续函数，0<α<2/(2-λ),0≤λ≤1,则

意味着

(ii)ω(f,t)=O(tα(1-λ/2)).

1 引理及证明

引理1对于任意γ≥0，有

x∈[0,1].

证明利用文献[3]中的引理1，对任意γ≥0，有

因此，

由此，引理1得证.

引理2对任意x∈[0,1]，有

证明记

由文献[6]有

且有

(5)

注意到(见文献[4])：

Δn(x)～δn(x),x∈[0,1].

(6)

由式(5)即得

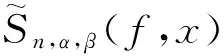
引理2得证.

引理3对任意x∈[0,1]，有

(7)

(8)

证明直接计算，得

又因为

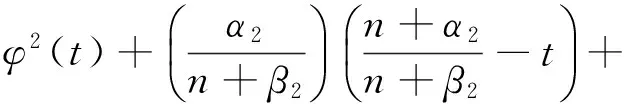
第2阶段，继续推进“四同步”工作机制，以副中心道路新建、改建和扩建为契机，全面推进城市副中心新城155 km2智慧交通管理科技系统建设.

所以

由此，

(9)

若x∈[0,1]An，不妨设

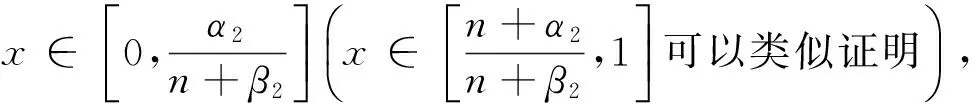
(10)

若x∈An，则有

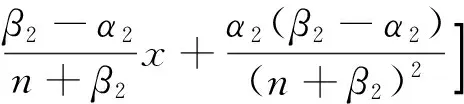
(11)

综合式(9)～(11)，即得式(9).

下证式(8).由式(6)知：

因此，

置

Cα,λ={f∈C([0,1]),‖f‖0<+};

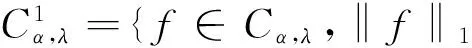
引理4如果0≤λ≤1,0<α<2,则

(12)

(13)

证明分2种情形证明式(12).

Δn(x)～φ(x),x∈Bn.

(14)

通过简单计算可得

(15)

其中，

(16)

由式(13)～(16)得

由引理1和引理3，得

情形2

此时，显然有

注意到

其中,qn-1,-1(x)=qn-1,n(x)=0,故有

利用式(16)并使用Hölder不等式2次，得到

上式第4个不等式利用了以下事实(由类似于式(7)的推导可得)：

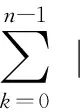
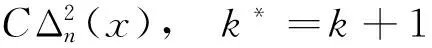
综合情形1和2的讨论，式(12)获证.

现在，证明式(13). 如果

则使用Hölder不等式2次，可得

C‖f‖1.

上式最后一个不等式用到了式(8).

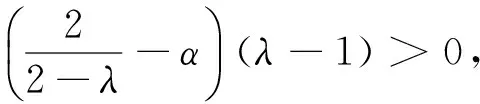
类似于引理4的证明，可以得到：

引理5若0≤λ≤1,0<α<2,那么

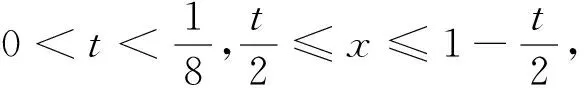
x∈[0,1],β<2,则有

x∈[0,1],0≤β≤2,则有

2 定理的证明

定理1的证明定义辅助算子

(17)

其中，

易知

(18)

Sn,α,β(1,x)=1,Sn,α,β(t-x,x)=0,

(19)

‖Sn,α,β‖≤3.

(20)

由式(18)可知，

(21)

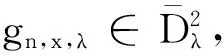
(22)

(23)

(24)

由式(20)和(21)有

|Sn,α,β(f,x)-f(x)|≤|Sn,α,β(f-g,x)|+

|f(x)-g(x)|+|Sn,α,β(g,x)-g(x)|≤

4‖f-g‖+|Sn,α,β(g,x)-g(x)|≤

(25)

注意到φ2λ(x)与Δ2λ(x)在[0,1]上是凹函数，对于任意的t,x∈[0,1],以及介于x与t之间的u，令

u=θx+(1-θ)t, 0≤θ≤1,

则有

(26)

(27)

利用Taylor公式:

以及式(19)与(27),有

当x∈Bn时，由式(14)、(26)、(18)、引理2和式(23)，得

Cn-1Δ2-2λ(x)‖φ2λg″‖≤

(28)

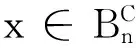
(29)

上式最后一个不等式利用了式(23)和(24).

结合式(17)、(21)、(25)、(28)与(29)，定理1得证.

定理2的证明由引理4～引理7，按照文献[7]中的方法可证得定理2，此证明略.

参考文献(References)：

[1] GADJIEV A D, GHORBANALIZACH A M. Approximation properties of a new type Bernstein-Stancu polynomials of one and two variables[J].AppliedMathematicsComputation, 2010, 216(3)： 890-901.

[2] STANCU D D. Approximation of functions by a new class of linear polynomial operators[J].RevueRoumainedeMathematiquesPuresetAppliquees, 1968, 13(8)： 1173-1194.

[3] WANG M L, YU D S,ZHOU P.On the approximation by operators of Bernstein-Stancu types[J].AppliedMathematicsComputation, 2014, 246(11)： 79-87.

[4] DONG L X, YU D S, ZHOU P. Pointwise approximation by a Durrmeyer variant of Bernstein-Stancu operators [J].JournalofInequalityApplications, 2017(1)： 28.Doi: 10.1186/S13660-016-1291-x.

[5] DITZIAN Z, TOTIK V.ModuliofSmoothness[M]. Berlin/New York： Springer-Verlag, 1987.

[6] ACAR T, ARAL A, GUPTA V. On approximation properties of a new type Bernstein-Durrmeyer operators[J].MatheticalSlovaca, 2015,65(5)： 1107-1122.

[7] GUO S, LIU L. The pointwise estimate for modified Bernstein operators[J].StudiaScientiarumMathematicarumHungarica, 2001, 37(1)： 69-81.