基于自适应和变游走方向的改进狼群算法
郭立婷
(西安电子科技大学 数学与统计学院, 陕西 西安 710126)
0 引 言
受自然界生物活动现象的启发,研究人员提出了多种智能优化计算方法.文献[1]模拟蚂蚁社会分工与协作觅食的行为,提出了蚁群算法(ant colony optimization,ACO);文献[2]模拟鱼群捕食中的觅食、聚群等行为提出了鱼群算法(fish swarm algorithm,FSA);文献[3]模拟萤火虫发光吸引同伴现象,提出萤火虫优化算法(glowworm swarm optimization,GSO). LIU等[4]模拟自然界狼群捕猎行为,提出了狼群算法(wolf colony algorithm,WCA);吴虎胜等[5]模拟狼群捕食行为及其猎物分配方式,抽象出狼群游走、召唤、围攻3种智能行为以及“胜者为王”的头狼产生规则和“强者生存”的狼群更新机制,提出狼群算法(wolf pack algorithm,WPA),并通过15个典型的复杂函数实验将WPA算法与FSA算法、PSO算法、GA算法进行了比较,WPA算法在处理多峰、高维复杂函数上有明显优势. 自适应在智能优化算法中应用广泛,文献[6-7]基于人工鱼群算法的寻优机理,提出了4种自适应人工鱼群算法,通过赋予人工鱼更多的智能,使人工鱼根据鱼群状态自动地调整视野和步长,简化了参数设定,提高了收敛速度和寻优精度. 欧阳喆等[8]针对基本萤火虫算法在求解多峰函数时精度不高和后期收敛较慢的问题,引入荧光因子以自适应调整萤火虫步长,提出一种自适应步长萤火虫优化算法.文献[9]提出了一种动态自适应的改进蚁群算法等. 目前,已有一些文献对狼群算法做了改进. 文献[10-12]针对基本狼群算法的不足,分别提出了基于改进狼群搜索策略的狼群算法、基于领导者策略的狼群搜索算法和自适应学习的狼群智能算法.
本文在WPA算法的基础上,对狼群的移动步长和方向进行改进. 对游走、召唤、围攻行为的移动步长提出了自适应步长方法,使得每只狼的移动步长可根据狼群状态动态变化,提高了搜索的精细程度,加快了收敛速度;通过改进游走行为的搜索方向,提高了搜索效率;通过全面覆盖搜索范围,对参加召唤行为的猛狼选取提出了新的策略. 综合以上策略提出了一种基于自适应和变游走方向的改进狼群算法(MACWPA).
1 基本狼群算法
基本狼群算法中,狼群按照职责分工,分为头狼、探狼和猛狼. 头狼为狼群首领,在每次迭代过程中提供基准信息;探狼负责搜寻食物,在游走行为中活动;猛狼负责向猎物方向奔袭,在奔袭行为中活动.假设在D维可行空间中初始化N只狼,头狼的位置定义为Xlead=(xlead1,xlead2,…,xleadD),目标函数值记为Ylead,其余狼位置定义为xi=(xi1,xi2,…,xiD),i=1,2,…,N-1,相应目标函数值记为Yi.
1.1 头狼产生规则
在迭代过程中,头狼位置是变化的,具有最优目标函数值的狼即为头狼. 头狼不执行3种智能行为而直接进入下次迭代,直到被其他目标值更优的狼替代.
1.2 游走行为
将解空间中除头狼外最佳的S_num只狼视为探狼. 若探狼i当前位置目标函数值Yi大于Ylead,则Ylead=Yi;若Yi小于Ylead,则探狼向h个方向分别前进一步(游走步长为stepa),并记录每前进一步后的目标函数值后退回原位置,探狼i按照式(1)向第p(p=1,2,…,h)个方向前进
(1)
探狼i选择的目标函数值最大且大于当前位置的方向前进一步,并更新之前状态xi. 重复以上游走行为直到探狼的目标函数值Yi大于Ylead或游走次数T达到最大值Tmax.
1.3 召唤行为
头狼召集周围M_num只猛狼以奔袭步长stepb迅速向头狼位置靠拢.则猛狼i根据式(2)更新当前位置
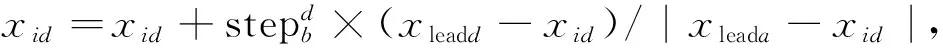
(2)
奔袭途中,若猛狼i感知到的目标函数值Yi大于Ylead,则Ylead=Yi,该猛狼转化为头狼并发起召唤行为;若Yi小于Ylead,则猛狼i继续奔袭直到其与头狼之间距离小于dnear:
(3)
式(3)中,ω表示距离判定因子.
1.4 围攻行为
猛狼联合探狼以攻击步长stepc对猎物G=(G1,G2,…,GD)进行围攻,以期将其捕获.狼群的围攻行为定义为
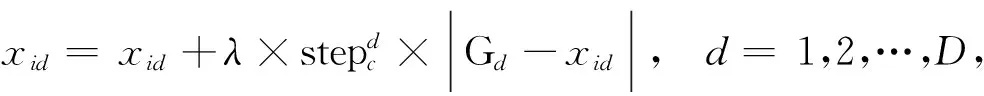
式(4)中λ为[-1,1]间均匀分布的随机数.
设待寻优第d个变量的取值范围为[mind,maxd],3种智能行为中所涉及的游走步长stepa、奔袭步长stepb、攻击步长stepc在第D维空间中存在以下关系:
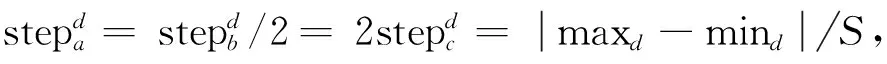
式(5)中,S表示步长因子,即狼在解空间中搜寻最优解的精细程度.
1.5 “强者生存”的狼群更新机制
除去目标函数值最差的R只狼,同时随机产生R只狼.R取[n/(2×β),n/β]间的随机整数,β为群体更新比例因子.
2 改进的自适应和变游走方向狼群算法
2.1 自适应法
吴虎胜等[5]提出的狼群算法中的移动步长分为3种,并按照式(5)定义. 但这种方式固化了步长,在算法初期会影响收敛速度,后期会降低搜索的精细程度,甚至可能错过最优值,仅获取最优值附近的较优值. 考虑到狼群算法中独有的特征: 头狼在每一步中都可能被目标函数值更好的狼替代,因此,采用自适应步长方法,狼i每一次移动的步长由该狼当前位置和当前头狼位置决定,离头狼位置越近的狼移动步长越小,以提高搜索的精细程度;离头狼越远的狼移动步长越大,以提高收敛速度,避免不必要的搜索.
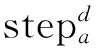
本文采用自适应步长:
step=rand×‖xi-Xlead‖2,
(6)
式(6)中rand表示[0,1]间的随机数. 自适应步长以头狼位置和狼当前位置为参考,当狼离头狼距离远时,以较大步长逼近头狼;当离头狼距离近时,以较小步长逼近头狼,加快收敛速度.
2.1.1 自适应游走行为
在游走行为中,按照游走次数的奇偶性,搜索方向在h和h+1两者之间变动(详见2.2).当游走次数为奇数次时,朝第p(p=1,2,…,h)个方向前进后,探狼i在第D维空间中所处的位置为
xid+sin(2π×p/h)×rand·norm(x(i,:)-Xlead);
(7)
当游走次数为偶数次时,朝第p(p=1,2,…,h,h+1)个方向前进后,探狼i在第D维空间中所处的位置为
xid+sin(2π×p/(h+1))×rand×norm(x(i,:)-Xlead).(8)
在游走行为中,不必担心某些狼因步长过长而错过全局最优解,游走行为中向h或h+1个方向试探的方法保证了搜索的全面覆盖.
2.1.2 自适应召唤行为
不同于基本WPA算法,在本文的改进算法中,参与召唤行为的猛狼不再只是头狼附近的狼,而是在除头狼外的全部狼群中随机选取M_num只狼作为猛狼. 经历长时间的游走行为后,头狼的位置发生多次更迭,如果只召唤头狼附近的狼向头狼逼近,会使算法陷入局部最优. 在除头狼外的狼群中随机选取猛狼,让他们只朝着头狼前进,使算法的搜索范围更广. 在奔袭过程中,当某只猛狼感知到其所在位置食物浓度更大时,会替代头狼,重新选取猛狼,进行召唤,直到其所在位置的食物浓度小于头狼位置的食物浓度. 同时,召唤行为也采取与游走行为相同的自适应步长法(6),则猛狼i根据式(9)更新当前位置:
xid=xid+step×(xleadd-xid)/|xleadd-xid|=
xid+rand×‖xi-xlead‖2×(xleadd-xid)/|xleadd-xid|,
d=1,2,…,D.
(9)
2.1.3 自适应围攻行为
猛狼联合探狼对猎物进行紧密围攻以期将其捕获,移动步长采用自适应步长法(6). 狼群围攻行为由式(10)表示:
d=1,2,…,D.
(10)
2.2 变游走方向法
在基本WPA算法中,虽然文献[5]提到每只探狼的猎物搜寻方式存在差异,h的取值是不同的,实际中可依据情况取[hmin,hmax]间的随机整数. 但是不论游走多少次,算法迭代多少次,对于探狼i来说,方向依然只有h个,而且在其试验中,参数h固定设置为10,而不是文献[5]所称的h是随机的. 从而导致搜索方向固定,搜索不精细.具体分析如下:
假如约定方向h为8个,一次移动后找到的最优方向如图1所示.
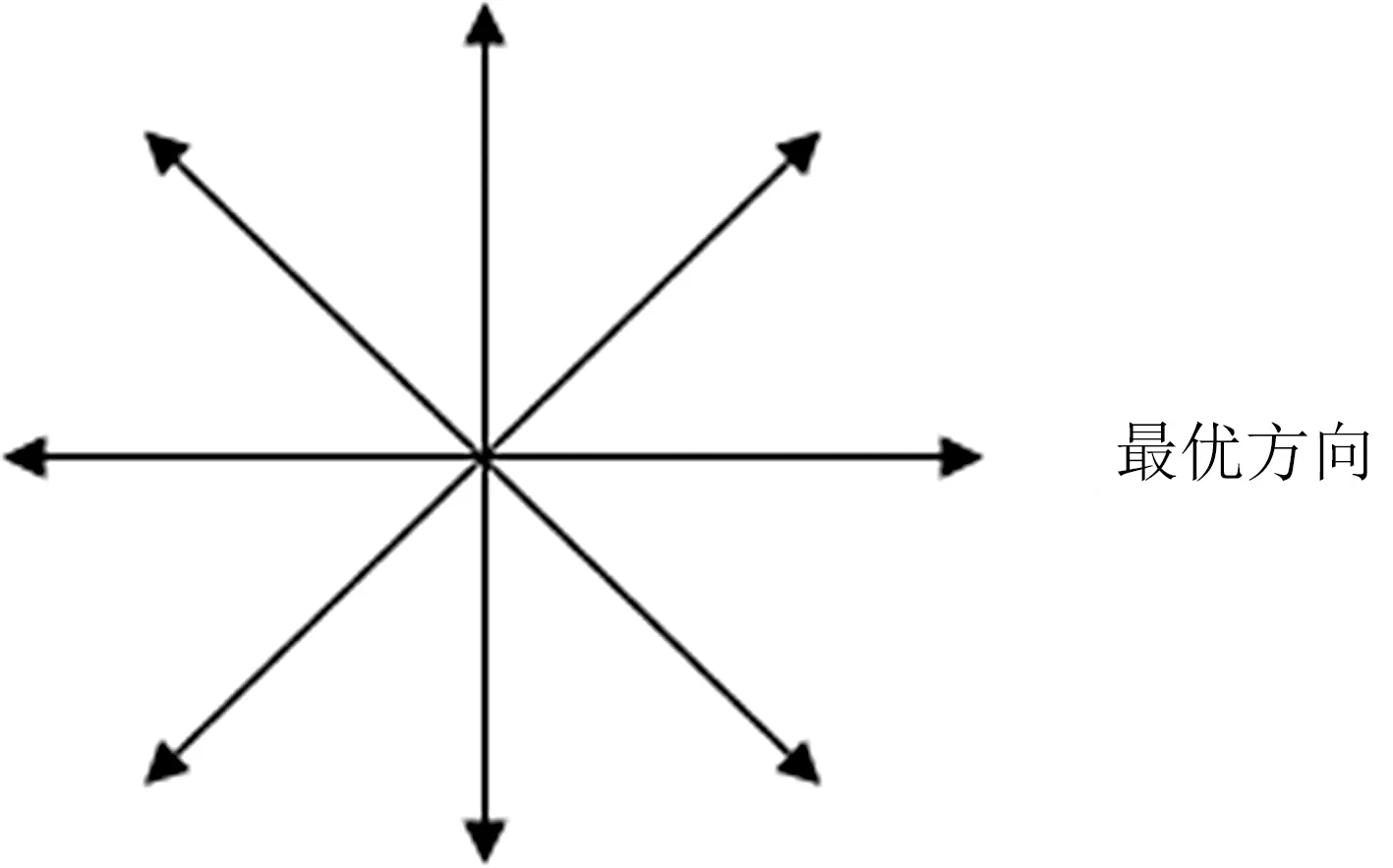
图1 WPA的游走方向Fig.1 Scouting direction of WPA
下次寻找最优方向时,每个方向都与该方向产生平行关系,并且之后都会沿着平行方向搜索,从而大大降低了搜索效率.
本文通过改进游走行为中h个方向的选取方法,根据游走次数T的奇偶性,搜索方向在h和h+1两者间变动,提高了搜索的精细度.效果图如图2所示.
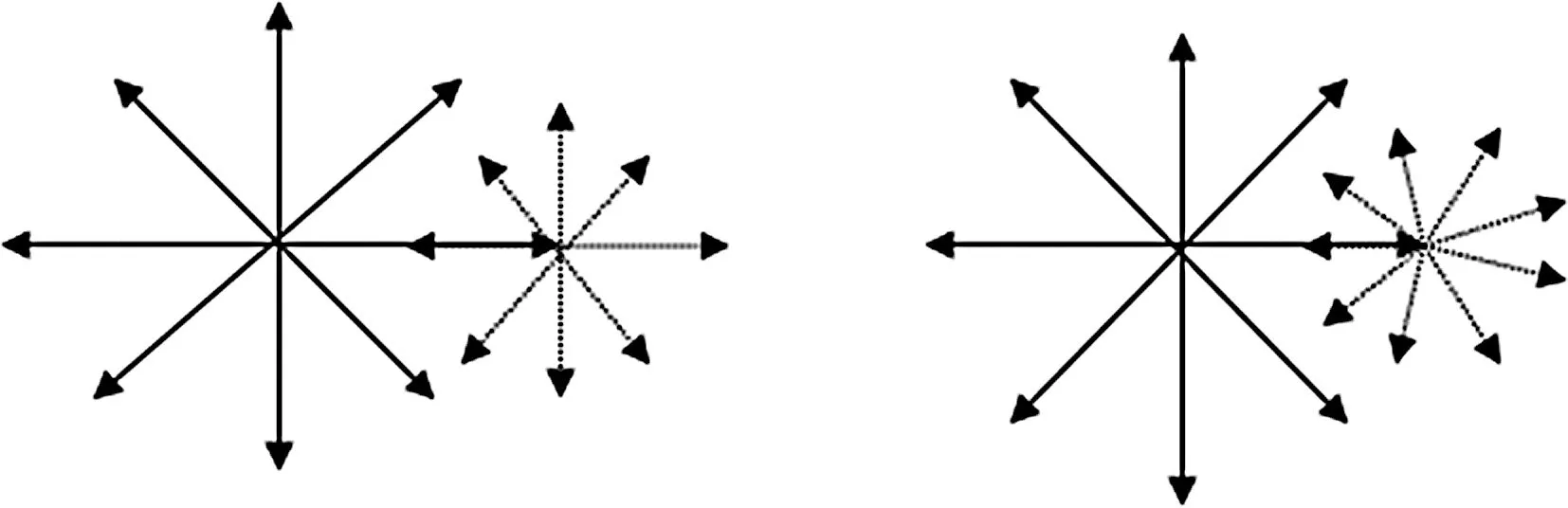
图2 变游走方向的MACWPA算法Fig.2 Changed scouting direction of MACWPA
从图2中可以看出,右边的第T次游走和第T+1次游走选取的方向不再成平行关系.结合文献[5]提出但未采用的每只探狼的搜索方向h在约定范围内随机选择的方法,丰富了搜索方向,进而扩大了搜索范围.
综上,根据最大游走次数交错变换方向数,方法简单、计算复杂度低,且不会对计算速度造成太大影响.
2.3 MACWPA算法描述
Step1数值初始化. 初始化狼群中狼位置Xi及其数目N,最大迭代次数Kmax,探狼比例因子α,最大游走次数Tmax,距离判定因子ω,更新比例因子β.
Step2选取目标函数值最好的狼为头狼,位置记为Xlead,目标函数值记为Ylead,除头狼外最佳的S_num只狼视为探狼,并按照公式(7)、(8)执行游走行为,直到每只探狼游走次数达到最大游走次数Tmax,转step3.
Step3从除头狼外所有狼众中随机选取M_num只猛狼并按照公式(9)向猎物奔袭,若途中猛狼的目标函数值Yi>Ylead,则Ylead=Yi,替代头狼并发起召唤行为;若Yi Step4按照公式(10)对参与围攻行为的狼的位置进行更新,执行围攻行为. Step5按“胜者为王”的头狼产生规则对头狼位置进行更新;按照“强者生存”的狼群更新机制进行群体更新. Step6判断是否达到优化精度要求或最大迭代次数Kmax,若达到则输出头狼位置,即所求问题的最优解,否则转step2. 为了充分测试算法的性能和特点,并与文献[3]的WPA算法进行对比,实验选取文献[3]中13个有代表性的测试函数,另外又添加了4个,共17个测试函数作为实验对象,如表1所示. 表1中特征“U”表示单峰(unimodal)函数,“M”表示多峰(multimodal)函数,“S”表示可分(separable)函数,“N”表示不可分(non-separable)函数. 单峰函数在定义域内只有全局最优值;多峰函数在定义域内有多个布局极值,用来检验算法全局收敛的能力. 表1中17个函数的变量维数从低到高排列,可以较全面地测试算法的性能. 实验用MACWPA算法、WPA算法以及经典的PSO和FSA算法分别对表1中的17个复杂函数进行重复100次寻优计算. 从平均值、最优值、最差值、标准差、迭代次数、耗时等方面对算法进行评估. 实验设置最大迭代次数Kmax=2 000,最大游走次数Tmax=20,初始狼群规模N=50,探狼比例因子α=4,更新比例因子β=6,距离判定因子ω=500.其他参数参考文献[5]设置.实验环境为Windows 8系统,2GB内存,Pentium(R) Dual-Core CPU E5800,Matlab R2010a. 表2和表3给出了4种算法对17个复杂函数寻优计算的统计结果. 当算法耗时超过2 000 s时,其结果记为“-”,不在考虑范围. 以Bridge函数为例,设定最大迭代次数为2 000,改变距离判定因子ω后分别对Bridge函数进行50次寻优计算,ω对算法性能的影响如表4所示. 以Eggcrate函数为例,设定最大迭代次数为2 000,分别测试变游走方向和固定游走方向的改进狼群算法,对Eggcrate函数进行50次寻优计算,对比结果如表5所示. 改进狼群算法收敛精度为10-7,基本狼群算法收敛精度设置为10-3. 表2给出了4种算法对6个单峰函数的计算结果. 从平均值、最优值、最差值和标准差来看,对于Easom、Maytas和Trid6三个单峰不可分函数,MACWPA和PSO算法的精度均较高,效果均明显优于WPA和FSA算法;对于Maytas、Sphere 2个单峰可分函数,维数由10维增加至30维,PSO算法的求解精度由10-37降低至10-1,而MACWPA算法的求解精度由10-7上升至10-8;对于30维的Rosenbrock 函数,MACWPA算法的求解精度较PSO算法高4个单位,可见MACWPA在处理高维函数时有一定优势.从消耗时间、达到收敛精度的迭代次数看,PSO算法耗时最短,MACWPA算法迭代次数最少,2种算法各有优势.FSA算法对全部测试函数的求解精度均较低,效果较差.对于Maytas函数、Trid6函数以及Sumsquare函数、Rosenbrock 函数,WPA算法分别在迭代800, 200,400次后速度明显减慢,达到最大迭代次数耗费时间过长,短时间内达不到收敛精度要求. 由文献[5]知,WPA算法对于单峰、不可分的低维复杂函数的寻优性能较差,改进后的MACWPA算法对这类函数的寻优性能有很大提升,算法更加稳定,表现出较高的寻优精度和较好的算法执行能力,改善了WPA算法对此类函数的寻优性能. 表1 17个标准测试函数 表2 单峰函数优化结果对比 表3 多峰函数优化结果对比 表4 距离判定因子ω对MACWPA性能的影响 表5 变游走方向h对算法性能的影响 表3给出了4种算法对11个多峰函数的计算结果.对于二维多峰函数来说,PSO算法较其他几种算法的求解精度高,而MACWPA算法也都保持了10-10的求解精度.对于Schaffer函数,MACWPA算法和PSO算法都会不同程度地陷入局部最优,但PSO算法稳定性更强,WPA和FSA算法收敛精度欠佳.对于Griewank、Rastrigin、Quadric、Ackley函数来说,当维数由30升至200时,MACWPA算法的求解精度最高,进一步说明MACWPA算法在处理高维函数时具有优势. 由表4知,距离判定因子的变化对MACWPA算法的寻优效果影响不大,6种参考数据均保持相同水平,大大提升了算法的稳定性和寻优能力.自适应步长方法一改WPA算法[5]因距离判定因子ω过大降低寻优精细度、过小使迭代次数增加降低收敛速度的缺点,使算法可根据种群当前情况自主调节步长,增加了算法的寻优精细度,加快了收敛速度. 由表5知,采用变游走方向可提高WPA和MACWPA算法的求解精度. 从耗时来看,当算法同时迭代2 000次时,所消耗的时间相差不多,亦无增加算法的复杂度;从收敛精度看,当同时达到收敛精度时,变游走方向法会大大加快收敛速度,所需的迭代次数更少,WPA算法尤其明显,避免了不必要的游走行为.从平均结果和标准差来看,变游走方向会增强算法的鲁棒性,使算法更加稳定. 为了更直观地说明MACWPA算法的优越性,图3给出了Easom、Sphere、Booth、Eggcrate及Six Hump Camel Back函数的收敛曲线图. 图3 5个函数的收敛曲线图Fig.3 Convergence curves of five functions 从图3可以看出,MACWPA算法在迭代初期,迭代结果较WPA算法更接近真实最优值;MACWPA算法通过200次迭代即可逼近最优值;其迭代过程无明显的分期变化,而WPA算法则存在明显的分期变化,在迭代中期,出现逼近真实的最优解,在迭代的初期和末期,收敛速度较慢. 总之,MACWPA算法在求解精度和收敛速度上均优于WPA算法. 在WPA算法基础上,提出了自适应步长和变游走方向的方法. 在3种智能行为中运用自适应步长,加快了算法的收敛速度,减少了参数,降低了参数对算法的影响,增强了算法的鲁棒性;变游走方向法扩大了算法的搜索范围,避免了多余的游走行为,同时提高了算法的收敛速度和搜索精度. MACWPA算法既克服了WPA算法对单峰函数优化能力差的缺点,又保持了其在处理高维函数上的优势. 参考文献(References): [1] DORIGO M, MANIEZZO V, COLORNI A. Ant system: optimization by a colony of cooperating agent[J].IEEETrans,onSystems,Man,andCybernetics, 1996, 26(1): 29-41. [2] 李晓磊,邵之江,钱积新.一种基于动物自治体的寻优模式: 鱼群算法[J].系统工程理论与实践,2002,22(11): 32-38. LI X L, SHAO Z J, QIAN J X. An optimizing method based on autonomous animals: Fish-swarm algorithm[J].SystemsEngineeringTheoryandPractice, 2002, 22(11): 32-38. [3] KRISHNAND K N, GHOSE D. Glowworm swarm optimization for simultaneous capture of multiple local optima of multimodal functions [J].SwarmIntelligence, 2009, 3(2): 87-124. [4] LIU C, YAN X, LIU C, et al. The wolf colony algorithm and its application[J].ChineseJournalofElectronics, 2011, 20(2): 212-216. [5] 吴虎胜,张凤鸣,吴庐山.一种新的群体智能算法——狼群算法[J].系统工程与电子技术,2013,35(11): 2430-2438. WU H S, ZHANG F M, WU L S. New swarm intelligence algorithm: Wolf pack algorithm [J].SystemsEngineeringandElectronics, 2013, 35(11): 2430-2438. [6] 陈斐.改进的人工鱼群算法分析与研究[D].西安: 西安电子科技大学,2012. CHEN F.AnalysisandResearchonImprovedArtificialFishSwarmAlgorithm[D]. Xi’an: Xidian University, 2012. [7] 刘彦君,江铭炎.自适应视野和步长的改进人工鱼群算法[J].计算机工程与应用,2009,45(25): 35-37. LIU Y J, JIANG M Y. Improved artificial fish swarm algorithm based on adaptive visual and step length[J].ComputerEngineeringandApplications, 2009, 45(25): 35-37. [8] 欧阳喆,周永权.自适应步长萤火虫优化算法[J].计算机应用,2011,31(7): 1804-1807. OUYANG Z, ZHOU Y Q. Self-adaptive step glowworm swarm optimization algorithm[J].JournalofComputerApplications, 2011, 31(7): 1804-1807. [9] 李开荣,陈宏建,陈崚.一种动态自适应蚁群算法[J].计算机工程与应用,2004,40(29): 149-152. LI K R, CHEN H J, CHEN L. A dynamic and adaptive ant algorithm[J].ComputerEngineeringandApplications, 2004, 40(29): 149-152. [10] 李国亮,魏振华,徐蕾.基于改进搜索策略的狼群算法[J].计算机应用,2015,35(6): 1633-1636,1687. LI G L, WEI Z H, XU L. Wolf pack algorithm based on modified search strategy[J].JournalofComputerApplications, 2015, 35(6): 1633-1636, 1687. [11] 周强,周永权.一种基于领导者策略的狼群搜索算法[J].计算机应用研究,2013,30(9): 2629-2632. ZHOU Q, ZHOU Y Q. Wolf colony search algorithm based on leader strategy[J].ApplicationResearchofComputers, 2013, 30(9): 2629-2632. [12] 薛俊杰,王瑛,李浩,等.一种狼群智能算法及收敛性分析[J].控制与决策,2016,31(12): 2131-2139. XUE J J, WANG Y, LI H, et al. A smart wolf pack algorithm and its convergence analysis [J].ControlandDecision, 2016,31(12): 2131-2139. [13] WU H, ZHANG F. A uncultivated wolf pack algorithm for high dimensional functions and its application in parameters optimization of PID controller[C]//IEEECongressonEvolutionaryComputation. Beijing: IEEE Press, 2014: 2430-2438. [14] 吴虎胜.狼群算法及其应用研究[D].西安: 空军工程大学,2014. WU H S.WolfPackAlgorithmandItsApplicationResearch[D]. Xi’an: Air Force Engineering University, 2014. [15] GUO L T, LIU S Y.An improved binary wolf pack algorithm based on adaptive step length and improved update strategy for 0-1 Knapsack problems[C]//DataScience:ThirdInternationalConferenceofPioneeringComputerScientists,EngineersandEducators. Changsha: ICPCSEE, 2017: 442-452. DOI: 10.1007/978-981-10-6388-6-37.3 仿真实验
3.1 参数设置与测试函数
3.2 实验分析

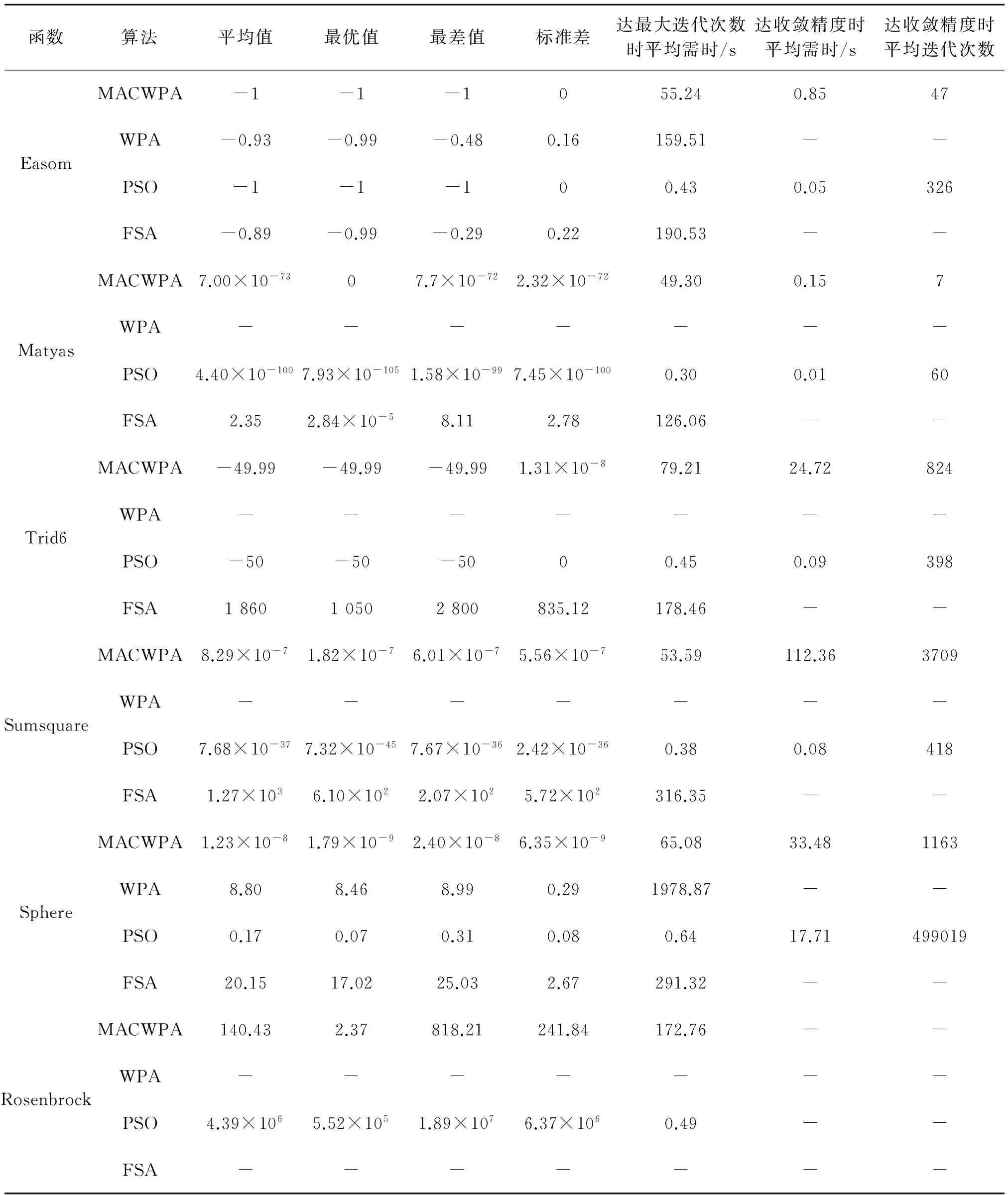
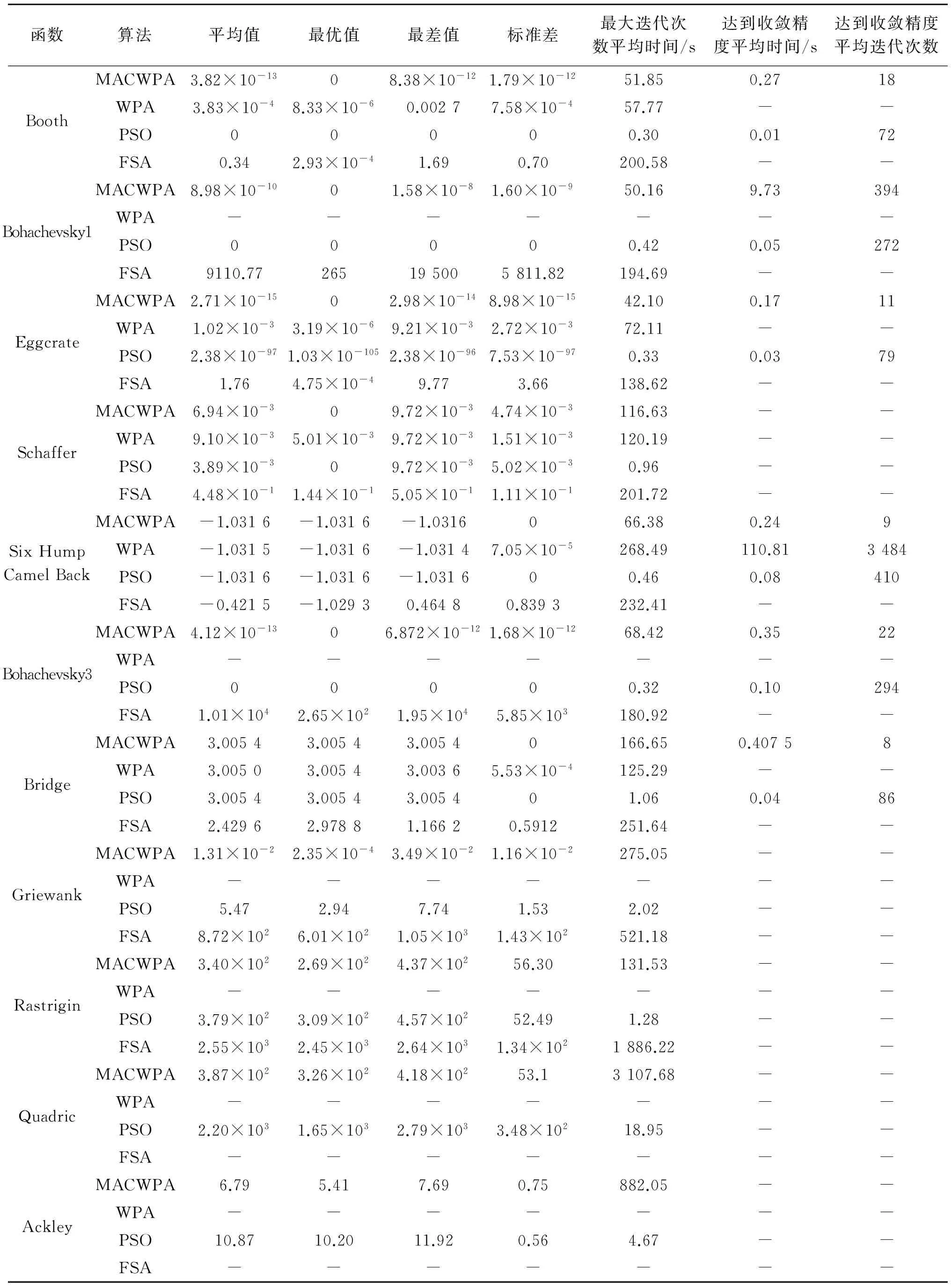
4 结 论

