基于VAR的齿轮早期故障监测研究

大 海，蔡 景，胡 维

(南京航空航天大学， 南京 211106)

1 绪论

齿轮传动因其效率高，传动比稳定以及可实现任意角度交错轴之间的传动等优点被广泛用于飞机传动系统当中[1]。在CCAR-33部第33.84条发动机超扭试验中就有发动机齿轮箱监测指标以保证飞机的适航性。因为齿轮要求很高的制造与安装精度，当齿轮发生退化时，会对飞机的适航性产生重大影响。据统计，从1970年至今，中国民航局一共颁布了47条与齿轮箱有关的适航指令。因为齿轮通常处于高负荷工况下，一旦发生故障可能会造成重大事故，因此通过先进的监测技术提前发现早期故障，可以有效避免重大事故发生。而且对减少故障停机时间，保障飞机的适航性有着重大意义[2]。

状态监测与故障诊断技术能明显提高齿轮传动系统的可靠性，减少故障的发生。齿轮箱是一个封闭系统，工作时其故障特征很难直接观察到。一般传统方法是按照齿轮箱温度[3]，滑油[4]，噪音[5]，振动[6]等经验数据判断齿轮箱是否有故障存在。

在最近的学术研究成果中，先进的非参数方法被广泛应用于齿轮箱早期故障诊断，如小波分析技术、短时傅里叶变换和多分辨率傅里叶变换等。一些学者将参数化的时间序列模型应用于齿轮箱故障检测中，这些模型基于以下原理：随时间采集的振动数据点有一个内部结构，如相关、自相关、趋势或者季节性波动。其中加速度传感器获得的齿轮箱振动数据作为状态监测的参数对齿轮早期故障诊断作用比较明显，因此渐渐发展为主流的状态监测与故障诊断方法。但这些方法由于环境噪声等因素存在往往精度不高。

利用齿轮在健康或者异常状态下这些参数的差异性来判断齿轮是否处于健康运行状态是目前的一种主要思路，关键问题是如何选取参数。为此，本文采用VAR模型，得到齿轮箱振动幅值残差，将残差的变化作为判断齿轮是否存在早期故障的指标。

2 时域同步平均方法

齿轮状态监测振动信号主要由齿轮啮合信号，故障冲击信号以及背景噪音信号三部分组成。为了精确地掌握齿轮的运行状态，必须把背景噪音信号消除。时域同步平均算法是常用的从齿轮振动信号中消除背景噪音信号的方法[7]。其原理图如图1。

在齿轮状态监测过程中，由于采样频率限制，每次采样的数据包含了齿轮的多组振动信息，这些信息中有大量的背景噪音。根据噪音的均值为0的特点，将一次采样的数据按照齿轮旋转一周为一段进行划分，然后将每一段数据对应相加，取平均值。因此在每个采样点中的背景噪音信息因为多次相加，取平均值，慢慢趋近于零，但是齿轮本身的啮合以及故障冲击信号因为均值不为零，在多次相加平均后慢慢突显出来。

一般来说，在做时域同步平均时，因为要求每个周期内加速度计采样点数一致，所以要求齿轮转速不变。但是在实际情况中很难做到，齿轮转速一般在标准转速范围内波动。所以通常在监测赤露振动加速度信息的同时，需要一个转速同步脉冲信号触发加速度计的A/D转换器。这样就可以保证每次加速度计测得的齿轮箱振动信号与转速同步，把振动信号当作恒定转速处理。

齿轮每旋转一圈采样点数为：

⎤

(1)

式中，「·⎤为向上取整，n为待诊断齿轮每分钟转速，fs为所用到的加速度计采样频率。

本文所用试验数据来源于宾夕法尼亚大学90年代一系列变速箱状态监测实验中的常工况定轴变速箱状态检测试验，试验台如图2所示。

齿轮箱的主动轮轮齿为30，从动轮轮齿为46且都为斜齿轮。状态监测传动参数包含振动参数，噪音参数，转速参数，扭矩参数等。齿轮箱参数如表1所示。

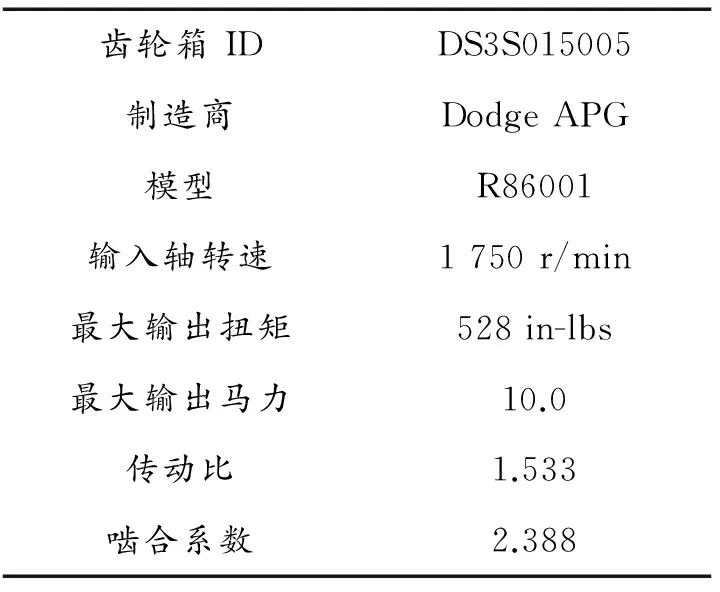
表1 齿轮箱参数

为了缩短实验时间，试验分为两个阶段进行。第一阶段，转速为1 750 r/min，扭矩为540 lbs，运行96小时后检查，齿轮箱工作正常。第二阶段，转速为1 750 r/min，扭矩为 1 620 lbs，运行直至齿轮箱失效。试验中第一阶段采样间隔为8 h，采样频率为20 kHz，采样时间为10 s，数据量为 200 000个数据点。试验中第二阶段采样间隔30 min，采样频率与采样时间与第一阶段相同。采样所用到的加速度传感器AD转换器的分辨率为16位，足够保证实验所需精度。实验原始数据记录如图3所示。

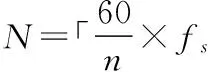
选取两倍TSA长度进行处理，即每段数据为2104个点，如图4所示。

将实验数据前后对比可知，时域同步平均方法能很好去除振动信号中的噪音部分，将啮合信号以及冲击信号较为真实体现。

3 向量自回归(VAR)模型建立

原始振动幅值数据经过TSA过程后得到各个采样时间段降噪之后的振动幅值信号。根据齿轮在健康状态下与异常状态下的不同TSA数据特征，将第一次采样的TSA数据作为训练数据，得出向量自回归(VAR)模型。然后以此模型为预测模型确定整体数据的残差。这样健康部分的数据仅表示预测误差，若有故障产生，那么残差不仅包含了预测误差，还包含故障带入的振动信号所引起的误差。

从图5可以看出单位根全部落在单位圆中，健康数据部分服从一个平稳的VAR过程：

(2)

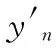
针对二维VAR过程，可用下式表示：

(3)

Reinse[8]表明系数Φr与εn可由最小二乘估计获得。

常用的确定模型参数p的方法有多种，本文选用AIC原则确定模型的阶数。AIC值计算方法见下式：

(4)

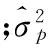
表1 VAR模型部分参数值

4 基于VAR残差的故障监测

确定模型的参数后，得到模型预测值，将预测值与实际值相减，即为TSA信号的残差，如下式所示：

(5)

对于VAR模型，首先要模型阶数P能使模型AIC值最小，其次是模型拟合得到的残差相关性[9]要小，这就表明模型拟合程度高。从图6可以看出，89阶的VAR模型残差相关性很小，所以建立的VAR模型是适用的。

将健康部分数据建立的VAR模型应用于整个试验过程采集到的数据上，得到整个试验过程残差数据，如图7。

从图7可以看出，健康部分数据残差平稳。从第40次采样开始，残差有峰值产生，初步判定齿轮有微裂纹产生，从第40次到第70次为裂纹产生到扩展的过程。最后一次残差峰值非常密集，可能发生断齿。因此，将齿轮箱原始信号经过TSA处理后，利用VAR模型提取出残差。图8为每次取样的残差标准差变化图。

因为每次采样的时间间隔为半小时，因此，从图8可以看出，当工作到第35 h左右，用VAR模型得到的残差值发生了明显的变化，说明出现故障。这也符合实际情况，因齿轮箱在第35.8 h，进行开箱检查，发现从动轮有两个完全断掉的齿，如图9所示。这说明采用本方法的准确性。

如采用基于振幅变化判断故障的传统方法，由于环境的干扰，难以发现早期故障，如图10所示。从图10可以看出，系统在试验中后期，整体残差值慢慢增大且有峰值出现。残差结果不仅包含了预测误差，还有故障信号误差。

与传统方法相比，本文提出的基于向量自回归模型的残差值方法，能更早、更显著识别出齿轮的早期故障。说明了本方法有效。

5 结论

1) 本文提出基于向量自回归模型的残差值方法：消除齿轮状态监测振动信号的背景噪音，利用齿轮健康时段的振动监测数据，建立VAR模型，得到残差值。

2) 本文通过残差值的高低判断故障是否发生，并通过与实际情况和传统方法进行比较，说明了所提方法准确、有效。

参考文献：

[1] 王德伦,马雅丽.机械设计[M].北京：机械工业出版社,2015.

[2] 倪侃.随机疲劳累积损伤理论研究进展[J].力学进展,1999，29(1)：43-65.

[3] 郭鹏,DAVID INFIELD,杨锡运.风电机组齿轮箱温度趋势状态监测及分析方法[J].中国电机工程学报,2011,31(32):129-136.

[4] 李鑫,左洪福,蔡景.齿轮箱滑油系统静电监测[J].交通运输工程学报,2016,16(2):72-81.

[5] 陶发荀.齿轮传动噪音及故障分析诊断[J].汽车零部件,2010(7):37-40.

[6] ZHU Z K,YAN R,LUO L,et al,Detection of signal transients based on wavelet and statistics for machine fault diagnosis[J].Mechanical Systems and Signal Processing,2009,23(4):1076-1097.

[7] 罗德扬.时域同步平均原理与应用[J].振动、测试与诊断,1999(3):202-207.

[8] REINSEL G C.Elements of multivariate time series analysis[M].New York:Springer,1997.

[9] 潘省初 周凌瑶.计量经济分析软件:EViews SAS快速上机指南[M].北京： 中国人民大学出版社,2005.