焊接钢质药筒力学特性分析研究

杨吉林，田晓丽，乔茹斐，白敦卓，仇东旭

(1.中北大学 机电工程学院， 太原 030051； 2.豫西工业集团， 河南 南阳 473000；3.山东特种工业集团， 山东 淄博 255201)

弹丸发射时发射药产生的火药气体压力直接作用在药筒上，迫使药筒发生弹、塑性变形；当压力下降时，随着炮膛的弹性恢复，会给药筒施加反向压力，影响药筒的退壳。因此，研究药筒在不同发射阶段的力学特性有着重要的意义。由于许多学者致力于药筒的研究，近年来从黄铜药筒、焊接钢质药筒到铝合金药筒，从可燃药筒到塑料药筒[1-4]，药筒的材料和性能均得到大幅度提升。此外，郭振宇[5]从药筒发射过程中的惯性力着手，推出药筒运动的微分方程；田晓丽等[6]研制了专用的药筒有限元分析前处理软件系统；卫丰等[7]利用有限元软件模拟了药筒的发射应力和抽壳力。

本文以焊接药筒为例，对药筒在发射过程中各部分的应力、应变进行分析求解，得到其变化规律，计算其抽壳力。再通过LS-DYNA软件对此过程进行数值仿真，将仿真结果与理论计算结果进行比较，验证其正确性，对药筒研究有重要指导意义。

1 模型简化

一般药筒底端均有封口，但在弹丸发射过程中这一端被闩体挡住,使药筒沿轴向位移很小，应变沿轴向为零。对筒体而言，由于药筒与炮膛的长度均远大于其外径，从构件的几何形状和受力特点，可将问题简化为平面应力问题。而由于药筒内的应力分布对称于药筒的中心轴线，所以它又是一个轴对称问题。

基于分析问题的特点，建立极坐标系统(径向为r，轴向为z并与药筒中心轴重合)，如图1。在该坐标系统中，横截面内的位移分量均对称于坐标原点分布，其径向位移u和环向位移w均与θ无关[8]：

其中，r1、r2为药筒内、外半径，R1、R2为炮膛内、外半径，药筒与炮膛初始间隙为U0，药筒内壁受到膛压P的作用。

2 筒体力学特性分析

弹丸发射时，根据火药气体压力的变化和药筒变形特点，可以将药筒和炮膛的受力变形状态分为三个阶段：贴膛前变形阶段，贴膛后变形阶段和卸载阶段。贴膛前，随着膛压的升高，药筒发生弹性变形，当膛压大于屈服极限后，药筒发生塑性变形；贴膛后，药筒继续塑性变形，而炮膛在膛压和药筒作用下发生弹性变形。当弹丸抛出后，药筒和炮膛同时进入卸载阶段。如图2是弹丸发射时，膛压随时间的变化曲线。

2.1 贴膛前变形阶段

设贴膛前膛压为P1，0≤P1≤Pt，Pt为贴膛时膛压。

在这个阶段，根据薄壁圆筒理论，可知药筒的径向应力、环向应力、轴向应力分别为：

(1)

根据广义胡克定律可知：

(2)

药筒的径向弹性位移为：

(3)

其极限径向弹性位移为：

(4)

其中:tb=r2-r1是药筒的壁厚，σs为药筒屈服应力,E1为药筒弹性模量。

2.2 贴膛后变形阶段

设贴膛后膛压为P2,Pt≤P2≤Pm，Pm为最大膛压。

药筒紧贴炮膛后，在膛压的作用在炮膛发生弹性变形。根据厚壁圆筒理论，可知炮膛的径向应力、环向应力、轴向应力分别为：

(5)

炮膛的径向位移为：

(6)

其中:E2为炮膛的弹性模量，μ2为炮膛的泊松比。

贴膛后炮膛发生弹性变形，不应该发生塑性变形，则极限膛压为:

(7)

炮膛的最大径向位移为:

(8)

药筒紧贴炮膛后，随着炮膛一起变形。药筒最大径向位移Um=U0+Ut。

药筒的环向应变为：

(9)

应变可以分解为弹性应变和塑性应变。即εφ=εφc+εφp。根据式(2)可得弹性应变，进而求得塑性应变。

2.3 卸载阶段

设卸载膛压为P3。

在膛压降到大气压的过程中，药筒与炮膛产生弹性收缩。由于材料性能和加工硬化的影响，炮膛可以逐步恢复到变形以前的状态，而药筒不能完全恢复到变形以前的状态，保持一定的变形量ΔU。若ΔU≤U0,药筒可直接退壳；反之，药筒与炮膛之间会发生过盈，相互挤压，产生接触压力，需要一定的抽壳力才能完成抽壳。炮膛的弹性位移为Ur=Ut-U1，可通过式(6)反求出药筒与炮膛之间的压力，为：

(10)

2.4 抽壳力的计算

对于整体式药筒，由于斜肩部的过渡，使得筒体与筒口半径相差较大，为计算方便，将药筒分为两个区域，即一区和二区，如图3。

抽壳力F=F1+F2

Fi=2πfiliRiPg,i=1,2

(11)

其中:fi为第i区药筒与炮膛间的动摩察因数，li为第i区药筒与炮膛的接触长度，Ri为第i区药筒与炮膛的作用半径，Pg为药筒与炮膛接触压力，为：

(12)

3 筒底变形分析

3.1 不贴膛段

在药筒变形过程中筒底有一特殊段始终无法贴膛，这使得药筒根壁起始处与筒底受到很大的剪力作用，并使贴膛临界处膛壁产生局部弹性变形，相应地产生很大的集中反力，该集中反力对筒底产生相应的弯矩。此时，药筒根部不贴膛段的受力变形与弹性基础梁的弯曲相似，该梁的微分方程和挠度方程为：

(13)

(14)

根据文献[8]，可得挠度方程解为：

(15)

挠度y是一条迅速衰减的波状曲线，该特殊段的弯曲变形也是一波状曲线。挠度方程二阶导数为：

(16)

任意截面的弯矩为：

(17)

最大弯矩发生在βx=π/2截面，x=π/2β；最大弯曲应力σmax=Mmax/W，W=t2/6，是筒底这一段的抗弯截面模量。

3.2 药筒最底端

药筒最底端一直受到火药气体的压力，使其向外运动。药筒底端中心面是一个受内压的压盖。

在底端中心面处：

σz=P

σr=σφ=0

(18)

其对应的应变为：

(19)

在药筒底部边缘处由于圆弧段受压，使其一直受到弯矩作用。随着药筒口部及体部与炮膛紧贴，药筒底部不断振动。

4 仿真分析

4.1 模型的建立

建立焊接药筒的几何模型时，为了节省计算时间，根据药筒结构的对称性和弹丸发射过程中膛压作用的对称性，文中将分析模型简化为二维平面对称模型。按照焊接药筒的设计理论，把药筒分为六个区，分别为筒底部、筒底环、药筒缘焊缝、药筒环、药筒体部和药筒口部。药筒和身管的几何模型如图4。

4.2 主要材料及状态方程

设药筒为理想弹塑性材料，本模拟中采用(PLASTIC_KINEMATIC)状态方程。将身管45号钢看成弹性材料，本文采用(ELASTIC)状态方程。具体材料参数见表1。

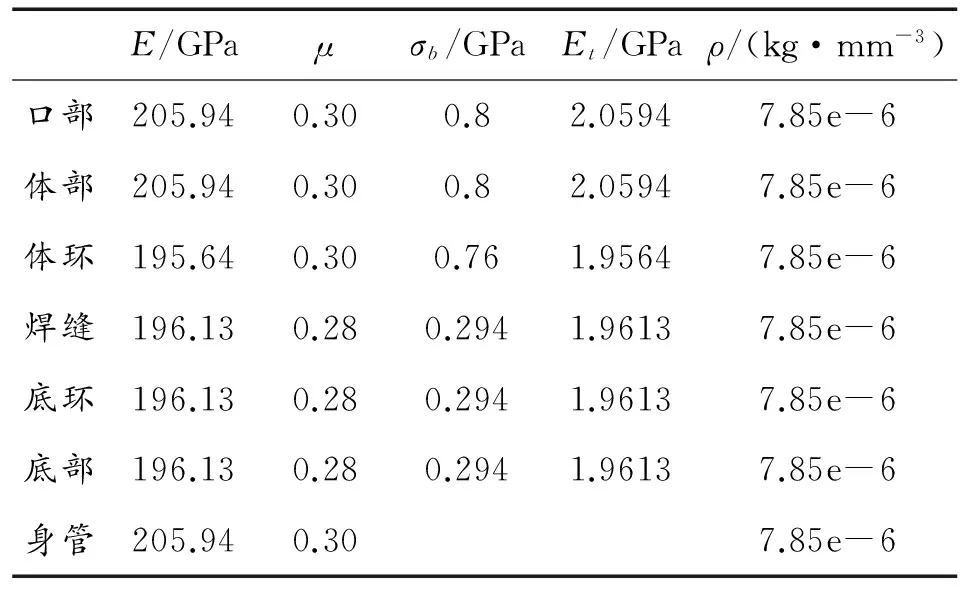
表1 材料参数

4.3 仿真结果

1) 通过使用LS-DYNA后处理器观察药筒在不同时刻的变形，得到不同时刻的局部应力云图，如图5。

2) 对药筒体部和炮膛各取一单元进行分析，其具体尺寸为：r1=77.3 mm，r2=79.5 mm，R1=80.052 mm，R2=139.47 mm，U0=0.552 mm，将仿真计算值与理论计算值进行对比，如图6。

贴膛时膛压为0.039 MPa，由式(4)计算得极限径向弹性位移为0.005 14 mm，小于初始间隙。贴膛时药筒已经发生塑性变形。由式(8)计算得贴膛后炮膛的最大弹性位移为0.311 mm。

3) 从仿真结果中取药筒底部环形焊缝处单元和最底端单元，得到其应力变化曲线，如图7和图8所示。

由于有不贴膛段存在，环形焊缝处一直有应力集中，所以应力较大，可能导致药筒断裂。

4) 绘制抽壳时刻药筒各单元残余应力分布图，如图9。由式(11)计算得抽壳力为4.237 kN。

5 结论

1) 由于膛压作用，药筒沿轴向抖动，造成轴向应力有小幅度波动。

2) 药筒贴膛后，与炮膛组合成厚壁圆筒，造成仿真结果与实际测量值有误差，在膛压最大时误差最大。

3) 药筒贴膛后，药筒底部向后运动被闩体挡住，使筒底不贴膛段形成悬臂梁，不断振动。

4) 药筒底部环形焊缝处应力最大。在生产实践中应该注意环形焊缝的焊接速度。

5) 不同的抽壳时刻，药筒的变形和受压状态不同，所以抽壳力的大小与抽壳时刻有重要关系，即药筒的受力和变形均会影响到药筒的退壳。

参考文献：

[1] 何清.焊接钢质药筒设计理论与研究[D].太原:中北大学,2005.

[2] 尹兆杰.药筒CAE理论与技术研究[D].太原:中北大学,2007.

[3] ROBBINS F W,COLBURN J W,ZOLTANI C K.Combustible Cartridge Cases:Current Status and Future Prospects[J].Combustible Cartridge Cases Current Status & Future Prospects,1992.

[4] 李华.工程塑料在弹药部件上的应用及发展趋势[J].工程塑料应用,2007,35(8):70-72.

[5] 郭振宇.火炮药筒在发射状态下的工作过程及其基本参量[J].兵工学报,1981,2(3):34-39.

[6] 田晓丽,杨黎明,何清,等.药筒有限元分析前处理软件系统研究与应用[J].应用基础与工程科学学报,2009,17(4):636-642.

[7] 卫丰,张光.药筒发射应力和抽壳力的有限元分析[J].爆炸与冲击,2001,21(1):72-75.

[8] 卓卫东.应用弹塑性力学[M].2版.北京:科学出版社,2013.

[9] 陶春达,战人瑞.冲击内压作用下厚壁圆筒弹性动力分析[J].西南石油大学学报：自然科学版，2000,22(2):77-79.

[10] 谈乐斌,蔡糅,袁人枢.厚壁圆筒动态强度的有限元分析和实验研究[J].弹道学报,2010,22(4):86-88.

[11] 李敏,刘百慧,马秋生.承压薄壁容器应力分析的讨论[J].力学与实践.2011,33(2):82-84.

[12] 张相炎,郑建国,袁人枢.火炮设计理论[M].北京：北京理工大学出版社,2014.