贝叶斯网络的分层推理算法

李振明 柴冰

摘要：贝叶斯网络算法是基于事件发生的一种概率信度计算。为了准确判断各个事件发生的概率，提高判断的精度与准确度，提出了一种贝叶斯网络的分层推理算法。这种方法将贝叶斯网络进行结构化处理，对于节点集进行分析，更精准的去推测事件的概率。分层推理是在贝叶斯网络的基础上，结合贝叶斯网络的推理算法提出算法的基本思想，再在理论上进行推理验证，最后进行仿真试验验证该算法的准确性与可实施性。

关键词：贝叶斯网络；信息分类；分层推理

中图分类号：TP393 文献标识码：A 文章编号：1009-3044（2018）08-0164-05

1引言

贝叶斯网络是一种研究不确定性问题的重要的方法之一，贝叶斯网络技术依赖于概率和统计的理论，掌握贝叶斯网络技术需要有坚实的数学基础。它具有自然的表达方式以及强大的推理能力还有灵活的决策机制等优点。本文在贝叶斯网络的基础理论的框架之上研究贝叶斯网络的分层推理，并将贝叶斯网络信息层次结构化处理，能够更灵活地去处理信息，使得得到的结果更加准确和具有实用性。

同时随着互联网的应用的不断推广，大量的信息可以很容易的获得，利弊相依，在获得大量数据的同时对应于数据的处理分析与应用也有着很多的困难，如何去准确地把握数据是一件值得挑战的事情。最常用的手段就是把不同的信息文本进行分类，再获取信息的时候就可以在与其相对应的类别中去查找特定的信息。这样不仅可以提高获得结果的速率，也可以保证结果的准确性。由于数据网的庞大与相关联性，所以层次结构分析是不可以去忽略的。

贝叶斯方法对于信息的挖掘有着很灵活的应用，已经有很多的学者在研究这一贝叶斯网络的信息分类以及应用的问题。在实践中已经有很多种的方法在研究，处理有着大量的类别的信息，但是这些算法在样本数据较少的情况的时候效果又不太明显。本文主要是基于信息主题，提出的一种高效的贝叶斯网络分层推理的算法：算法主要是通过信息的相关性来强化关键词的作用，将贝叶斯分类器的精度提高，从而提高所得结果的准确性。即使在获取的信息样本数比较少的情况之下，也可以获得比较实用的分类精度。在推理算法研究方面，对静态贝叶斯网络推理研究得比较多，成果也比较多，主要有消息传递算法、条件算法、连接树算法、符号概率推理算法、弧反向，节点缩减算法、随机抽样算法等。

2贝叶斯网络分层推理算法

2.1模型建立

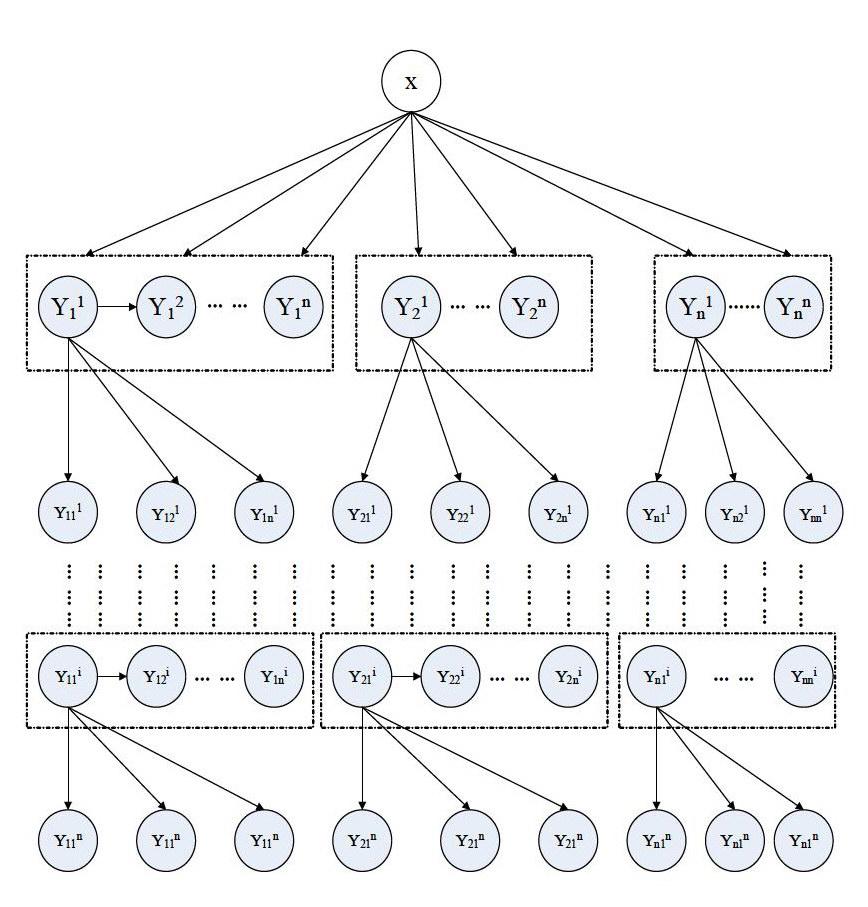
分层推理的结构图如上图所示。x为隐藏节点，Y11n-Yn1n为观测节点Y11n-1-Yn-11n-1为观测节点的隐节点。根据贝叶斯算法，与所得到的先验条件求出隐节点的概率，将所得的结果作为观测数据，对上一层次进行推理，缩小模型结构，最终的出隐节点X的概率。

对于单个节点的模型，每个结点的变量都有很多观测节点，根据所观测的节点概率以及条件概率去计算它的后验最大概率。

2.2基本思想

在研究对象发生故障之后，根据获得的证据信息和所有的先验概率推理得到第一个层次的精确推理结果最后得到发生故障的类型。然后根据所得到的结果的层次分类中进行计算。把第一次推算出来的结果作为证据信息再根据已知先验概率推理精确的数据最终得到所研究对象故障类型的真正原因。

2.3算法描述

贝叶斯网络分层推理的算法推理的过程主要分为三步骤进行：第一步，对研究的事件发生可能性进行层次分类，不同的事件可根据不同的原则进行分类，才可以进行层次化研究，不断地缩小事件发生因素的范围。第二步，通过第一步的层次划分之后，根据所持有的证据信息以及先验概率进行精确的概率推算，利用贝叶斯网络推理算法，得出事件发生因素的后验概率，从而缩小了研究的范围，使得最终得出的结果更为精确。第三步，就是把第二步所得出的结果作为证据信息然后根据引起这个证据信息发生因素的先验概率进行推算，得出更为准确的结果，分析出故障发生的因素。如果层次的分类更加细致的化，只需要重复步骤，不断地去细化研究。

分层推理就是先把事件发生的因素范围缩小这样更方便去研究去总结，能够更加准确无误的找出事件发生的原因。把得到的数据带人到下一个层次的计算，这样就可以计算出这个事件发生的主要因素，这也是对确定性证据的一种研究，如果层次比较多，需要不断迭代计算，去缩小事件发生的范围，层次越多越为复杂，但是相对于其他的算法而言，能够提高效率以及准确性。

2.4贝叶斯网络分层推理的计算步骤

对于证据的处理，必须考虑其子节点Z与父节点X的影响。对于子节点与父节点信息的传递必须要以不同的方式。假设节点Y具有变量（Y1，Y2，…，Yn），父節点为A，B，子节点为C，D。